基于边缘计算的多授权属性加密方案
2023-09-13程小辉丁黄婧
程小辉,丁黄婧,邓 昀,王 宇+
(1.桂林理工大学 信息科学与工程学院,广西 桂林 541006;2.桂林理工大学 广西嵌入式技术与智能系统重点实验室,广西 桂林 541006)
0 引 言
现有的属性加密一般为单一授权机构,具有巨大的安全隐患,若受到攻击则无法保障整个系统范围内用户数据安全,而多属性授权加密能够分散管理属性从而提高系统安全性[1-4]。Kai Zhang等[5]通过可追溯性的多权威CP-ABE方案实现用户跟踪性与细粒度访问控制的实用加密。Odelu等[6]通过椭圆曲线在计算开销上的优势提出由此代替用户解密时的双线性计算[7]。Ting Liu等[8]提出外在云环境下支持黑盒跟踪的多权威CP-ABE加密。同时将解密外包至边缘节点,将边缘节点属性加密相结合,能够极大程度缓解数据通信与数据安全所带来的额外计算开销,并减少运行时间,从而提高数据信息在方案中传递的效率。基于此本文提出了基于边缘计算的多授权属性加密机制研究,边缘节点承担大部分的运算开销,多授权中心分摊属性管理,直接减少单授权机构的秘钥托管与局部失控问题[9]。
1 预备知识
1.1 访问结构
数据拥有者需要设置一个门阀值,假设访问控制集合与用户属性集合相交数量大于设置门阀值,则用户成功获得用户私钥并解密。设U={u1,u2,u3,u4,u5} 是访问属性集合,同时设置门阀值为k=3, 两者构成一个访问结构[10],其中u1,…,u5为不同属性的值。若存在A={u1,u2,u4,u6,u7} 与B={u1,u5,u6,u7},A∩U个数大等于门阀值k,B∩U个数则不满足。则称A中包含的集合称为授权集合,而B称为非授权集合。
1.2 线性秘密共享方案
线性秘密共享方案(linear secret sharing scheme,LSSS)[11],假设一个基于用户集合P关于秘密分享的方案α在P上看是线性,则α必然满足下述条件:
(2)存在由秘密共享方案α生成的m×n的共享矩阵M, 对于i=1,2,…,m, 该矩阵的第i行Mi都被一个相应用户ρ(i) 标识,其中ρ是一个从 {1,2,…,m} 到P的映射函数。给定一个随机列向量v=(s,v2,v3,…,vn)T, 其中s∈P是共享秘密值,而v2,v3,…,vn则由随机数生成。 (M·v) 表示根据共享方案α将秘密值s分享t份,λi=(M·v)i则是表示属于用户ρ(i) 的属性。

1.3 椭圆曲线密码体制
椭圆曲线密码体制(elliptic curve cryptosystem,ECC)[12]的安全性主要由椭圆曲线离散对数问题(ECDLP)[13]的困难性来实现。ECC作为公钥密码体制[14]中的一个大类,相较于其它同类加密算法,其系统参数值与密钥长度决定了其存储开销与计算开销上更具优势。ECC因其算法公式与数学中的椭圆周长公式相似而得名,所得曲线的变量与系数都在有限域p(有限域的阶数为p)[15]上,由二元三次方程表示为:y2=x3+ax+b, 记为Ep(a,b)。 是由曲线方程全体解 (x,y) 加上一个无穷远点O构成的集合,其中x,y∈Zp且均为未知数,a,b是系数同时满足4a3+27b2≠0。 ECC计算规则具体如下述:
(1)所有在椭圆曲线上的点Q,都满足Q+O=Q-O=Q。
(2)所有在椭圆曲线上的点U(x1,y1) 与其对称点V(x1,-y1), 都满足U+V=O, 且此时对称点V(x1,-y1) 为U(x1,y1) 的负元。
(3)若点A(x1,y2) 与点B(x2,y2) 均在椭圆曲线上,且满足A≠-B, 则R=A+B=(x3,y3)。 其中
x3=Δ2-x1-x2,y3=Δ(x1,x3)-y1
(1)
Δ={y2-y1x2-x1(modp),x1≠x2
3x21+u2y1(modp),x1=x2
(2)
假设数据使用者A与数据拥有者B的交互由ECC为基础,则需要先将信息数据映射至椭圆曲线Ep(a,b) 上的某点G, 并将其作为基点。具体通信过程如下述:
(1)A选择生成一个私钥k,并生成公钥K=kG;
(2)A将K,G与Ep(a,b) 发送给B;
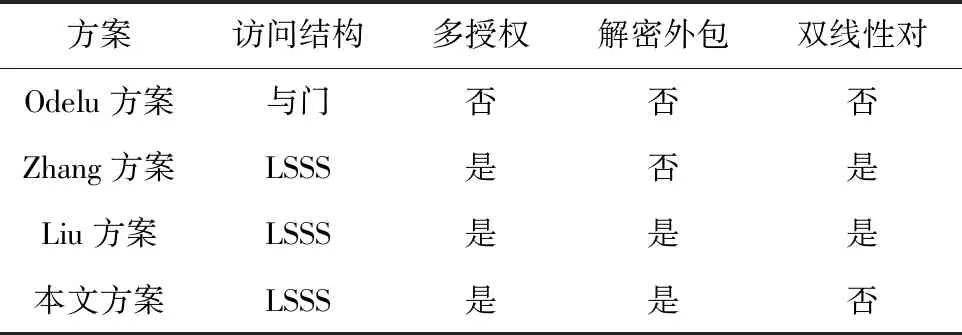
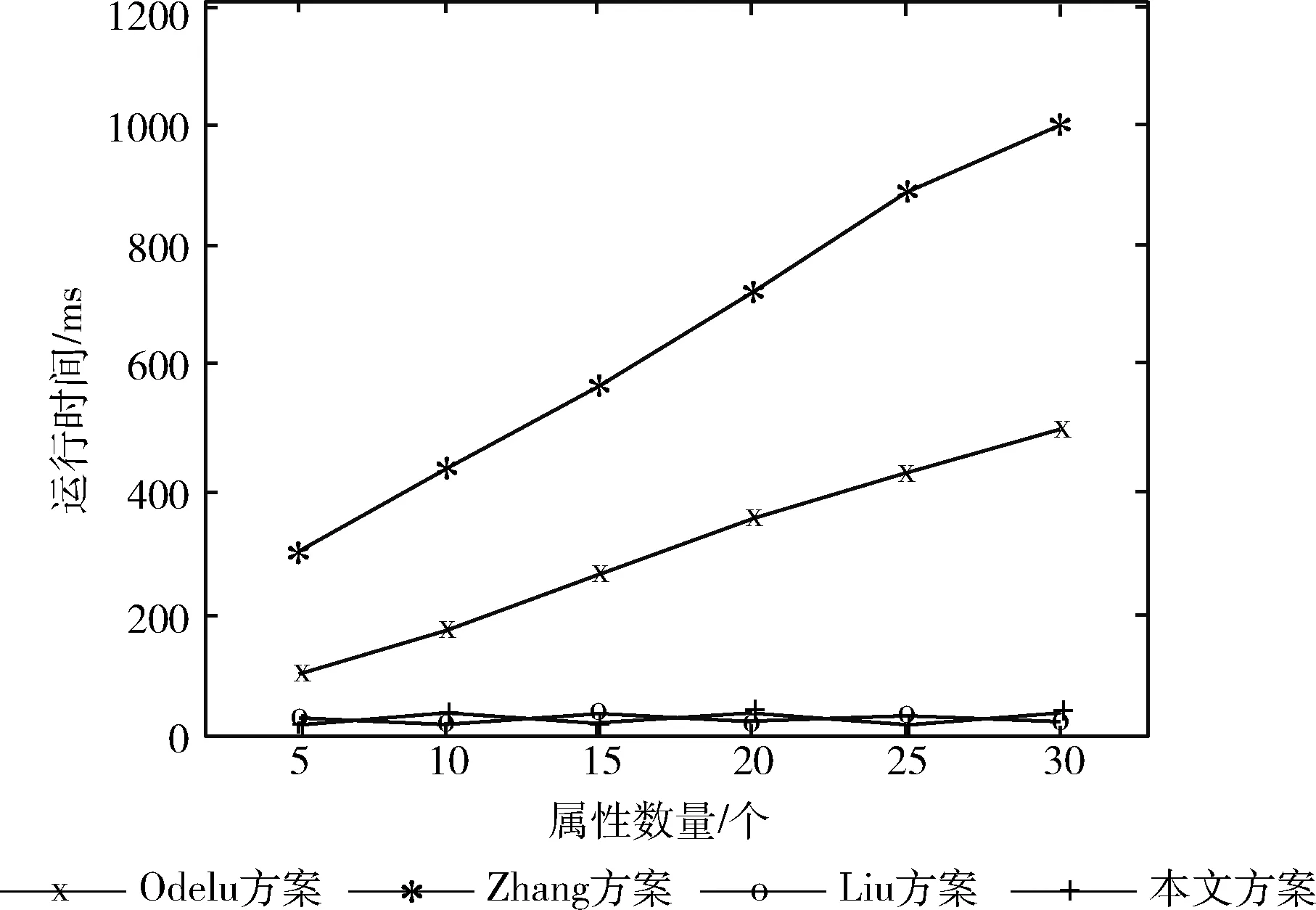
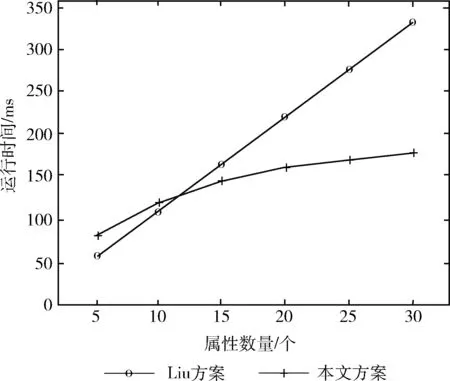
(3)B收到后将明文数据编码至Ep(a,b) 上任意一点M, 并产生随机整数r(r (4)B计算生成密文点C(C1,C2), 其中C1=rG与C2=M+rK, 并发送至A; (5)A收到后计算C2-kC1, 得出结果正好为点M, A对点M进行解码获得明文数据。 本文提出了一种应用在边缘环境下的多授权属性加密方案,系统模型如图1所示。方案为三层主结构,分别是云服务层、边缘层与用户层。云服务层包含云服务器(cloud server provider,CSP)与中央授权机构(central authority,CA),作为整个方案的核心运行层,云服务层负责整个方案的大部分数据存储与数据持久化。通过对CA生成的参数与CSP的数据进行认证与分发,来推动系统访问控制方案工作的完成。边缘层由众多来自不同域的边缘节点(edge node,EN)、属性授权机构(attribute authority,AA)与调度服务器(dispatch server,DS)构成,方案通过这些EN来完成对数据的部分传输与解密外包工作,将解密的认证过程外包至EN中来达到减少终端用户运算开销,降低云服务层被攻击情况可能性的目的。并且通过EN减少用户在传统访问控制下需要将明文数据与CSP直接进行互动的时间开销,达到提高访问方案整体效率的目的。DS完成系统的负载均衡工作,保证不因数据堵塞或数据等待过度带来多余的网络时延并保障系统稳定性。同时每个AA分管不同属性,AA之间属性集两两互不相交,减少了单点失效或单点攻击给系统整体带来的威胁。用户层包括数据拥有者(data owner,DO)与数据使用者(data user,DU),数据的产生、上传与申请、下载主要发生在用户层。 图1 系统模型 如图1所示,该模型主要有6类实体参与方,分别为中央授权机构CA、云服务提供商CSP、属性授权机构AA、边缘节点EN、数据所有者DO和数据用户DU。 CA作为访问控制方案参与方,属于无条件被信任的机构,负责方案中设备与平台的注册,产生与分发系统的安全参数k与全局参数PP。 CSP是属于云端的服务器,用户上传与下载的数据均来自于此,它具有巨大的数据存储空间。DO将数据密文与密钥密文上传至EN或CSP,对密文进行持久化保留,同时对EN的请求无条件执行。 AA是完全可信机构,不同AA两两之间所管理的属性集合均不相交,主要用于DO的注册与为其生成绑定唯一用户标识UID的私钥,以及维护自身的属性列表。 DS作为完全可信机构负责系统中用户数据流的资源分配与均衡工作。用户上传、下载数据请求时先对DS询问自身第一区域内EN的负载状况,判断是否处在负载饱和状态,若未饱和则DS发送肯定反馈,用户发送上传信息或下载请求至域内EN进行一步处理。若负载状况饱和,则由DS综合系统资源池中EN的域内节点数量及信息,反馈具有服务能力的邻近EN节点标识至用户。 EN在本质上与CSP一样,都具备网络数据存储与传输处理的功能。区别在于EN比CSP更接近用户,比CSP分布更加分散,更利于快速与终端设备产生联系。作为CSP与用户之间的中间节点,EN负责预处理和验证数据。同时,加密数据短时间存储在其中,并上传CSP。当DU向AA提出资源请求,EN则将密文数据预解密后发送至相应DU。EN所具有的相对低时延与高稳定性是EN的本质优势,通过EN自身更高的存储能力与物理性能,代替用户进行部分存储与本地计算操作,能够降低系统网络的通信压力,保障系统的稳定性。 DO作为密文的生成者与上传者,由其对数据明文进行对称加密后,再对密钥与密文加密生成最终密文CT, 将密文CT上传。 DU向拥有自身属性集的AA发送自身属性集C,以便AA对访问控制策略与属性集进行认证与反馈。其次通过EN预解密后的密文CT′进行解密后取得明文数据M。 本文系统通过EN外包解密操作的同时,仍然需要考虑数据不在本地操作所带来的时延问题。尽管直接在数据本地源处理计算操作能够最大程度减少响应时延并使系统稳定性达到最优,但不得不考虑本地用户功耗以及计算性能上的短板,这可能给系统带来更大的开销,因此EN作为最靠近本地用户的域内节点,需要寻求不可避免的传输时延与计算开销上的高性比平衡点。同时,当EN在本地充当存储与交互的角色后,需要CSP发送或接收的数据需求变少,系统的交互延迟自然能够降低,系统稳定性也能得到保证。 本文系统模型主要有由4部分算法构成,分别为系统初始化(Setup)、数据加密(Encrypt)、密钥生成(KeyGen)、数据解密(Decrypt)[16]。 (1)系统初始化算法包括2个子算法:全局初始化算法CA.Setup与属性机构算法AA.Setup。 CA.Setup(k)→(PP)。 中央授权机构在初始化阶段设置安全参数k, 以此输出系统全局参数PP并向全系统公开此参数。 AA.Setup(PP)→(MK,PK)。 各个属性授权机构根据全局参数PP构造专属主密钥MK与公钥PK, 其中公钥向全系统公开。 (2)数据加密算法 Encrypt(PP,PK,(A,ρ),M)→(CT)。 DO首先使用对称加密对明文进行初步加密,接着定义LSSS访问结构 (A,ρ) 作为输入,其中A为根据DO访问策略T生成的共享矩阵,而ρ分别对应矩阵A中属性的行数。同时输入全局参数PP、 属性公钥PK与对称加密后的明文数据M, 最终计算生成密文CT, 并通过边缘节点上传云端存储。 (3)密钥生成算法 KeyGen(PP,MK,C,UID)→(SK,TKi,UID), 其中i表示用户属性。AA通过DU申请中的用户属性集合C与用户唯一标识符UID作为输入,同时将全局参数PP与主密钥MK加入运算,生成转换密钥TKi,UID, 绑定相应用户与属性。当用户所需属性分散在不同属性授权机构时,则需要向所有包含属性集合的AA提出密钥生成申请。DU生成私钥SK。最终获得完整用户私钥SK与完整转换密钥TK, 并将转换密钥TK交由域内边缘节点用于外包解密运算。 (4)数据解密算法包含2个子算法,分别为边缘节点预解密EN.Decrypt与用户终解密DU.Decrypt。 EN.Decrypt(PP,PK,TK,CT)→(CT′)。 边缘节点收到来自用户的数据申请请求与转换密钥后,向云端请求密文并运用转换密钥TK预解密得出转换密文CT′, 将其发送给申请用户。 DU.Decrypt(PP,PK,SK,CT′)→(M)。 DU在预解密的基础上只需要通过私钥SK进行少量运算开销解密即获得明文数据。 本节将对边缘环境下的多授权属性加密方案步骤进行详细描述。图2为系统方案数据流。该方案由4个算法构成:系统初始化算法、数据加密算法、密钥生成算法与数据解密算法。其中系统初始化算法分为全局初始化算法与属性机构初始化算法两个子算法,数据解密算法分为边缘节点预解密算法与用户终解密算法。 图2 系统方案数据流 阶段1:全局初始化算法 CA.Setup(k)→(PP) 阶段2:属性机构初始化算法 AA.Setup(PP)→(MK,PK) 输入全局参数PP, 由多个属性授权机构同时运行该算法。一个系统中往往存在多个属性授权机构,每个属性授权机构之间分别维护互不相交的自身属性列表,其属性列表的并集为全局属性集A。 针对每个被管理的属性i, AA选择随机值yi,ki∈p, 则输出属性主密钥MK={yi,ki|i∈A} 与公钥PK={yiG,kiG|i∈A}。 同时公开公钥PK, 保留主密钥MK。 阶段3:数据加密算法 Encrypt(PP,PK,(A,ρ),M)→(CT) 由DO运行该算法。首先数据拥有者根据自身访问策略构造LSSS访问结构 (A,ρ),A为m×n访问矩阵,ρ(x) 则表示矩阵A第x行所代表的属性。整个加密过程包括对明文数据对称加密和对对称密钥进行属性加密两者的混合加密方式。具体加密过程如下: (1)随机选取对称密钥ck,对明文数据M进行初步对称加密,从而获得第一密文Eck(M)=Enc(M,ck), 其中Enc() 表示对称加密算法。并计算数据Cn=H(Eck(M))G,这能够使DU在解密时验证明文数据的完整性。 (2)椭圆曲线上一点与密钥ck相映射,并选取随机秘密值s∈p, 计算获得C0=ck+sG。 (3)选取随机向量v,u∈Znp且v其第一位元素为随机值s∈Zp,u第一位元素为0。计算λx=Ax·v与ωx=Ax·u。 其中x∈[0,m-1],Ax则表示访问矩阵A的第x行。 (4)对于x∈[0,m-1], 选取随机数rx∈p, 计算得出C1,x=λxG+rxyρ(x)G,C2,x=rxG,C3,x=rxkρ(x)G+wxG。 由此,最终生成密文CT={(A,ρ),C0,E,Eck(M),{C1,x,C2,x,C3,x}x∈[0,m-1]}。 DO将密文CT通过边缘节点上传至云端存储。 阶段4:密钥生成算法 KeyGen(PP,MK,C,UID)→(SK,TKi,UID) 该算法由AA与DU运行。将全局参数PP、 主密钥MK、 用户属性集C与用户唯一标识UID作为输入,每个AA为用户属性集与自身属性列表的相交属性生成相应密钥。 设为用户UID的属性i生成密钥,为用户UID构建相关属性列表,并且对列表内所有属性i计算TK′={yi+H(UID)ki}i∈C。 将TK′发送至用户UID, 用户UID选取随机数z生成用户私钥SK={z}, 且变换转换密钥将其重新设计定义为TK-z, 即TK={yi+H(UID)ki-z}i∈C。 最终将转换密钥TK交由域内边缘节点用于外包解密运算,用户私钥SK由用户自身保留。 阶段5:边缘节点预解密算法 EN.Decrypt(PP,PK,TK,CT)→(CT′) 该算法由边缘节点EN运行。设由用户属性集C生成的集合X={x|ρ(x)∈C}, 若用户满足访问结构,即在多项式时间内能够通过常数集 {cx∈Zp}x∈X, 得到∑x∈XcxAx={1,0,…,0}, 由此可推∑x∈Xcxλx=s且∑x∈Xcxωx=0。 其中 Ax=C1,x-TK·C2,x+H(UID)C3,x= λxG+2rxG+H(UID)ωxG (3) D=∑x∈XcxAx=∑x∈Xcx(λxG+zrxG+H(UID)ωxG)= sG+z∑x∈XcxrxG (4) D′=∑x∈XcxC2,x=∑x∈XcxrxG (5) 则边缘节点将生成的转换密文CT′={C0,E,Eck(M),D,D′} 发送给数据使用者DU用于下一步解密。 阶段6:用户终解密算法DU.Decrypt(PP,PK,SK,CT′)→(M) 该算法由DU运行。用户得到转换密文CT′后通过C0-D+zD′=ck获得对称密钥ck。 通过对称密钥ck对数据进行最终解密,若能解密成功则说明数据未被篡改,反之则说明数据完整性被破坏。这是由于数据在加密过程中加入了Cn=H(Eck(M))G用以验证数据完整性且哈希[18]具有随机性与抗碰撞性[19]。 4.1.1 安全模型 本节主要通过将方案规约到DBDH假设[20]中,设计攻击游戏来建立安全模型,进一步证明本章方案具有选择明文攻击下的不可区分性(IND-CPA)。以下A为攻击者,B为挑战者。 证明:构建G为椭圆曲线E上大素数p阶、P为生成元的循环子群。挑战者B需选取随机数a,b,c∈p,β∈{0,1} 与R∈P。 Init:攻击者A首先定义访问结构 (A,ρ) 并将其发送给挑战者B。 Phase1:攻击者A将自身标识符UID对应属性 (i,UID) 提交给挑战者B,以求用户属性集所对应属性私钥。挑战者B选取随机值t,l∈p, 并用其计算转换密钥提交给攻击者A。攻击者A计算整合转换密钥集合TK′={yi+H(UID)ki}i∈C, 接着攻击者A选取随机数z生成自身私钥SK={z}, 设置转换密钥为TK-z, 即TK={yi+H(UID)ki-z}i∈C。 事实上攻击者A由于自身属性集合不符合访问结构因此所求密钥组并不能成功解密数据。 Challenge:攻击者A向挑战者B发送等长的两组数据信息m0与m1, 挑战者B选择随机参数β∈{0,1}, 执行上节阶段3数据加密算法对明文数据mβ进行运算。最终将密文CT={(A,ρ),C0,{C1,x,C2,x,C3,x}x∈[0,m-1]} 发送给攻击者A。 Phase2:攻击者A能够提交同Phase1相同限制的 (i,UID) 密钥查询申请。 Guess:攻击者提出对β的猜测β′。 若相等,则挑战者B输出1;反之B输出0。当输出为1时,攻击者A能够获得有效密文。由此可知概率优势为式(6) AdvIND-CPA=|Pr[β′=β]-1/2| (6) 若攻击者A赢得游戏的优势不可忽略,则挑战者B攻破DBDH假设的优势则同样不可忽略。但DBDH假设是公认的数学困难问题假设,因此挑战者B的优势则不存在不可忽略的情况,反推攻击者A赢得游戏的优势也不成立,从而得证方案在选择明文攻击下的安全性。 4.1.2 安全性分析 本节将分别从防篡改攻击、数据安全性和抗合谋攻击3个角度分析了本方案的安全性。 (1)防篡改攻击。随机选取对称密钥ck, 对明文数据M进行初步对称加密,从而获得第一密文Eck(M), 并计算数据Cn=H(Eck(M))G。 由于哈希函数具有唯一性与不可逆性且ck为系统随机数,用户不可复制,因此用户若无法解密则说明密钥出现问题,则数据存在被篡改的可能。通过该方式本文方案能够保证系统在主动篡改攻击下的安全性。 (2)数据安全性。由于只有满足属性集合且满足属性阈值的用户属性授权机构才会授予其相应属性主密钥 {yi,ki}, 又由于方案基于ECC算法,而椭圆曲线上的离散对数问题具有困难性,故无效用户无法通过系统公开密钥 {yiG,kiG} 倒推出主密钥信息。同时明文数据M被对称密钥ck加密后,对称密钥ck通过DO自主选择的随机数s, 被映射至椭圆曲线E上的随机点。由于ECDLP的困难性,攻击者无法获得关于明文数据M的任何信息。而LSSS中随机秘密值s也表明了当用户不满足访问策略结构时无法获得私钥,即不存在属性ρ(i), 无法推得随机向量v中秘密值s。 因此本文方案具有数据安全性。 (3)抗合谋攻击[21]。主要从两方面考虑。首先是不同数据用户之间的合谋,即要防止多个无法独立解密的用户相互勾结,互相之间集合属性来达到获得完整所需属性集并解密的目的。本文方案中密钥生成阶段的用户私钥与转换密钥均与具体用户属性ρ(i) 与用户唯一标识符UID绑定。也就是说,系统能够通过密钥中的标识符信息识别属性密钥集中的每个密钥是否来自同一个用户,若出现多个不同UID, 则无法使∑x∈Xcxλx=s, 继而无法计算恢复sG, 说明该属性集具有合谋嫌疑,则不予以解密。其次是边缘节点与数据用户之间的合谋攻击。当边缘节点将预解密后的转换密文CT′发送给不具备访问权限的用户UID′, 用户UID′进行终解密时需要用户私钥SK, 而私钥是由随机生成的随机数z构成,不同用户所生成的随机数z不同,私钥也不同,不正确的随机数z无法对转换密文CT′进行终解密,从而用户无法获得真正的明文信息M。 从以上两方面的合谋攻击分析可知,本章提出的EMO-ABE方案具有抗合谋性。 4.2.1 理论分析 本节将Odelu方案、Zhang方案、Liu方案与本文方案就系统功能与计算开销进行比较分析。表1为3种方案的系统功能对比。 表1 方案系统功能对比 通过上表我们可以发现Odelu方案使用与门作为访问结构,缺点是结构过于单一,不能够灵活处理访问结构的变化。并且其使用单一授权机构,可能出现的单点失效情况和密钥托管问题。同时该方案与Zhang方案中解密操作都在用户端处理,将会给用户端带来较大计算负担。此外,Zhang方案与Liu方案使用双线性配对会给系统带来多余的指数运算与双线性运算,从而增加额外的运算开销。而本文方案中用LSSS来构造访问结构,使系统更加方便灵活,同时将属性分散至多个属性授权机构,有效避免了上述问题,并将传统属性加密算法中的双线性配对替换为椭圆曲线加密中的简单标量乘法,以此减少计算开销提升加密效率,最后将解密操作外包至边缘节点,使得用户只需要进行简单计算操作即可获得明文数据。 为从计算开销方面分析上述3种方案与本文方案的对比,通过表2说明本节用到的符号及对应说明。 表2 符号及对应含义说明 表3为上述3个方案之间的计算开销对比。从表中可以看出Odelu方案与Zhang方案未实现外包实现功能,故其用户解密开销将随访问策略的复杂度升高而升高,而Liu方案与本方案由于引入了外包所以用户解密成本非常稳定且低。同时Liu方案由于其需要通过多次双线性与指数操作给加解密带来了巨大的开销。 表3 方案计算开销对比 4.2.2 实验仿真 为了证明和体现方案达到的可行性与有效性,将本文方案与Odelu方案、Zhang方案、Liu方案从不同属性数目时DO加密时间、用户解密时间与外包运算时间进行性能观察并比较。具体环境参数见表4。 表4 实验环境参数 图3为数据拥有者数据加密时属性数量与运算时间关系图。从图中可以看出,4种方案总体运行时间都随着属用性数量的增加而增长,其中Zhang方案由于引入了可追溯性导致其运算时间要更大。而Odelu方案与本文方案由于用椭圆曲线中的简单标量乘法代替了双线性配对,减少了双线性计算带来的巨大开销,使得计算量与运行时间上明显少于另两种方案。本方案运用秘密共享矩阵构造访问策略使得属性更灵活因此运行时间要更优。 图3 数据拥有者加密阶段运行时间 用户DU在解密阶段的运行时间与属性数量之间的关系如图4所示。从图中可以看出,Zhang方案由于具备了可追溯性功能,虽然在安全性上得到部分提升但不可避免的付出了计算开销上的代价,其与Odelu方案的用户解密阶段上属性数量依旧是影响运行时间的最大因素。而Liu方案与本文方案由于引入了外包预解密使得用户在解密阶段只需要进行简单操作即可获得符合自身属性集的数据信息。 图4 用户解密阶段运行时间 图5为边缘节点上外包解密的运行时间与属性数量关系图。由于只有Liu方案引入了外包功能,因此该实验只将Liu方案与本文方案进行对比。从图中可以看出,解密阶段的大部分开销均发生在边缘节点处,用户端不需要进行复杂操作,同时由于本文方案在边缘层解密阶段时用椭圆曲线中的简单乘法标量代替双线性映射计算,减少了双线性配对计算与指数计算的次数,因此降低了运算时间。 图5 边缘节点外包解密运行时间 本文提出一种应用在边缘环境下的多授权属性加密方案。摒弃传统属性加密的双线性映射,用椭圆曲线上的简单标量乘法替代,并且引入边缘节点,将由用户承担的解密计算外包至边缘节点,以此减少计算开销提升加密效率。最后通过多授权中心分摊属性管理机制,避免了单一授权机构可能出现的单点失效情况和密钥托管问题。同时未来也需要进一步研究如何在边缘计算场景中,进一步提高系统的稳定性,以及如何降低网络交互带来的传输时延。在边缘计算未来发展的趋势下,边缘环境能够运用到更多领域,拉进云平台与用户之间的通信距离,提供更细粒度的访问控制服务,并发展至更广泛的应用。2 系统模型
2.1 整体框架
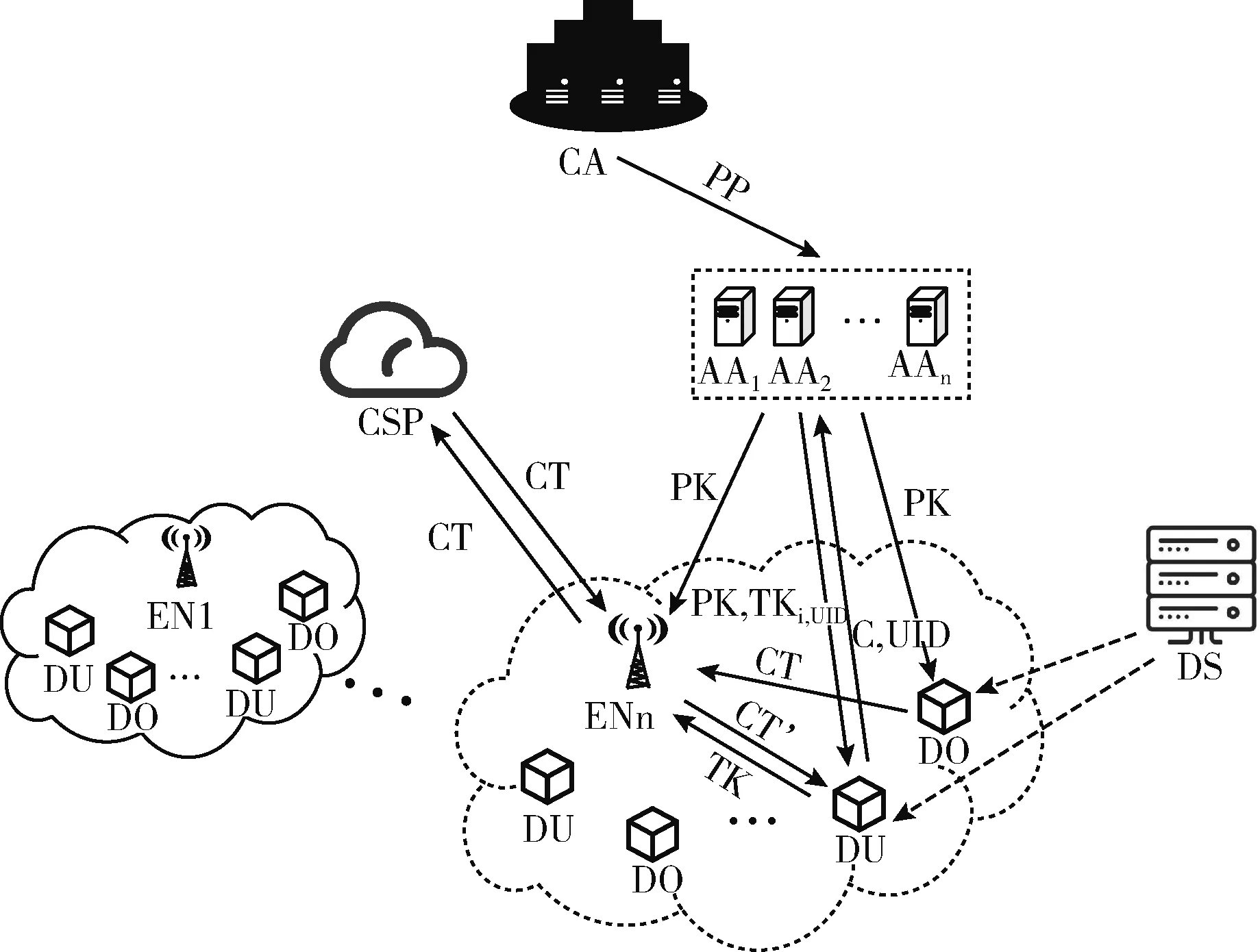
2.2 算法概述
3 具体方案构造


4 安全分析与性能分析
4.1 安全分析

4.2 性能分析


5 结束语
