基于标定冲击系数的锤击过载计算方法

柳海斌,李 冰,高 阁

(1.西安机电信息技术研究所,陕西 西安 710065;2.机电动态控制重点实验室,陕西 西安 710065;3.中国兵器工业试验测试研究院,陕西 华阴 714200)

0 引言

锤击试验是引信、火工品常用的过载试验方法,用于评价引信零部件强度和火工品安定性,具有操作简单、经济实用的特点。锤击机利用了碰撞冲击原理,冲击过载和撞击面形状、材料特性、齿数、工装及配重等有关,WJ 233—1977规定了锤击机技术参数、验收规则和使用要求,WJ 2257—1994规定了锤击机23齿、专用击锤条件下的加速度检定值。锤击机过载持续时间短,一般只有数十微秒,通常只能用来模拟过载峰值。

文献[1]介绍了3类等效模拟循环锤击试验方法,提出了“等效损伤或破坏程度,不等效实际激励”的概念,用于激发强度薄弱部位,评估引信对火炮高过载发射环境的适应性,在中大口径榴弹类引信研制、生产、试验中经常使用。文献[2]给出了不同配重、不同齿数下的锤击加速度测试值。文献[3]给出了锤击峰值加速度计算公式,由于缺乏验证,仅在分析加速度影响因素时参考使用。文献[4]介绍了冲击试验台半正弦波脉冲峰值加速度公式:

(1)

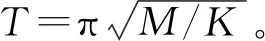
文献[5]给出了一端固定、长度为L的杆在自由端受到运动物体撞击后的接触时间:

(2)

式(2)中,C为应力波在杆中的传播速度,μ为运动物体与杆的质量之比。

对于WJ 233—1977锤击机不同配重不同齿数的锤击过载计算、已知过载要求和受试品配重如何确定试验齿数问题,未见相关文献报道。本文针对锤击机缺少齿数、配重、过载对应关系,造成使用不便的问题,提出标定冲击系数计算锤击过载的方法。

1 锤击过载的产生

1.1 锤击机原理

试验件通过辅助工装安装在锤击机击锤上[6],击锤通过锤柄安装到半圆轮上,半圆轮通过机轴与机架连接。重锤悬挂在半圆轮上,用于提供半圆轮旋转的动力。机轴上安装有棘爪控制的棘轮,棘轮共有30个齿,每个齿对应12°转角。试验时将击锤升高一定齿数,通过棘轮、棘爪将半圆轮固定。释放棘爪后,半圆轮在重锤重力作用下旋转,锤柄旋转至水平位置时,击锤以一定的速度击打铁砧,产生惯性冲击力。击锤升高的齿数越高,产生的惯性冲击力越大。允许使用的最高齿数为23齿。

锤击机主要特征参数[7]:

1) 击锤质量640 g±10 g;

2) 锤柄质量2 kg±0.5 kg;

3) 重锤质量36.5 kg±0.1 kg;

4) 吊环和螺母总质量(连接重锤和半圆轮)500 g±10 g;

5) 击锤、铁砧中心线到机轴的距离为800～810 mm;

6) 击锤落到铁砧上时(0齿)半圆轮斜边与垂直线的夹角为12°±1°;

7) 23齿冲击加速度为28 400～31 400g。

1.2 碰撞冲击过程

碰撞冲击过程中运动体在短时间Δt内发生速度变化Δv,从而产生冲击加速度,根据加速度定义:

a=Δv/Δt。

(3)

根据应力波理论,两弹性体接触碰撞过程中产生压缩应力波,弹性碰撞通过应力波传播[8],应力波速度为

(4)

式(4)中,E为材料杨氏模量,ρ为材料密度。应力波在弹性体自由端反射形成卸载波,当接触面处应力卸载到σ=0时,碰撞结束,对应的碰撞接触时间为

t=2L/C,

(5)

式(5)中,L为长度较短的弹性体长度。

2 冲击系数法计算锤击过载

2.1 齿数与击锤撞击速度的关系

将半圆轮、锤柄、击锤及受试品视为绕机轴O运动的刚体,忽略其绕机轴转动的能量损失,同时忽略连接重锤和半圆轮的吊带在绕半圆轮释放过程中质心的变化,锤击机运动模型见图1。

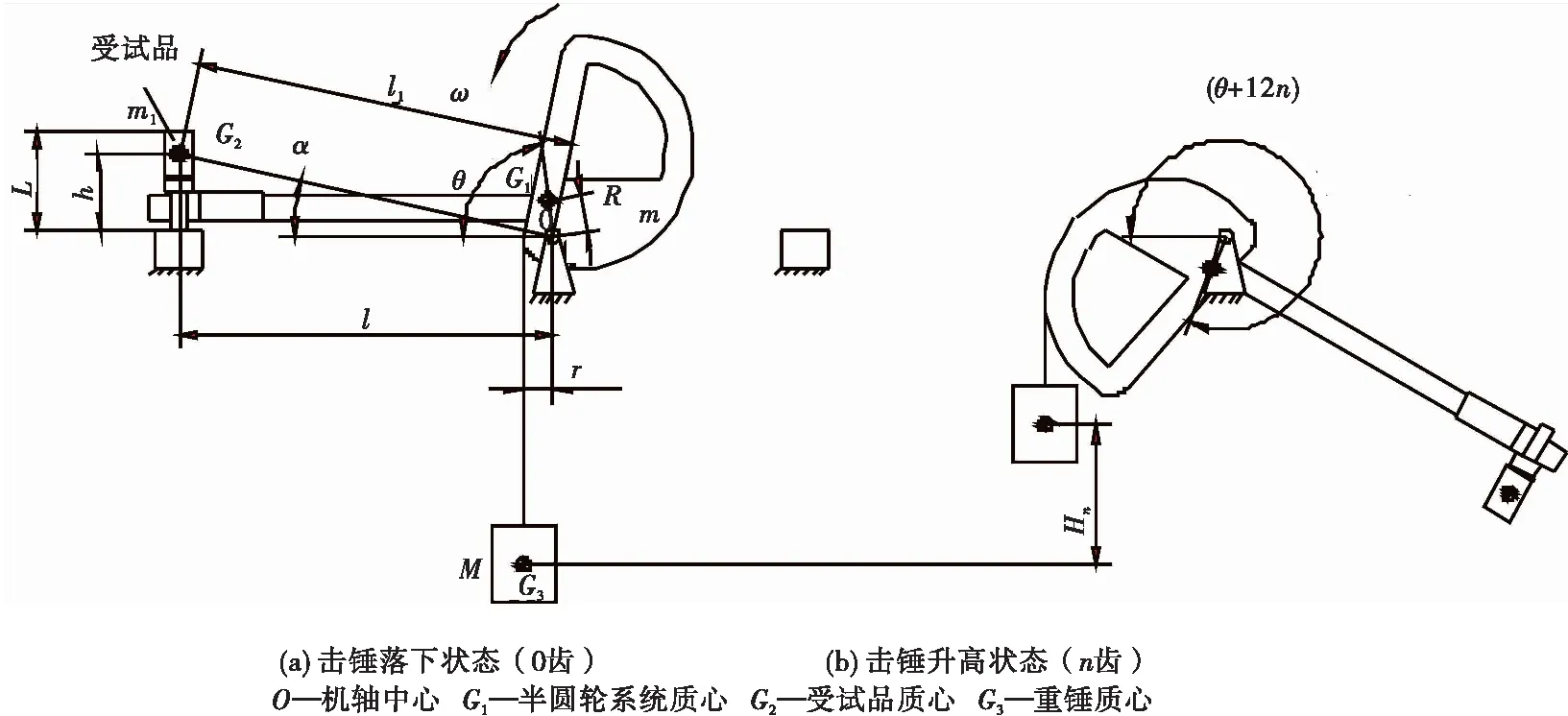
图1 锤击机运动模型

根据能量守恒原理,建立锤击机运动方程:

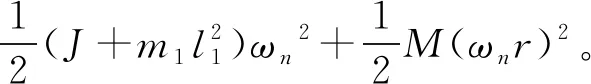
(6)

击锤升高n齿,对应击锤与铁砧接触瞬间的碰撞速度:

Vn=ωn·l,

(7)

式(6)、式(7)中,M为重锤、吊环、螺母总质量,m为半圆轮系统质量(含机轴、锤柄、击锤、棘轮),m1为受试品质量,n为升高齿数,R为半圆轮系统质心距机轴的距离,r为击锤与铁砧接触瞬间重锤速度方向距机轴的距离,L为击锤和受试品总高,l为击锤中心距机轴的距离,l1为受试品质心距机轴的距离,Hn为n齿对应的重锤升高量,h为受试品质心高度,θ为0齿时半圆轮系统质心水平夹角,α为0齿时受试品质心与机轴连线的水平夹角,J为半圆轮系统相对机轴的转动惯量,ωn为n齿对应的击锤与铁砧接触瞬间半圆轮系统角速度。

2.2 测定所用锤击机在典型齿数下的冲击参数

对于试验所用锤击机,在工装、配重相同条件下,采用加速度计选取典型齿数测试冲击过载值an。确定所用测试工装和加速度计总质量m1、安装在击锤上之后的质心位置h,利用式(6)、式(7),计算典型齿数对应的击锤速度Vn。

2.3 冲击系数计算锤击过载原理

假设条件:

1) 铁砧与击锤碰撞为正碰撞;

2) 碰撞恢复系数(反跳系数)β与击锤及铁砧材料、击锤碰撞面形状、碰撞速度有关;

3) 击锤与铁砧接触瞬间碰撞开始,此时击锤速度为Vn。击锤与铁砧首次碰撞分离时刻碰撞结束,对应击锤速度为βn·Vn,碰撞接触时间为应力波在击锤中的往返传播时间。

则根据式(3)—式(5),得到n齿下的锤击冲击加速度:

(8)

定义冲击系数Kn=(1+βn)C/2L,则

an=KnVn。

(9)

可以看出,对于同一台锤击机,在同一工装或受试品测试条件下,齿数n与齿数m冲击系数比为

Kn/Km=(1+βn)/(1+βm)。

(10)

对典型齿数冲击过载测试值an和击锤速度Vn,利用式(9)可以计算出典型齿数对应的冲击系数Kn。

根据假设条件2),由于击锤及铁砧材料、击锤碰撞面形状相同,碰撞恢复系数仅与碰撞速度有关。因为碰撞速度变化不大时,碰撞恢复系数变化亦不大,所以对某一配重下n齿和m齿的冲击系数比,可以从典型齿数击锤速度、冲击系数中,选择与其速度最接近的两个齿数的冲击系数比近似代替。

当已知某一配重下齿数n的过载值时,即可计算出另一齿数m对应的过载值:

(11)

2.4 锤击过载计算

锤击过载计算步骤:

1) 确定所用锤击机模型参数,试验配重质量、质心参数,利用式(6)、式(7),计算试验配重对应的23齿及其他所需齿数的击锤速度Vn;

2) 用与试验配重材料相同,结构、质量等效的工装标定试验配重23齿所对应的冲击过载值a23;

3) 选取典型齿数,如5齿、10齿、15齿、18齿、23齿,用加速度计测试典型齿数对应的冲击过载值an,计算典型齿数对应的击锤速度Vn和冲击系数Kn,从而确定锤击机典型齿数下的击锤速度-冲击系数特征值;

4) 根据步骤1)计算得出的试验配重在23齿和所需试验齿数下的击锤速度,对照步骤3)击锤速度-冲击系数特征值参数,依据“速度最接近”原则,选取对应击锤速度下的冲击系数;

5) 利用式(11),计算试验配重在所需试验齿数下的冲击过载值。

3 验证与结果分析

3.1 锤击过载计算

根据WJ 2257—1994锤击机特征参数,结合实物测绘数据,复核锤击机结构尺寸、质量、质心参数,采用INVENTOR三维机械设计软件建立半圆轮系统(含机轴、锤柄、击锤、棘轮)三维实体模型见图2,得到锤击机模型参数见表1。

表1 所用锤击机模型参数

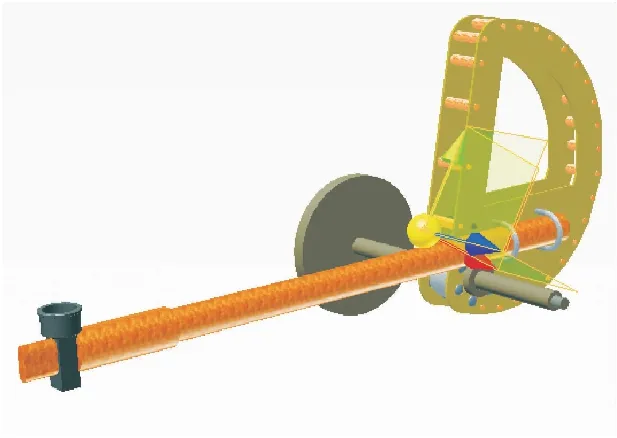
图2 半圆轮系统三维实体模型

采用同一击锤,选取5齿、10齿、15齿、18齿、23齿进行锤击过载测试。加速度计及测试工装如图3所示。锤击机冲击系数测试用工装质量(含加速度计)1 050 g,选取配重为1 810、1 190、810 g的工装分别进行测试。工装配重参数及击锤速度见表2。锤击机冲击系数Kn测定结果见表3。

表2 工装配重参数及击锤速度

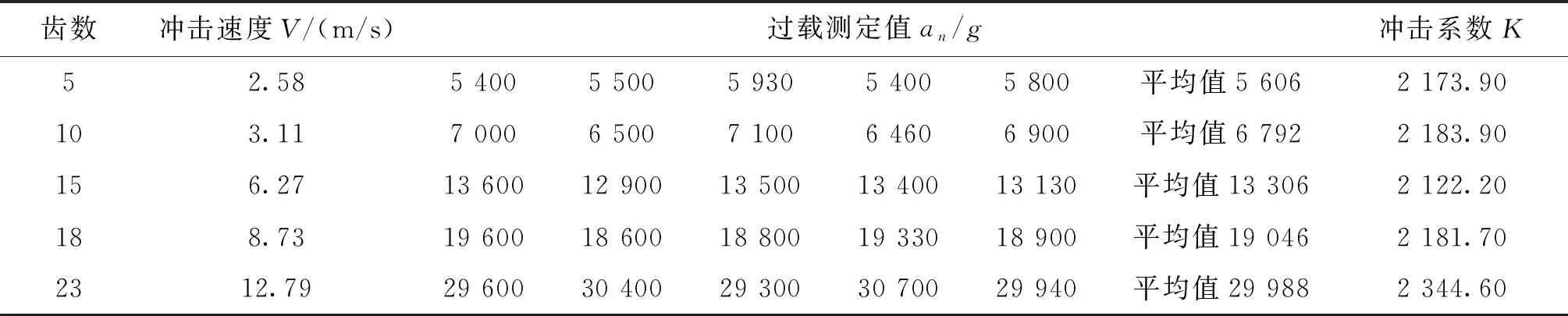
表3 锤击机冲击系数测定

图3 锤击机23齿标定

利用加速度计标定工装A的23齿冲击过载值a23,代入式(9)计算工装A在23齿下的冲击系数K23。根据表2计算结果,工装A 23齿、18齿冲击速度与冲击系数测试工装23齿、18齿冲击速度接近,根据2.4节锤击过载计算方法和2.4节4)“速度最接近”原则,工装A 23齿、18齿冲击系数比可以用冲击系数测试工装K23/K18近似代替,利用式(11)计算得到工装A对应的18齿冲击过载计算值。同理可得到15齿、10齿、5齿冲击过载值。工装A、工装B、工装C冲击过载计算及测试结果见表4。

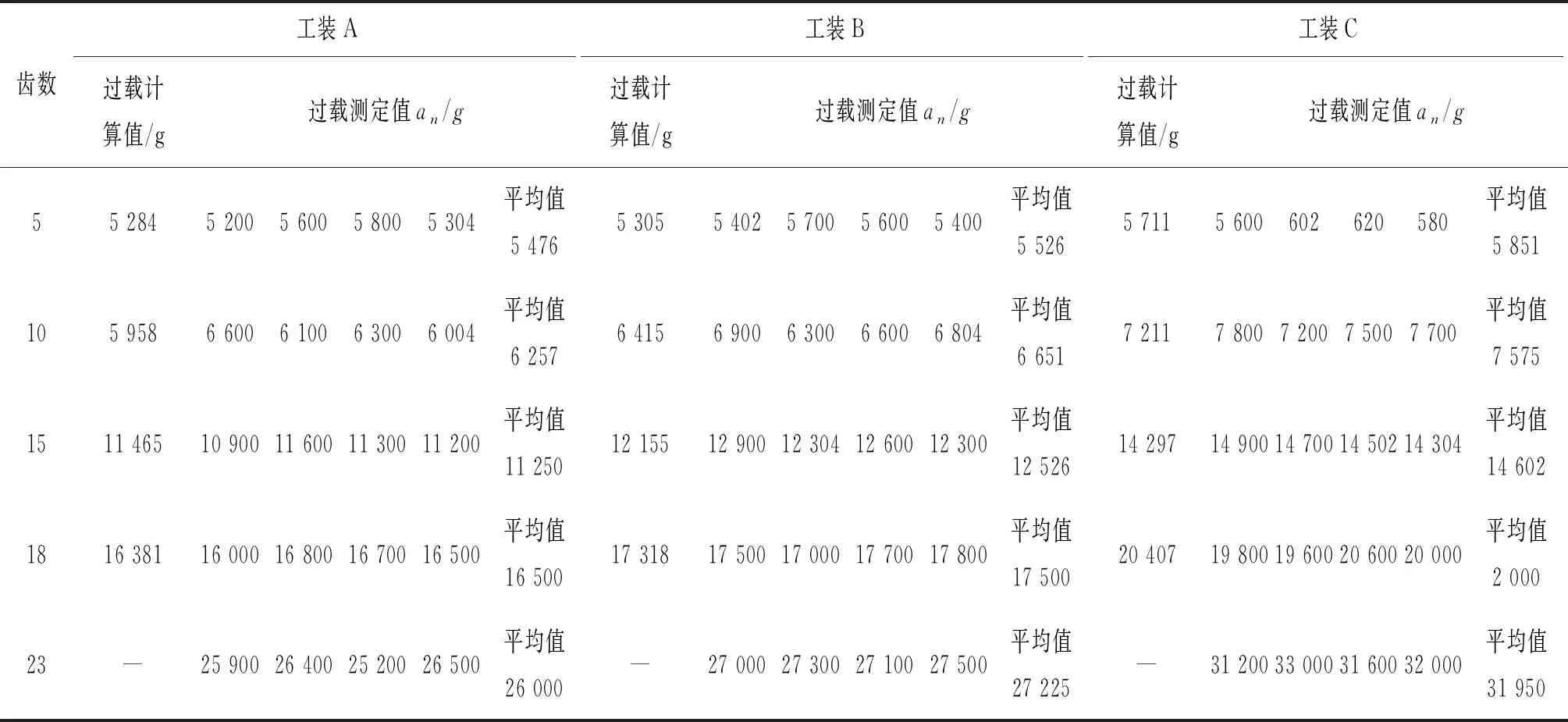
表4 不同配重锤击过载的计算值和测试值

3.2 结果分析

从表2不同工装配重下的击锤速度计算结果来看,15齿、18齿、23齿击锤速度随配重变化明显,符合同一配重齿数越高速度越大、同一齿数配重质量越轻速度越大的规律。5齿、10齿击锤速度随配重变化不明显,5齿时工装A配重最重,速度却略高于其他工装,主要原因是锤击机模型参数的影响,根据1.1节特征参数散布范围,偏差分别取上下限时,15齿、18齿、23齿击锤速度计算偏差约为5%,5齿、10齿速度偏差接近10%,说明速度计算公式及模型参数对高齿数适应性较好,低齿数时计算误差变大。

从表4不同配重锤击过载的计算值和测试结果对比来看,冲击过载计算值与测试结果基本符合。15齿、18齿、23齿过载测试结果与计算值符合较好,同一配重齿数越高冲击过载值越大,同一齿数配重质量越轻冲击过载值越大。5齿、10齿也符合同一配重齿数越高过载越大、同一齿数配重质量越轻过载越大的规律,但冲击过载值随配重质量变化不明显,尤其5齿时,工装A、工装B过载十分接近,说明低齿数使用时试验配重对过载值影响相比高齿数要小。

试验所用锤击机23齿冲击加速度检定值为29 988g,符合WJ 2257—1994 23齿冲击加速度检定要求。表3锤击机冲击系数测定配重1 050 g,与文献[2]1 045 g测试配重接近,过载测试值数值接近略有不同,考虑到引信、火工品行业使用的锤击机制造年代、厂家不同,并且击锤形状也有所不同 ,因此使用本文方法计算锤击过载前首先需要确定锤击机模型参数,测定不同齿数的冲击参数以确定冲击系数非常必要。锤击机参数散布引起的击锤速度散布是影响冲击过载计算结果的主要因素,研究适用于击锤速度测试的方法和装置,准确测试击锤速度,可以解决锤击机模型参数不易准确掌握、速度计算误差较大的问题,能够进一步提高本方法的工程适应性。

综上分析,采用标定冲击系数计算锤击过载的方法反映了锤击过载和配重、齿数的关系,对15齿、18齿、23齿高齿数的计算偏差小于4%,对5齿、10齿低齿数的计算偏差小于7%,能够用于锤击机过载值的工程计算。

4 结论

本文提出了标定冲击系数计算锤击过载的方法,该方法利用能量法建立锤击机运动模型并计算击锤速度,基于加速度定义和应力传播的弹性碰撞接触时间推导出锤击加速度大小等于冲击系数和击锤撞击速度的乘积,通过标定获取锤击机典型齿数的冲击系数,利用试验配重在某一齿数下的过载测试值计算其他齿数的过载值。验证和分析结果表明,标定冲击系数计算锤击过载方法反映了锤击机冲击过载和配重、齿数的关系,对15齿、18齿、23齿高齿数的计算偏差小于4%,对5齿、10齿低齿数的计算偏差小于7%,能够用于锤击机过载值的工程计算。本文方法不足之处在于采用锤击机运动模型计算击锤速度,由于锤击机准确模型参数不易获取,不同齿数的击锤速度对锤击过载值计算影响较大,需要继续研究击锤速度测试方法和装置,以减少模型速度误差的影响,进一步提高计算精度。