学习进阶视域下除数是整数的小数除法教学探析
2023-09-12方苏云赵易莛
方苏云 赵易莛


【摘 要】学习进阶视域下的小学数学课堂教学,是指学生在学习和探究某一知识时,对该知识的认识和思考不断深入、精致和完善,逐步实现知识层级的跨越,最终获得思维与素养的进阶发展。本文依托“学习进阶”理论,精心设计除数是整数的小数除法的学习进阶层级建构策略:把准“低起点”,调用已有经验初步感悟算理;激活“中间水平”,连续深入理解算理与算法;实现“高落点”,综合运用内化算法。
【关键词】小学数学 学习进阶 小数除法
“除数是整数的小数除法”是人教版五上小数除法单元的关键起始课例,教材编排三个例题分两课时完成,知识点逐步递进如图1所示。
从教材编排来看,编者主要创设跑步情境利用千米和米的关系,同时结合小数的意义帮助学生理解除数是整数的小数除法算理,探索商的小数点的定位方法。与整数除法相比,小数除法的计算过程步骤更为繁琐,这主要是学生对小数由计数单位逐步均等细分产生的过程较难建立具体的表象,进而直接影响其对小数除法算理的理解。
学习是一个进阶的过程,学习进阶视域下的课堂教学,就是指学生在学习和探究某一知识时,对该知识的认识和思考不断深入、精致和完善,注重对新知识的“整体”与“深层”建构,逐步实现知识层级的跨越,最终获得思维与素养的进阶发展。本文依托“学习进阶”理论,精心构建符合除数是整数的小数除法运算发展序列和学生认知规律的层级,引领学生展开进阶学习,深度理解小数除法算理,掌握运用算理的方法。
一、建立:除数是整数的小数除法学习進阶
《义务教育数学课程标准(2022年版)》提出“数与运算”主题,体现数概念与运算的密切关联。整数的运算基于学生对整数意义的理解,那么小数的运算也基于对小数意义的理解。依托小数十进制的特征,着眼计数单位展开除数是整数的小数除法的学习,将教材编排的两课时内容整合为一课时,实现学习内容的整体设计——将被除数计数单位变小,其数变大,成为整数,再融合小数意义图像理解小数除法计数单位均等细分的算理图式,进而深刻理解其本质内涵。
基于上述思考,为更精准地建立学习进阶层级,笔者对处于城郊结合部的某所学校五年级的两个班共84个学生进行前测,前测题如下:①王鹏坚持晨练,计划4周跑步22.4千米,他平均每周跑步多少千米?②妈妈去超市买了5袋牛奶,共花了11.5元,每袋牛奶多少元?前测结果显示,题①正确率为66.7%,题②正确率为83.3%。
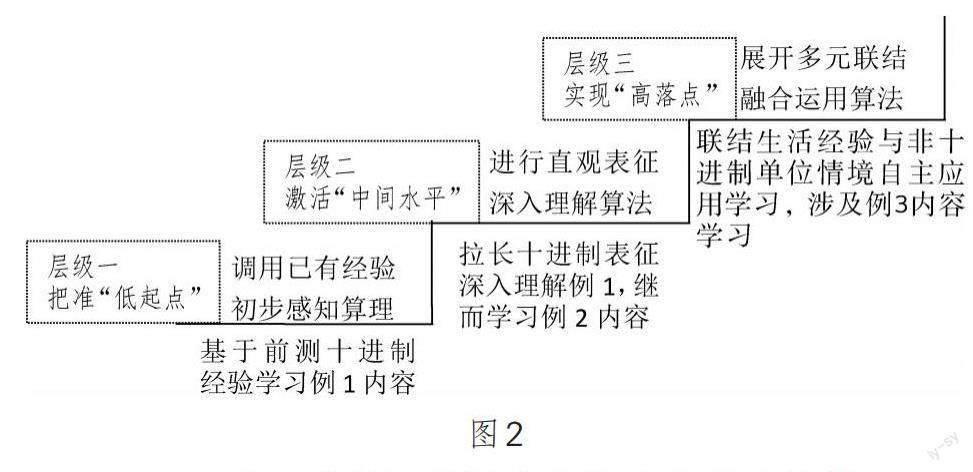
从前测结果看,学生对十进制单位情境下的除数是整数的小数除法前认知比非十进制单位情境下的更厚实,这与具有十进制特征的小数意义紧密关联。小数除法的基石是由计数单位的均等细分构建的,因此从学生已有丰厚的十进制经验出发建构学习层级,更易于激发学生对知识的自主建构与理解小数除法算理。据此,笔者建立了除数是整数的小数除法学习进阶层级(如图2所示)。用三个层级统整原教材中两个课时的三个例题,在实现内容结构化的同时,发展学生的运算能力、几何直观和推理意识等核心素养。
二、实践:除数是整数的小数除法进阶教学
(一)把准“低起点”:切入十进制单位情境,调用已有经验初步感悟算理
依据前测可知,学生在学习除数是整数的小数除法之前,已经初步具备了学习小数概念及进行十进制单位换算的经验,因此,学生在学习本节课内容时,完全可以对接自身已有的经验,初步感知除数是整数的小数除法算理。
1.对接已有经验,引发认知冲突。
【教学片段1】大屏幕呈现图3。教师先提问:“同学们课前做的这道题,有这么多种方法,你们都能看懂吗?你们认为哪些是正确的,哪些是不正确的?”引导学生观察、对比、分析,进而产生学习需求——余数是小数时怎么继续除。
此环节基于80%以上的学生会正确计算的情况下展开观察讨论,引导学生在对比中自然对接已有的经验来辨析对错,比如:①号运用十进制单位换算,②号利用商的变化规律,④号将“1.5元”也运用十进制单位换算并画图形象表示,以此得到正确结果。从中,学生产生了学习需求。在这个过程中,学生的已有经验被唤醒,激起了思考的欲望,切准学习进阶的支点。
2.修正偏差经验,初步感知算理。
学生在整数除法中已积累有余数除法的经验,如何修正这种对小数除法来说有所偏差的经验呢?笔者利用学生积累的十进制单位换算的经验,巧妙连接学生前测⑤号的正确竖式、③号的偏差竖式及④号的直观图进行修正。
【教学片段2】教师提问:“仔细观察④号的图,你能说说余数是小数时怎么继续除吗?为什么⑤号这样写就对了呢?”引导学生上台指着④号的图说1.5元等于15角,就可以写成⑤号竖式中的“15”,15角平均分成5份,每份是3角,就是0.3元。
在上述过程中,笔者直接利用④号的直观图联系⑤号竖式,来修正学生认知中的偏差(③号竖式),初步感知余数是小数能继续除的道理——把单位“元”变成“角”,数大了就可以继续除。将原教材中的跑步情境换成购物的情境,在十进制单位情境中纠偏能更容易沟通整数除法和小数除法的意义,实现了意义层面的整体关联,学习推进可谓是拾级而上。
(二)激活“中间水平”:拉长十进制表征,连续深入理解算理与算法
对除数是整数的小数除法算理的理解不是一蹴而就的,需要通过一个“中间水平”逐步过渡形成。十进制“元、角、分”的表征固然形象易于理解,但对算理的理解还需要形成一般表征的抽象过程,才能最终成为印在学生脑海中更抽象的算理与算法。
1.第一次表征,进一步理解“‘几个一均分继续除”。
【教学片段3】教师提问:“如果一个方形表示1元,这样的11个加半个就是11.5元,那11.5÷5的计算过程怎样表示呢?谁能来说一说?”教师边说边在屏幕上呈现图4中的方形,指名学生上台说,并在屏幕上表示出圈画的过程。11.5平均分成5份,每份有这样的2个,还剩下1.5(如图4)。教师追问:“那1.5怎么继续往下分呢?”
为了便于学生表达,将图4中表示1.5个一的图形放大呈现,请学生说出继续把1.5平均分的思考过程。教师根据学生的回答适时点拨:1.5也就是1.5个一,像图5这样平均分后就转换成了15个十分之一,把它平均分成5份,每份就是3个十分之一,也就是0.3。自然在屏幕上形成图6,这样每一份就是2个一加3个十分之一。再呈现竖式(如图7),教师追问:“你能在图6中找到竖式中的每一个数吗?”引导学生进一步联系“式”与“图”,理解竖式每一步的意义。
此环节是本课的重点,笔者有意将学生思维从“元角分”十进制单位中脱离出来,借助面积模型表征对算理理解进行了适度的抽象,帮助学生理解。在师生、生生的互动对话中激活学生的思维,在具体“形”的均分过程中对接“竖式”中的每一个数,实现“余数是小数时可以继续除”的思维跨越,学生的思维水平得到晋级。
2.第二次表征,类推理解连续均分继续除。
在学生理解了“几个一”转化成“几个十分之一”再继续除后,可以趁热打铁,推进“几个十分之一”不够除时就转化成“几个百分之一”,“几个百分之一”也可转化成“几个千分之一”继续除,等等。激活学生类比迁移的隐性思维,提升学生的运算能力。
【教学片段4】继续沿用购物情境:超市促销活动,同样的20袋牛奶需要41.6元,那么现在每袋牛奶多少元?请你试着解决。引导学生独立完成,再与同桌交流方法。展示学生方法,主要集中在两种(如图8),先让学生说说自己的想法,再引导结合方形图来说一说。屏幕呈现图9,分完40时,对剩下的表示1.6的图形放大动态演示成为16个十分之一(如图10)。此时教师追问学生:“16个十分之一平均分成20份还是不够除,又该怎么办?”学生顿悟——继续平均分。
根据学生的回答再动态演示图11,教师追问:“现在变成多少了呢?”在追问中激活学生的学习经验,十分之一均分10份后就是百分之一。教师继续追问:“那160个百分之一平均分成20份,每份是多少呢?”在大屏幕上清晰表示出每一份是8个百分之一,那么现在每袋牛奶就是2.08元(呈现图12),最后与图13的竖式对接。
此环节不仅是学习内容的进阶,更是学生思维的进阶。学习内容在指向教材例2“除到被除数末尾有余数,须补0再除”的同时,还指向商中间有0的小数除法。考虑到“商中间有0”是整数除法中学生的易错点,笔者将这个易错点加以迁移、整合,在连续转化计数单位的过程中借助直观表征来有效突破这一难点的理与法。再次以购物情境对接“元角分”十进制经验,利用图形不断均分,实现学生思维的可视化。在实际教学推进过程中,笔者还增加了一个追问“如果除到160,还有余数怎么办呢?”通过这样的追问帮助学生建立起拓展式的思维图式和整体思考策略,促进学生推理意识的形成。
(三)实现“高落点”:联结非十进制单位情境,综合运用内化算法
学习进阶视域下的小学数学教学,既要重视学生整体知识的建构,又要在认知深度上做好推进。在本课的教学中,教师的视角不能仅限于“十进制”单位支撑下的理解,还可以联结“非十进制”单位等其他情境不断挖掘运算的宽度和广度,实现学生认知水平、思维发展和运用能力的三重提升。
1.联结生活实际,丰富解决问题策略。
【教学片段5】在学生理解了小数除法的算理与算法后,教师联结生活实际,再一次对比图8的两种方法并提问:“根据信息中的‘促销活动,你又想到了什么呢?”引发学生联系“商品促销”的现实意义,明白了图8中“2.8”比原价“2.3”贵了,可以肯定计算出了错误。
运算方法的形成和掌握,除了理解知识的本质内涵外,也离不开外延的丰富与扩展。运算与解决问题总是紧密相连的,在上述过程中,通过一个提问来激发学生思考,联结生活实际反思用数学解决实际问题,赋予抽象的数学知识以现实意义。在联结中反思,在反思中运用,丰富了学生解决问题的策略。
2.联结非十进制单位,提升综合应用能力。
【教学片段6】屏幕呈现:“超市营业员李阿姨要用一根长7.8米的彩带,包装37.8千克糖果,正好能包装12个礼盒。请你提出一个用小数除法解决的问题并解答。”让学生在计算“7.8÷12”中完善例3“被除数整数部分不够商1,0占位”的計算方法,在计算“37.8÷12”中巩固前面习得的计算方法。
为避免连续“十进制”单位情境带来的负迁移,笔者进阶设计了“非十进制”单位情境的解决问题环节。此环节让学生在“非十进制”单位情境中完善、巩固除数是整数的小数除法的方法,帮助打通思维阻碍,助力“四能”与核心素养的形成。
(作者单位:浙江省杭州市富阳区教育发展研究中心 浙江省杭州市富春大青小学)
