用于弱电网互联的柔性直流输电系统双端构网型控制

蔡海青，郭 琦，杨仁炘，黄立滨，施 刚，顾浩瀚，苏明章

（1.南方电网科学研究院有限责任公司 直流输电技术全国重点实验室，广东 广州 510663；2.国家能源大电网技术研发（实验）中心，广东 广州 510663；3.上海交通大学 电子信息与电气工程学院，上海 200240；4.广东省新能源电力系统智能运行与控制企业重点实验室，广东 广州 510663；5.中国南方电网公司电网仿真重点实验室，广东 广州 510663）

0 引言

随着“双碳”目标的提出，风／光可再生能源的开发规模、开发区域、开发深度进入了更高的层次［1］。目前，我国西北部规划建设了纵深达数千千米的风光新能源基地，而东南沿海各省每年新开发的海上风电容量已达数万兆瓦［2］，并由近海向深远海快速发展。新能源按资源分布集群开发且多个集群之间广域分布，电网相对薄弱［3］。采用交流系统在广阔区域内汇集波动性功率，其电压稳定性及风光电源的并网稳定性面临技术瓶颈［4-5］。因此，通过柔性直流输电实现新能源基地所在的异步电网互联，汇聚新能源功率并送出的方案受到了广泛的关注［6-8］。

目前，柔性直流输电系统大多采用跟网型控制，通过锁相环检测并网点电压相位［9］，并通过电流矢量控制实现有功／无功功率控制的解耦。在现有控制策略下，柔性直流输电系统所连接的各电网之间相对解耦，若其中一个电网出现频率波动，则其他电网难以为其提供快速频率支撑。为了解决这一问题，一些学者提出通过锁相环检测电网频率，并通过辅助控制回路调节柔性直流输电系统的功率来实现电网频率支撑［10］，但这一策略高度依赖于锁相环。一些研究指出，当换流站接入弱电网时，锁相环的性能会恶化，若参数设置不当，则易诱发稳定性问题，也难以快速准确检测电网频率。

一些学者提出采用构网型控制［11-13］来增强换流器的弱电网运行能力，通过模拟同步发电机的运行方程来实现换流站的自主频率响应。但上述策略大多应用于柔性直流输电系统的恒功率控制端。对于恒电压控制端，若采用虚拟同步控制，则会使其功率调节速度变慢，难以维持直流电压的稳定。文献［14］提出的惯性同步控制能同时实现恒电压控制端的电网自同步控制，但其所提供的支撑功率仅从直流电容中提取，对电网的支撑效果较弱。

为此，本文提出了柔性直流输电系统的双端构网型控制策略，主要创新点如下：①将柔性直流输电换流器的直流侧电容等效为同步电机转子，使两侧换流器分别模拟同步发电机、同步电动机运行，有效提高了换流器的弱电网运行能力；②将直流线路等效为连轴，且通过设置直流电压-有功功率下垂系数，增加该连轴的等效阻尼，维持直流电压的稳定，并实现有功功率的灵活控制；③设计了柔性直流输电换流器的电网频率响应策略，在电网频率发生变化时，增大换流器的等效惯性与阻尼，实现对电网的主动频率支撑；④设计了柔性直流输电换流器的电网故障穿越策略，通过电流内环限制故障电流，通过增大等效惯性与阻尼来避免功角失稳，通过将非故障端的功率给定置0来避免直流系统过压或欠压。

1 整体控制结构

2 直流电压-有功功率自同步控制

2.1 直流电压自同步控制

对于柔性直流输电换流器而言，其直流电压幅值Udc与其两侧功率相关，如式（1）所示。

式中：ΔUdc为直流电压的变化量；Ceq为直流侧等效电容，对于两电平换流器，Ceq为直流侧滤波电容，而对于模块化多电平换流器（modular multi-level converter，MMC），Ceq为子模块在直流侧的等效电容；Pdc为直流侧输入功率；Pac为交流侧输出功率；Udc0为直流电压的稳态工作点。这一特性与式（2）所示同步电机的转子运动方程类似。

式中：Δωm为转子转速的变化量；J为同步电机的转动惯量；ωm0为转子转速的稳态工作点；Pm为机械功率；Pe为并网电功率。可以发现，直流电压与同步发电机的转子转速、电容大小以及同步电机的转子转动惯量具有对应关系。

为了进一步模拟同步电机转子转速与输出频率之间的比例关系，可以将直流电压与输出交流频率通过式（3）联系起来，即检测换流器的直流电压Udc，根据式（3）计算换流器的输出频率fc。

式中：K为耦合系数；Udcref为直流电压的给定值；f0为电网的额定频率，值为50 Hz。假设柔性直流输电换流器通过一个电抗与无穷大电源相连，此时换流器的输出功率Pac为：

式中：Uc为换流器输出的交流电压；Ug为电网等效无穷大母线电压；X为电网的等效电抗；fg为电网频率；δ为换流器的功角。由式（4）可知，若换流器的输出频率大于电网频率，则会导致换流器的功角δ增大，从而增大换流器的输出功率Pac。由式（1）可知，Pac增大会导致直流电压Udc降低。由式（3）可知，直流电压Udc降低会导致换流器的输出频率下降，并最终与电网频率保持同步，这一同步过程与同步电机较为类似。在工作点附近线性化，可以列写柔性直流输电换流器与同步电机类似的同步方程，如式（5）所示。

式中：Δfc为换流器输出频率的变化量；Hv为等效惯性时间常数。与同步发电机转子类似，当电网频率变化幅度不大（一般电网频率不超出（50±0.5）Hz）时，换流器的直流电压也将维持在给定值附近，此时换流器工作在恒直流电压控制模式。

若柔性直流输电系统两侧的换流器均采用上述同步策略，假设Udcref、K等控制参数一致，则此时直流侧输入功率Pdc可表示为：

式中：R为直流线路电阻。假设当Pdc为正值时，换流器2为功率送端换流器，换流器1为功率受端换流器。由式（6）可知，无论是送端电网还是受端电网发生频率变化，该频率变化将直接反映在直流电压上，从而影响直流系统的传输功率，且直流功率的变化方向与送端电网的频率变化方向相同，与受端电网的频率变化方向相反。这一特性能实现送端电网与受端电网的双向频率支撑。举例说明如下：若送端电网发生频率跌落，则直流传输功率变小，即送端电网流出的有功功率变小，从而阻尼送端电网的频率下降；若受端电网发生频率跌落，则直流传输功率变大，流入受端电网的有功功率变大，从而能支撑受端电网的频率。此时2个电网类似于被同步电动机-连轴-同步发电机系统相连，功率送端换流器可等效为同步电动机，而功率受端换流器可等效为同步发电机，直流线路可等效为连轴，如图2所示。图中：Pac1、Pac2分别为换流器1、2 的交流侧输出功率；Leq为直流侧等效电感；ωm1、ωm2分别为同步发电机、同步电动机的转子转速；Pe1、Pe2分别为同步发电机、同步电动机的并网电功率；fe1、fe2分别为同步发电机、同步电动机的电频率。

2.2 直流电压-有功功率下垂控制

2.1节利用直流电容的动力学特性，构建了柔性直流输电换流器的自同步机制，但当柔性直流输电系统的双端换流器均采用2.1 节所述的自同步控制策略时，会出现两方面的问题：①缺乏阻尼，使电网同步过程变长，且容易出现振荡；②由式（6）可以发现，柔性直流输电系统的直流侧输入功率Pdc仅与两侧频率相关，无法自由控制。因此，本文在2.1 节所述直流电容电压同步的基础上，引入了Pdc-Udc下垂控制环节，一方面可以为同步过程增加阻尼，另一方面也能够实现对Pdc的自由控制。

若两端换流器同时采用2.1 节所述自同步控制策略，则柔性直流输电系统的直流侧输入功率Pdc（功率方向以换流器2流向换流器1为正）可表示为：

可见，通过合理设置两端换流器的功率给定值，即可实现对柔性直流输电系统传输功率的稳定控制。

此外，通过设置下垂控制环节还能为柔性直流输电换流器的电网同步过程增加阻尼，加快同步速度并增强同步稳定性，将式（9）代入式（7），可得：

式中：Pdc0为直流系统传输功率的稳态工作点；ΔPdc为直流功率的变化量；Δfc1、Δfc2分别为换流器1、2输出频率的变化量。

由式（14）可知，柔性直流输电系统传输的功率将随着换流器的输出频率发生变化，以换流器1 的同步过程为例，假设此时电网2的频率不变，可得：

式中：变量上标“′”表示标幺值；D′v1、H′v1分别为换流器1 阻尼系数、虚拟惯性系数的标幺值；Pnom为额定有功功率；Ceq1为换流器1 的等效直流电容。可发现，式（16）中的D′v1Δf′c1与同步发电机同步方程中的阻尼项类似，其能加快同步速度，改善同步稳定性。

3 电网频率支撑策略

将式（16）代入式（5）中，可以得到换流器1 的同步方程为：

式中：G1(s)为换流器输出频率变化量与电网频率变化量间的传递函数；Hv1为换流器1 的虚拟惯量；Δf′g1为电网1 频率变化量的标幺值；X′Σ1为等效电网阻抗的标幺值。稳态时，G1(s)≈1，即换流器输出频率与电网频率保持相同。由式（14）可知，当换流器的输出频率发生变化时，会引起直流侧输入功率的变化，因此电网频率变化会引起直流侧输入功率的变化。以换流器1 为例，假设电网2 的频率保持不变，电网1的频率变化量为Δfg1，将式（17）代入式（15），有：

因此，当任一电网频率发生变化时，直流侧输入功率也会发生变化，且功率变化方向与电网频率变化方向相反，功率变化量与电网频率变化量成正比，这一特性与一次调频比较类似。由式（18）可知，K1越大，对电网的频率支撑能力越强。但由式（16）和式（17）可知，K1增大会使换流器的功角调节速度变慢，导致稳态下的有功功率调节速度变慢。在两侧换流器的K（K1、K2）值都取得很大的情况下，容易引起直流电压波动。因此，本文在常态下设置K1、K2值都较小（1～5 左右），而在某一电网的频率发生变化后，将该电网侧换流器的K值增大（10～20 左右），实现暂态下的频率支撑，且在电网频率恢复后，再将K值恢复为原本的大小。

4 电网故障穿越策略

由于交流电网大多采用架空线传输，接地故障较为常见［15］。本文从电流限幅、功角限制、功率平衡3 个方面设计了新型控制策略下换流器的电网故障穿越策略，使柔性直流输电系统能够安全稳定地穿越电网低电压故障。

4.1 电流限幅策略

由于电力电子换流器的过流能力有限，需要对换流器的输出电流进行限制。考虑到MMC 交流侧无滤波电容特性下交流电压-交流电流双闭环控制性能不佳的问题［16-18］，本文采用文献［19］中提出的虚拟导纳+环形限幅器+电流内环结合的策略对电流进行限幅，控制框图如图3所示。

通过限幅环节后，获得电流的最终参考值i*d、i*q，再通过电流内环获取换流器输出交流电压的调制波，该部分与常规电流内环控制相同，不再赘述。

4.2 功角限制策略

换流器的同步方式模拟了同步电机，因此同样存在功角稳定性问题［20］，且由于常态下换流器的惯性时间常数Hv和阻尼系数Dv较小，在电网发生严重故障时，换流器的输入／输出功率受限，由式（16）可知，此时换流器的频率会快速变化，容易导致功角越过稳定极限，因此在电网故障下需要对换流器的频率和功角变化速度进行限制。本文采取的限制方法是在电网发生故障时快速增大故障端换流器的耦合系数K，将其值增大为稳态值的数百倍。由式（16）可知，此时故障端换流器的输出频率基本不会变化，能够有效避免故障端换流器的功角失稳。在这个过程中，非故障端换流器的耦合系数K不变，由非故障端换流器维持直流电压稳定。

4.3 功率平衡策略

电网发生短路故障会导致故障端换流器的输入或输出功率迅速下降，若此时不能快速地减小非故障端换流器的输入或输出功率，则容易导致直流系统的过电压或欠电压保护动作。因此，本文在两侧换流器的功率给定值上加入滞环控制。对于功率送端，当直流电压超过1.05 p.u.时，将有功功率给定值Pref置0，直到直流电压低于1.01 p.u.时再恢复至原有功率给定值。对于功率受端，当直流电压低于0.95 p.u.时，将有功功率给定值Pref置0，直到直流电压高于0.99 p.u.时再恢复至原有功率给定值。通过这一设置能够在电网发生故障时使柔性直流输电系统不出现过压或欠压问题。

5 仿真分析与验证

根据图1，在PSCAD／EMTDC 软件中构建仿真模型，模型的电气参数与控制参数分别如附录A 表A1和表A2所示。

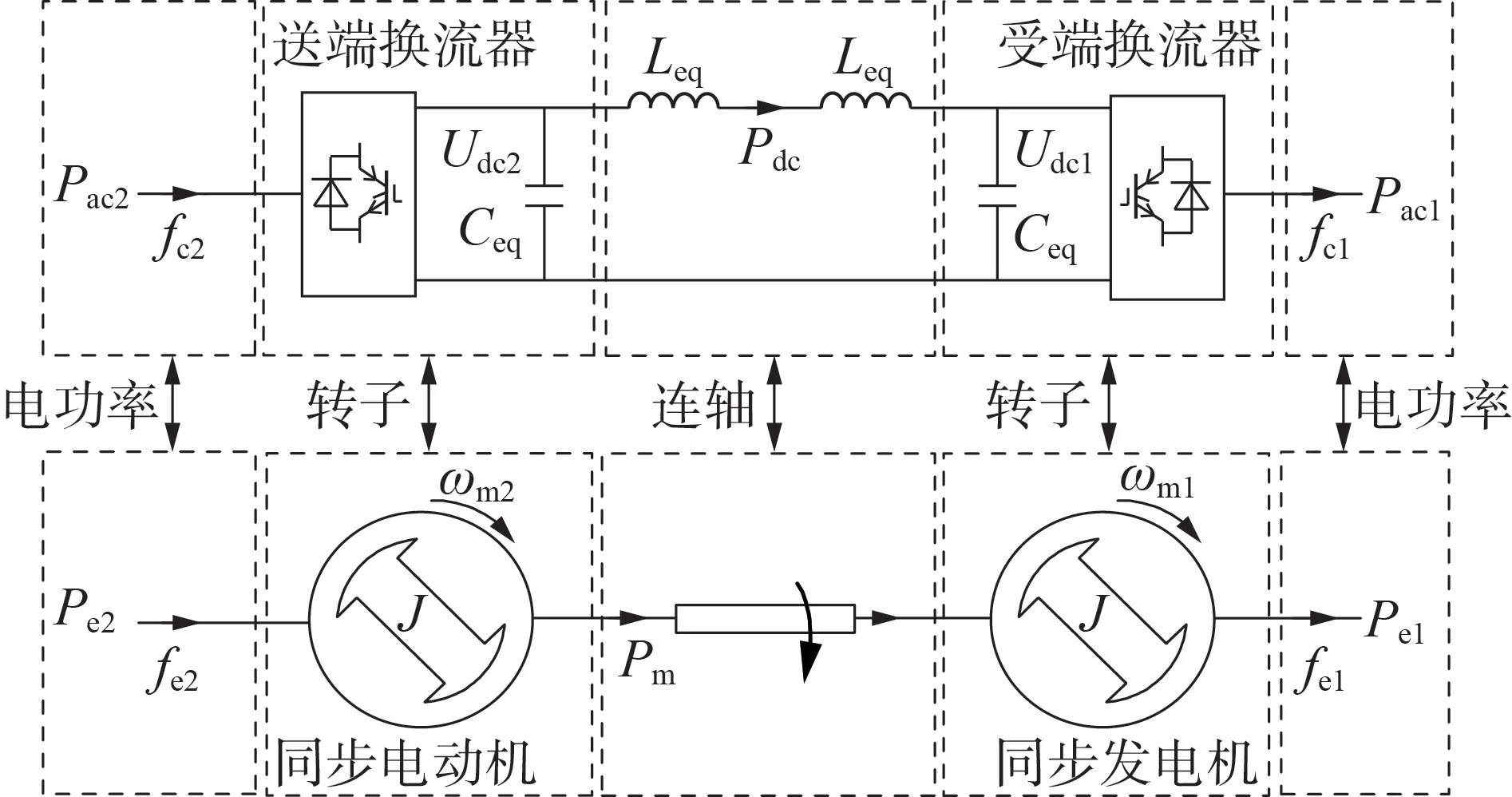
图2 换流器-同步电机等效示意图Fig.2 Equivalent diagram of convertersynchronous machine

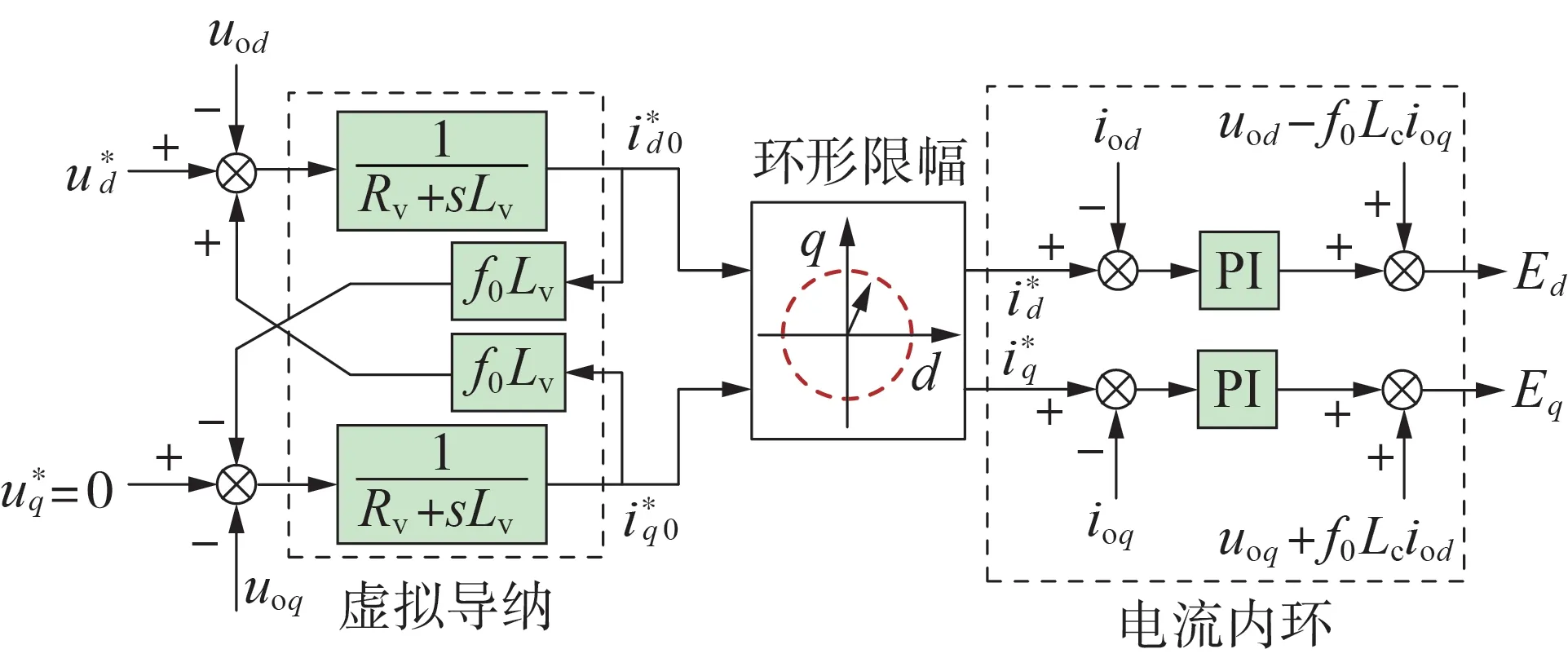
图3 虚拟导纳+电流内环的限流策略控制框图Fig.3 Current limiting strategy control block diagram of virtual admittance+current inner loop

5.1 电网适应性验证

为了验证本文所提控制策略的电网适应性与弱电网运行能力，将换流器1接入点的短路比ξSCR设置为10，在3 s 时将短路比从10 减小为5，在6 s 时再次减小为2.5。当采用传统跟网型控制策略与本文所提控制策略时，换流器1 的有功功率响应如图4 所示。由图可知：当采用传统跟网型控制策略时，换流器在强电网运行条件下能够稳定运行，但当电网短路比减小后（弱电网运行条件下），易出现振荡失稳；而当采用本文所提控制策略时，换流器在不同的电网强度下均具备良好的运行性能。

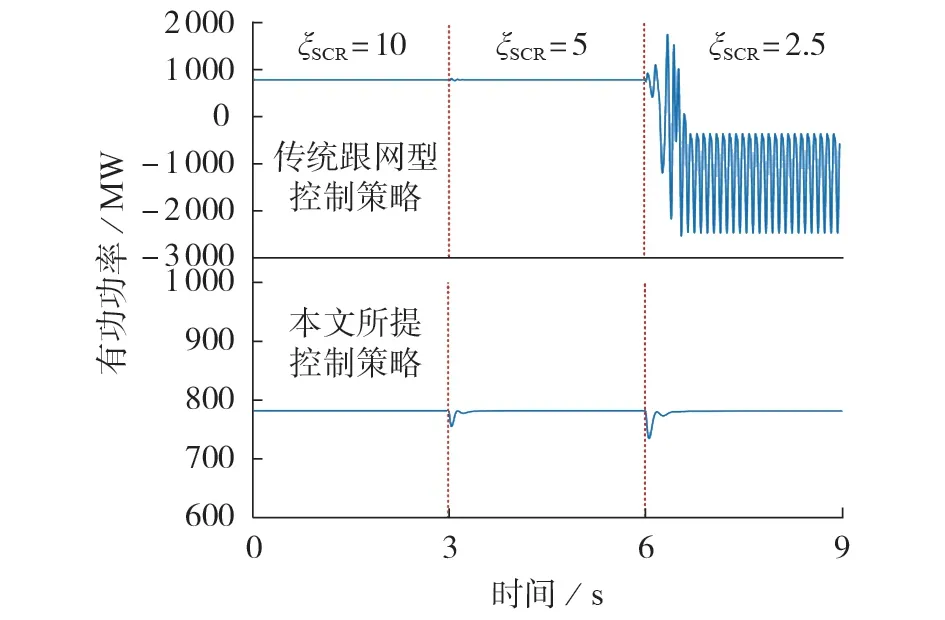
图4 换流器1的有功功率响应Fig.4 Active power response of Converter 1

5.2 功率调节能力验证

设置直流功率给定值Pref为800 MW，且Pref1=-Pref2=Pref。2 s 时将Pref改为-800 MW，并在5 s 时将Pref恢复为800 MW，本文所提控制策略下的换流器有功功率（以直流侧流向交流侧的功率为正，后同）和直流电压如图5 所示。由图可知，在本文所提控制策略下，柔性直流输电系统两端的换流器具备快速功率控制能力，并且在潮流反转、有功功率突变的情况下能够稳定控制直流电压。

图5 换流器有功功率和直流电压Fig.5 Active power of converters and DC voltage

5.3 频率支撑能力验证

为了验证本文所提控制策略的频率支撑能力，将换流器1 交流侧接入10 GW 同步发电机与6 GW负荷组成的等值系统。在2 s时负荷突增2 GW，无频率支撑、有频率支撑2种情况下的电网频率变化结果见图6。可知，在有频率支撑的情况下，当换流器1接入的电网频率下降后，柔性直流输电系统传输的功率变大，使换流器1 输出的有功功率上升，相比无主动频率支撑的情况，其能有效减慢电网的频率下降速度，改善频率最低点，且该频率支撑为完全自发响应，无需额外控制，响应速度和实时性良好。

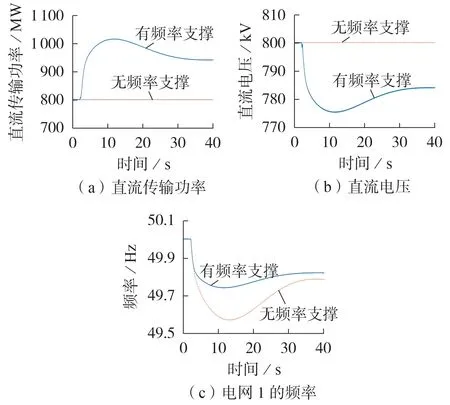
图6 频率支撑能力验证仿真结果Fig.6 Simulative results of frequency support capability verification

5.4 故障穿越能力验证

为了验证本文所提控制策略的故障穿越能力，将直流功率给定值设置为800 MW，换流器1 为功率受端，换流器2 为功率送端，分别在功率受端电网发生故障、功率送端电网发生故障2种工况下进行仿真。

1）工况1：功率受端电网发生故障。

在2 s 时，功率受端电网发生三相短路接地故障，故障期间换流器1 的并网点交流电压下降至额定值的30 % 左右，仿真结果见图7。由图可知，当功率受端电网发生三相接地短路故障后，换流器1 能通过电流内环快速限制短路电流大小，避免损坏换流器。同时，换流器1 与换流器2 协同配合，快速降低直流功率，避免直流系统过压。故障过程中，由于换流器的电压源特性，换流器1 还能自发输出无功功率支撑电网电压恢复。故障结束后，换流器1 能够迅速恢复正常运行，不会出现功角稳定性问题。

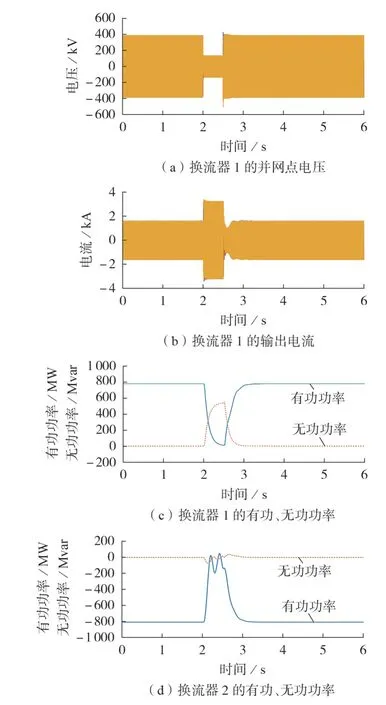
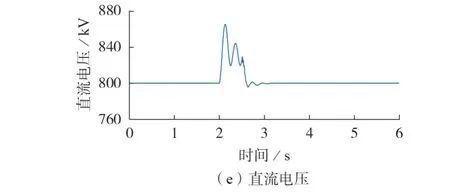
图7 工况1的故障穿越仿真结果Fig.7 Simulative results of fault ride-through under Working Condition 1

2）工况2：功率送端电网发生故障。

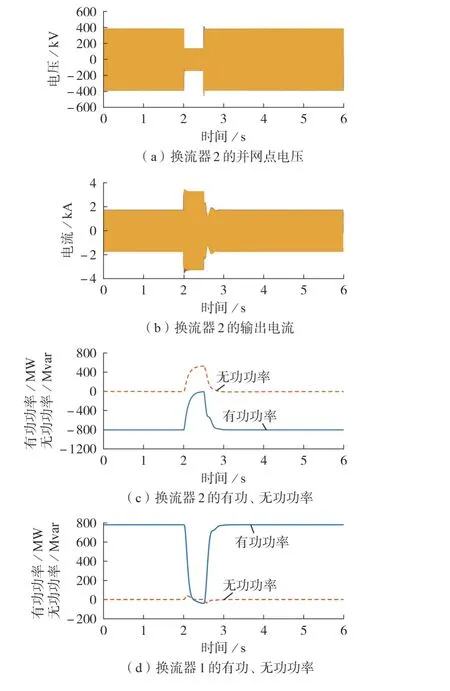
在2 s 时，功率送端电网发生三相短路接地故障，故障期间换流器2 的并网点交流电压下降至额定值的30 % 左右，仿真结果如图8所示。

book=208,ebook=214

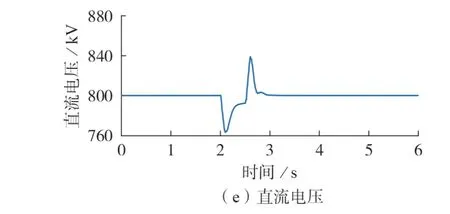
图8 工况2的故障穿越仿真结果Fig.8 Simulative results of fault ride-through under Working Condition 2

由图8 可知，当功率送端电网发生三相接地短路故障后，换流器2 能通过电流内环快速限制短路电流大小，避免损坏换流器。同时，换流器1 与换流器2 协同配合，快速降低直流功率，避免直流系统欠压。故障过程中，由于换流器的电压源特性，换流器2 还能自发输出无功功率支撑电网电压恢复。故障结束后，换流器2 能够迅速恢复正常运行，不会出现功角稳定性问题。

6 结论

为了解决传统控制策略下柔性直流输电系统弱电网运行性能差、无法主动支撑电网的问题，本文提出了一种用于异步弱电网互联的柔性直流输电系统的双端构网型控制策略，使柔性直流输电系统两端的换流器能够不经锁相环自主同步电网，提高了柔性直流输电系统的弱电网接入能力。在该策略下，柔性直流输电系统的双端电网均体现为电压源特性，能够有效地支撑弱电网稳定运行：当电网发生负荷突变时，柔性直流输电系统能自动响应功率缺额，调节所传输的有功功率，参与频率调节，提供主动频率支撑；当电网发生短路故障时，换流器能在保证自身安全稳定穿越的前提下，主动输出无功功率，提供主动电压支撑。最后，基于PSCAD／EMTDC 软件进行算例仿真，结果验证了所提控制策略的有效性。

附录见本刊网络版（http：//www.epae.cn）。