含混合多端直流的电力系统静态电压稳定域构建

2023-09-11陈厚合李国庆

电力自动化设备 2023年9期

李雪，崔悦，姜涛，陈厚合，李国庆

（东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林吉林 132012）

0 引言

基于传统电网换相换流器的直流输电（line commutated converter based high voltage direct current transmission，LCC-HVDC）技术具有传输容量大、输电距离远、工程造价低等优点［1］，已在实际工程中得到广泛应用［2］，但LCC-HVDC 存在换相失败的风险；而基于电压源换流器的直流输电（voltage source converter based high voltage direct current transmission，VSC-HVDC）技术以其有功功率和无功功率独立控制、不存在换相失败且对交流系统强度要求低等优点，受到电网运行和研究人员关注［3］，但VSC-HVDC 传输容量较小，投资成本较高。而由LCC-HVDC 和VSC-HVDC 构成的混合多端直流输电（hybrid multi-terminal direct current transmission，Hybrid-MTDC）技术能充分发挥LCC-HVDC 和VSCHVDC 各自优势，在避免换相失败和实现功率大容量输送的基础上，实现直流输电的灵活控制［4-5］，是优化资源配置和实现风电与光伏大规模消纳的重要技术手段［6］。随着Hybrid-MTDC 工程数量日益增多，交直流系统耦合程度不断增强，Hybrid-MTDC 控制策略也会影响到交流系统静态电压稳定性［7］，加剧了含Hybrid-MTDC 的交直流系统运行风险。故研究含Hybrid-MTDC 的交直流系统电压稳定性具有重要工程意义。

目前，国内外学者已对交直流系统静态电压稳定性分析开展了大量研究，主要方法有连续潮流（continuation power flow，CPF）法、灵敏度指标法、短路比等［8-9］。文献［10］在LCC-HVDC 中计及换流器控制策略对静态电压稳定性的影响，提出了一种评估交直流系统静态电压稳定裕度的综合短路比强度指标；文献［11］提出可衡量系统强度的广义短路比指标，以评估交直流系统的静态电压稳定性；文献［12］根据雅可比矩阵奇异值灵敏度指标，提出一种增加交直流系统静态电压稳定裕度的直流换流站控制策略；文献［13］分析了电压源换流器多端直流（voltage source converter based multi-terminal direct current，VSC-MTDC）系统的换流站控制参数对系统负荷裕度的影响，借助有功和无功功率控制参数对电压稳定的轨迹灵敏度，提出一种改善交直流系统电压稳定性的VSC-MTDC调控策略。上述方法在研究交直流系统的静态电压稳定性中已发挥重要作用，但其均是确定性方法，难以有效计及负荷和新能源出力不确定性对交直流系统电压稳定性的影响。为此，文献［14］计及负荷静特性构建含大规模风电的交直流系统静态电压稳定域（static voltage stability region，SVSR），以研究直流系统控制策略、负荷静特性、风电出力对交直流系统静态电压稳定性的影响；文献［15］提出一种计及VSC-MTDC 控制策略的交直流系统SVSR构建方法。

上述文献仅适用于含单一类型换流站（如LCC换流站或VSC 换流站）的交直流系统静态电压稳定性分析和SVSR 的构建，目前针对含混合类型换流站（LCC-VSC换流站）的交直流系统静态电压稳定性分析与评估鲜有研究。随着Hybrid-MTDC 技术的不断发展及其在实际工程中的广泛应用，亟待针对含Hybrid-MTDC 的交直流系统SVSR 构建进行深入研究。

含Hybrid-MTDC 的交直流系统换流站类型多样、控制策略复杂多变，并且多座LCC 换流站和VSC换流站间控制策略的协同机制更为复杂。为此，本文同时计及多座换流站之间控制策略协同配合对SVSR的影响。从实际工程需求出发，提出了一种含Hybrid-MTDC 的交直流系统静态电压稳定域边界（static voltage stability region boundary，SVSRB）快速搜索的预测-校正方法，以更真实、准确地实现含Hybrid-MTDC 的交直流系统SVSR 构建。该方法首先通过所提含Hybrid-MTDC的CPF模型搜索SVSRB上首个临界点；进而根据含Hybrid-MTDC 的交直流系统SVSRB 的边界拓扑特性，计及Hybrid-MTDC 中多类型换流站控制策略的转换，提出一种含Hybrid-MTDC的交直流系统SVSRB搜索预测-校正模型，由所得首个临界点实现含Hybrid-MTDC 的交直流系统SVSRB准确、快速搜索；最后通过含Hybrid-MTDC的IEEE 5 节点测试系统和IEEE 118 节点测试系统对所提含Hybrid-MTDC 的交直流系统SVSR 构建方法进行分析、验证。

1 含Hybrid-MTDC 的交直流系统基态潮流求解

典型的Hybrid-MTDC包含LCC和VSC 2类换流站，由于二者结构与工作原理不同，下面分别介绍这2 类换流站的接口模型、控制策略及节点等效类型，并给出了含Hybrid-MTDC 的交直流系统潮流求解方法。

1.1 换流站控制策略及等效节点类型

典型的VSC换流站和LCC换流站的拓扑结构分别见附录A 图A1、A2，VSC 换流站和LCC 换流站的接口模型分别见式（A1）—（A3）和式（A4）—（A7）。当LCC 换流站与VSC 换流站采用不同控制策略时，与其相连的交直流侧节点将根据换流站的不同控制策略等效为不同类型的节点，其控制策略与等效节点类型之间关系见表1。

表1 各换流站控制策略与等效节点类型Table 1 Control strategies of converter stations and equivalent bus types

1.2 不同控制策略下换流站向交流系统注入的功率

由表1 可知，当换流站运行于不同控制策略时，其向交流系统注入的有功功率和无功功率都将发生变化，这将影响交流系统的潮流分布及其静态电压稳定性。在表1 所示的不同类型换流站及其控制策略下，各类型换流站向交流系统注入有功功率和无功功率的计算过程见附录B式（B1）—（B7）。

当VSC 换流站运行于表1 所示的不同控制策略时，其向交流系统注入的有功功率Psv为：

式中：Rl为LCC 换流站换相电阻；Pdcl为LCC 换流站直流侧有功功率；Icl为LCC 换流站交流侧电流；Pl，loss为LCC换流站功率损耗。

对应地，不同控制策略下LCC 换流站向交流系统注入的无功功率Qsl为：

式中：Pcl为LCC换流站交流侧有功功率；Xl为LCC换流站换相电抗；φ为LCC换流站功率因数角。

1.3 含Hybrid-MTDC的交直流系统潮流求解

目前，交直流系统潮流求解方法主要为交替迭代法和统一求解法［16］，交替迭代法对交流系统潮流和直流电网潮流分别求解，具有灵活性好、效率高的特点，能够方便实现交直流控制策略的灵活转换。为此本节提出一种含Hybrid-MTDC 的交直流系统潮流求解的交替迭代法，其求解模型主要包括交流系统的潮流计算模型、直流系统的潮流计算模型以及LCC与VSC换流站信息交互模型。

交流系统包括纯交流节点和公共耦合点（point of common coupling，PCC）。纯交流节点的潮流方程为：

式中：x为交流系统待求解状态变量向量。对于纯交流节点i，式（6）的具体表达式为：

式中：Pk与Qk分别为PCC 节点k注入的有功功率与无功功率；Ps，k与Qs，k分别为换流站向交流系统中PCC节点k注入的有功功率与无功功率。

直流系统潮流方程为：

式中：v为直流系统待求解状态变量向量。对于直流节点m，其式（10）的具体表达式为：

式中：Pdcm为直流节点m的有功功率；Udcm为直流节点m的电压；Gdcmn为直流节点m与直流节点n之间电导；M为直流系统的节点数，本文中M=3；p为直流电网输电极对数，本文中p=2。

根据式（A1）—（A7）所示VSC 换流站和LCC 换流站接口模型，可得含Hybrid-MTDC 的交直流系统潮流求解的交替迭代法计算流程如附录B 图B1 所示，具体步骤如下。

1）进行交流系统的潮流计算。根据换流站设定的控制策略，确定PCC的等效节点类型与注入功率，并通过迭代过程A 求解交流系统的潮流结果，即交流系统各节点的电压幅值Us、相角θs、注入的有功功率Ps和无功功率Qs。

2）进行“交流向直流”的信息交互过程A。根据换流站接口模型，依据PCC处电压和注入功率，计算换流站损耗Ploss和换流站向直流系统注入的有功功率Pdc。

3）进行直流系统的潮流计算。依据直流系统各节点有功功率Pdc，通过迭代过程B 求解直流系统的潮流结果，即直流系统各节点电压Udc和有功功率Pdc。

4）进行“直流向交流”的信息交互过程B。根据换流站接口模型，计算换流站注入交流PCC 节点k的新的有功功率Pnews，k。

5）利用Pnews，k计算交流系统与直流系统之间的功率不平衡量。若不平衡量大于设定阈值，则继续进行交流系统的潮流计算；若不平衡量小于或等于设定阈值，则输出交直流系统的潮流计算结果。

2 SVSRB搜索

SVSR 描述的是电力系统功率注入空间内，在确定网络结构下，能够维持系统静态电压稳定的运行点集合。在实际电力系统SVSR 构建过程中可将SVSR 构建问题转换为对SVSRB 的搜索问题，由文献［17-19］可知：电力系统SVSRB 是由鞍结分岔（saddle node bifurcation，SNB）点与极限诱导分岔（limit induced bifurcation，LIB）点构成，本文主要关注由SNB 点构成的SVSRB，其表达式如式（12）所示［20-23］。

文献［19］提出了一种交流系统SVSRB 快速搜索的预测-校正方法，但其仅适用于交流系统。为此，本文提出了一种适用于含Hybrid-MTDC 的交直流系统的SVSR 快速构建方法，可实现式（12）所示的电力系统的SVSRB快速搜索。

3 含Hybrid-MTDC 的交直流系统SVSRB 快速搜索方法

计及多类型换流站控制策略转换，下面提出一种含Hybrid-MTDC 的交直流系统SVSRB 的快速搜索方法。

3.1 含Hybrid-MTDC的交直流系统初始SNB点求解

采用预测-校正方法搜索电力系统SVSRB 时，需首先确定SVSRB 上某一SNB 点，进而再根据含Hybrid-MTDC 的交直流系统SVSRB 拓扑特性，采用预测-校正方法搜索SVSRB。为此，本节首先提出一种计及多类型换流站控制策略转换的CPF 模型，以搜索含Hybrid-MTDC 的交直流系统SNB 点。该CPF模型为：

式中：bac为交流系统功率增长方向；Ps与Qs分别为换流站向交流系统中PCC注入的有功功率与无功功率向量；λ为功率增长系数。

由1.2 节可知，当换流站控制策略转换时，换流站向交流系统注入的功率将发生改变，因此采用式（13）所示CPF 模型搜索系统的SNB 点时，需根据系统运行参数变化转换换流站控制策略，各换流站控制策略转换依据如下。

1）VSC 换流站控制策略转换依据。VSC 换流站可实现有功功率和无功功率的独立控制，其交流侧控制策略转换依据是预防VSC 换流站电压Ucv越限，直流侧控制策略将根据VSC换流站向交流系统注入的有功功率Psv在各控制策略中进行相互转换。

2）LCC 换流站控制策略转换依据。为预防LCC换流站直流电流Idcl和触发角θ越限，LCC 换流站控制策略将根据其向交流系统注入的有功功率Psl在各控制策略间进行相互转换。

3.2 含Hybrid-MTDC 的交直流系统SVSRB 快速搜索的预测-校正算法

采用3.1 节所提CPF 模型搜索含Hybrid-MTDC的交直流系统的首个SNB 点后，计及多类型换流站控制策略转换对SVSRB 的影响，本文提出了一种含Hybrid-MTDC 的交直流系统SVSRB 快速搜索的预测-校正模型，如式（14）所示。

参考文献［19］，采用式（14）所提预测-校正模型搜索含Hybrid-MTDC 的交直流系统SVSRB 的算法流程见附录C。

3.3 含Hybrid-MTDC 的交直流系统换流站控制策略转换方案

以图1 所示的我国南方某个含Hybrid-MTDC 的实际交直流系统为例，说明采用本文所提含Hybrid-MTDC 的交直流系统SVSRB 快速搜索方法时，不同类型换流站的控制策略转换方案。由图可知：LCC换流站处于整流侧，VSC1、VSC2换流站均在逆变侧。根据LCC换流站与VSC换流站各自控制策略转换依据，搜索含Hybrid-MTDC 的交直流系统SVSRB 时各换流站的控制策略转换方案如下。

图1 含Hybrid-MTDC的交直流系统拓扑结构Fig.1 Topology structure of AC／DC system with Hybrid-MTDC

随着负荷连续变化，PCC有功增量ΔPPCC为：

式中：bPCC为PCC 处的功率增长方向。由式（15）可知，换流站以及直流系统的存在使得交流系统PCC处的有功增量还包含换流站向交流系统注入的有功功率。当LCC 与VSC 换流站处于不同的初始状态时，可根据以下3 种方案进行直流侧换流站控制策略转换。

3.3.1 控制策略转换方案1

控制策略转换方案1示意图见附录D图D1。当LCC 换流站采用定有功功率控制时，随着LCC 换流站直流母线电压降低，为避免维持LCC 换流站有功功率恒定而导致LCC 换流站电流超越其上限，需将其控制策略由定有功功率控制转换为定直流电流控制；同时由于直流线路的电压降落，VSC 换流站直流侧电压有可能低于其下限，不同初始状态下VSC 换流站的控制策略转换方案设置如下。

1）初始状态1，VSC1换流站采用定有功功率控制，VSC2换流站处于下垂控制。由于VSC1换流站直流侧电压越限，其将转换为定直流电压控制；为保证直流系统潮流平衡，VSC2换流站仍保持下垂控制不变。

2）初始状态2，VSC1换流站采用定直流电压控制，VSC2换流站采用定有功功率控制。由于直流侧电压达到限值，VSC1换流站保持定直流电压控制不变；由于VSC2换流站直流侧电压越限且VSC1换流站采用定直流电压控制，则VSC2换流站将由定有功功率控制转换为下垂控制。

3）初始状态3，VSC1、VSC2换流站均处于下垂控制。为维持直流系统潮流平衡，VSC1、VSC2换流站均维持下垂控制不变。

在所提SVSRB 快速求解的预测-校正算法中，各换流站的控制策略会在每一个SNB 点的预测、校正阶段进行参数越限判断，进而进行控制策略转换，直流侧的功率方程也将相应改变，直流侧功率的变化会影响式（13）中Ps，即LCC 换流站和VSC 换流站向交流系统注入的有功功率。在初始状态1、2 下，控制策略转换方案1 中各换流站的直流功率方程分别为：

式中：Pdc1、Pdcv1、Pdcv2分别为LCC、VSC1、VSC2换流站注入的直流功率；k1为VSC 换流站下垂系数；Idcl（set）为LCC 换流站直流电流设定值；Idcv1为VSC1换流站直流侧电流；Udcl与Udcv2分别为LCC换流站与VSC2换流站直流侧电压；Udcv1（set）为VSC1换流站直流侧电压设定值；Udcv0，2为VSC2换流站下垂控制直流侧电压设定值。

在初始状态3下，控制策略转换方案1中各换流站的直流功率方程分别为：

式中：Udcv1为VSC1换流站直流侧电压；Udcv0，1为VSC1换流站下垂控制直流侧电压设定值。

3.3.2 控制策略转换方案2

控制策略转换方案2示意图见附录D图D2。随着直流电网传输功率不断增加，LCC 换流站触发角将逐渐减小，进而导致LCC 换流站触发角低于其下限，此时应将其控制策略转换为定最小触发角控制，不同初始状态下各VSC换流站的控制策略转换方案设置如下。

1）初始状态1，VSC1、VSC2换流站均采用下垂控制。由于VSC1、VSC2换流站向交流系统注入的有功功率高于采用定有功功率控制时的有功设定值，为兼顾直流系统潮流平衡及增大静态电压稳定性，VSC1、VSC2换流站采用下垂控制不变。

2）初始状态2，VSC1换流站采用下垂控制，VSC2换流站采用定直流电压控制。为增大静态电压稳定裕度，VSC1换流站控制策略保持下垂控制不变；VSC2换流站采用定直流电压控制将导致VSC1换流站直流侧电压越限，此时需将VSC2换流站控制策略转换为下垂控制。

控制策略转换方案2 中各换流站的直流功率方程为：

式中：cosθ（set）为LCC 换流站最小控制角余弦值；Kt为换流变变比；nt为每极含6 脉动换流器个数；Usl为LCC换流站交流侧电压；Idcl为LCC换流站直流电流。

3.3.3 控制策略转换方案3

控制策略转换方案3示意图见附录D图D3。当LCC 换流站采用定有功功率控制时直流侧电压越限，而VSC换流站未采用定直流电压控制时，LCC 换流站将转换为定直流电压控制。不同初始状态下各VSC换流站控制策略转换方案设置如下。

1）初始状态1，VSC1换流站采用定有功功率控制，VSC2换流站采用下垂控制。VSC1换流站对应直流节点电压幅值越限，但LCC 换流站已采用定直流电压控制，此时需将VSC1换流站控制策略转化为下垂控制；VSC2换流站下垂控制保持不变。

2）初始状态2，VSC1、VSC2换流站均为下垂控制。由于LCC 换流站已采用定直流电压控制，因此VSC1、VSC2换流站将继续维持当前下垂控制不变。

控制策略转换方案3 中各换流站的直流功率方程为：

由于VSC 换流站交流侧均独立控制，各换流站交流侧控制策略不会相互影响，其控制策略转换方案推导过程见附录E。

综上，计及多类型换流站的控制策略切换特性和站间控制策略协同，采用本文所提预测-校正方法在二维注入空间中搜索含Hybrid-MTDC 的交直流系统SVSRB的计算步骤见附录F。

3.4 三维SVSRB搜索

本节进一步以式（14）所提二维SVSRB 搜索模型为基础，推导出含Hybrid-MTDC 的交直流系统三维SVSRB搜索模型，如式（20）所示。

进一步以附录F 所提含Hybrid-MTDC 的交直流系统二维SVSRB 搜索方法为基础，采用式（20）所提三维SVSRB 搜索模型，在三维注入空间内，搜索含Hybrid-MTDC 的交直流系统SVSRB 的示意图如图2所示，具体步骤见附录G。图中：ΔPλx、ΔPλy、ΔPλz分别为节点x、y、z处的功率增量；ΔPzmax为节点z处的功率增量极限；ΔPz为节点z处的每一层功率增量。

图2 含Hybrid-MTDC交直流系统的三维SVSRB搜索示意图Fig.2 Exploring schematic diagram of three-dimensional SVSRB in AC／DC system with Hybrid-MTDC

4 算例分析

针对所提含Hybrid-MTDC的交直流系统SVSRB快速搜索方法，下面分别通过含Hybrid-MTDC 的IEEE 5 和IEEE 118 节点测试系统算例进行分析，以验证所提方法的准确性与有效性。

4.1 含Hybrid-MTDC的IEEE 5节点测试系统

首先以附录H 图H1 所示含Hybrid-MTDC 的IEEE 5 节点测试系统为例来验证所提含Hybrid-MTDC 的交直流系统SVSRB 构建的准确性，图中直流节点分别经LCC 换流站、VSC1换流站和VSC2换流站与交流系统相连。

4.1.1 二维SVSRB搜索

分别设置2 种场景来搜索二维有功注入空间内含Hybrid-MTDC 的交直流系统SVSRB：①场景1，以负荷有功功率注入为坐标轴；②场景2，以负荷有功功率注入和发电机有功出力为坐标轴。

1）场景1下的搜索过程。

为了维持直流系统电压，本文将LCC 换流站、VSC1换流站和VSC2换流站直流侧初始控制策略分别设置为定有功功率控制、下垂控制与下垂控制。VSC 换流站交流侧初始控制策略分别为定无功功率控制和定交流电压控制，换流站的初始运行参数如附录H表H1所示。

选择负荷节点4、5 作为影响电压稳定性的关键节点，采用所提方法以节点4、5的有功注入为坐标轴搜索交直流系统SVSRB。设CPF模型的预测步长为0.15 p.u.，功率增长方向b0=［0，0，0，0.27，0］T，采用所提CPF 模型搜索SVSRB 上初始SNB 点S1，追踪的PV曲线如图3所示，图中节点电压幅值U4为标幺值。

图3 场景1下节点4的PV曲线Fig.3 PV curve of Bus 4 under Scenario 1

由图3 可知，在负荷连续增加过程中，当系统负荷增加达到7.963 p.u.时，LCC 换流站直流侧电流达到0.452 p.u.，超过了直流侧电流限值0.45 p.u.；VSC1换流站电压Ucv为0.895 p.u.，低于换流站电压Ucv下限值0.9 p.u.。此时LCC 换流站由定有功功率控制转换为定直流电流控制，VSC1换流站交流侧由定无功功率控制转换为定交流电压控制，VSC2换流站直流侧控制策略仍保持下垂控制不变，如图3 中的转换过程1所示。

当系统负荷继续增加到10.350 p.u.时，VSC1换流站交流侧电压为1.108 p.u.，高于其上限值1.1 p.u.，VSC2换流站交流侧电压为0.889 p.u.，低于其下限值0.9 p.u.，此时VSC1换流站由定交流电压控制转换为定无功功率控制，VSC2换流站由定无功功率控制转换为定交流电压控制，如图3 中的转换过程2所示。

继续增加全网负荷，直至系统负荷增加到12.482 p.u.，搜索得到功率增长方向b0上交直流系统的SNB 点S1（0.697，12.482）p.u.。进一步追踪出测试系统未考虑换流站控制策略转换时的PV曲线，对比图3 中是否考虑控制策略转换的系统负荷裕度可知：计及换流站控制策略转换方案后含Hybrid-MTDC的交直流系统的负荷裕度较大，提高了系统的静态电压稳定性。

场景1 下含Hybrid-MTDC 交直流系统的SVSRB如图4 所示，图中ΔPλ4、ΔPλ5均为标幺值。通过所提CPF 模型获得图4 所示的SNB 点S1（0，3.344）p.u.后，根据式（14）所构建的含Hybrid-MTDC 的交直流系统SVSRB 搜索模型，采用所提预测-校正算法搜索SVRSB 上的SNB 点，设SVSRB 预测-校正算法的预测步长为0.4 p.u.，沿功率增长方向b1=［0，0，0，0.26，0.03］T，采用本文所提预测-校正方法，向功率增长方向角δ减少的方向搜索，各换流站PCC 电压等关键参数未越限，控制策略未发生转换，进而搜索到SNB点S2（0.377，3.121）p.u.。

图4 场景1下含Hybrid-MTDC交直流系统的SVSRBFig.4 SVSRB of AC／DC system with Hybrid-MTDC under Scenario 1

以此类推继续沿着功率增长方向角δ减少的方向搜索出SNB 点S3—S9。当在S9基础上继续采用预测-校正方法搜索下一SNB点S10时，由于节点4的电压幅值为1.105 p.u.，超过VSC2换流站交流侧电压幅值上限1.1 p.u.，此时VSC2换流站交流侧由定交流电压控制转换为定无功功率控制，进而最终计算得SNB 点S10处节点4 电压幅值为1.092 p.u.，通过VSC2换流站控制策略的转换使得节点4 电压幅值从越限状态回落到合理电压幅值范围内。继续沿着功率增长方向角δ减少的方向搜索出SNB 点S11、S12，直至δ到达坐标轴边界。对应的各SNB点处各换流站控制策略如表2所示。

表2 场景1下各SNB点处换流站控制策略Table 2 Control strategy of converter station at each SNB under Scenario 1

图4 进一步给出了未考虑各换流站控制策略转换的含Hybrid-MTDC 的交直流系统SVSRB 搜索结果。由表2和图4可知：各换流站采用合理的控制策略转换方案可在含Hybrid-MTDC 的交直流系统参数越限时，及时调整其控制策略，提升含Hybrid-MTDC的交直流系统的静态电压稳定性，扩大含Hybrid-MTDC的交直流系统SVSR。

为了验证所提预测-校正算法搜索的SVSRB 精度，进一步对比采用本文所提SVSRB 预测-校正算法和CPF 算法追踪到的各SNB 点最小特征值，如图5 所示。理论上各SNB 点的最小特征值为0，故计算所得SNB 点最小特征值越接近0，算法计算精度越高。以SNB 点的最小特征值表示算法的计算误差，由图可知：采用本文所提SVSRB 预测-校正算法搜索的SNB 点最大计算误差为1.28×10-2，最小计算误差为3.34×10-3，平均计算误差为9.17×10-3；考虑控制策略转换的CPF 算法搜索的SNB 点最大计算误差为1.59×10-2，最小计算误差为3.34×10-3，平均计算误差为1.07×10-2。这说明本文所提出的算法可以实现含Hybrid-MTDC的交直流系统SVSRB高精度搜索。

图5 场景1下CPF算法与所提SVSRB预测-校正算法求解的SNB点最小特征值Fig.5 Minimum eigenvalue of SNB point calculated by CPF algorithm and proposed SVSRB predictor-corrector algorithm under Scenario 1

2）场景2下的搜索过程。

进一步选择发电机节点2 和负荷节点4 作为影响电压稳定性的关键节点，采用本文所提SVSRB 预测-校正算法在场景2中搜索交直流系统的SVSRB，结果见附录Ⅰ。由附录Ⅰ的结果可知：合理的换流站控制策略不仅能有效防止含Hybrid-MTDC 的交直流系统参数越限，还能将LCC 换流站触发角控制在合理范围内，验证了所提多类型换流站控制策略转换方案的合理性和有效性。

进一步在场景2 下将本文所提SVSRB 预测-校正算法与CPF 算法所得SVSRB 的计算精度进行对比，如图6 所示。由图可知：所提SVSRB 预测-校正算法搜索的SNB 点最大、最小和平均计算误差分别为4.21×10-3、7.4×10-6、2.41×10-3；而CPF 算法搜索的SNB 点最大、最小和平均计算误差分别为6.29×10-3、3.32×10-4、3.41×10-3。再次验证了本文所提方法可实现含Hybrid-MTDC 的交直流系统SVSRB 高精度追踪。

图6 场景2下CPF算法与所提SVSRB预测-校正算法求解的SNB点最小特征值Fig.6 Minimum eigenvalue of SNB point calculated by CPF algorithm and proposed SVSRB predictor-corrector algorithm under Scenario 2

4.1.2 含Hybrid-MTDC 的交直流系统与仅含VSCMTDC的交直流系统SVSRB对比分析

进一步对比场景1、2 中含Hybrid-MTDC 的交直流系统与仅含VSC-MTDC 的交直流系统的SVSR，结果见附录J。含VSC-MTDC 的IEEE 5 节点测试系统数据见文献［15］。由附录J 结果可知：在相同交流系统中，含VSC-MTDC的交直流系统SVSR要远大于含Hybrid-MTDC 的交直流系统SVSR，其原因是VSC换流站较LCC 换流站具有更灵活的调节能力，可独立控制换流站有功功率和无功功率，提高了系统的电压稳定性。

4.1.3 计算效率分析

对比本文所提SVSRB 预测-校正算法与考虑控制策略转换CPF 算法搜索SVSRB 的计算耗时（计算硬件平台CPU Intel Core R5-5500U，主频2.1 GHz，内存8 GB），算例结果见附录K 表K1。由表可知：相对于CPF 算法，本文所提算法的计算效率在场景1中提升了7.70 倍，在场景2 中提升了9.99 倍，可实现含Hybrid-MTDC的交直流系统SVSRB的高效搜索。

4.1.4 预测-校正算法预测步长对计算精度和计算耗时的影响

进一步在场景1、2 中探究本文所提SVSRB 预测-校正算法预测步长对SVSRB 计算效率和计算耗时的影响，不同预测步长下搜索的SVSRB 见附录K图K1，对应的计算耗时和SNB 点数量见附录K 表K2。由图K1 和表K2 的计算结果可知：过大的预测步长将减少SVSRB 上SNB 点搜索数量，提高SVSRB搜索计算效率，但这将降低所搜索的SVSRB 精度；而过小的预测步长能够提高所搜索的SVSRB 精度，但会增加SVSRB 上SNB 点的搜索数量，降低搜索的计算效率。综合计算结果可得：在采用本文所提算法搜索含Hybrid-MTDC 的交直流系统SVSRB 过程中，为兼顾计算效率与计算精度，预测步长取为0.4。

4.1.5 三维SVSRB搜索

类似二维SVSR 构建方法，根据3.4 节所提三维SVSRB 构建方法，在三维有功注入空间内构建含Hybrid-MTDC 的交直流系统SVSR。图7 为以节点3 —5 有功注入为坐标轴搜索的含Hybrid-MTDC 的交直流系统SVSRB，图中ΔPλ3为标幺值。

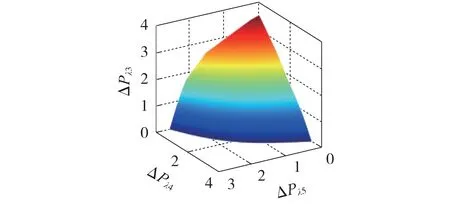
图7 含Hybrid-MTDC的IEEE 5节点测试系统三维SVSRBFig.7 Three-dimensional SVSRB of IEEE 5-bus test system with Hybrid-MTDC

含Hybrid-MTDC 的IEEE 5 节点测试系统中，三维SVSRB 内61 个SNB 点在不同计算误差范围内的统计结果如下：计算误差为［0.000 5，0.002］，SNB 点为50 个；计算误差为（0.002，0.004］，SNB 点为7 个；计算误差为（0.004，0.005］，SNB 点为5 个。该结果表明本文所提方法可高精度搜索含Hybrid-MTDC 的交直流系统三维SVSR。

进一步对比本文所提出的SVSRB 预测-校正算法与计及控制策略转换的CPF算法在构建含Hybrid-MTDC 的交直流系统三维SVSRB 的计算耗时。CPF算法的计算耗时为741 s，本文所提算法耗时为77 s。计算结果表明：相对CPF算法，本文所提算法的计算效率约提高了9.62 倍；这说明本文所提算法在构建含Hybrid-MTDC 的交直流系统三维SVSR 时具有较高的计算效率。

4.2 含Hybrid-MTDC的IEEE 118节点测试系统

在附录K图K2所示含Hybrid-MTDC的IEEE 118节点测试系统中，进一步验证本文所提SVSRB预测-校正算法在较大规模交直流系统中应用的可行性。

含Hybrid-MTDC 的IEEE 118 节点测试系统中各换流站初始运行参数见附录K 表K3。选择节点35、36 作为影响系统电压稳定性的关键节点，以节点35、36 有功注入为坐标轴，采用本文所提算法搜索该测试系统SVSRB，结果如图8 所示，图中ΔPλ35、ΔPλ36均为标幺值。在SNB 点处LCC、VSC1、VSC2换流站的控制策略分别为⑧、⑥、⑥。

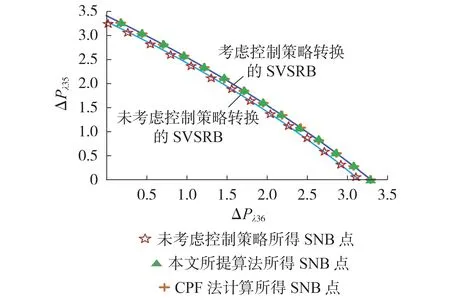
图8 含Hybrid-MTDC的IEEE 118节点测试系统二维SVSRBFig.8 Two-dimensional SVSRB of IEEE 118-bus test system with Hybrid-MTDC

进一步选择节点19、35、36 作为影响电压稳定的关键节点，以节点19、35、36 有功注入为坐标轴，采用所提方法搜索三维SVSRB，结果如图9 所示，图中ΔPλ19为标幺值。

图9 含Hybrid-MTDC的IEEE 118节点测试系统三维SVSRFig.9 Three-dimensional SVSR of IEEE 118-bus test system with Hybrid-MTDC

含Hybrid-MTDC 的IEEE 118 节点测试系统中，三维SVSRB 内61 个SNB 点在不同计算误差范围内的结果如下：计算误差为［0.000 5，0.002］，SNB 点为43 个；计算误差为（0.002，0.004］，SNB 点为18 个；计算误差为（0.004，0.005］，SNB 点为5 个。该结果进一步验证了所提算法在构建含Hybrid-MTDC 的较大规模交直流系统三维SVSRB 过程中具有较高的计算精度。

进一步对比本文所提出的SVSRB 预测-校正算法与计及控制策略转换的CPF算法在构建含Hybrid-MTDC 的IEEE 118 节点测试系统的三维SVSRB 的计算耗时。CPF 算法计算耗时为2 230 s，本文所提算法的计算耗时为308 s。计算结果表明：相对CPF算法，本文所提算法计算效率约提升了7.24 倍；在保证计算精度的基础上实现了较大规模含Hybrid-MTDC的交直流系统三维SVSRB高效搜索。

上述分析结果表明，本文所提算法可适用于不同规模含Hybrid-MTDC 的交直流系统二维和三维SVSR快速准确构建；算例结果验证了本文所提算法的可行性和通用性。