大规模风电经LCC-HVDC送出的送端电网频率协同控制策略

2023-09-11陈厚合于浩田刘先超李国庆

电力自动化设备 2023年9期

陈厚合，于浩田，刘先超，姜涛，李国庆

（东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林吉林 132012）

0 引言

随着“双碳”战略目标的提出，构建以新能源为主体的新型电力系统已成为我国能源战略的主要发展方向之一［1］。风能因其可再生性、无污染性和较好经济性成为最具发展前景的新能源之一［2］。我国风电资源主要集中在西北、华北、东北、西南等地区，而负荷中心主要集中在中东部地区。因此，大规模风电场经多回电网换相型高压直流（line commutated converter based high voltage direct current，LCCHVDC）线路输送到各负荷中心已成为当前我国风电大规模开发利用的主要形式［3-4］。

据国家能源局预测，预计到2060 年我国新能源装机占比将超过70 %，发电量超过50 %，成为电力供应主体［5］。随着风电渗透率持续增长，送端电网低惯量、弱调频能力的难题将进一步凸显，一旦发生直流闭锁故障，送端电网高频问题十分严重［6-7］。高频切机是解决送端电网高频问题的有效措施，但代价高昂，且切机准确度难以掌握，一旦发生过切事件，可能导致低频失稳情况，带来更大的经济损失［8-9］。因此，亟待研究高渗透率风电经LCC-HVDC送出的送端电网频率稳定控制策略。

目前，在提高大规模风电经多回LCC-HVDC 送出的送端电网频率稳定性方法中，直流频率限制器（frequency limit controller，FLC）发挥着重要的作用，其充分利用直流线路间功率分配的能力实现了准确、快速的功率调节控制，可有效解决由直流闭锁故障引起的高频问题［10-11］。文献［12］提出利用直流潮流法对直流FLC 备用容量、死区等参数设定值进行优化，以提升对频率峰值的抑制。在此基础上，文献［13］构建了一种直流FLC 参数的双层优化模型，通过分层求解获取直流FLC的最优控制参数。文献［14］基于改进的系统频率响应模型，提出了一种带死区的直流FLC 控制策略，在避免FLC 频繁动作的同时又保障了系统的频率稳定性。上述文献对高压直流线路附加的直流FLC 进行了研究，利用多直流线路之间的功率转移获得了一次调频能力，但高比例新能源送端电网的弱调频能力特性导致频率变化更加迅速，直流FLC 的功率转移极限受制于非故障直流的过载能力，迫切需要大规模风电参与一次调频过程，以避免新能源发电高频脱网。

风电机组参与一次调频常见的控制方法有超速减载、变桨距角以及二者相结合的综合控制方法［15-17］。文献［18］提出了一种风电机组参与系统调频的改进附加频率控制策略，根据频率变化修正控制参数，增强了系统的调频效果。文献［19］提出了一种计及动态频率约束的火电-风电机组联合调频策略，在满足经济性的同时提高了系统的稳定性。但上述频率控制方法均未能考虑高频问题严重的送端电网调频特性，未提出充分适用于送端电网的频率控制策略。

在送端电网的协调频率控制方面，文献［20］考虑含大规模风电送端电网的频率越限问题，基于模型预测提出了一种多源协同的调频策略，可改善送端电网频率动态响应特性。文献［21］提出了一种高比例水电系统的网省联合实时优化调度方法，利用日前预测协调技术，在提升送端电网新能源消纳能力的基础上，又进一步增强了送端电网的调频能力。以上研究通过多种调频措施来增强送端电网的调频能力，但未能充分考虑风电机组与直流线路协同配合的控制特性。

为此，面向未来高渗透率风电经LCC-HVDC 送出的送端电网的调频需求，本文提出一种风电机组与直流FLC 参与系统一次调频的协同控制策略，通过合理分配两者的调频时序和功率调制量，提升送端电网的频率稳定性。首先，分析风电与直流FLC的调频原理，建立包括风电与直流FLC 参与一次调频的送端电网频率响应综合模型，对比分析各调频控制参数的作用效果，根据电网一次调频要求整定风电与直流FLC控制参数；然后，结合两者的调频速度与调频能力差异，设计风电-直流FLC协同调频控制策略，在提高送端电网频率稳定性的同时，降低LCC-HVDC 线路过载和高频切机的风险；最后，通过修改的4机11节点系统和我国某实际送端电网进行仿真分析，验证了所提策略的有效性与可行性。

1 风电经多回LCC-HVDC 送出的送端电网结构及直流FLC控制原理和特性

1.1 含大规模风电的送端电网结构

以图1 所示的我国某实际送、受端电网的拓扑结构为例，大规模风电经多回LCC-HVDC送出，送端电网电源主要由同步电源和风电集群构成，经4 条LCC-HVDC线路分别送出至不同的受端电网。

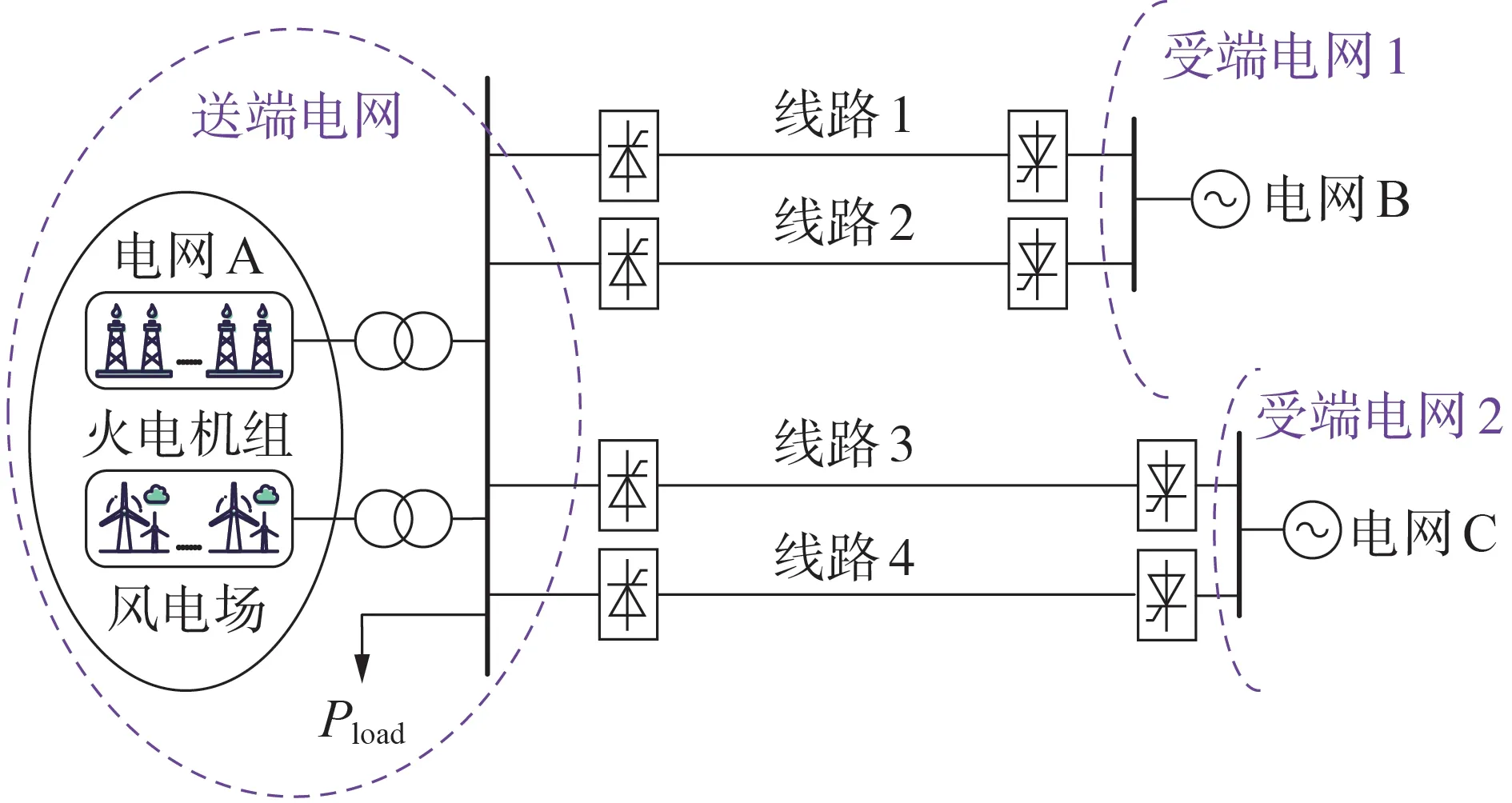
图1 我国某实际送、受端电网的拓扑结构Fig.1 Topology structure of some actual sending- and receiving-end power gird in China

结合我国某实际送端电网运行情况［12-13］，设送端电网总输出功率为5 000 MW，送端电网本地负荷Pload为2 000 MW，4 条LCC-HVDC 线路电压等级为±500 kV，其中LCC-HVDC 线路1、2 各输送功率500 MW，LCC-HVDC线路3、4各输送功率1 000 MW，总输送功率为3 000 MW，占比为60 %。送端电网呈现出“小网大外送”特点，多回直流线路对送端电网频率稳定性的影响尤为显著。

1.2 直流FLC控制原理

直流FLC控制原理与同步机组一次调频原理类似，当送端电网频率偏差超过直流FLC 的启动死区时，直流FLC通过比例积分（proportional integral，PI）控制得到非故障换流站附加功率转带指令，减小发生扰动后造成的送端电网功率不平衡量，抑制送端电网频率变化。常用的反向频差复归式直流FLC控制逻辑如附录A图A1所示。

1）当频率偏差未超过直流FLC 死区时，在限幅作用下，功率调制量总和ΔPsum为0。

2）当频率偏差超过直流FLC 死区时，以高频为例，附加功率调制量ΔPup的计算公式为：

式中：fH为直流FLC 控制的死区边界值；Δf为送端电网的频率偏差；KP和KI分别为比例和积分环节的系数。

由式（1）可知：直流FLC 在PI 控制作用下增大附加功率调制值，若频率偏差较大则会达到直流线路的过负荷运行极限状态，工程中附加功率调制值一般取1.2倍额定功率值；长时间处于超载负荷状态对LCC-HVDC 线路稳定运行造成很大威胁，当频率偏差再次回到死区之内时，积分环节反向调节直至输出的附加功率调制值为0。

1.3 直流FLC的控制响应特性

在未来大规模风电经多回LCC-HVDC送出的送端电网中，若直流线路发生闭锁故障，则风电的弱调频能力和最大功率点跟踪（maximum power point tracking，MPPT）控制特性可能造成更严重的高频问题，保障送端电网频率稳定面临着更加严峻的挑战。设置一回直流单极闭锁，功率波动约为10 %，分析不同风电渗透率（30 %、60 %）下有、无直流FLC 一次调频控制响应特性，仿真结果如图2所示。

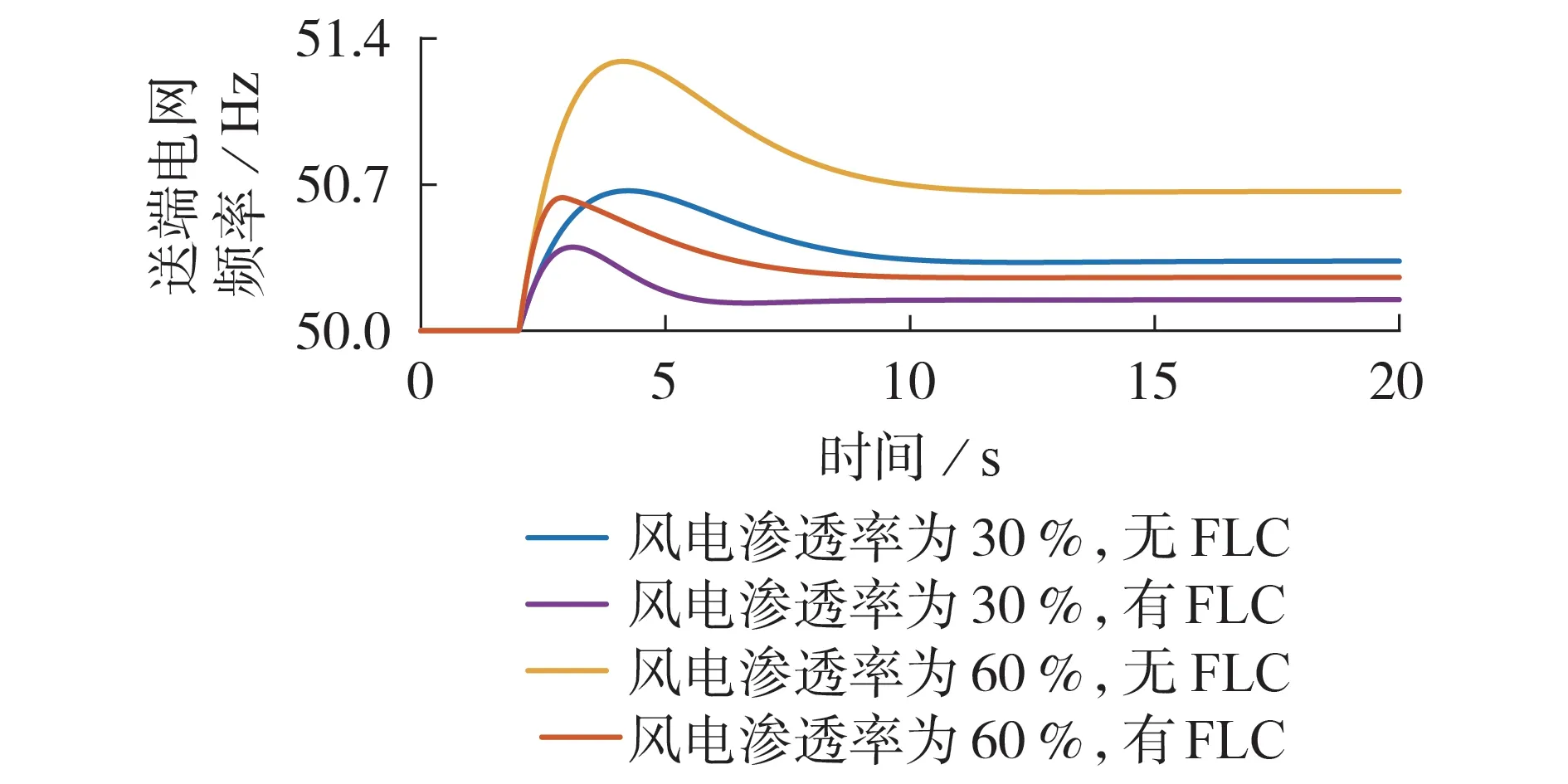
图2 不同场景下送端电网的频率响应曲线Fig.2 Frequency response curves of sending-end power gird in different scenarios

由图2 可知，直流FLC 可以有效抑制送端电网的高频问题，但随着风电渗透率增加，送端电网仅靠传统机组和直流线路进行一次调频已不能满足系统安全运行时对频率约束的要求。因此，在含高渗透率风电的多回LCC-HVDC 送端电网中，风电机组参与送端电网调频是必要的。

2 风电与直流FLC参与一次调频的送端电网频率响应综合模型

2.1 风电机组一次调频原理

通常状态下，风电机组运行在MPPT 控制模式，不具有调频能力，其运行时功率-转速特性曲线如附录A图A2所示。

针对高频问题严重的送端电网，风电机组可采用超速减载控制和变桨距角控制方法，将风电机组输出功率从MPPT 功率点降低至指定值点，从而参与系统的一次调频。该控制方法设计思路为：通过引入附加一次调频控制环节，将电网频率变化引起的附加功率指令输入转子侧换流器，进而改变风电机组的并网电磁功率；结合风电转子轴系的不平衡转矩使得转子转速或桨距角降低至减载运行点，完成风电机组主动参与送端电网的一次调频过程。风电机组一次调频控制原理如图3 所示。图中：PW为风电机组输出有功功率；Pref为风电机组输出有功功率调制量；PMPPT为风电机组最大功率点输出功率；ΔPA为功率指令值；ωr、ωref分别为风电机组转子转速及其参考值；Δωr为风电机组转子转速调制值；β、βref分别为风电机组桨距角及其参考值；Tservo为桨距角控制环节时间常数。

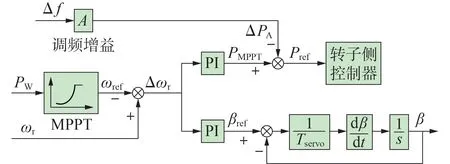
图3 风电机组下垂控制原理Fig.3 Droop control principle of wind turbine

首先，将频率偏差输入控制环节中，通过判断功率指令值ΔPA和风速值大小来决策转速及桨距角的调节顺序。在中、低风速下，先将功率调制信号输入转子侧控制器，进行转速调节，完成超速减载控制过程，当转速达到极限值，即1.2倍额定转速时，再通过PI 环节调整桨距角控制量，从而完成变桨距角控制过程；在高风速下，转速已达到极限值状态，则直接进行变桨距角控制，完成风电机组一次调频过程。

在《并网电源一次调频技术规定及试验导则》中规定风电场站一次调频调差系数应为2 %～10 %［22］，由此，本文选取3 个风电机组调频增益系数的边界值作为典型值，分别为10、30和50。

2.2 频率响应综合模型

对于含高渗透率风电的送端电网，在频率响应模型中加入可表征渗透率的变量［23］。本文所研究的送端电网发电侧由同步机组和风电机组构成，因此，定义同步机组的发电系数为K，计算表达式如下：

式中：PSG为同步机组发电量；Psend为送端电网总发电量。由式（2）可知：风电渗透率可表示为1-K（0≤K≤1）。

送端电网通常关注直流送端换流母线处的频率特性，将其等效为系统中心频率。综合考虑传统同步机组、风电机组一次调频及直流FLC，建立如图4所示的送端电网频率响应综合模型。图中：H为送端电网所有同步机组的总惯量系数；D为送端电网的阻尼系数；R为调速器的调差系数；FHP为汽轮机高压缸输出功率占比系数；TRH为再热环节时间常数；ΔPd为送端电网的电磁功率变化量；ΔPm为送端电网的机械功率变化量；K0为比例系数；ΔPup，max、ΔPdown，min分别为限幅器的上限值、下限值。

图4 含风电机组和FLC参与调频的系统频率响应模型Fig.4 Frequency response model of system with wind turbine and FLC participating in frequency regulation

为了便于计算，根据文献［24］，将同步机组的频率响应简化为图4 中的等值闭环控制模型，风电机组下垂控制特性用调频增益系数来表示，直流FLC控制特性用比例系数来表示。

由图2 可知，高渗透风电场景下直流闭锁引起的高频问题均会触发FLC，故忽略积分环节和死区，将直流FLC 看作比例控制过程，可得送端电网频率响应综合模型的闭环控制传递函数G(s)为：

式中：ωn为固有振动频率；ζ为阻尼比。

根据定义，D、R、A、H、TRH、FHP、K0、KP均为正数，且0≤K≤1，即1-K≥0。根据劳斯稳定判据，此时系统满足闭环系统稳定条件，因此，该闭环系统稳定。对应的特征方程和其特征方程系数应满足条件的具体表达式分别见附录A式（A1）、（A2）。

由闭环传递函数可得频率偏差的频域表达式Δf(s)，再通过Laplace反变换，可得系统频率偏差时域表达式Δf(t)，将其对时间t求导，可得频率峰值所对应时间tapex，如式（5）所示。进而可得频率最大值fapex，如式（6）所示。

式中：f0为基准频率。

频率最大值是衡量系统频率安全稳定的关键评价指标，对其影响因素进行研究具有重要意义。由式（6）、（7）可知，频率最大值fapex与风电渗透率1-K、风电机组调频增益系数A、直流FLC 控制的比例系数K0以及发生故障产生的功率波动量ΔP直接相关，因此，有必要对上述影响因子进一步研究。

2.3 频率响应模型的控制特性分析

为了进一步分析风电机组调频增益系数和直流FLC 比例系数对频率最大值的影响，根据不同功率波动量和风电渗透率分别设定场景1（ΔP=10 %，1-K=30 %）、场景2（ΔP=15 %，1-K=30 %）、场景3（ΔP=10 %，1-K=60 %）。由频率响应综合模型构建出不同场景下风电机组调频增益系数、直流FLC比例系数与频率最大值的关系曲线图，如附录A 图A3所示。

根据响应特性可知：直流FLC 比例系数和风电机组调频增益系数对系统频率升高具有较强的抑制作用，控制效果呈非线性；且二者交互影响，随着风电渗透率增大，调频增益系数的作用效果也更加显著，当调频增益系数取值较大时，直流FLC比例系数的影响将变得很小。因此，若能设置合理的参数取值，则可使风电机组与直流FLC 协调频率控制达到最佳效果。

3 送端电网频率协同控制策略

根据我国电能质量的要求：一次调频作用后稳态频率偏差的允许值为±0.2 Hz；为避免触发高频切机动作，需将频率控制在50.5 Hz 以下。因此，本文以fapex≤50.5 Hz 与fstea≤50.2 Hz（fstea为准稳态频率）作为频率约束条件。

对含多回LCC-HVDC 外送线路的送端电网，直流FLC利用直流线路之间的功率转移可以有效解决系统高频问题，但可能使得非故障直流线路濒临热稳定极限，且对受端电网造成一定的功率扰动。因此，设计满足送端电网频率安全约束下的直流FLC比例系数最小取值具有重要意义。

3.1 直流FLC比例系数最小取值设计

由式（6）可知，当时间tapex趋近于无穷大时，准稳态频率fstea的表达式为：

选取LCC-HVDC 线路1、3 发生连续单极闭锁故障为极限严重故障，造成的功率波动ΔP=15 %，并考虑风电渗透率为30 %、60 % 这2 种场景。在此基础上，由式（6）、（8）所示的频率约束条件可得在2 种场景下直流FLC 比例系数最小取值的计算表达式分别为：

由上述公式可知，在高风电渗透率场景下，一次函数斜率增大，调频增益系数的作用效果更显著。

本文送端电网模型中多回LCC-HVDC线路输送功率占比为60 %，当功率波动为15 % 时，直流FLC比例系数最大值为0.45。因此，当K0＞0.45 时，直流FLC 与风电机组一次调频协同控制作用效果不能满足频率约束条件，此时频率变化将会触发高频切机动作。

3.2 频率协同控制策略

综上，本文利用直流FLC 和风电机组下垂控制相配合的送端电网频率协同控制流程如附录A 图A4所示，其详细步骤如下。

1）根据已知系统确定送端电网频率响应综合模型中的参数（K、H、D、R、TRH、FHP和A）取值，并根据式（9）、（10）所示的K0-A对应关系确定直流FLC比例系数取值，获取初始运行条件。

2）检测送端电网频率，若f≥50.05 Hz，则同步机组、风电机组进行系统一次调频；若f≥50.15 Hz，则直流FLC 开始参与系统一次调频，实施协同控制策略。

3）当f≥50.5 Hz时，送端电网采用频率协同控制策略不能满足系统频率约束要求，将触发高频切机，流程结束。

4 仿真分析

为了验证所提送端电网频率协同控制策略的有效性，下面以修改后的4 机11 节点系统和图1 所示我国某实际送端电网为例进行仿真分析。仿真模型中同步机组的涡轮机、调速器和发电机均采用典型参数：H=4.5 s，D=1，R=0.033，FHP=0.3，TRH=6 s。直流FLC 的死区值设为±0.15 Hz，PI 环节中KP=0.222，KI=0.3。

4.1 修改后的4机11节点系统仿真分析

本节将4 机11 节点系统中节点7、8 间2 条支路替换为500 kV 的LCC-HVDC 输电线路，节点1 同步机组出力为980 MW，节点2 所连接的同步机组由84 台单机容量为5 MW的风电场代替，调整后的4机11节点系统的拓扑结构如附录B图B1所示。

根据4 机11 节点系统潮流分布特点，设定节点7 流向节点8 的LCC-HVDC 单条线路输送功率为400 MW，区域1 为30 % 风电渗透率的送端电网，风电机组调频增益系数取30，并根据式（9）求得所对应直流FLC 比例系数取值为0.271。设置单极闭锁故障，可得送端电网频率f、风电机组输出有功功率PW和LCC-HVDC传输有功功率PL的仿真结果见图5。

图5 不同控制策略的仿真结果Fig.5 Simulative results of different control strategies

由送端电网频率仿真结果可知：当直流FLC 参与调频时，fapex=50.596 Hz，未能满足所提频率约束条件；然而，在频率协同控制策略下fapex=50.435 Hz、fstea=50.199 Hz，均满足送端电网安全稳定运行的频率约束要求，这说明所提频率协同控制策略有效。由风电机组输出有功功率仿真结果可知：采用所提频率协同控制策略后，送端电网频率越限后风电机组下垂控制的响应速度很快，风电场输出功率由420 MW 迅速降低到325 MW；随着频率趋于稳定，输出功率又逐渐恢复至380 MW。风电机组输出功率约短暂下调22.6 %，这说明本文所提频率协同控制策略对抑制送端电网频率峰值发挥出非常显著的作用。由LCC-HVDC 传输有功功率仿真结果可知：当直流FLC 参与调频时，非故障LCC-HVDC 传输功率值瞬间达到最大值480 MW，即实际工程中所要求的1.2倍额定功率过载极限值，并持续20 s左右后开始逐渐降低，造成非故障直流线路极大的过负荷压力；而本文所提的频率协同控制策略中直流FLC 比例系数较小，使得传输有功功率最大值为458 MW，过载程度为0.144 p.u.，有效缓解了直流线路过负荷压力，也减少了对受端系统的功率扰动，可有效保障交直流系统安全稳定运行。

在风电渗透率为30 % 和60 % 这2 种场景下进行仿真分析，得到送端电网频率f、LCC-HVDC 传输有功功率PL、风电机组输出有功功率调制量Pref、风电机组转子转速ω和风电机组桨距角β的变化曲线，如附录B 图B2 所示，图中Pref和ω均为标幺值。由仿真结果可以看出，本文所提频率协同控制策略在高风电渗透率场景下的调频效果更好，即同规模同步机组和风电机组在相同调差系数下，风电机组的调频速度更快，且所需直流FLC比例系数更小，降低了系统功率波动，送端电网频率更稳定。由风电机组有功功率调制量、转子转速以及桨距角的变化曲线可看出：随着风电渗透率增大，即风电机组规模提升，风电机组参与一次调频的相对功率调制量反而减小。为进一步分析不同场景下所提控制策略的控制性能，将对比结果列于表1，表中线路过载程度和最大转子转速均为标幺值。

表1 不同风电渗透率下控制性能对比Table 1 Comparison of control performance under different penetrations of wind power

由表1可知，在风电渗透率为60 % 的场景下，风电机组的最大转子转速及最大桨距角均较小，相对功率调制量更低，LCC-HVDC 线路过载程度也明显减少，功率转移量随着风电渗透率增大而减小，频率最大值也更低。因此，在高风电渗透率送端电网中，本文所提策略具有更好的控制效果，在保证风电机组调频增益系数、直流FLC比例系数取得较小值时，又能够提升送端电网的一次调频能力，保障系统安全稳定运行。

4.2 某实际送端电网仿真分析

本节进一步以图1 所示我国某实际送端电网为例，验证所提频率协同控制策略在实际送端电网中应用的可行性。由于该实际送端电网的直流外送规模较大，直流FLC调制的功率范围较宽，有利于充分验证直流FLC控制参数整定的准确性，因此，本节分别从送端电网频率协同控制策略的有效性和参数整定的合理性两方面进行验证。

4.2.1 送端电网频率协同控制策略有效性验证

在风电渗透率为30 %且LCC-HVDC 线路1、3 发生连续单极闭锁（功率波动为15 %）的场景下，分别对比如下3 种控制策略：①控制策略1，仅直流FLC参与调频；②控制策略2，直流FLC 和风电机组在无协调方式下共同参与调频；③控制策略3，所提直流FLC 和风电机组协同控制参与调频。送端电网频率f、风电机组输出有功功率PW和LCC-HVDC 线路4 传输有功功率PL4仿真结果如图6所示。

图6 不同频率控制策略的仿真结果Fig.6 Simulative results with different frequency control strategies

由图6 可知：当采用控制策略1 时，受端电网频率最大值fapex=50.584 Hz，不能满足所提频率约束条件，且非故障LCC-HVDC 线路4 传输功率值瞬间达到最大值1 200 MW，在持续18 s后开始逐渐降低，造成线路极大的过负荷压力；而控制策略2、3 对频率峰值有着抑制明显作用，LCC-HVDC 线路过负荷运行程度得到明显改善。

相较于控制策略2，控制策略3对频率最大值抑制能力略低，二者相差0.024 Hz；而准稳态频率均为50.15 Hz；控制策略3对风电机组参与一次调频的功率调用量略高，相差16.3 MW，相当于控制策略3 多调用约1.09 % 风电场有功功率参与一次调频。但2 种控制策略在直流FLC 环节中产生的功率转移量却有很大的差别。

由LCC-HVDC 线路4 传输的有功功率变化曲线可知：正常状态下其传输的有功功率为1 000 MW；2 s 时LCC-HVDC 线路1、3 发生连续单极闭锁故障后，采用控制策略2时LCC-HVDC线路4传输有功功率最大值达到1 192 MW，接近直流过载能力最大值1.2 p.u.，而采用控制策略3 时LCC-HVDC 线路4 传输有功功率最大值为1 144 MW，线路过载程度为0.144 p.u.，与前者约相差4.8 % 的线路传输功率。这说明控制策略3 既有效缓解了直流线路过负荷压力，又减少了对受端系统的功率扰动，保障了交直流系统安全运行。

4.2.2 参数整定合理性验证

为了验证直流FLC比例系数取值与风电机组调频增益系数协同配合作用的有效性，首先根据《并网电源一次调频技术规定及试验导则》中所选用调频增益系数的典型值，并选取送端电网风电渗透率为30 % 的场景，由式（9）求得对应比例系数的取值，对应如下3 种场景：①场景1，当A=10 时，K300，min=0.394；②场景2，当A=30 时，K300，min=0.271；③场景3，当A=50时，K300，min=0.151。设定故障为2 s 时LCC-HVDC 线路1、3 发生连续单极闭锁故障，造成的功率波动ΔP为15 %，仿真结果如附录B图B3所示。

由送端电网频率仿真结果可以看出：3 种不同控制参数场景中，送端电网频率最大值与准稳态频率值均控制在约束范围内，即发生直流闭锁故障后，通过风电机组下垂控制和直流FLC的协同控制保障了送端电网频率稳定，验证了直流FLC 比例系数取值的有效性；随着调频增益系数的增大，即使直流FLC 比例系数减小，送端电网频率最大值也明显降低，这说明风电机组参与一次调频的功率变化量对抑制送端电网频率最大值具有较大影响。

由LCC-HVDC 线路4 传输有功功率的仿真结果可知：直流FLC 比例系数直接影响非故障直流线路的传输功率，在满足系统安全运行的频率约束条件下，可以通过增大风电机组调频增益系数减小直流FLC 比例系数，来有效降低LCC-HVDC 线路过负荷压力。

由风电机组输出有功功率调制量、转子转速和桨距角的变化曲线可知，风电机组通过超速控制和变桨控制协调配合，可有效参与送端电网一次调频：当增益系数较小时，仅进行超速减载控制；当增益系数较大时，在进行超速减载控制基础上，转子转速达到1.2倍的额定转速值后，启动桨距角控制。该下垂控制方法提高了风电机组的频率响应能力，有效改善高风电渗透率送端电网的频率稳定性。