浅谈运用数形结合思想培育几何直观的教学策略

陈华明

【摘 要】本文以笔者自身的教学实践为依据，浅谈在日常教学中如何运用数形结合的手段培育学生的几何直观素养。

【关键词】数形结合 几何直观 教学策略

在数学学习中，经常借助图形表征加深学生对数的感知能力。几何直观是应用图和表将知识或者问题形象化、具体化，并通过合理的思考、想象、猜想做出一些可行的结论，有助于把握问题的本质，有利于新知识的递增生成。因此，在小学阶段对学生几何直观素养的构建越来越受到数学一线教师的重视。

一、借形赋能，感悟几何直观

在教学中，我们将数学语言中的文字描述通过形象化的图形语言进行呈现，能够有效地揭示问题的内在本质，有助于梳理知识脉络，充分展现数学知识的特征，从而打破数学语言枯燥、难懂的思维定势，有利于学生进行观察、比较、分析等探究活动，变枯燥为生动、化抽象为具体。

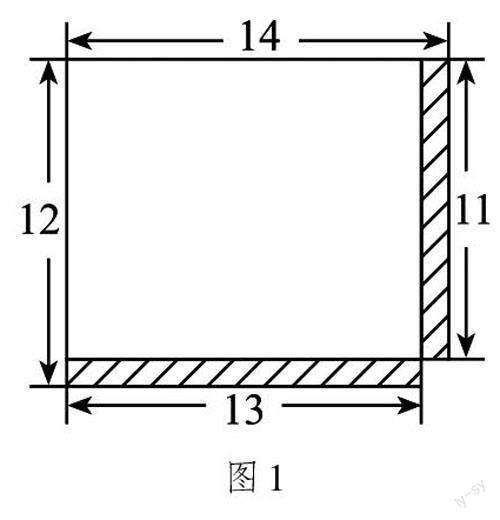
例如，在教学人教版三上“两位数乘两位数”时，笔者在课堂上出示练习题：比较13×12与14×11的大小。学生自然而然地想到通过计算能够实现两道算式的大小比较。如果我们为题目进行赋能，对算式进行转化，变为比较两个长方形面积的大小，借助几何图形将两个算式以另一种方式呈现在学生面前：一个长为13厘米、宽为12厘米的长方形和一个长为14厘米、宽为11厘米的长方形，运用多媒体手段将两个图形重叠在一起（如图1）。此时，笔者引导学生对图形进行观察，生1：“我发现把图形重叠后可以忽略掉相同的重合的部分13×11的面积大小，因此要比较13×12与14×11的大小，我们只要比较13×1与11×1的大小即可。”通过图形的具象化引导，把较为复杂、难算的算式用图形的语言进行呈现，不用计算，即可一目了然地比较出13×12＞14×11，而且能够一下子比较出它们相差多少。通过此过程，教师引导学生感悟借助图形解决问题的便捷性，从而进行几何直观素养的渗透。

二、化新为旧，孕育几何直观

形与数是数学中最重要的两个因素，如何将二者巧妙的连接和贯通，并为教学所用，就需要执教者合理利用。教师应该创造条件，引导学生改变认知方式，关联旧知、建立新知，要从学生已有的知识经验出发，借助形与数的关系，构建新的数学知识内容。

例如，在进行人教版五下“通分”的教学伊始，笔者设计了一个情境导入新课：“爸爸买了两块同样的蛋糕。爸爸吃了一块蛋糕的[5/6]，妈妈吃了另一块蛋糕的[2/3]，爸爸和妈妈谁吃得多？” 基于学生学习“分数的意义和性质”的相关内容，已充分掌握了运用画图表示分数的方法，在教师的引导下，大部分学生都能运用旧知中的方法解决新问题。一部分学生通过画图法成功解决了该问题：假设蛋糕是长方形的，把长方形平均分成6份，其中的5份涂上阴影，表示出爸爸吃了这块蛋糕的[5/6]，再画妈妈吃的[2/3]，通过观察发现，那么妈妈吃的[2/3]即为6份中的4份，而爸爸吃的[56]即为6份中的5份，由此得出“爸爸吃的蛋糕比妈妈多”这个结论。这时，笔者也通过课件展示妈妈所吃蛋糕大小示意图，引导学生观察、比较后发现[2/3]＝[4/6]的结论，因为[2/3]＝[46]，所以[2/3]＜[5/6]。也就是要比较两个异分母分数的大小时，首先要把异分母分数化为同分母分数才能比较出大小，从而引出通分的概念。在此过程中，运用直观的图形描述、分析数学问题，通过串联新旧知识之间的内在联系，促使学生领悟新知，初步孕育几何直观的模型。

三、化繁为简，构建几何直观

化繁为简或者化大为小是数学学习中常用的解题方法，当学生遇到一些复杂、抽象的问题时，往往因为错综复杂、混乱不堪的思绪而无从入手。此时，教师要引导学生想方设法从简单直观的知识入手，发现题目中蕴含的数学规律，再利用发现的规律去解决复杂问题。通过图形的表达，可以化繁为简、以退为进地解决问题，从而进行几何直观的素养构建。

例如，在教学人教版六下“整理与复习”中的“数学思考”时，笔者先抛出问题：一个小组10位同学进行两两握手游戏，一共握了几次手？先让学生尝试寻找答案，学生会利用画图连线的方法寻求解决方案，但由于数据比较大，关系错综复杂，相互之间穿插频繁，学生会有杂乱无章的感觉，产生畏难情绪。这时就需要教师引导学生进行有序思考，由浅入深、化繁为简。首先，从2个人握手开始考虑，将人抽象为2个点，连线画图后得出2个点只能连成1条线段，相当于握了1次手；接着，研究3个人握手，也就是在原来2个点的基础上又增加了一个点，通过连线画图后得出3个点可以连3条线段；再增加1个点，连线画图得出4个点可以连出6条线段；5个点可以连出10条线段。最后，把以上数据整理成表格，通过对表格中的数据推理可知：3个人两两握手1 + 2＝3（次），4个人1 + 2 + 3 ＝6（次），5个人1 + 2 + 3 + 4＝10（次）……以此类推，10个人1 + 2 + 3 + … +  9 ＝  45（次）。教師引导学生画图连线、整理表格，观察、感悟数据中蕴藏的规律，以此解决繁难的数学问题，进而构建几何直观数学素养。

四、借图析义，建立几何直观

小学阶段的数学问题经常借助画线段图来寻找解决问题的方法，帮助思维做出准确判断。它能准确、清楚地表示题中蕴藏的数量关系，简洁、形象地体现所要解决的问题，是一种重要的解决问题的辅助手段。面对比较复杂的数学问题，引导学生借助线段图分析问题，鼓励学生以形助学，尝试画图，借助图形分析数量关系，明确先求什么，再求什么。在列式解答后，让学生再结合算式和线段图整理解题思路，反思整个解题过程，感受画图策略的价值，经历借助图形思考问题的过程，形成初步的数学模型。

例如，在教学人教版五下“分数加减混合运算”时，教师出示题目：“一杯纯牛奶，乐乐喝了一半后，觉得凉，就兑满热水。他又喝了一半，就出去玩了。乐乐一共喝了几杯纯牛奶？几杯水？”教师的教学应该基于学生的经验基础：首先，学生的读题能力差，遇到文字较多、逻辑交叉的题目有排斥感；其次，学生的理解基于生活化的经验，在兑水的时候学生会想象成完全溶解在一起，无法分清哪些是水、哪些是奶，想象不出“水奶分离”的情况；最后，学生的思维架构不到题目主体，通常因无从入手而选择性放弃。教师的教学应基于学生的经验基础，这时，解题策略的生成就显得相当的重要。教师先让学生理解“混合成一杯的水和奶，实际上是由半杯水和半杯奶组成的”这一解题的关键思路，引导学生根据题意画出兑满水后喝的水和奶的线段图（如图2），寻找解题策略。通过画直观图等方法解决类似的生活化问题，在学生解答的同时，形成数学知识的模型，这样通过几何直观建构的数学模型就有高度。

编后记

《义务教育数学课程标准（2022年版）》提出了小学阶段核心素养的11个主要表现，对数学课程教学起到指导性的作用。小学数学教师应在教学中对学生适时渗透核心素养的培育，以提升学生的数学综合能力。本专辑的文章分别从量感和几何直观两个核心素养的主要表现出发，探讨核心素养的培养策略，希望能给一线教师带来启发。