新型半地下双层浅圆仓静态储粮的力学性能
2023-09-09金立兵张为博吴强王振清李闯焦鹏飞
金立兵,张为博,吴强,,王振清,李闯,焦鹏飞
(1.河南工业大学混凝土结构长期性能研究所,河南郑州 450001)(2.河南工大设计研究院,河南郑州 450001)
民为国基,谷为国命,粮食事关国运民生。粮食仓库的建设占用大量的土地资源,据统计,每1亿公斤粮食仓储设施占地达240亩以上,同时夏季高温会影响粮食品质。为了节约土地资源,应充分利用地下空间及浅层地能,积极寻求粮仓建设的新思路,提出了半地下双层浅圆仓。新仓型符合国家“碳达峰、碳中和”的政策,可有效支持粮食绿色仓储提升行动,确保粮食数量、质量和储存安全。
作为一种新仓型,国内外对于半地下双层浅圆仓的研究还甚少,但是浅圆仓在储粮方面有着较全面详细的研究。从19世纪Janssen公式提出以来,国内学者[1-4]对Janssen公式进行了修正;Janssen公式主要计算粮仓内粮食的侧压力和竖向应力,各国规范的一些设计规范和指南都是基于Janssen公式来编写的。John等[5]对不同国家的设计规范进行了分析探讨得出在不同的储粮条件下规范具有一定的缺陷型。在试验方面,Gandia等[6,7]使用玉米作为储料产品在填充、静态及卸料状态下进行试验得出了压力及摩擦力值并与预估值进行了比对验证了欧洲规范;Molenda等[8]从散体颗粒物理性质入手对粮仓内部散体-仓壁界面进行了研究,分析散粒体特性变化的原因并进一步得到仓壁产生荷载的规律。在数值模拟方面,国内外学者[9-11]提出了用于筒仓分析的有限元模型;Alauddin等[12-16]对基于有限元分析方法下的圆形筒仓受力进行了探讨,并对有限元模拟下的装粮条件进行了研究。研究团队前期对半地下双层浅圆仓施工阶段的力学性能进行了分析[17],提出了半地下双层浅圆仓的数值分析方法并进行了验证。
半地下双层浅圆仓正常使用阶段不同于施工阶段,正常使用阶段需要考虑仓内粮食荷载的作用。本文对正常使用阶段下不同储粮状况进行了数值分析,并对不同装粮高度下的半地下双层浅圆仓仓体受力与位移变化规律进行研究,为半地下双层浅圆仓的工程设计与推广应用提供技术参考。
1 半地下双层浅圆仓数值分析方法
研究团队前期通过采用实体单元对半地下双层浅圆仓进行建模并提出了数值分析方法(图1),对半地下双层浅圆仓的施工阶段进行了研究[17]。使用阶段与施工阶段的不同在于土体完全回填,半地下双层浅圆仓受到的永久荷载与施工阶段基本一致;外部可变荷载主要为风荷载、雪荷载与水土复合压力,仓体内储料荷载是仓储结构的特有可变荷载。
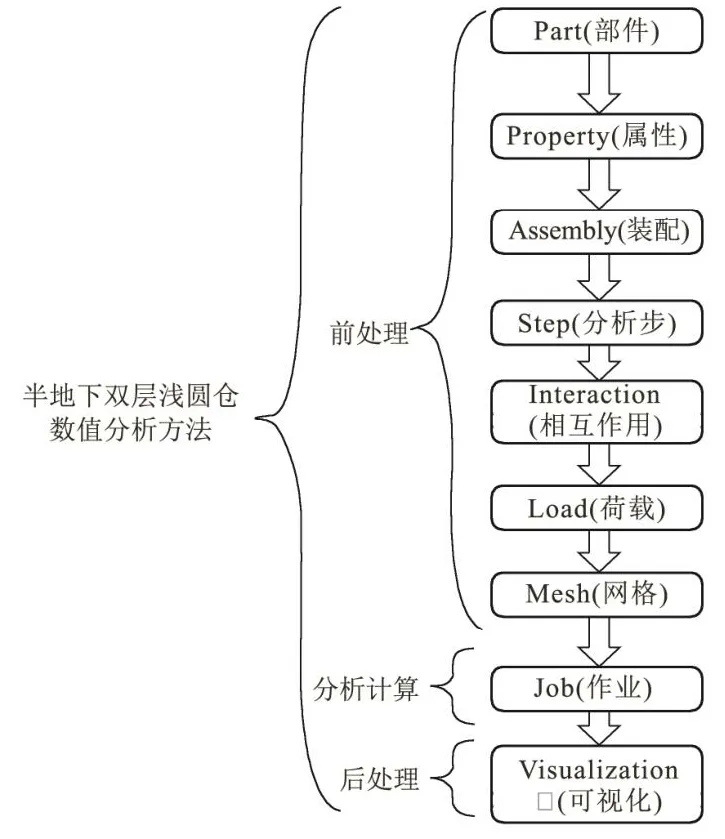
图1 半地下双层浅圆仓数值分析方法Fig.1 Numerical analysis method of semi-underground double-storey squat silo
1.1 半地下双层浅圆仓基本参数
半地下双层浅圆仓(图2)地下层仓壁高15.93 m,锥底高3 m,中心支撑筒高42.06 m,中心筒内径1.25m,地上层仓壁高18 m,仓壁内径25 m,厚0.5 m;仓壁与锥底交界处抗浮板外径27 m,厚1.2 m,中间层厚0.5 m,仓顶与水平面夹角为5 °,仓底与水平面夹角为15 °。

图2 有限元模型Fig.2 Finite element mode
1.2 储料荷载及边界条件
按《钢筋混凝土筒仓设计标准》(GB 50077-2017)有公式如下:
式中:
γ——储粮的重力密度,kN/m3;
s——储料顶面或储料锥体重心至计算截面处的距离,m;
k——侧压力系数,k=tan2(45°-φ/2);
φ——内摩擦角,°;
Pv——深度s处单位面积上的竖向压力,kPa;
Ph——深度作用于仓壁单位面积上的水平压力,kPa。
模拟选取小麦为储存粮食,根据上述规范取小麦物理参数:重力密度γ=8.0 kN/m3;内摩擦角φ=25 °;小麦对混凝土板的摩擦系数μ=0.40。由式(1)(2)可得到小麦的竖向压力和水平压力,考虑实际工艺需求要留出约2 m的作业空间,将计算的结果施加到半地下双层浅圆仓有限元模型上,其中储料对仓壁的水平压力是自上而下随深度逐渐增大的静态荷载,储料对仓壁的竖向摩擦是通过对仓壁赋予摩擦系数来实现。
由于半地下双层浅圆仓地下仓周围为土体,所以在水平方向能够达到自身相对平衡,但在竖直方向可能由于全仓重力影响造成土体的沉降而发生位移,也可能由于地下水的浮力影响产生竖直方向的变化,故对地下层仓底设置竖向约束,在抗浮板处设置位移转角约束,对地下层仓壁限制其转动。根据不同工况将储料荷载及其他荷载施加到半地下双层浅圆仓模型上,最后将模型进行网格划分(图3)后进行运算。

图3 网格划分Fig.3 Meshing
1.3 不同装粮方式分类
半地下双层浅圆仓有地下层、地上层共两层,装粮方式分四种工况见表1,针对四种不同工况进行数值分析。

表1 半地下双层浅圆仓正常使用阶段的四种工况Table 1 Four working conditions in the normal service stage of semi-underground double-storey squat silo
2 不同工况的应力与位移
2.1 应力分析
四种工况的地上、地下两层装粮均为满装粮,地上层满装粮装粮线设计为14 m,地下层满装粮装粮线设计为13 m。分别对四种装粮方式进行数值模拟,结果绘制四种工况下仓壁应力对比如图4。可以发现,地下层应力整体大于地上层,四种工况下地下层应力变化值较地上层大,这与地下层受到地下水土复合压力大且受力情况复杂有关。

图4 四种工况下模拟结果对比Fig.4 Comparison of simulation results under four working conditions
地上层仓壁在工况一与工况二,工况三与工况四的应力大小及走势近乎一致可见二层仓壁受力主要为粮食散体作用与下层影响甚微。深度为0 m处(中间层)工况三与工况四上侧约2 m内应力较工况一与工况二处大,产生这种的原因是地上层装粮产生对仓壁的侧压力导致的。工况三与工况四在中间层上方1 m内仓壁应力有一段减小的趋势是由于储料内部的剪切力、摩擦力等转移到中间层上,在靠近仓底与中间层接触处中间层“分担”了储料对仓壁的侧压力。工况三与工况四地上层在中间层附近处应力有极大值,表明对于在建设半地下双层浅圆仓地下层与地上层之间的连接对于结构安全性至关重要。
地下层仓壁在工况一条件下最大,在工况四条件下最小,工况二和工况四的受力分别较工况一和工况三小,地下层仓壁在深度-5 m~-12.5 m处应力在工况一较工况二条件下增大了约11%,工况三较工况四条件下增大了约9%,由此得出工况一为最不利工况,分析地下层不同装粮方式可知,地下层在装粮后储料对首层仓内壁的压力与水土复合压力对外壁的压力可以部分抵消,这使得地下层仓壁应力相应减小,基于力学分析指导实际储粮应优先在地下层储粮可以很好的减小仓壁应力。
2.2 不利工况下位移分析
由于半地下双层浅圆仓正常使用阶段的四种工况下地上层在工况四应力最大,地下层在工况一应力最大,但地上层整体最大应力远小于地下仓最大应力,考虑最大应力下可能对仓体整体产生不利影响,模拟得出此最不利工况下半地下双层浅圆仓的仓体位移云图。
图5为半地下双层浅圆仓在工况一下的位移云图,该图形的变形比例放大系数为1 000倍,选择这个比例是为了使变形更加清晰可见。最大位移变形在地下层仓壁自下而上1/3左右处,该位置附近同时也具有局部最大应力,造成这种现象的原因主要是由于地下水土复合力的作用;结构设计时应根据实际地质条件对仓体进行验算后对薄弱位置进行局部设计确保半地下双层浅圆仓结构的安全性。数值分析得到半地下双层浅圆仓在最不利工况下最大侧向位移为3.68 mm,即筒仓直径的0.014 7%,可见最不利工况下仓体的整体应力水平和侧向变形很小。

图5 最不利工况下位移云图Fig.5 Displacement under the most unfavorable condition
3 不同装粮高度的力学性能
3.1 不同装粮高度下仓壁应力规律
3.1.1 地下层仓壁应力分析
对半地下双层浅圆仓地下层在不同装粮高度下仓壁力学性能(此时地上层未装粮)进行分析,模拟装粮高度每增加1 m对仓壁应力产生的影响。将有限元模拟结果提取输出数据并整理,得到了半地下双层浅圆仓在不同装粮高度下地下层仓壁应力随深度变化如图6所示。

图6 不同装粮高度地下层仓壁应力Fig.6 Stress of underground storehouse wall at different grain loading heights
半地下双层浅圆仓地下层仓壁应力随着储粮高度的增加而减小。这是由于半地下双层浅圆仓地下层位于地下,受到水土复合压力数值较大且与粮食侧压力方向相反,储料对仓壁的压力可以部分抵消水土复合力对仓壁的影响。半地下双层浅圆仓在不同装粮高度下地下层应力从粮堆顶部逐渐增长,在距中间层约1/4处达到极值随后开始减小。
3.1.2 地上层仓壁应力分析
对半地下双层浅圆仓地上层在不同装粮高度下仓壁力学性能(此时地下层未装粮)进行分析,模拟装粮高度每增加1 m对仓壁应力产生的影响。将有限元模拟结果提取输出数据并整理,得到了半地下双层浅圆仓在不同装粮高度下地上层仓壁应力随深度变化如图7所示。

图7 不同装粮高度地上层仓壁应力Fig.7 Upper storehouse wall stress at different grain loading heights
地上层仓壁应力随着装粮高度的增加而增加,在距离二层仓底5 m左右处仓壁应力开始减小;且随着装粮高度的不断增加,减小到极小值的位置也在不断提高。仓壁应力随着装粮高度的增加而增大,但每个位置处增大的不尽相同,在地上层仓壁的2 m处附近增长表现的最为明显。在非常接近地上层仓底处(图中0 m处),可以看到剧烈增长的尖峰,这时由于仓壁局部弯曲现象和储料与仓壁共同作用导致的,在结构设计时可以对此重点考量。
3.2 不同装粮高度下仓底应力规律
3.2.1 中间层应力分析
将半地下双层浅圆仓地下层不装粮地上层装粮线从0 m逐次增长1 m至14 m时,将有限元模拟结果提取输出数据并整理,得到了半地下双层浅圆仓在不同装粮高度下中间层应力分布如图8所示。

图8 不同装粮高度下中间层应力Fig.8 Stress of the middle layer under different heights
整体应力增长趋势先有下降随后增长,再次下降后又增长。增长处主要在两端分别为靠近中心筒和仓壁与仓底接触处,为主要的承重位置;而整体趋势中两次应力减小造成这种现象的原因主要是由于装粮后储料内部应力与储料与仓体接触位置产生了拱效应,使得一部分竖向应力转移为水平应力。在距仓心3 m~10 m左右处随着装粮深度的增加,底部竖向应力先增大后逐渐减小,并在此过程中产生极大值,但在距仓心从11 m~12.5 m时(即装粮线接近半地下双层浅圆仓内径),应力又开始显著增长,约为极大值处的1.2倍,研究表明中间层应力变化受地上层储料高度影响大。
3.2.2 仓底应力分析
将半地下双层浅圆仓地上层不装粮地下层装粮线从0 m逐次增长1 m至13 m时,将有限元模拟结果提取输出数据并整理,得到了半地下双层浅圆仓在不同装粮高度下仓底应力分布如图9所示。
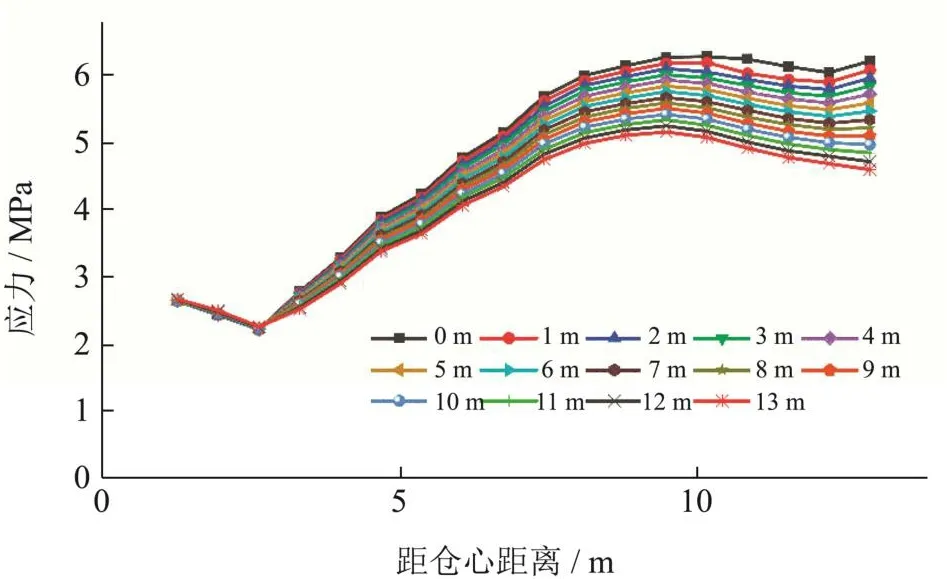
图9 不同装粮高度下仓底应力Fig.9 Stress at the bottom of the silo under different heights
从仓心起至往外侧至仓底边缘处的应力增长趋势先下降后增长再下降的趋势。不同装粮高度下在靠近中心筒处仓底应力变化不大为2.5 MPa左右是由于中心筒对复合力进行了分担;在距仓心2.5 m处开始增长至10 m(距外侧1/3处)处,仓底应力均匀增长至最大处;随后在10 m至仓底与仓壁接触处,应力区域稳定甚至有减小的趋势是由于半地下双层浅圆仓抗浮板减少了该位置附近处的复合力,研究表明仓底应力变化整体随地下层储料高度增长而减小是由于储料的荷载可以很好的与仓底的水土复合压力进行中和。
4 结论
本文对半地下双层浅圆仓静态储粮的受力性能进行了数值分析,探究了其在不同工况下以及不同装粮高度下仓体的力学性能,得到以下结论:
(1)对半地下双层浅圆仓在四种工况下进行数值模拟,得出全仓空仓为最不利工况。
(2)分别对半地下双层浅圆仓地下层和地上层不同装粮高度下仓壁应力分析可以得出,应力在地下层仓壁1/4左右处达到最大,在地上层仓壁与中间层接触处达到最大。
(3)中间层应力随装粮高度增加而增加并在中心筒附近和仓底外侧应力最大,地下层应力随装粮高度增加而减小。
本文可为半地下双层浅圆仓的结构分析提供理论指导与技术支持,为半地下双层浅圆仓的推广应用奠定基础。
