生物炭基肥离散元模型参数标定与试验

任德志，张露籍，宫元娟，孟 军，赫天一

（沈阳农业大学a.农学院/国家生物炭研究院/农业农村部生物炭与土壤改良重点实验室，b.工程学院，沈阳 110161）

生物质炭化还田是秸秆等农林废弃物资源化利用的可行途径，在土壤改良和作物栽培领域备受关注[1-2]。目前生产中生物炭主要用于加工生物炭基肥料，施用生物炭基肥料可在不增加额外作业流程的情况下，实现生物炭的还田，并发挥其改良土壤、促进作物生产的积极作用[3]。当前关于生物炭还田的研究多为探究炭土混合后对土壤及各类农作物生长的影响[4-5]，而对于以何种方式高效还田及如何提高生物炭还田的机械化程度鲜有研究。离散元法（Discrete Element Method）是一种用于预测散装固体行为的数值计算模拟技术，离散元模型已被广泛用于农业领域，它可以帮助缩短和改善农业机械及其部件的设计过程[6-9]。利用离散元法进行仿真试验，是反映生物炭炭基肥料还田过程的可行途径，而进行离散元仿真试验前，需对生物炭基肥料固体颗粒进行参数标定。

国内外已有相关生物质材料方面的参数标定理论与试验方面的研究，侯俊铭等[10]以蓖麻休止角为响应值，设计中心组合试验得到了蓖麻接触参数的最优组合；PACHÓN-MORALES 等[11]利用DEM 校准框架，以木制纤维素生物质的休止角、堆积密度和附着率为响应值，得到了生物质颗粒流动和与设备交互作用的离散元仿真模型；王韦韦等[12]利用EDEM 软件得到了玉米秸秆粉料致密成型离散元仿真模型最优化参数。然而值得注意的是，生物炭基肥料作为一种备受关注新兴农业投入品，尚未有离散元法参数标定和实验方面的研究。

本研究在前人研究的基础上，提出一种真实试验与仿真试验结合的方法测定炭基肥颗粒的物理特性，以物理试验为参照建立生物炭炭基肥颗粒离散元模型并标定仿真参数，旨在为实现生物炭科学高效还田、仿真生物炭基肥料还田过程和设计生物炭基肥料专用还田机械提供新的理论依据。

1 材料与方法

1.1 试验材料与物料特性

试验材料为沈阳农业大学国家生物炭研究院监制的生物炭基肥料，该颗粒材料平均含水率为5%，百粒质量5.26 g，球形度92%。从炭颗粒试验样品中随机抓取百粒，测定记录颗粒粒径，重复8 次，炭基肥颗粒堆俯视图和粒径分布如图1，2 mm粒径占比35%；3 mm颗粒占比42%；4 mm颗粒占比23%。

图1 生物炭基肥颗粒及粒径分布Figure 1 Biochar-based fertilizer particles

1.2 堆积角的测量

堆积角是表征颗粒物料流动、摩擦等特性的宏观参数，是仿真试验中的关键响应指标。参考球形颗粒肥料的参数标定研究[13-16]，选择运用圆筒提升法测量颗粒堆积角（图2）。

试验所用装置和材料包括:物理特性万能试验机、内径40 mm 套筒、游标卡尺和载物平板。试验过程为：圆筒置于平板中心位置，测量物理特性的886 粒炭基肥充满于圆筒内；试验机夹具固定圆筒后，以0.1 m·s-1的速度将圆筒提起，使生物炭形成颗粒堆，静止5 min，剔除滚出颗粒堆外的颗粒，利用游标卡尺测量颗粒堆底部最大直径d和颗粒堆最大高度h，生物炭炭基肥颗粒堆积角为：

试验重复5次，结果如表1，最后计算得到堆积角平均值为23.65°。

1.3 接触模型

离散元软件ESSS Rocky DEM 提供了专用于预测农业设备中颗粒行为所需的模型，仿真模型的选取直接影响仿真结果，模型包括重力模型、接触模型以及热模型。炭基肥颗粒之间的作用存在粘结现象，合理的选择接触模型可以得到与实际试验相近的结果。本研究设置接触参数如表2。

表2 接触参数模型设置Table 2 Contact parameter model setup

1.3.1 法向力模型 DEM模型中的法向力模型需要满足两个条件：该力是一个反作用力；法向力模型满足高能量耗散。本研究中法向力模型选择Hertzian Spring Dashpot 模型，该模型与Linear Spring-dashpot模型区别在于Hertzian模型中法向力的弹性和阻尼分量是重叠的非线性函数[17]，其计算公式为：

式中：Fn为法向力值；为刚度系数；为阻尼系数；sn为接触法线重迭量；为触法线重迭量时间导数。

根据TSUJI 等[18]研究，Hertzian Spring Dashpot 模型中刚度系数阻尼系数的定义与Linear Spring-dashpot 模型中的定义类似，法向阻尼系数的值可通过黏性能量耗散与非弹性碰撞的能量耗散相匹配来确定，而非弹性碰撞的能量耗散则由恢复系数的值来确定，则刚度系数和阻尼系数为：

式中:E*为降低后的杨氏模量；R*为有效或等效半径；η为阻尼比，其值与恢复系数有关；m*为接触的有效质量或等效质量。其中计算公式为：

式中：m1和m2分别为相互接触粒子的质量，而m是与边界接触的粒子的质量。

Hertzian Spring Dashpot 模型适用于球体颗粒，并且该模型适用于所有切向力模型，与3种附着力模型也有较好的适配性，综上考虑选择Hertzian Spring Dashpot 模型。

1.3.2 切向力模型 切向力模型用于计算接触力的切向分量，包括Linear Spring Coulomb Limit 模型、Coulomb Limit 模型和Mindlin-Deresiewicz 模型。本研究选择Linear Spring Coulomb Limit 模型，该模型中的切向力是弹性摩擦力，若切向力视为纯弹性，其与时间t的关系式为：

式中：为模型切向力为前一瞬间切向力的值；Δsτ为粒子的切向相对位移；Kτ为切向刚度。

式（6）中的切向刚度与粒子材料相关。在此模型中，切向力不能超过库伦极限，因此切向力的完整表达式为：

式中：为随时间变化的接触法向力；μ为摩擦系数，若在接触处无滑动选择静摩擦系数μs，存在滑动选择动摩擦系数μd。

在模拟计算炭基肥颗粒中引用Coulomb Limit 模型不适用于颗粒少精度高的仿真试验；选择Mindlin-Deresiewicz 模型则会禁用滚动阻力模型。综上考虑选择适用于所有模型的Linear Spring Coulomb Limit 模型。

1.3.3 附着力模型 上述模型中描述的正常接触模型适合于模拟非粘性和干燥的颗粒材料，实际上，绝大多数颗粒状材料都会含有不同的水分，所以会产生粒子与粒子、粒子与其他表明黏附的现象。为了捕捉这种行为，必须补充附着力模型，以准确预测其流动特性。需要注意的是，颗粒之间的粘附力是应力的一个函数，Rocky中的附着力模型通过将黏附力和接触力缩放来捕捉这一现象。

本研究中选择的附着力模型为JOHNSON等[19]提出的JKR模型，在JKR模型中，粒子间的接触面积比Hertzian理论中所所预测的略大，这是表面能加入到系统总能量中的结果。选择JKR模型后，法向力的附着力公式为：

式中：Fn,adh为法向附着力；Γ为模型参数，该系数的值与材料有关；E*为有效的杨氏模量；a为粒子与粒子或与表明之间的接触半径。

JKR 模型会影响法向和切向力模型，Hertzian Spring Dashpot 模型中的弹性部分需要修正，并以接触半径a的函数表达，即：

式中:R*为有效粒子半径。

JKR 模型拥有夯实的理论基础，被广泛应用于附着力模型中，由于表面能可以通过实验测量，该模型不需要校准并且可以用于模拟球形颗粒。在Rocky软件中JKR模型需要与Hertzian Spring-dashpot 模型一起使用。

1.3.4 滚动阻力模型 滚动阻力是在建模中引入与粒子滚动运动相反的力矩时使用的通用名称，通常将该力矩作为一种实用的方法来表示滚动球体上的非球形效应或其他类型粒子上的表面不规则性效应。本研究选择的滚动阻力模型为Type C:Linear Spring Rolling Limit[20]。

Linear Spring Rolling Limit 是一个弹塑性模型，该模型将黏性阻尼项替代为滚动刚度值以更好的模拟滚动阻力行为，其中滚动刚度为：

式中：Kr为滚动刚度；Kτ为切向刚度；Rr为滚动半径，定义为在给定时间内连接粒子中心点和接触点的向量，若滚动阻力为纯弹性力，则滚动阻力为：

Rocky软件中提供两种滚动阻力模型，另一模型Type A 只适用于光滑滚动，由于生物炭颗粒之间存在黏连作用，所以滚动阻力模型选择可配合附着力模型的Type C:Linear Spring Rolling Limit模型。

1.4 离散元仿真模型

Rocky软件材料本构提供了用于描述农业颗粒行为所需的数学模型，通过Rocky建立生物炭粒子。基于已完成的颗粒物理特性试验得到生物炭颗粒球形度为92%，根据离散元法理论[21]，当颗粒非球形度小于10%时，设置球体颗粒对仿真分析结果影响极小，所以建立Biochar粒子，形状类型设为球体颗粒，粒径分布参考物理特性试验设置为:4 mm 直径的粒子数目占总颗粒数25%、3 mm 直径的粒子数目占总颗粒数40%、2 mm 直径的粒子数目占总颗粒数35%。在SolidWorks 中建立圆筒和钢板的三维模型，导出为STL 格式并导入Rocky 软件中（图3）。

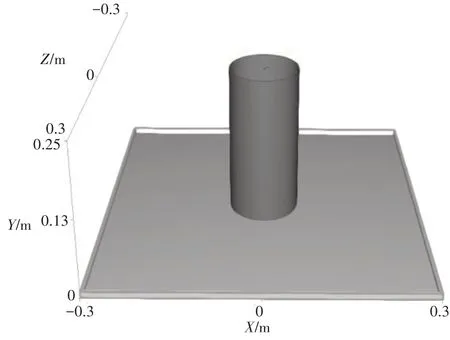
图3 仿真模型Figure 3 Simulation model

为更好地对照真实试验，参考设置圆筒上升速度为0.1 m·s-1，粒子生成数目886个，生成时间2 s，总仿真时长8 s。为记录设置不同的接触参数组合下所产生的炭颗粒堆积角，在每次仿真结束后创建在t=8 s 处粒子的交叉散点图，它可以观测到在某一瞬间粒子堆积在X-Y平面上的投影（图4），根据交叉散点图可确定本次接触参数组合所得到的堆积角，计算方法同式（1）。

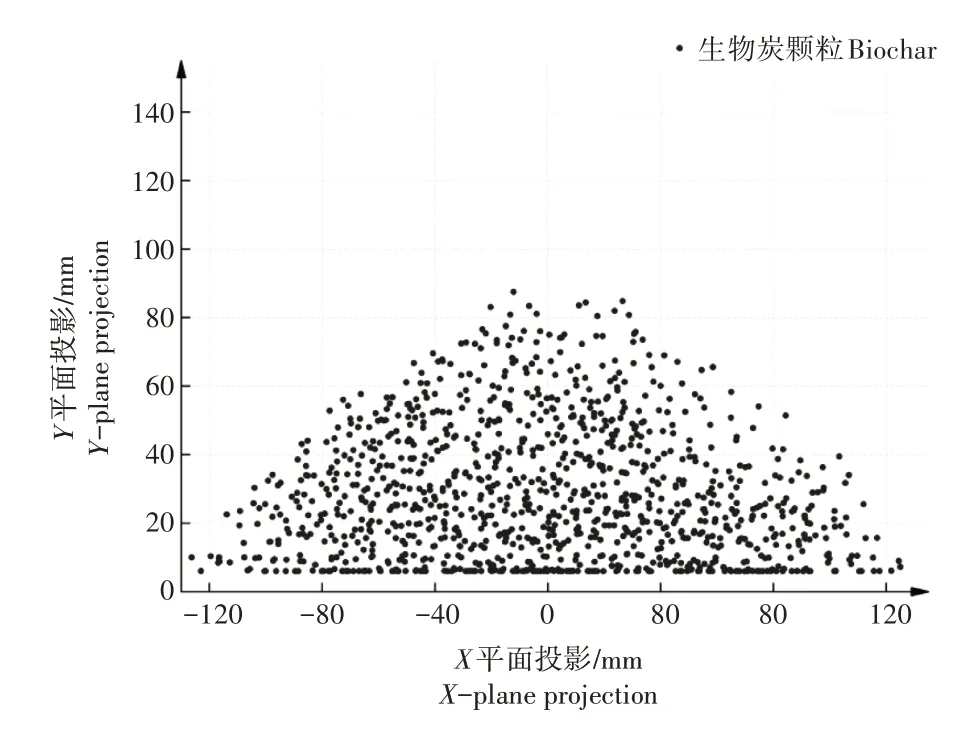
图4 交叉散点图Figure 4 Cross-scatter plot

2 试验设计与结果分析

2.1 Placket-Burman试验

由于物料的接触参数中并非所有参数都对堆积角有显著影响，所以，本研究设计Placket-Burman 试验，筛选出关键仿真接触参数，P-B 试验因素水平如表3。

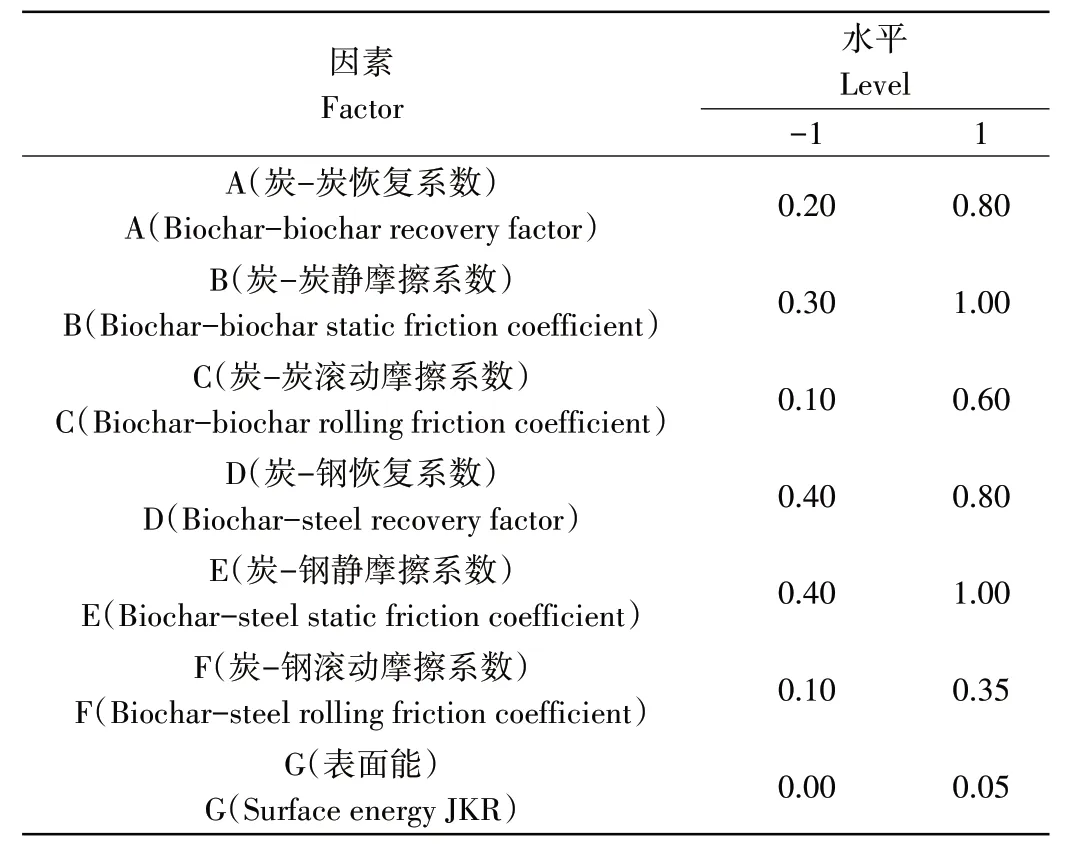
表3 接触参数模型设置Table 3 Contact parameter model setup

P-B 试验方案及结果如表4，其中H、J、K、L 为虚拟参数，即空白列。对试验结果进行方差分析如表5，结果表明炭-炭滚动摩擦系数（C）、炭-钢滚动摩擦系数（F）和炭颗粒表面能（G）对生物炭颗粒的堆积角影响显著。

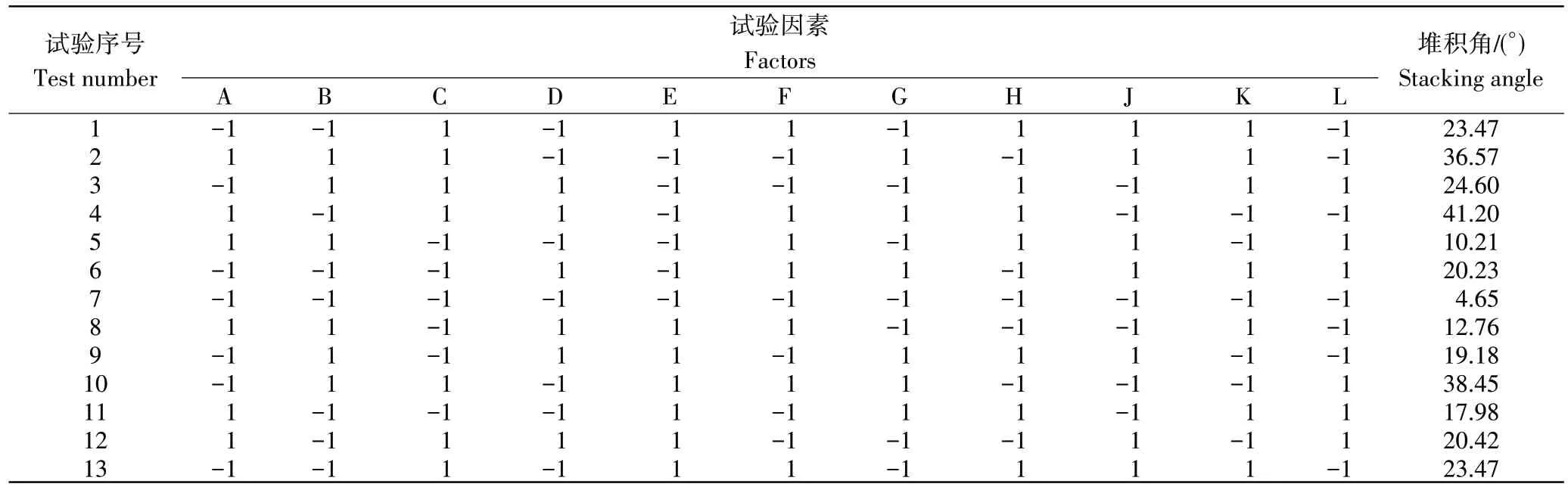
表4 Plackett-Burman试验方案及结果Table 4 Plackett-Burman test protocol and results

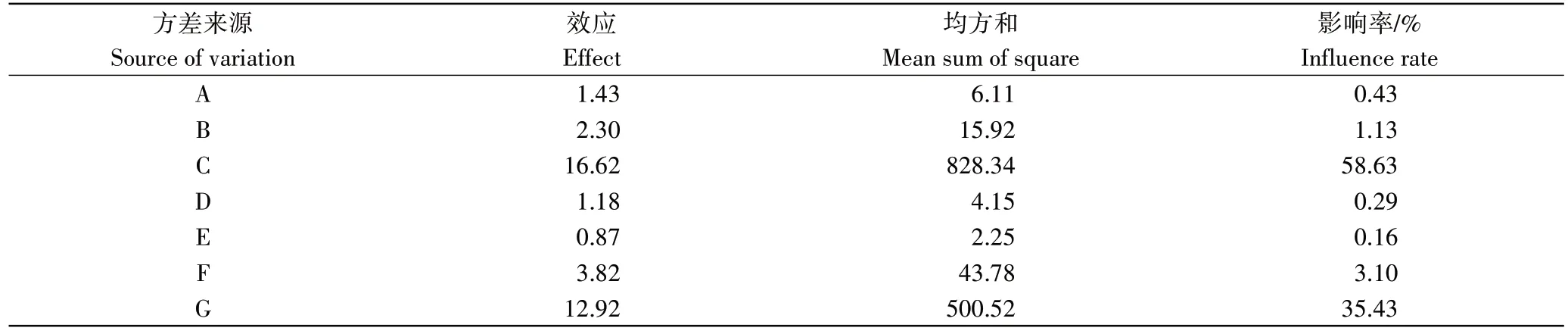
表5 Plackett-Burman试验方差分析Table 5 Variance analysis of Plackett-Burman test

2.2 最陡爬坡试验

对选择的显著影响参数进行最陡爬坡试验以确定显著性参数最优值区间，试验方案及结果如表6，结果表明:随着炭-炭滚动摩擦系数（C）、炭-钢滚动摩擦系数（F）和炭颗粒表面能（G）的值逐渐增大，仿真堆积角逐渐增大，相对误差先减小再增大，其中第3组试验的相对误差最小，则选择第3组显著性参数值为中心水平，建立回归模型求解参数组合最优值。

表6 最陡爬坡试验方案及结果Table 6 Steepest climb test protocol and results

2.3 Box-Behnken响应面试验

根据最陡爬坡试验结果，选择第3 组试验因素值为中心水平值，第2 组、第4 组试验因素值为-1 和1 水平值，设计Box-Behnken响应面试验，试验方案和结果如表7。

表7 Box-Behnken试验方案及结果Table 7 Box-Behnken test protocol and results

通过Design Expert试验分析软件对试验结果进行显著性检验，得到关于堆积角的方差分析如表8。通过检验结果可发现，模型R1的显著值p＜0.001，并且失拟项p＞0.05，说明本次多因素试验的回归方程检验达到高度显著，并且拟合度较好，因此可以对本次试验数据结果进行进一步的分析和优化。去除不显著项后得到的多项式回归方程为：

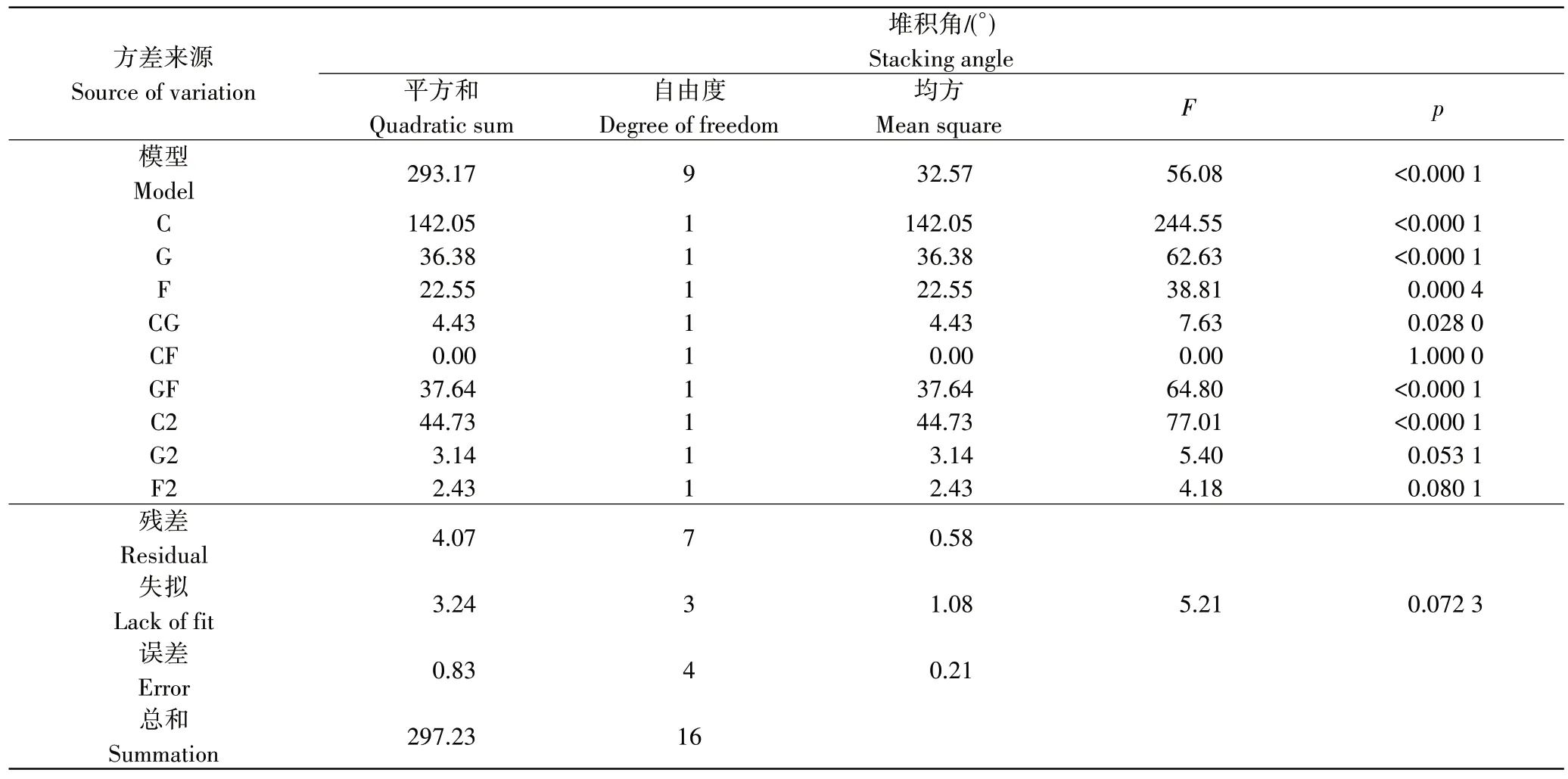
表8 Box-Behnken试验方差分析Table 8 Variance analysis of Box-Behnken test

式中:A为炭-炭滚动摩擦系数（C）编码值；B为炭颗粒表面能（G）编码值；C为炭-钢滚动摩擦系数（F）编码值。

将Design Expert 中得到的多项式回归方程导入绘图软件Origin 的矩阵方程中，通过3D 映射曲面图绘制出三因素对堆积角的响应面图如图5。通过方差分析和响应面图可知，炭-炭滚动摩擦系数（C）和炭颗粒表面能（G）单独对堆积角影响显著；炭颗粒表面能（G）和炭-钢滚动摩擦系数（F）的交互影响对堆积角影响显著，并且当炭颗粒表面能（G）增大时，堆积角越趋近于真实试验值23.65°。综上可知炭颗粒表面能（G）对堆积角的影响最为关键。

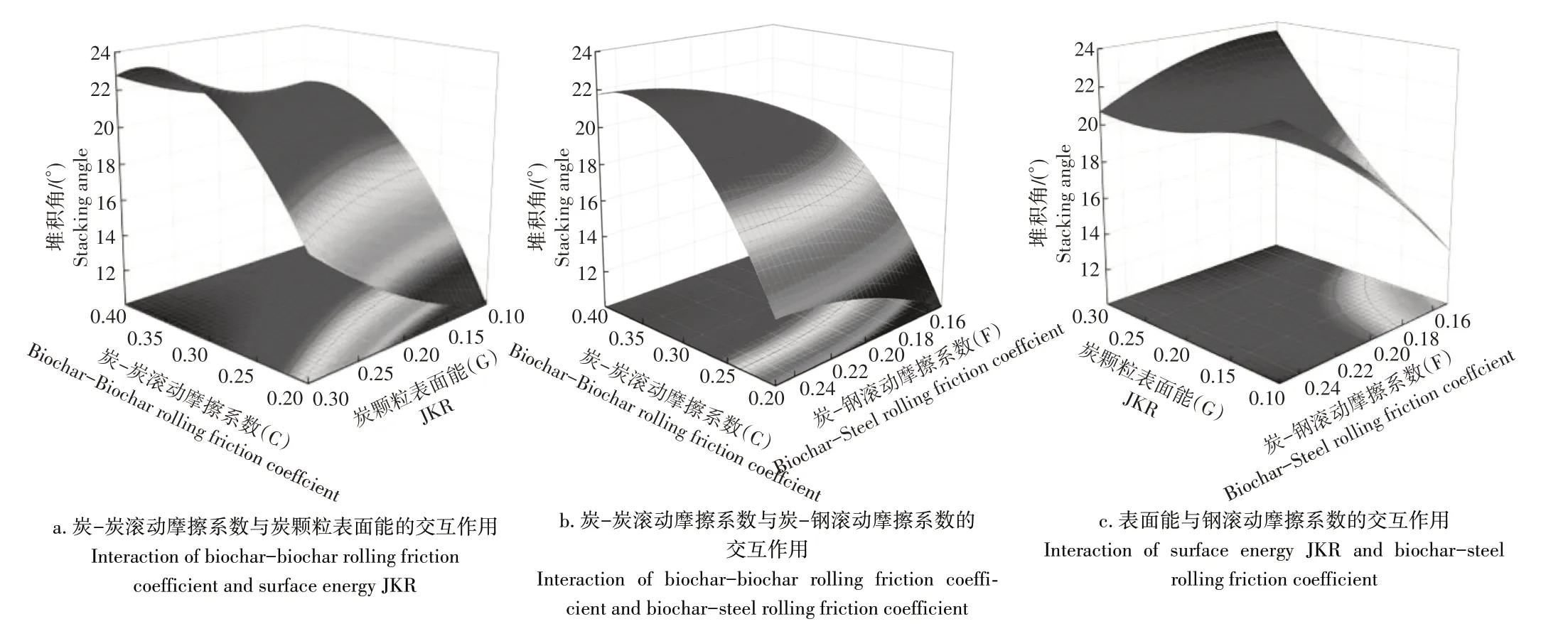
图5 多因素交互作用的响应面图Figure 5 Multi-factor response surface diagram

通过Design-Expert 软件中试验数据参数优化模块，设置边界条件为堆积角趋近于目标值23.65°，得到最优参数组合为:炭-炭滚动摩擦系数0.36，炭颗粒表面能0.30，炭-钢滚动摩擦系数0.20。

2.4 验证试验

为验证所得最优化接触参数值的准确性，以炭-炭滚动摩擦系数0.36、炭颗粒表面能0.30、炭-钢滚动摩擦系数0.20、其他接触参数取中间水平值（炭-炭恢复系数0.5、炭-炭静摩擦系数0.65、炭-钢恢复系数0.6、炭-钢静摩擦系数0.7，其余设置不变进行离散元仿真试验，测得堆积角为23.48°，与实际试验测定堆积角23.65°的相对误差为0.72%。仿真试验图与实际试验图对比如图6，两者无明显差异。

图6 试验对比图Figure 6 Test comparison figure

3 讨论与结论

国内关于生物炭的研究基本来源于由陈温福院士带领成立的生物炭工程技术研究中心，其研制的Ⅰ级生物炭适用于东北地区土壤，但该团队未对生物炭如何还田以及如何更好的还田做出详细的研究。关于离散元参数标定的研究已经趋于成熟，与其他研究相比，生物炭还田的仿真过程类似于肥料颗粒入土，但两者物理特性的差异使得需要对生物炭颗粒进行参数标定，以为后续的生物炭还田技术研究提供理论参考，其结果的准确性直接影响后续对于生物炭还田工作过程仿真的真实性。

本研究结果表明，基于实际物理实验堆积角测定值23.65°，标定生物炭颗粒接触参数。设定离散元接触模型，通过Placket-Burman 试验筛选得到对生物碳颗粒堆积角有显著影响的参数:炭-炭滚动摩擦系数、炭颗粒表面能和炭-钢滚动摩擦系数。根据最陡爬坡试验结果确定参数的最优质区间，设计Box-Behnken响应面试验建立堆积角与3个显著参数的回归模型。显著性检验和响应面分析表明:炭-炭滚动摩擦系数和炭颗粒表面能对堆积角均有显著影响，并且炭颗粒表面能和炭-钢滚动摩擦系数之间存在明显交互作用。根据最优化参数组合:炭-炭滚动摩擦系数0.36、炭颗粒表面能0.30、炭-钢滚动摩擦系数0.20，重新设置接触参数并进行验证试验。试验表明，在此接触参数组合下仿真得到的堆积角23.48°，与实际测定值相对误差为0.72%，所标定的生物炭颗粒离散元模型参数真实可靠。