基于蒙特卡洛法的粮食侧压力下SIW墙板可靠性及灵敏度分析
2023-09-07丁永刚宋战炯陈科委
丁永刚,宋战炯,陈科委*,刘 强
1.河南工业大学 土木工程学院, 河南 郑州 450001
2.河南省粮油仓储建筑与安全重点实验室, 河南 郑州 450001
粮食平房仓是一种应用广泛的储粮仓型,其墙体多是黏土砖砌筑建造而成,具有仓储量大、建造周期短、一次性投资少等优点,但存在容易产生通缝、气密性差、承载力不足等缺点。“结构-隔热”一体化复合墙板(SIW墙板)作为一种新型粮食平房仓墙体构件,由两层钢筋混凝土板、一层挤塑式聚苯乙烯(XPS)保温板,通过玻璃纤维增强塑料(GFRP)做连接件连接组合而成,能发挥钢筋混凝土构件抗弯受拉及保温隔热双重功能。粮仓墙体承载力研究通常在确定性条件下开展,但SIW墙板结构组成复杂,且工程中充满着随机性,如施工工艺不规范、制造流程不标准等造成SIW墙板结构参数出现偏差,影响其力学性能。荷载、结构、材料等因素均会对SIW墙板的失效产生影响,但影响程度未知。可靠度理论将随机性引入到结构分析中,用概率的结果表示结构的某一性能,直观地反映结构在随机性条件下的失效状态[1]。粮仓关系到国计民生,有必要将随机性因素考虑到SIW墙板结构分析中,研究不同失效准则下其可靠性能及参数的影响能力,可更好地设计SIW墙板结构。
SIW墙板本质上是提出了一种专门用于粮食平房仓的新型夹芯复合墙板,其设计理念、研究内容、分析方式大多由传统混凝土夹芯复合墙板引入。Huang等[2]通过有限元分析了混凝土夹芯板的结构性能,发现斜杆直径对结构力学性能影响显著。刘才华等[3]通过静力加载试验研究了夹芯墙板的平面外抗弯性能,发现外墙板底部点支撑的个数和间距对其平面外抗弯性能影响显著。孙蕾[4]通过试验研究了SIW墙板的力学性能,发现墙板在粮食侧压力作用下具有良好的抗弯刚度和承载能力,连接件能够使内外叶墙板协同变形,具有较好的整体性[5]。可靠性分析有一次二阶矩法、响应面法、蒙特卡洛法等[6],其中蒙特卡洛法能够规避隐式功能函数求解的难题,且计算结果最为精确[7]。陈桂香等[8]利用蒙特卡洛随机有限元法对地下筒仓开展了可靠性、灵敏度研究,探讨了随机因素对地下筒仓失效的影响。王彦杰[9]采用蒙特卡洛法对钢筒仓结构开展了可靠性分析,研究了物料密度等参数对Mises应力的影响。刘腾龙[10]采用蒙特卡洛随机有限元法对大直径钢筋混凝土料仓开展了可靠性研究,分析了料仓几何尺寸、材料及荷载的不确定性对料仓仓壁的影响,为结构优化设计、施工控制等提供依据。周佳乐等[11]采用蒙特卡洛法对UHPC梁抗扭承载力状态进行了可靠度分析,研究得到了各关键参数对可靠度的敏感性。崔晨星[12]采用响应面法对地下大直径粮食筒仓开展了灵敏度分析,得到了对其体系可靠度影响较大的参数。金燕等[13]考虑热弹流润滑、材料属性等参数的随机性,对航空轴承进行了疲劳可靠性分析,验证了智能方法良好的计算性能。蒙特卡洛随机有限元法将有限元分析与可靠性设计结合[14],对影响结构可靠性的材料尺寸、特性等随机参数进行统计分析[15]。通过随机参数抽样,计算结构失效概率,研究并量化影响结构失效概率的各随机输入参数的灵敏度及相关性,确定影响SIW墙板可靠度的关键参数[16]。
SIW墙板是新型构件,构成复杂,墙板的结构几何特征、各材料性能均具有不确定性,设计过程中并不能完全保证所有参数处于最优。鉴于此,作者采用蒙特卡洛随机有限元法,考虑SIW墙板在最大粮食侧压力作用下,分析粮食荷载、SIW墙板几何尺寸、材料特性等随机参数的不确定性对其可靠性的影响,计算不同失效准则下的失效概率,评估SIW墙板在随机性条件下的可靠性,量化随机参数对其可靠性的影响能力,为SIW墙板结构设计及优化提供参考依据。
1 有限元分析
1.1 SIW墙板构造
SIW墙板两层钢筋混凝土板分别为内叶墙和外叶墙,其中内叶墙与粮食散体直接接触,相比外叶墙较厚,主要承担粮食侧压力作用。内叶墙由两层钢筋网片和混凝土浇筑而成,其中靠近保温板一侧的钢筋网为受拉钢筋,另一侧为受压钢筋。外叶墙相比内叶墙较薄,仅一层钢筋网片,主要起整体结构的围护作用,保护保温材料,同时承担部分受力。保温板位于内叶墙与外叶墙之间,主要起保温隔热作用,连接件穿过保温板与两侧墙板浇筑相连,发挥协同作用。SIW墙板为双向板,构造对称,SIW墙板设计的构造及尺寸如图1所示,混凝土、钢筋型号分别为C30、HRB400,内叶墙钢筋直径为8 mm,外叶墙钢筋直径为6 mm,连接件截面尺寸为6 mm×10 mm、长度为115 mm。
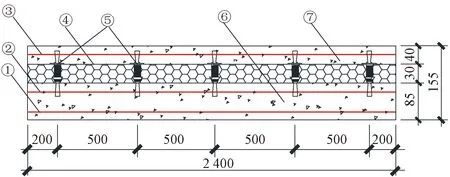
注:①内叶墙受压钢筋;②内叶墙受拉钢筋;③外叶墙钢筋;④保温板;⑤连接件;⑥内叶墙混凝土;⑦外叶墙混凝土。所有数值单位均为mm。图1 SIW墙板构造及尺寸Fig.1 SIW wall panel structure and size
1.2 建立有限元模型
以SIW墙板静载试验为参考[4],建立静力有限元分析模型,采用ANSYS有限元软件,选取八节点六面体SOLID65单元模拟混凝土内外叶墙和XPS保温板,选取两节点LINK180单元模拟钢筋、连接件,同时定义钢筋、连接件截面尺寸参数,根据图1建立模型的各参数尺寸。SIW墙板有限元模型如图2所示。采用与试验相同的加载方式和边界条件,将连接件、保温板与内、外叶墙板相交处设置为共节点,达到绑定约束的效果,在墙板侧面设置X、Y、Z3个方向的位移约束。依据GB 50320—2014《粮食平房仓设计规范》对直接接触粮食荷载的内叶墙表面施加粮食底部最不利荷载:
式中:phk为粮食作用于仓壁单位面积上的水平侧压力最大值,kN/m2;φ为粮食的内摩擦角,(°);δ为粮食对仓壁的外摩擦角,(°);γ为粮食重力密度,kN/m3;s为堆粮高度,m。粮食平房仓设计规范要求储料为小麦时内摩擦角φ取25°,外摩擦角δ取21.8°,粮食重力密度γ为8 kN/m3,最大堆粮高度s为7.2 m。
1.3 有限元分析结果验证
有限元模型采用满仓状态粮食底部有最大压力施加,经非线性模拟分析得到内、外叶墙挠度云图,如图3、图4所示,提取跨中挠度最大值、绝对值分别为2.045、2.043 mm。

注:数据单位mm。图4同。图3 内叶墙挠度云图Fig.3 Deflection of inner leaf wall
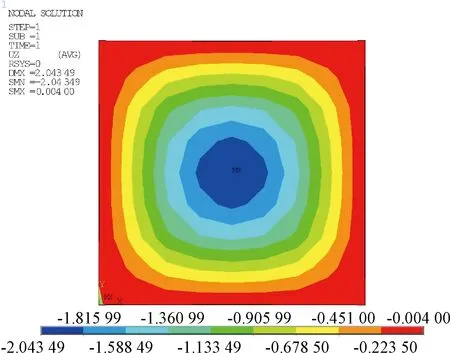
图4 外叶墙挠度云图Fig.4 Deflection of outer leaf wall
将满仓状态7.2 m堆粮高度时SIW内、外叶墙板等效粮食底部最大侧压力作用下跨中挠度试验值与模拟值对比[4],分别相差2.7%和4.2%,均不足5%,结果如表1所示,证明SIW墙板有限元分析模型是合理的。可靠性分析将以此静力有限元模型为基础,利用蒙特卡洛法将建模参数随机化,依据大量随机抽样计算,研究SIW墙板在不确定性条件下的可靠性,确定各参数对SIW墙板影响的灵敏度。

表1 跨中挠度试验值与模拟值对比Table 1 Comparison of test value and simulation value
2 可靠性分析
2.1 随机变量及分布
SIW墙板在承担粮食侧压力过程中受到不确定性的影响,主要考虑其材料性能、几何参数及粮食侧压力作用。作为一种结构组成复杂的新型构件,为研究各参数对SIW墙板可靠性的影响,优化设计参数,有必要精确地选取随机变量。本文将组成墙板厚度的6个参数均设为随机参数:外叶墙钢筋到外叶墙边缘的距离(TH1),外叶墙钢筋到保温板的距离(TH2),保温板厚度(TH3),内叶墙受拉钢筋到保温板的距离(TH4),内叶墙受拉钢筋到受压钢筋的距离(TH5),内叶墙受压钢筋到内叶墙边缘的距离(TH6)。连接件作为复合结构的关键连接材料,不仅影响结构受力,成本也较高,其间距的大小影响连接件整体布置的数量,故将其间距也设为随机变量L。钢筋半径、连接件截面尺寸也均设为随机参数。此外,组成SIW墙板所有材料的弹性模量及泊松比也被定义为随机材料特性参数。
SIW墙板虽为新型墙板,但其仍由一般基本构件组合浇筑而成,其随机变量参数的变异性仍具有普遍性。根据大数定律,在静载状态样本量很大时,数据往往趋于正态分布,且样本均值和真实均值充分接近[17]。本研究是基于粮食最不利荷载状态下SIW墙板力学性能的可靠性分析,整个结构呈静载状态,故选取随机变量服从正态分布。为保证数据可靠,均值的取值均来源于前期试验中SIW墙板的结构尺寸、材料特性,各变异系数均取自周佳乐等[11-13,18]的试验。具体各随机变量分布情况见表2—表4。
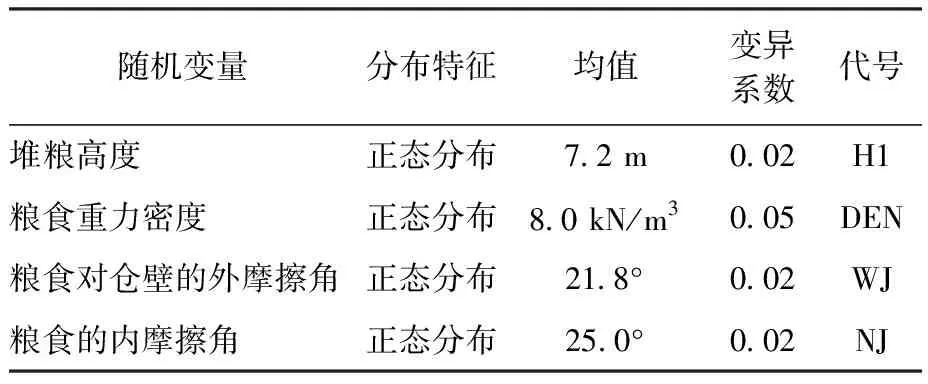
表2 荷载变量分布特征Table 2 Distribution characteristics of load variables
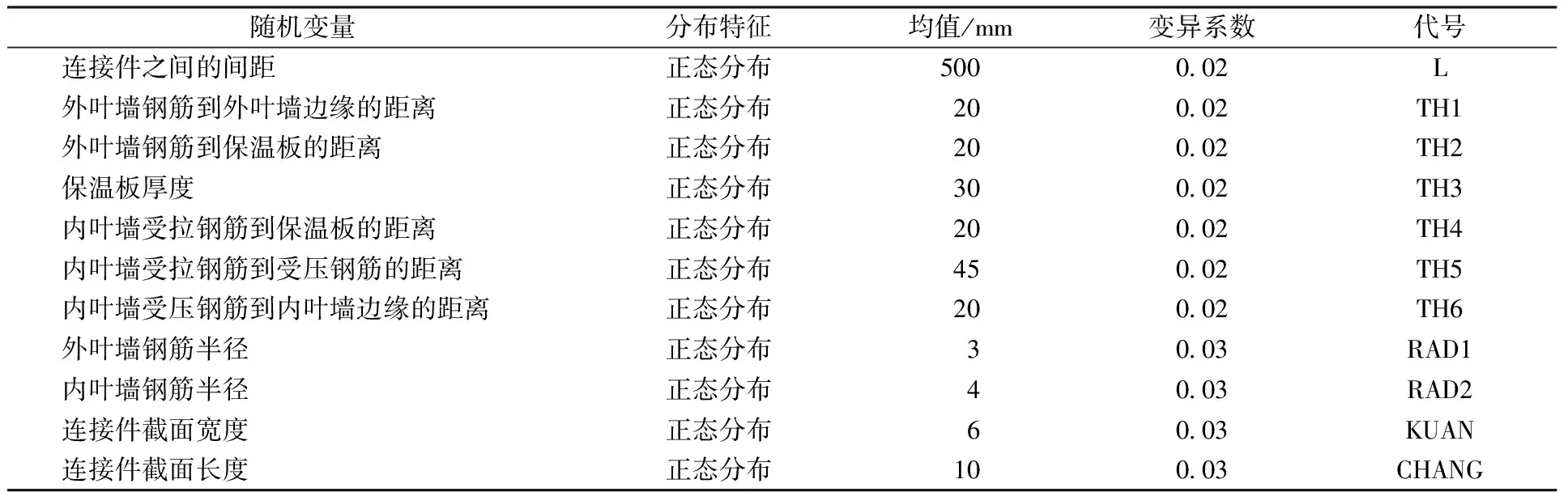
表3 几何参数变量分布特征Table 3 Distribution characteristics of geometric parameter variables
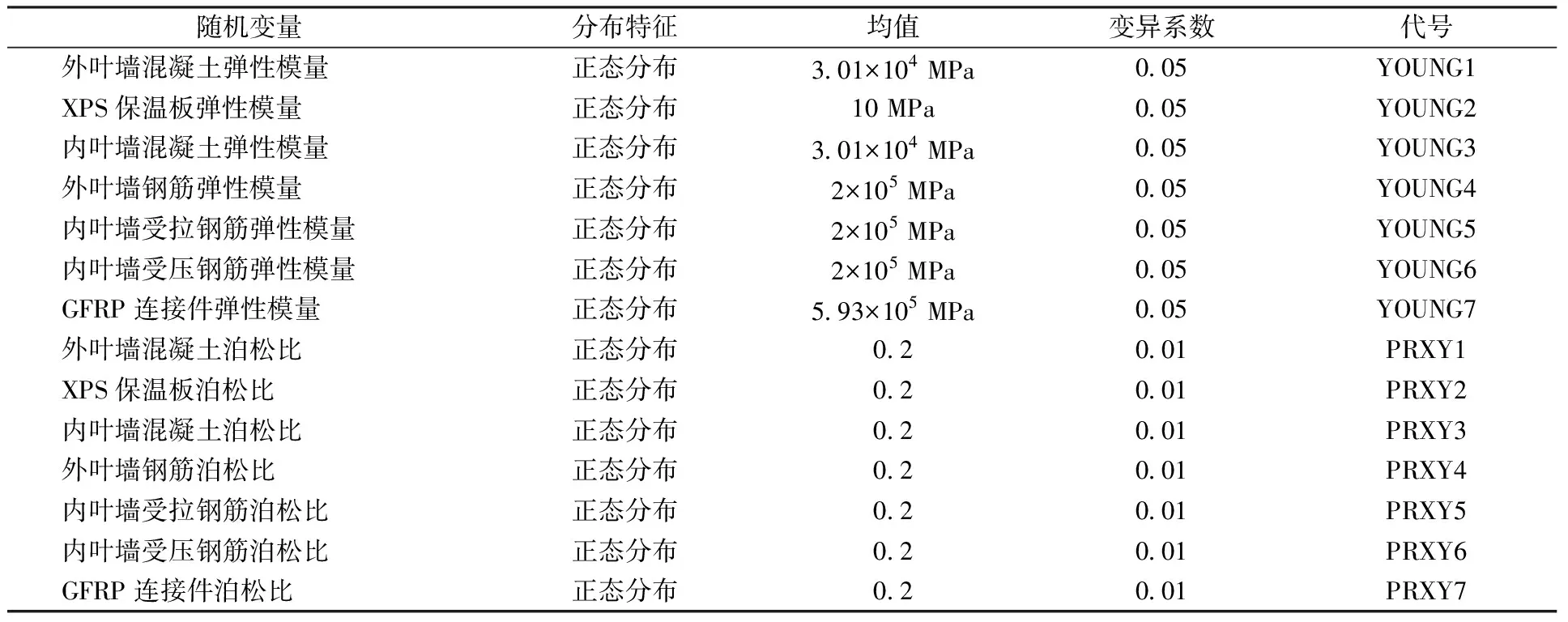
表4 材料特性变量分布特征Table 4 Distribution characteristics of material property variables
2.2 建立功能函数
依据可靠度基本理论,需建立关于SIW墙板不同控制条件下的极限状态功能函数(Z)。分析极限状态研究结构是否失效,一般常将其定义:
Z=R-S,
式中:R为抗力,S为荷载效应。
1)正常使用极限状态功能函数。SIW墙板在粮食侧压力作用下为受弯构件,根据GB 50010—2010《混凝土结构设计规范》,最大挠度δmax不应超过最大限值δlim,为l0/250(l0为计算跨度)。内叶墙挠度相比外叶墙挠度偏大,更易达到失效状态,故建立挠度功能函数(Z1):
Z1=δlim-|δmax|。
2)承载能力极限状态功能函数。SIW墙板内叶墙为主要的受力构件,混凝土应力更大[4],更容易失效,故本次研究仅考虑内叶墙混凝土强度。混凝土材料采用Hsich-Ting-Chen 4参数准则[19]建立强度功能函数(Z2):
式中:σ1、σ2、σ3分别为混凝土第一、第二、第三主应力,N/mm2;fc为C30混凝土强度,N/mm2。
2.3 蒙特卡洛随机抽样
对表2—表4所有随机输入变量采用蒙特卡洛超立方抽样方法进行100 000次随机抽样[20]。以粮食重力密度(DEN)为例,样本抽样如图5(a)所示,样本分布直方图如图5(b)所示。由图5可知,DEN抽样均值为8 kN/m3,最小值约为6.2 kN/m3,最大值约为9.6 kN/m3;图5(a)显示抽样次数为100 000次,图5(b)显示DEN服从正态分布,依据已定义随机变量的分布开展抽样,表明已抽取足够多数据支撑本次研究。
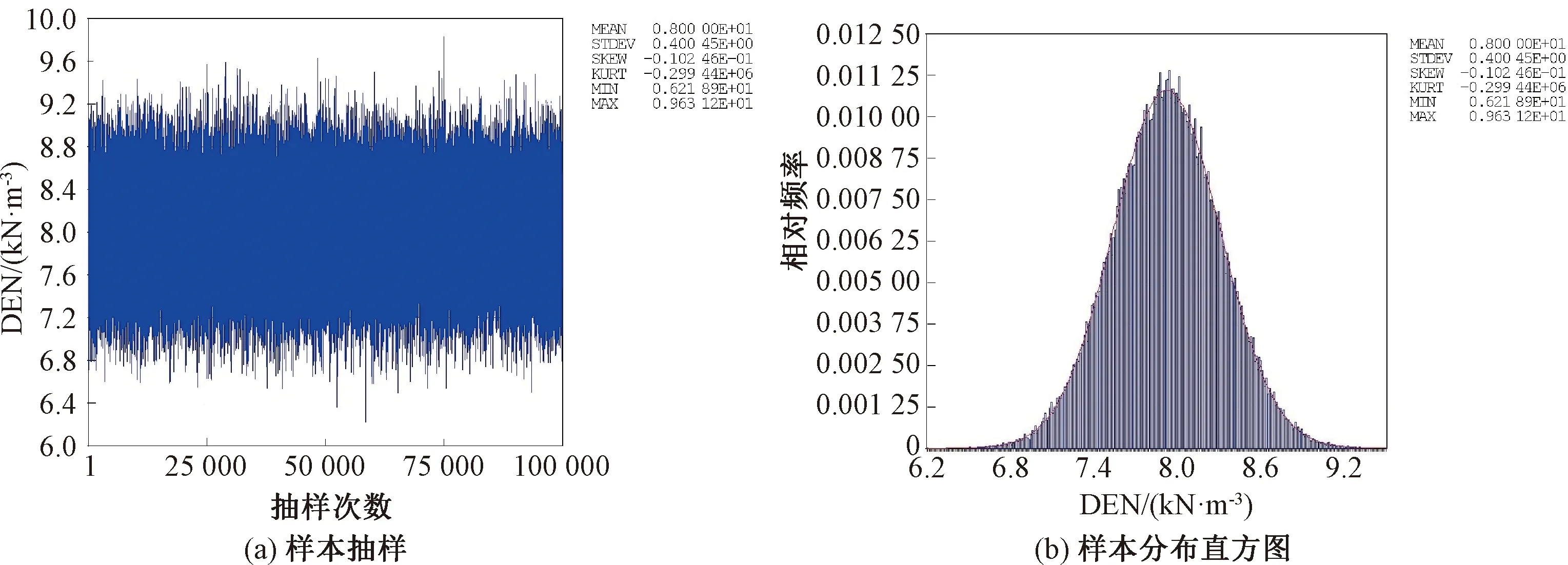
图5 DEN抽样Fig.5 DEN sample
2.4 失效概率计算
经过100 000次抽样计算,各功能函数累积分布曲线如图6所示。由图6可知,曲线光滑,无突变情况出现,表明各功能函数在95%置信区间条件下收敛性较好,置信度较高,结果准确。
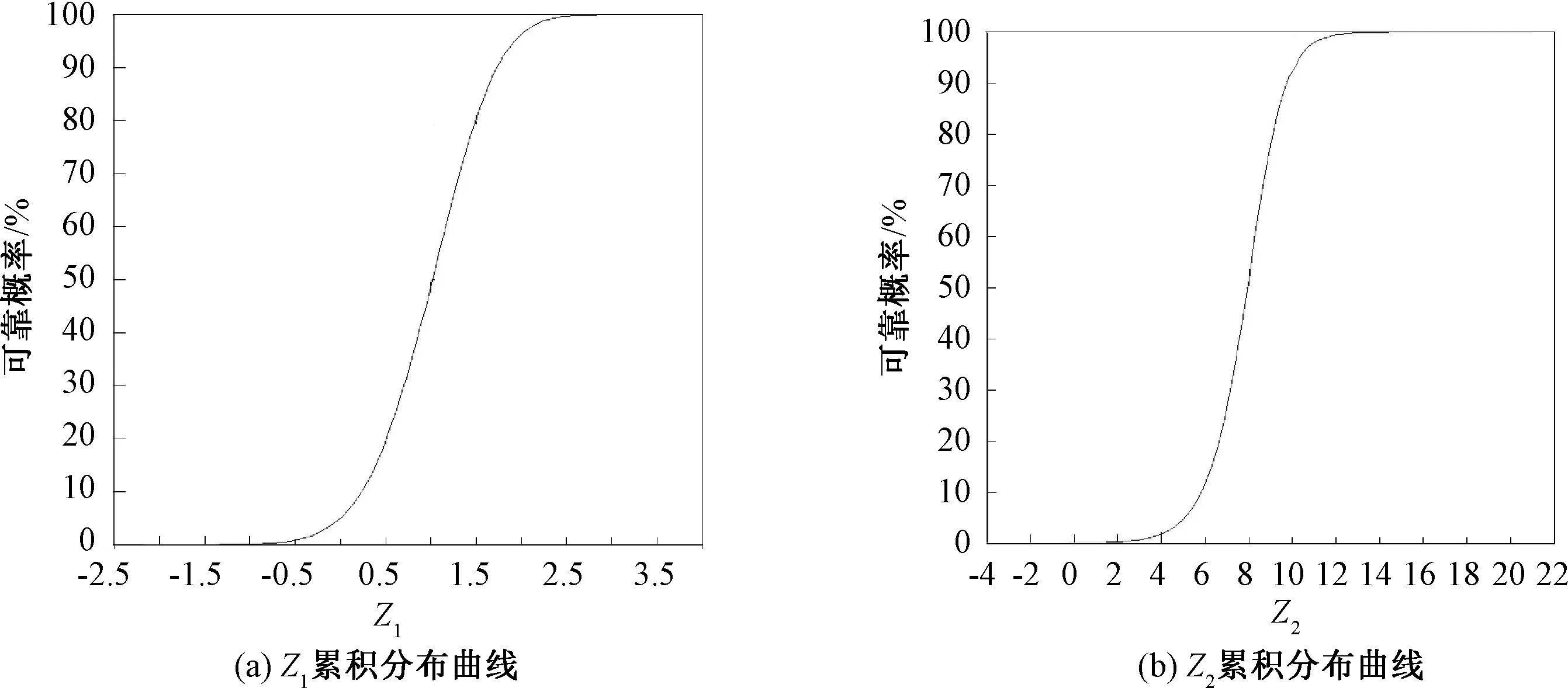
图6 各功能函数累积分布曲线Fig.6 Cumulative distribution curves of functional functions
计算结果显示,在置信度为95%的情形下,两个功能函数Zi<0(失效)的概率分别为Pf1=5.02×10-2,Pf2=3.30×10-4。根据GB 50068—2018《建筑结构可靠性设计统一标准》要求,承载能力极限状态设计安全等级为二级时发生延性破坏要求可靠指标β>3.2,正常使用极限状态的β取0~1.5即可。Pf1转化为β=1.64,Pf2转化为β=3.41>3.2,表明SIW墙板在正常使用、承载能力极限状态控制条件下的可靠指标均满足规范要求,具有较好的可靠性。
2.5 结果分析
承载能力极限状态对可靠指标的要求高,对失效概率的容许值极小,β为3.2转化为失效概率是6.87×10-4,10 000次抽样计算仅容许6.87次发生失效,这是因为承载能力极限状态控制条件下结构易失效、破坏,影响程度相比正常使用极限状态更严重,故应重点考虑影响混凝土强度(Z2)的随机参数。对Z1和Z2来说,在不同的失效准则要求下,挠度控制条件下的可靠性相比于强度更为安全,在SIW墙板结构设计中应着重关注混凝土强度对整体结果的影响,控制对影响混凝土强度较大随机参数的变异性及随机分散性,优化影响能力较大的参数值,达到提高SIW墙板混凝土强度控制条件下可靠度的目的。SIW墙板作为以钢筋混凝土为主体组成的复合结构,与普通钢筋混凝土受弯构件类似,仍需主要关注以混凝土开裂、破坏为起因的结构失效模式。
3 灵敏度及相关性分析
3.1 灵敏度分析
经抽样计算分析得到各随机参数对两个功能函数的灵敏度影响,结果如图7所示。由图7(a)可知,影响SIW墙板挠度可靠性的随机参数中DEN、YOUNG2、NJ、H1、YOUNG1灵敏度较大;由图7(b)可知,影响墙板混凝土强度可靠性的随机参数中DEN、YOUNG3、YOUNG2、TH6和TH2灵敏度较大。对灵敏度影响不明显的参数在图中不予显示。
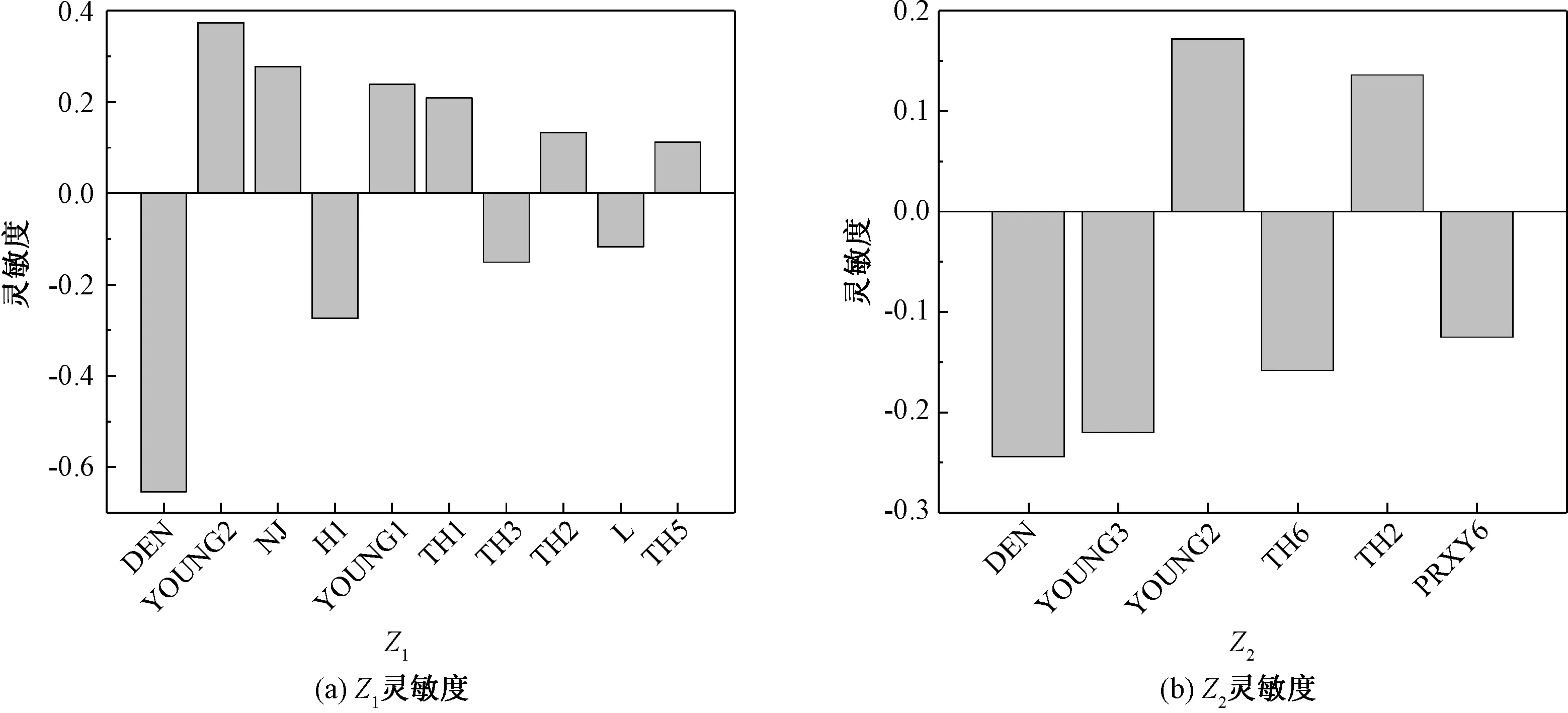
图7 各功能函数灵敏度分布Fig.7 Sensitivity distribution of each functional function
总体来看,荷载变量对SIW整体可靠性影响最大,材料特性变量次之,几何参数变量最小。灵敏度为正的参数表示对该功能函数可靠性为有利影响,相反则为不利影响。在SIW墙板结构设计、制作及应用过程中,应主要关注灵敏度较大的参数,标准化工艺流程,达到降低参数标准差及变异系数的目的,提高SIW墙板的可靠性。SIW墙板混凝土强度可靠性相对容易失效,影响其可靠性灵敏度较大的参数DEN、YOUNG3和YOUNG2中,DEN和YOUNG3灵敏度为负,对SIW墙板产生消极影响,YOUNG2为正,对SIW墙板产生积极影响。在结构设计中可适当减小灵敏度为负的参数值、适当增大灵敏度为正的参数值,达到结构优化的目的。
3.2 相关性分析
由表5可知,对应灵敏度分析结果,影响SIW墙板挠度较大的参数中DEN、YOUNG2、NJ、H1、YOUNG1的相关系数分别为-0.654、0.374、0.277、-0.274和0.239;影响混凝土强度较大的参数中DEN、YOUNG3、YOUNG2、TH6和TH2的相关系数分别为-0.244、-0.220、0.172、-0.158和0.136。

表5 相关性系数Table 5 Correlation coefficient
作为一种组成复杂的复合结构,SIW墙板在承受粮食侧压力过程中,除荷载变量的变异性之外,构件几何参数以及材料参数对可靠性的影响都较为明显。故在材料制备以及试件预制时,应严格控制一定尺寸以及材料特性标准,降低关键参数的随机分散性,可有效提高墙板的可靠度。根据相关系数的正负来分析参数对SIW墙板各条件下可靠性的积极与消极影响,结合结构优化综合考虑全部参数,在设计制作时适当地增大关键正值参数、减小关键负值参数,可达到小幅增大SIW墙板可靠度的目的。相关性分析量化了各随机参数对SIW墙板可靠性的灵敏度,通过不同参数相关系数的对比可直观地反映参数之间影响能力的差异性。
4 结论
采用蒙特卡洛随机有限元法,对粮食侧压力作用下SIW墙板开展可靠性及灵敏度分析,得到以下结论:建立了SIW墙板在粮食侧压力作用下有限元模型,并验证了其有效性,将组成其结构的参数随机化,确立了两种失效准则。经105次抽样计算得失效概率分别为Pf1=5.02×10-2、Pf2=3.30×10-4,对比规范其可靠度均在安全范围之内,故可视为SIW墙板具有较好的可靠性,应主要考虑影响混凝土强度失效较大的参数。粮食重力密度、混凝土弹性模量和保温板弹性模量是影响SIW墙板总体可靠性较为显著的参数。
