基于计算博弈的脉冲作用下航天器追逃策略

2023-09-06顾天妍张永合李超勇

上海航天 2023年4期

顾天妍，张永合，蒋峻，李超勇

（1.浙江大学电气工程学院，浙江杭州 310027；2.中科院上海微小卫星工程中心，上海 201203）

0 引言

近年来，随着航天器控制技术和轨道规划技术的不断发展，航天器空间交会技术逐渐成熟，同时能兼容的目标形式也逐渐增加［1］。当航天器双方都有自主机动能力时，传统的单边最优控制策略不再适用，航天器的交会问题可视为双边控制问题，即航天器追逃博弈问题。相较于经典控制策略，航天器追逃博弈控制同时考虑了双方的控制信息，更适用于非合作机动目标，受到国内外学者的广泛关注。

针对航天器追逃博弈问题，目前大多数学者都采用了微分对策的方法进行研究。ISAACS［2］提出微分对策论，将控制论中的部分概念和原理与博弈论结合，并应用于二人追逃问题中，初步形成了微分对策论。在此基础上，STUPIK 等［3］利用Clohessy-Wiltshire（CW）方程将航天器追逃博弈问题转化为非线性两点边值问题，并通过克里金法求解了航天器的追逃策略。针对微分对策理论方程求解困难的问题，吴其昌等［4］分别采用了遗传算法、差分进化算法和蚁群算法来求解牛顿迭代初值，从而避免复杂微分方程的求解，但这类方法的计算时间较长。此外，PONTANI 等［5］利用半直接配点方法求解异面情况下航天器追逃问题，并通过仿真验证了该方法的鲁棒性。

随着人工智能和大数据处理技术的发展，利用人工智能方法进行在线决策和规划成为可能，近年来在航天器追逃问题中的应用也逐渐受到重视。许旭升等［6］提出了一种基于多智能体深度强化学习的集群卫星空间轨道追逃博弈方法，通过多智能体深度决定性策略梯度法（Multi-agent Deep Deterministic Policy Gradient，MADDPG）训练数据，最终得到各卫星的策略。刘冰雁等［7］在传统强化学习的基础上，建立了模糊推理模型，利用分支深度强化学习有效解决了行为数量与映射规则的组合增长问题，缩短了仿真时间，提高了仿真效率。吴其昌等［8］将深度神经网络应用到航天器追逃博弈中，搭建了4 层神经网络，并通过Adam 优化算法对网络进行了训练，同时验证了最终生成策略与真实策略相近，实现了在线决策。

值得注意的是，上述文献都是针对航天器在连续时间下的连续推力模型展开，且目前大部分研究工作均在连续机动的基础上进行，针对脉冲作用下的轨道追逃博弈的研究较少，同时模型的相关研究和结论并不成熟。针对这一问题，VENIGALLA 等［9-10］提出了可达集的概念，并证明了逃逸航天器在知道追踪航天器的可达集的前提下能成功完成逃逸，给出了在共面时逃逸航天器的最优逃逸方向。LIU 等［11］研究了三人博弈问题，仅在一次脉冲机动的前提下，利用粒子群算法和牛顿插值法解决了异面最优轨迹求解问题。于大腾［12］基于序列二次优化算法建立了追踪器多脉冲最优交会模型，采用遗传算法进行了机动优化，提升了飞行器的空间生存能力。

上述方法都有效解决了航天器轨道追逃问题，但其中航天器的动力学模型由简化的CW 方程进行描述，多数没有考虑摄动力因素的影响［13］。同时，非圆轨道和较大的相对距离也是CW 方程误差的主要来源。然而航天器的实际轨迹会受到各种不可避免的摄动影响，特别是当航天器在低轨道和中轨道运行时，摄动作用力会对线性模型下的博弈结果产生不可忽略的负面影响。因此，本文旨在解决地球高阶引力模型下，基于脉冲控制的航天器轨道追逃问题，并通过计算博弈进行求解。

在计算博弈问题中，快速搜索（Action-Reaction Search，ARS）算法能够高效求解纳什均衡点。针对多组动态武器目标分配（Multi-team Dynamic Weapon Target Assignment，MDWTA）生成矩阵规模较大的问题，GALATI［14］提出利用ARS 算法沿最优方向搜索，有效利用内存，提高计算可行性。剪枝算法常用于减少算法搜索时间和提高计算效率，REED［15］提出利用剪枝算法应用于神经网络中以减少不必要的搜索路径，至今剪枝已经分化出多种类别，包括结构化剪枝和非结构化剪枝等，应用于计算机［16］、电气［17］、航空航天［18］等领域。

本文提出了一种基于计算博弈的控制策略，通过优化航天器的速度增量大小和方向，实现了追逃双方的性能指标最优化。本文的主要工作：1）完成了航天器轨道追逃博弈问题的数学定义，其中性能指标函数考虑博弈双方的距离和燃料消耗，并以速度增量大小和方向构建容许控制集；2）创新性地引入ARS 算法，并将一种数据剪枝策略嵌入，从而保证了纳什均衡解的准确性以及求解速度。本文证明了在逃逸航天器没有机动的情况下，该算法可以成功地将轨道追逃博弈问题转换为最基本的航天器轨道交会问题。仿真结果验证了本文方法的有效性和可行性。

1 问题描述与数学建模

假设在航天器轨道追逃任务场景中，追击航天器预先通过Hohmann 转移拦截目标航天器，但在通过第一次机动之后，目标航天器可通过施加一个微小偏移脉冲规避追击航天器的拦截。此时，双方各自有一次施加脉冲机动的机会，且在同一时刻机动。追击航天器需要在燃料消耗尽可能小的情况下拦截逃逸航天器，而逃逸航天器则需在燃料消耗尽可能小的情况下规避拦截。

1.1 航天器动力学建模

在航天器追逃博弈问题中，为了便于计算和分析，采用J2000 下的地球惯性坐标系。考虑到摄动力等因素，航天器的动力学模型为［19］

式中：r为航天器的位置矢量；v为航天器的速度矢量；U为地球的引力势函数。

当地球为旋转椭球体，且只考虑J1至J6摄动项时，令地球赤道半径为Re，则地球引力势函数可以简化为

式中：μ为地球引力常数；J2=1.082 6×10-3，J3=-2.536×10-6，J4=-1.618 6×10-6，J5=-0.226×10-6，J6=0.539×10-6；P2～P6为勒让德多项式，表达式如下：

在施加脉冲作用的时刻，航天器的状态变化为

式中：上标“-”和“+”分别为脉冲作用前后的状态。

在J2000 坐标系下，式（4）可以扩展为

式中：φ为脉冲推力偏角；γ为脉冲推力仰角。

1.2 博弈问题构建

自20 世纪以来，航天器的交会对接技术在工程应用及理论研究中具有重要意义，有许多突出成果，其中Hohmann 转移［20］和Lambert 追击［21］是最为经典的方法。Hohmann 转移方法给出了共面下轨道转移的最小能量消耗，奠定了之后大多数理论的基础，但是存在调相时间过长，耗费时间巨大的问题；Lambert 追击方法计算了固定时间下两点之间轨道转移所需脉冲。上述理论均要求目标航天器被动飞行且没有自主机动，不适用于目标存在自主机动的航天器追逃博弈问题。在航天器追逃博弈问题中，追击航天器和逃逸航天器通过控制自身的脉冲机动，使得双方的性能指标函数达到最优，即：

式中：下标P、E 分别为追击航天器和逃逸航天器。

航天器的追逃博弈问题包含3 个要素：博弈参与者{P，E}；双方各自的性能指标函数J；以及参与者的行为策略(uP，uE)。

追击航天器的行为策略uP定义为

上式中各项满足如下约束条件：

针对上述航天器追逃博弈问题，SCHEERES等［9］基于可达集的概念推导了逃逸航天器的最优逃逸方向，耿远卓等［22］利用终端诱导强化学习对航天器追逃博弈问题进行了求解，通过在奖励函数中考虑终端误差从而提高追击成功率。然而，这些航天器通常采用二体模型或CW 方程进行求解，没有考虑地球摄动因素影响，且对轨道形状有所限制，所得结果精度不足。为了满足实际情况，提升求解模型的精度，本文采用计算博弈的方法来解决航天器追逃博弈问题。

与传统的以解析形式求解博弈双方纳什均衡点的方法不同，计算博弈通过对双方的策略进行数值搜索，得到双方各自的最优解。此外，追逃航天器的性能指标函数J包含两部分，分别由追逃双方的距离以及各自消耗的燃料定义。双方博弈的目的是通过给出自己的脉冲控制策略，使得相应的性能指标函数最大化。具体来说，对于追击方而言，其期望在尽量减少燃料消耗的情况下减少追逃双方距离；对于逃逸方而言，则期望自己在尽量减少燃料消耗的情况下增加追逃双方距离。因此，性能指标JP和JE定义如下：

权重系数应满足以下条件：

追逃航天器双方的距离L定义如下：

当逃逸航天器中途没有脉冲机动，则追逃问题就会转化为普通的轨道交会问题。此时，双方的性能指标函数也相应变化。对于追击方而言，性能指标如下：

对于逃逸方而言，性能指标JE如下：

本文所定义的追逃博弈问题就是寻找追击航天器者和逃逸航天器的纳什均衡点问题，使其指标函数大于任意其余策略的指标函数，纳什均衡点的定义如下：

式中：UP、UE分别为追击航天器和逃逸航天器的所有策略。

对于追逃航天器双方而言，可供选择的策略是有限的，由纳什均衡的存在性定理［23］可知，每一个有限的策略式博弈至少存在一个由式（14）描述的纳什均衡解。那么最终求得的纳什均衡解所对应的速度增量大小和方向就是当前问题的一个可行解。

通过计算式（16）中的矩阵解可以求得纳什均衡点。决策矩阵式（16）存在维数大、计算时间长和搜索效率低的问题，为了解决这一问题，本文采用ARS 算法来求解博弈矩阵。

2 基于计算博弈的快速优化策略

为了求解追逃双方的纳什均衡点，使得双方的性能指标函数处于最优，本文采用ARS 算法［24］来进行快速求解，具体算法流程如下。

2.1 算法1：Action-Reaction Search

2.2 算法2：数据剪枝方法

与穷举法相比，ARS 算法无需对整个矩阵进行遍历，能够有效地减少计算维度，具有计算效率高、时间快的优点。对于航天器追逃博弈这一问题而言，实时性和快速性尤为关键，也为ARS 算法的使用提供了有力依据。

博弈决策矩阵式（16）中会存在不满足实际约束的策略对，ARS 算法同样也对这些策略进行了搜索，增加了计算时间，使搜索效率降低。因此，本文提出了一种剪枝方法，在矩阵生成和搜索过程中，对无需计算的元素进行标记剪枝，剪枝流程如下：

输入：追逃博弈双方的策略集合UP=[ΔvP，φP，γP]，UE=[ΔvE，φE，γE]，收益维度M、N；

输出：无需计算的矩阵元素标记集合Apruned；

算法2 通过对冗余不必要的数据进行剪枝，减少了不必要的搜索过程，提高了搜索速度和运算效率。

本文通过使用ARS 算法准确寻找纳什均衡点，ARS 算法通过对单独的行列寻找来避免搜索整个矩阵，极大地提高了运行效率。本文采用剪枝技巧来提升寻找纳什均衡点的计算速度，通过对冗余数据的剪枝达到缩小矩阵规模的目的，从而加快数值搜索进度。

为了更直接地说明基于剪枝的快速搜索方法的优越性，将其与穷举法、α-β剪枝［25］进行对比。在进行不同维度的矩阵计算时，双方求解纳什均衡点的时间如图1 所示。

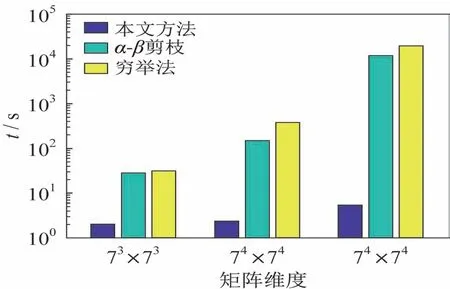
图1 决策时间对比Fig.1 Comparison of decision time

由图1 可知，相比于其他方法，本文所采用的快速求解算法能有效提高计算效率，节省计算时间。当矩阵维度扩大时，其余方法的仿真时间以指数形式增长，而本文方法增幅不大，仍能快速寻找到纳什均衡解。

3 仿真分析

3.1 轨道交会算例分析

当逃逸航天器不施加机动时，追逃问题演变为轨道交会问题。本文采用硬件平台为3.60 GHz AMD Ryzen 5 3500X 处理器，软件平台为 Matlab R2022b 进行仿真。为了便于比较，将追击航天器的初始机动时间与Hohmann 转移的时间一致。两航天器初始轨道六根数见表1。

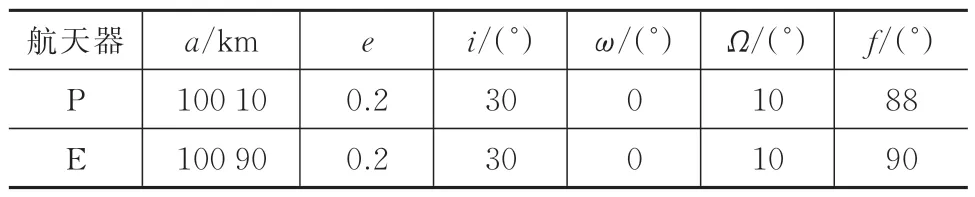
表1 交会场景下航天器的初始六根数Tab.1 Initial six parameters of the spacecrafts in the rendezvous scenario

两航天器飞行轨迹如图2 所示。

图2 交会场景下航天器三维空间飞行轨迹Fig.2 Trajectories of the spacecraft in the rendezvous scenario

为进一步验证本文方法的有效性，分别与Hohmann 转移和Lambert 追击进行对比，三者都在同一时刻进行第一次脉冲机动，且都施加两次机动，一致采用地球高阶引力模型。追击航天器与逃逸航天器相对距离如图3 所示。

图3 交会场景下航天器相对距离Fig.3 Relative distance of the spacecraft in the rendezvous scenario

3 种方法的最终计算结果见表2。其中，追击航天器均在T1=3 172.590 5 s 时施加第1 次脉冲机动，第1 次速度增量大小为Δv1，第2 次机动时刻为T2，第2 次速度增量大小为Δv2。

表2 交会场景下航天器仿真结果Tab.2 Simulation results of the spacecraft in the rendezvous scenario

由表2 可知，与Hohmann 转移相比，本文方法的脱靶量明显较小，但稍逊于Lambert 追击。本文方法在保证脱靶量的情况下，使用速度增量明显小于Lambert 追击，有效减少了燃料消耗。此外，在进行计算时，本文方法无需选定初值，避免了采用其他2 种方法在初值选定不正确时可能存在的不收敛和脱靶量大的问题。

3.2 追逃算例分析

当逃逸航天器施加机动时，两者是典型的追逃问题。在追击航天器采用Hohmann 转移施加第一次机动后，双方都还有一次脉冲机动机会，逃逸航天器施加脉冲推力逃离追击航天器，双方在这一时刻通过矩阵搜索都使彼此性能指标函数达到最优。

根据Hohmann 转移计算易得，追击航天器第一次机动时刻T1=3 172.590 5 s，施加速度增量大小Δv1=0.031 1 km/s。此后，逃逸航天器施加控制量试图远离追击航天器，双方展开追逃博弈。设置追击航天器最大可使用速度增量=0.061 0 km/s，逃逸航天器最大可使用速度增量=0.008 0 km/s。两航天器飞行轨迹如图4 所示。

图4 追逃航天器三维空间飞行轨迹Fig.4 Three-dimensional space flight trajectory of the spacecraft in the pursuit-evasion game

两航天器使用燃料情况和脱靶量见表3。通过仿真可知，追击航天器使用了全部速度增量ΔvP=0.061 0 km/s，偏角φP=199.998 4°，仰角γP=-5.998 4°。逃逸航天器也使用了全部速度增量ΔvE=0.008 0 km/s，偏角φE=270°，仰角γE=-5.998 4°。两航天器距离从最开始的364.95 km 缩短到最终脱靶量4.32 km。当采用这种策略时，双方的性能指标函数都达到最优。