Features of transport induced by ion-driven trapped-electron modes in tokamak plasmas
2023-09-05HuiLi李慧JiQuanLi李继全FengWang王丰QiBinLuan栾其斌HongEnSun孙宏恩andZhengXiongWang王正汹
Hui Li(李慧), Ji-Quan Li(李继全), Feng Wang(王丰),†, Qi-Bin Luan(栾其斌),Hong-En Sun(孙宏恩), and Zheng-Xiong Wang(王正汹),‡
1Key Laboratory of Materials Modification by Laser,Ion,and Electron Beams(Ministry of Education),School of Physics,Dalian University of Technology,Dalian 116024,China
2Southwestern Institute of Physics,Chengdu 610041,China
3Faculty of Electronic Information and Electrical Engineering,Dalian University of Technology,Dalian 116024,China
Keywords: drift waves,nonlinear phenomena,plasma simulation
1.Introduction
Turbulent transport seriously impacts and restricts plasma confinement performance in magnetic fusion reactors.[1–3]In high-temperature fusion plasma, the energy transport across magnetic field lines including the particle and thermal transport greatly depends on the collective modes in regimes of the collisional mean free path longer than the relevant magnetic connection length.As one of the major issues in fusion plasma,disruptions are extremely dangerous.In the tokamak,as a well-known conception of disruption,the plasma can suddenly escape the confinement.This abrupt loss of confinement causes thermal and magnetic loads on the walls,as well as the potential formation of electron currents with relativistic energies,which can seriously damage the devices.To be a viable design for a fusion power plant, the tokamak must be able to avoid, or at least reliably mitigate, the effects of disruptions.Even without a power plant, the requirement of minimizing disruptions in ITER is essential.[4–6]Because the avoidance and mitigation techniques are inherently more effective when more warning time is provided for them to be implemented,much more attention has been paid to the disruption prediction.
It has been accepted that the magnetohydrodynamics(MHD)instabilities are related to the disruption.[7,8]Currentdriven magnetohydrodynamics(MHD)instabilities,which are known as relating to the magnetic reconnection, are usually observed in both laboratory and space plasmas.However, it is unclear how the macro-scopic current-driven instabilities can couple to the microscopic magnetic reconnection,previous researches in the theory and simulation have revealed that the cascade via a transition of successively smaller scale current-driven instabilities is possible.In the previous experimental and numerical researches, the results demonstrate a viable path from macro-scale MHD physics to microscale non-MHD physics associated with the occurrence of fast reconnection.[9]In the last decade, the increasement of interest in the interaction between turbulence and MHD phenomena has occurred in the fusion device plasmas, both experimentally and theoretically.[10,11]The sawtooth and neoclassical tearing modes(NTMs)essentially dominate the core MHD activity.[12,13]The latter one can be made unstable by the current or nonlinearly seeded by the turbulence, edge localized modes(ELMs),or internal kink mode crashes.
Particularly in plasma core, much of the transport is due to the turbulence induced by the ion temperature gradient(ITG) mode and trapped electron mode (TEM).[14–16]Meanwhile, a critical physical model is built numerically to illustrate the anomalous particle convection reversal caused by ITG and TEM instabilities.[17]It has been generally recognized that ITG and TEM are responsible for the ion and electron transport, respectively.[18,19]However, there are interesting and important differences between these modes in tokamaks and stellarators.Several tokamaks,such as the Tore Supra,[20]KSTAR[21]and HL-2A devices,[22]have shown the evidence about the transition of turbulence including the ITG and/or TEM.The anomalous transport caused by micro-turbulence has been revealed recently including both in H-mode[23,24]and L-mode[25]plasmas.In additional, several physical effects,including the collisions,magnetic shear,finiteβand finite Larmor radius effects[26–32]and other plasma parameters are considered as well.Furthermore, the turbulent transport is determined by the type of micro-turbulence[33,34]and it has been illustrated in the experiments, theories and simulations.Additional, transitions of turbulence in plasma density limits were discussed.[35]It is worthy to note the turbulent transport may also have influence on plasma disruptions,such as heavy impurity concentration to core region.TEM may adjust the heavy impurity pumping out.
The ubiquitous mode, as an important branch of trapped electron modes(TEMs),is a favored topic for studying anomalous energy transport in the fusion plasmas.On the one hand,typical TEMs have moderated to long wavelengths that propagate with the direction of electron diamagnetic drift.On the other hand, another essential branch of TEMs related to thebi≡/2≫1 is defined as the ubiquitous mode,which propagates in the direction of the ion diamagnetic drift
The purpose of this research is to present the physics of the ubiquitous mode in the collisionless plasma, which can result in relatively strong anomalous plasma diffusion.More precisely, the parameters of the ubiquitous mode in tokamak plasmas are illustrated with simulations in this work based on the gyrofluid equations of drift waves in inhomogeneous plasmas.At first, we confirm the majority of theoretical predictions made about ubiquitous mode,two of which are the proof that ubiquitous mode exists in tokamaks and the proof that the magnetic drifts of both trapped ions and electrons are the real driving forces behind the ubiquitous mode.Finally, the findings demonstrate that ubiquitous mode is typically inevitable in the tokamak plasmas with various parameter regimes and that their greater development rates are what cause ubiquitous mode to contribute to the electron transport.These findings will have an influence on the revealing of the characteristics of ubiquitous mode in tokamaks.Simulations are used to investigate the space of profiles withTe/Ti=1.Finally,the results show a transition between the ion temperature gradient(ITG)instability and TEM, associated with a stability valley of the growth rates with significantly reduced growth rates.
The remainder of the paper is organized as follows.The physical model with relevant equations and the simulation setting will be introduced in Section 2.In Section 3,the numerical linear and nonlinear results will be brought in and systematically analyzed.The electrostatic stability map is presented in this section as well.In Section 4, we will provide a summary of our findings as well as some discussions.
2.Physical model and simulation setting
To simulate the time evolution of the ion-driven trappedelectron mode and understand the underlying mechanism of the nonlinear turbulent transport,a set of five-field fluid equations is advanced based on the Weiland model[40]here.The effects of both the Landau damping effect[41–43]and the nonadiabatic response of trapped electrons are included in this model for describing the evolution of global electrostatic ITG and TEM turbulence through exploiting the extended fluid code (ExFC) based on the so-called Landau–Fluid model as follows:
wherene,Te,Ω,υ‖andTiare the normalized electron density,electron temperature, vorticity, parallel ion velocity and ion temperature,respectively,with the operatorsdt f=∂t f+[φ,f]and [φ,f]=r−1(∂rφ∂θ f −∂θφ∂r f).Here,frepresents any field variable.ς=5/3 represents the adiabatic compression index.The diffusivity terms are set asDn=DTe=DU=Dυ=DTi=4.8×10−3.
The other operators are written asωdte= 2ελtqr−1∂ϕ,ωdi=2ε(cosθr−1∂θ+sinθ∂r)andλt=1/4+2s/3,namely,the trapped electron precession drift operator,the ion magnetic drift operator and the dependence of the precession frequency of trapped electron on the magnetic shears=rdq/qdr, respectively.Andε=a/Ris the inverse aspect ratio.The fraction of trapped electron isand the passing electron is set asfc=1−ft.The parallel velocity of trapped electron is set as homogenous.In ExFC code, the real frequency of the TEM is positive.
The normalization of the gyroBohm type is as follows:
where the ion sound gyroradiusρs0=mics0/eiB0and the ion sound speedcs0=(Ti0/mi)1/2.The unit of the transport coefficient isρcs0/a.The ratios of the temperature and density are shown as
The equilibrium quantity in unit of arbitrary reference value is represented by the subscript label with 0.

the temperature profiles
and the safety factor
Here, the subscript labelsstands for the species of electron and ion, the label c corresponds to the plasma center with magnetic axis.The other parameters arer0=0.5aand∆r=∆rs=0.15a.Further details and benchmarks of the ExFC can be found in our previous work as Refs.[44,45].In the following simulation,except for the additional statementTe∼Tiandηi≈ηe=0.4.
3.Numerical simulation and modeling analysis
3.1.Parameter dependence
In this section,we discover the TEMs with two branches by examining the wavenumber spectra of low frequency drift waves through the gyro-fluid simulations.In the lowerkθregime, the real frequencyωis positive indicating a typical TEM branch propagating with the electron diamagnetic drift direction as shown in Fig.2.However,in the higherkθregime,the real frequency turns into negative regime which represents the instability is in the ion diamagnetic drift direction.The tokamak parameter, such as the inverse aspect ratioε, influences the appearance of the ubiquitous mode and the intensity of the instabilities.It is obviously displayed in Fig.1 in which the growth rates are enhanced with the increment of theε.The threshold of the ubiquitous mode is influenced as well.It is suggested that the toroidal number for the ubiquitous mode excited drops significantly associated with the inverse aspect ratio increasing.The result implies that it is easy for the TEM changing into the regime of ubiquitous mode with the increasement of the fraction of trapped electrons.Similar result is displayed in the research[39]with gyrokinetic simulations.With further searching, the nonlinear transports are displayed.
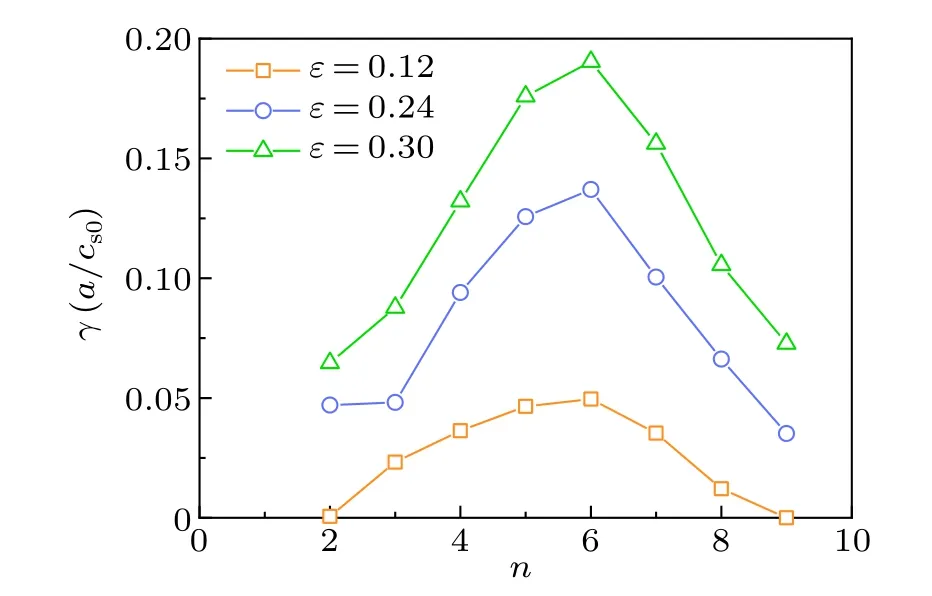
Fig.1.The normalized growth rate with the functions of toroidal wavenumber n as ε =0.12,0.24 and 0.3.
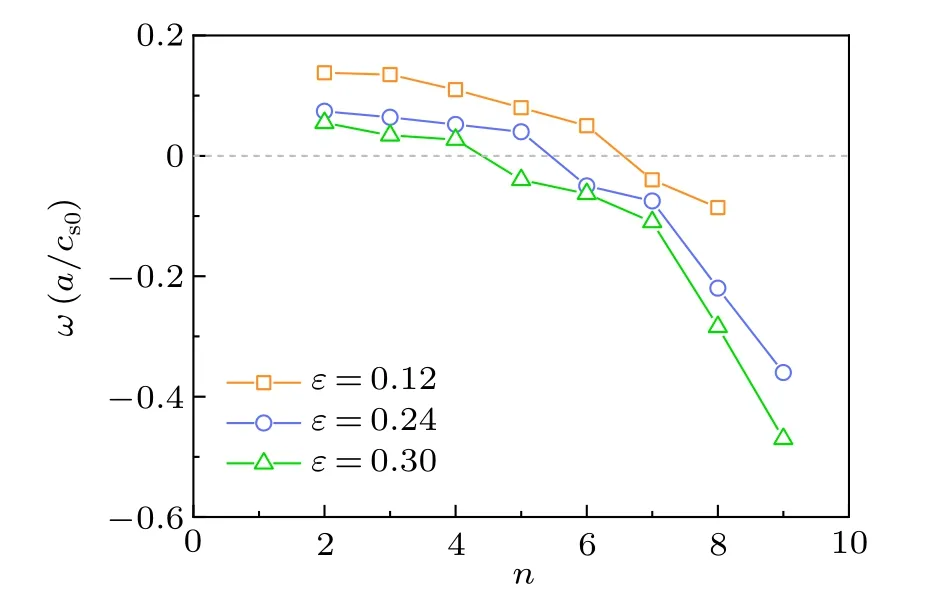
Fig.2.The normalized frequency with the functions of toroidal wavenumber n as ε =0.12,0.24 and 0.3.
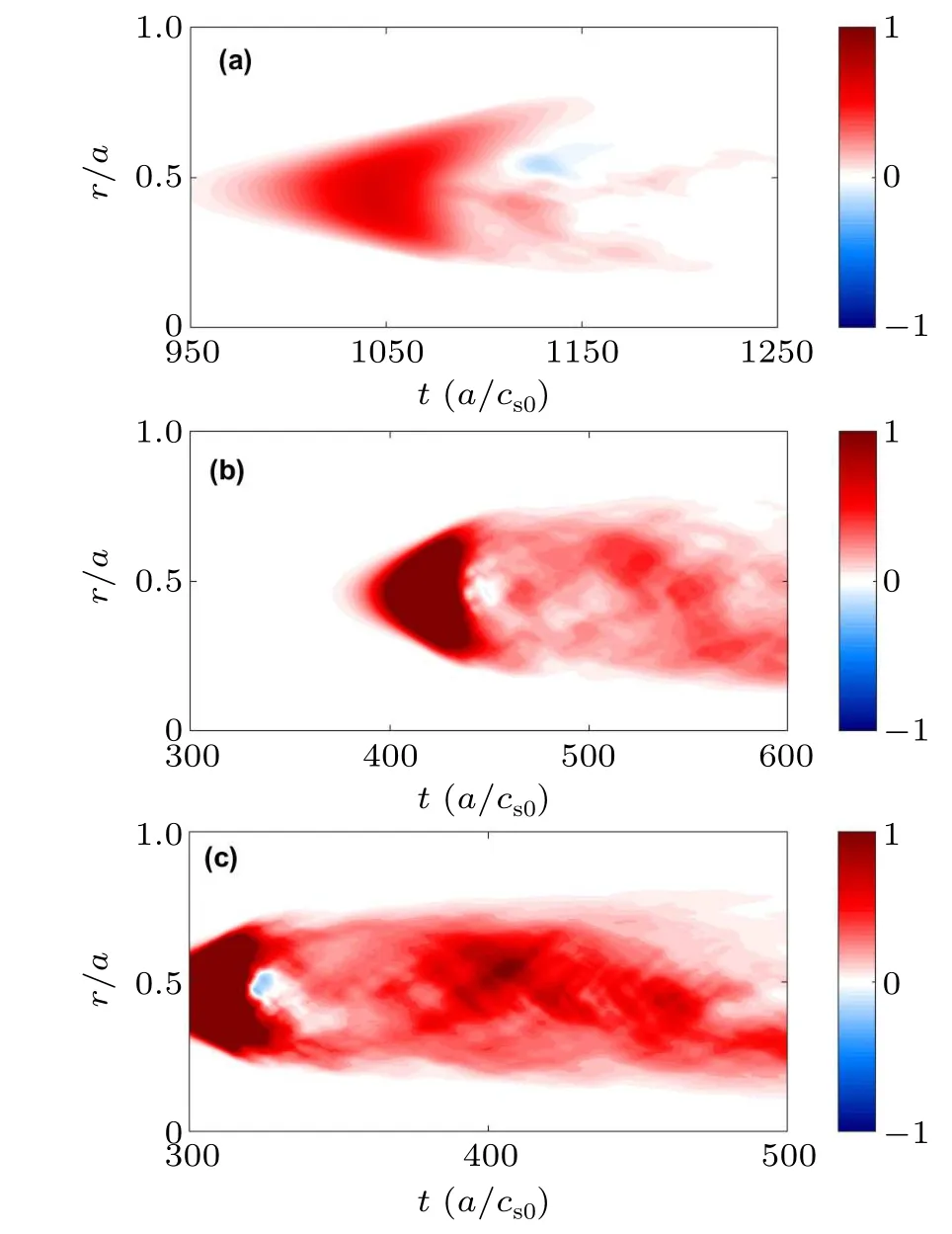
Fig.3.Time evolution of radial particle flux Γ with(a)ε =0.12,(b)ε =0.24 and(c)ε =0.3.

Fig.4.Time evolution of ion heat flux Qi with(a)ε=0.12,(b)ε=0.24 and(c)ε =0.3.
As introduced in Section 1, the ubiquitous mode can cause relatively strong anomalous diffusion especially for the heat diffusions.Here,for instance,the evolutions of ion particle fluxΓand heat fluxQiare displayed in Figs.3 and 4.The outward particle flux is greatly enhanced as theεincreases.For the heat flux, the similar character is revealed.However,it is more localized for the heat flux compared with the particle flux.The effect of another plasma parameter,ηe, is also researched.Figures 5(a)and 5(b)represent that the ubiquitous mode has a threshold value and it increases with increasingηe.It can be concluded that the typical TEM occurs with largerηe.In other words,withηeincreasing,the ubiquitous mode turns into the typical TEM.It can be concluded that the higherεand lowerηeare beneficial for the occurrence of the ubiquitous mode.
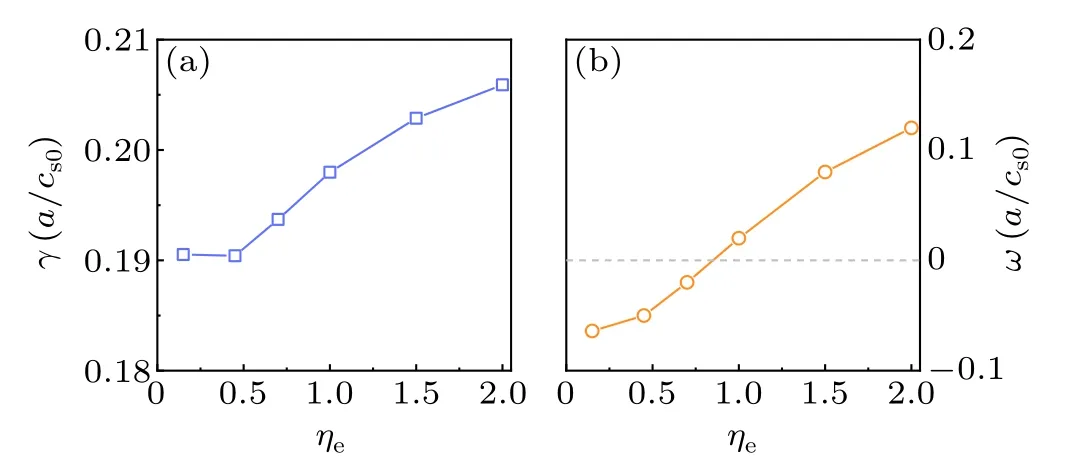
Fig.5.(a)The normalized growth rate and(b)the normalized frequency with the functions of ηe with toroidal wavenumber n=7.
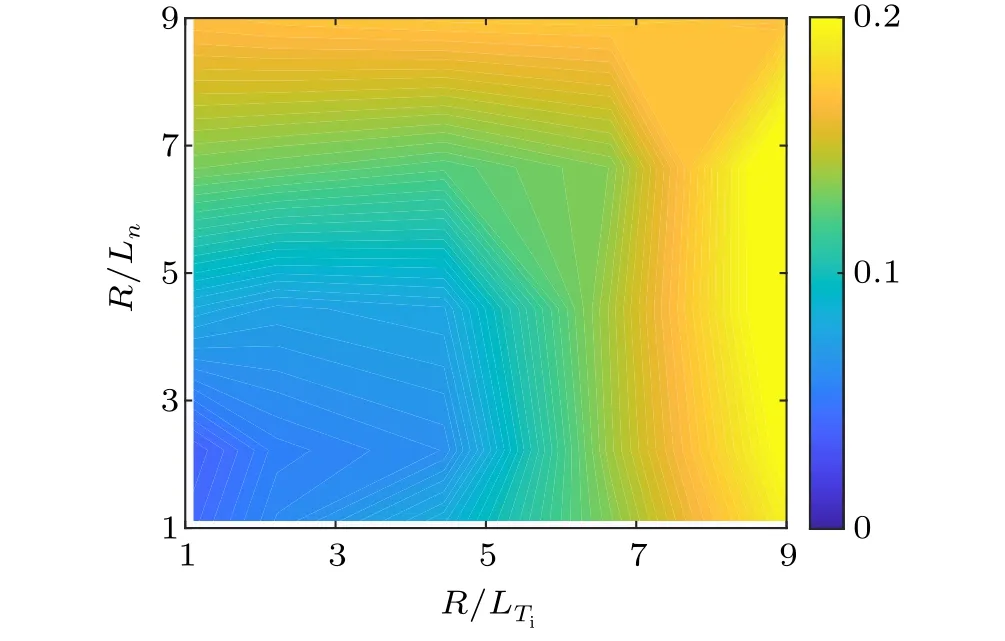
Fig.6.Diagram for th(e growth rate of dom)inant instability depending on three key parametersR/Ln,R/LTe,R/LTi.Here,R/LTe =R/LTi.
Here, the electrostatic stability map is presented as displayed in Fig.6.The map is created with plotting the growth rateγof the most unstable mode.The simulations are scanned with ion temperature gradientR/LTiand density gradientR/Ln.The temperature gradients of ion and electron are set as equal,namelyR/LTi=R/LTe.In the Fig.6,TEM is dominant on the top-left whereR/Lnis greater thanR/LTi.In the regionR/LTi Fig.7.Growth rates as a function of R/Ln.The dashed lines are R/Ln =4.4 (blue), R/Ln =6.6 (green) and R/Ln =8.8 (orange).Here,kθ =0.34 with R/LTi =R/LTe. We investigate the properties of ubiquitous mode corresponding to the TEM using gyro-fluid simulation in collisionless plasmas.It is critical in revealing the anomalous transport.The ubiquitous mode obviously occurs in tokamaks which are provided by the findings.It is found that the ubiquitous mode drifts in the ion diamagnetic direction with short wavelength.It is displayed that the wavenumber for the ubiquitous mode changed into typical mode is influenced by the parameters.Furthermore, the ubiquitous mode may play essential roles in turbulent transport as well.Then,we investigate a region of the electrostatic instability space with the assuming ofR/LTi=R/LTe.The growth rate decreases around the regionηi≈1 as theR/Lnincreases accompanied with the coexistence of ITG and TEM.When the appropriate profile requirements are satisfied, the valley can create opportunities for operation with decreased losses associated with the assumption of the suppression of the micro-instabilities results in lower turbulent transport. Acknowledgments Project partially supported by the National Natural Science Foundation of China (Grant Nos.12205035 and 11925501) and also partially by the National Key Research and Development Program of China (Grant Nos.2017YFE0301200 and 2017YFE0301201).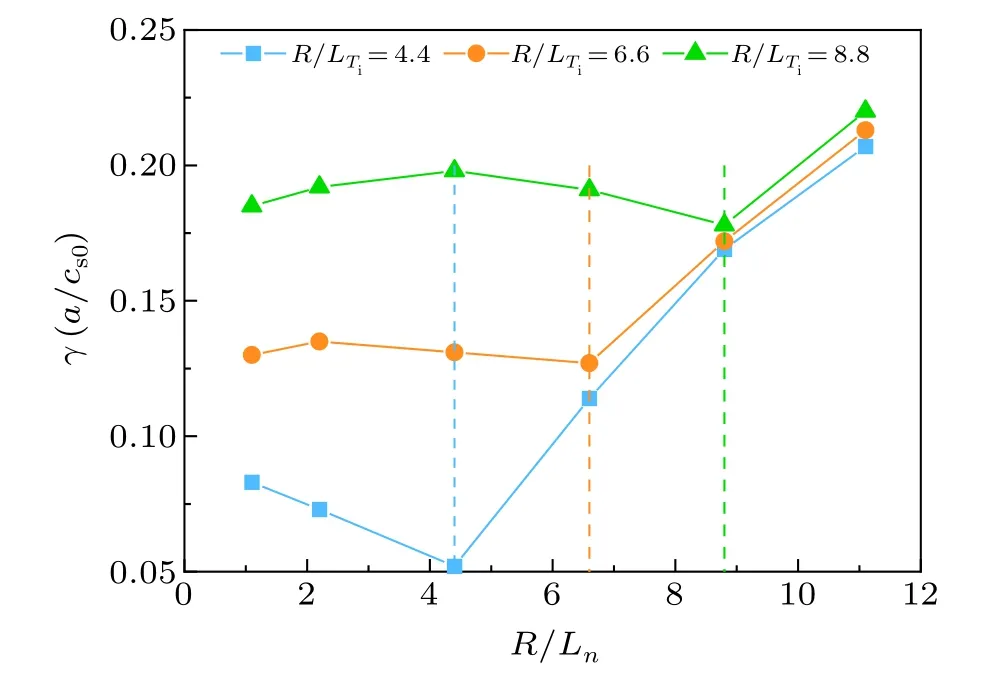
4.Summary
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Optimization of communication topology for persistent formation in case of communication faults
- Energy conversion materials for the space solar power station
- Stability of connected and automated vehicles platoon considering communications failures
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing
