Optimization of communication topology for persistent formation in case of communication faults
2023-09-05GuoQiangWang王国强HeLuo罗贺XiaoXuanHu胡笑旋andJianWeiTai台建玮
Guo-Qiang Wang(王国强), He Luo(罗贺),†, Xiao-Xuan Hu(胡笑旋), and Jian-Wei Tai(台建玮)
1School of Management,Hefei University of Technology,Hefei 230009,China
2Key Laboratory of Process Optimization&Intelligent Decision-making,Ministry of Education,Hefei 230009,China
3Engineering Research Center for Intelligent Decision-making&Information Systems Technologies,Ministry of Education,Hefei 230009,China
Keywords: persistent formation, communication topology, formation communication cost, communication fault
1.Introduction
Agent formation has been widely used in many fields, such as large-object transportation,[1]mobile target tracking,[2]and earth observing.[3]To maintain the formation shape, there are mainly the following three formation control methods: position-based,[4,5]displacement-based,[6,7]and distance-based[8,9]methods.In comparison with other methods, the distance-based method has the advantage of requiring no knowledge of the orientations of the agents in global coordinates.[10]Agent formation using distancebased method can be further divided into two categories:rigid formation[11,12]and persistent formation.[13,14]Compared with the rigid formation, the persistent formation only needs to use half of the communication links.[15]
In a persistent formation, one agent usually acts as the leader and tracks a predetermined reference trajectory, and the other agents receive the information from some of their neighboring agents through communication links to keep the distances between them constant.All the available communication links and the communication links being used to maintain the formation shape constitute the network topology and communication topology of the persistent formation respectively.[16]To ensure that the persistent formation can maintain its formation shape, the communication topology must be a persistent graph of the network topology.Meanwhile,different communication links of each agent may have different communication costs,that is,they consume different energy of the agent, and the available energy of each agent is limited, so it is necessary to optimize the communication topology of a persistent formation to minimize the energy consumption of the agents.
With the aim of minimizing the sum of the communication costs of all communication links in the communication topology, also called the formation communication cost, the concept of a min-weighted persistent formation[17]or an optimally persistent formation[18]has been proposed.To generate the communication topology of an optimally persistent formation, a generation algorithm based on optimally rigid graph and triangular configuration has been proposed,[17]which is suitable for a specific two-dimensional(2D)formation shape.Two generation algorithms based on optimally rigid graph and several oriented operations have been proposed,[19,20]which are suitable for any 2D and three-dimensional (3D) formation shape respectively.In addition, a generation algorithm based on optimally rigid graph with a top–down strategy has been proposed,[21]which can be applied to some 3D formation shapes.
Furthermore,considering the leader constraint(only certain agents can act as the leader of the formation), two algorithms called LC-HMAS-OPFGA[16]and CTOA-3DPFLC,[22]based on optimally rigid graph,minimum cost arborescence (MCA), and path reversal operation, have been proposed,which are suitable for any 2D and 3D formation shapes respectively.Then, two corresponding improved algorithms with less calculation time,called FOA-CT-2DPF[23]and FGACT-3DOPF,[24]have also been proposed.
In summary, the existing studies have mainly addressed the offline optimization problem of communication topology for persistent formation without communication faults.However, owing to hostile attacks, signal jamming or occlusion,mechanical or communication hardware failure and so on,a persistent formation may suffer communication faults during formation movement.These communication faults may cause some communication links in the current communication topology to no longer be usable or some agents to withdraw from the formation.[25]As a result,the formation shape cannot be maintained, and agent collisions may even occur in serious cases.Therefore, it is necessary to optimize the communication topology after such communication faults to ensure the safety of all agents and continue to maintain the formation shape while reducing the formation communication cost as much as possible.Therefore,studied in this work is the optimization problem of communication topology for persistent formation in case of communication faults, and the main novel contributions of this paper are as follows.
(i) A two-stage optimization model is proposed, which decomposes this problem into two simpler subproblems, that is, the fast reconstruction subproblem of communication topology and the re-optimization subproblem of communication topology.
(ii) For the first subproblem, a fast reconstruction algorithm of communication topology, based on optimally rigid graph, arc addition operation and path reversal operation, is proposed,which can ensure the safety of the agents in a timely manner and maintain the formation shape.
(iii) For the second subproblem, a re-optimization algorithm of communication topology,based on agent position exchange,is proposed,which can ensure that the formation communication cost is as low as possible while still maintaining the formation shape.
The remainder of this article is organized as follows.The problem analysis and modeling are discussed in Section 2.In Section 3,the proposed algorithms are presented in detail,and their time complexities are analyzed.In Section 4, the effectiveness of the proposed algorithms is validated by numerical experiments.Concluding remarks and expectations are presented in Section 5.
2.Problem analysis and modeling
First, some basic knowledge about persistent formation is presented.Second,the communication fault constraint of a persistent formation is analyzed.On this basis,a two-stage optimization model is proposed to model the optimization problem of communication topology for persistent formation in case of communication faults.
2.1.Basic knowledge about persistent formation
The formation shape, network topology, communication topology, leader constraint, and communication fault constraint of persistent formation are introduced respectively.
2.1.1.Formation shape of persistent formation
Thed-dimensional formation shape of a persistent formation composed ofnagents can be represented by ann×3 matrixS,[23,24]as shown below:
Here, the positions in the formation shape are numbered as 1,2,...,n, and (xi,yi,zi) represent the relative coordinates of thei-th position in a coordinate system.In particular,whendis equal to 2,the value ofzi(1≤i ≤n)is 0.
2.1.2.Network topology of persistent formation
The network topology of a persistent formation includes all of the available communication links between agents, and can be represented by a weighted digraphD=(V,A,W,P)as follows.[23,24]
i)V={vi},1≤i ≤n,is the set of vertices,wherevirepresents thei-th agent.
ii)A={aij}⊂V×V,1≤i/=j ≤n, is the set of arcs,whereai j=(vi,vj)denotes that there is a communication link fromvitovjsuch thatvican send information tovj.
iii)W={wij},aij ∈A, is the set of arc weights, wherewijdenotes the communication cost ofaij,which is equivalent to the communication distance fromvitovj.
iv)P={pi},1≤i ≤n,is the set of specific positions of agents, referred to as the agent position configuration, wherepirepresents the number of the specific position ofviinS.
2.1.3.Communication topology of persistent formation
The communication topology of a persistent formation is a persistent graph in its network topology.It can be expressed asT=(V,A∗,W∗,P),A∗⊆A,W∗⊆W,and has the following attributes.[23,24]
(I)Its underlying undirected graph is a rigid graph.
(II)aij ∈A∗indicates that the communication link fromvitovjis used during the formation movement.
(IV)|A∗| represents the total number of communication links in the communication topology,which must satisfy|A∗|≥d×(|V|−3)+3.When|A∗|=d×(|V|−3)+3, the communication topology is a minimally persistent graph,and the persistent formation is a minimally persistent formation.
(V)w(T)=∑ai j∈A∗wi jrepresents the formation communication cost.If the correspondingw(T) of the current communication topology is the smallest in all possible persistent graphs in the same network topology,then this communication topology is an optimally persistent graph, and this formation is an optimally persistent formation.
2.1.4.Leader constraint of persistent formation
To facilitate agent control,the leader-first-follower(LFF)or leader-remote-follower(LRF)control mode is usually used by a persistent formation to maintain a 2D formation shape.Furthermore, for a heterogeneous persistent formation, only specific agents can act as the leader in the LFF or LRF control mode, and these candidate leaders can be represented byVl ⊆V.Therefore,the leader constraint of a 2D persistent formation can be described as Eq.(2),[23]in whichviacts as the leader.
Similarly,the leader-first follower-second follower(L-FF-SF)control mode is usually used by a persistent formation to maintain a 3D formation shape, and the leader constraint of a 3D persistent formation can be described as follows:[24]
wherevi,vj,andvkact as the leader,the first follower,and the second follower,respectively.
2.2.Communication fault constraint of persistent formation
Four specific types of communication faults can be summarized in Table 1.[26]

Table 1.Four types of communication faults.
Meanwhile, for all agents to be informed of the same communication fault information in time, we assume that all agents have the same diagnosis and identification strategy of communication faults based on a broadcast communication channel(BC)as indicated in the studies of Giuliettiet al.,[27]Polliniet al.,[28]and Yanget al.[29]
In summary,different types of communication faults will make certain communication links invalid or cause certain agents to withdraw from the formation.LetA−={axy},1≤x /=y ≤n, represent the set of invalid communication links, and letV−={az}, 1≤z ≤n, denote the set of agents that must be withdrawn from the formation.If the current communication topology contains one or more of these invalid communication links or if one or more of the agents need to be withdrawn from the formation,then the current communication topology can no longer be used to maintain the formation shape,and the communication topology must be adjusted.Therefore, the communication fault constraint of a persistent formation can be described as follows:
That is, the adjusted communication topology cannot contain any invalid communication links,nor can it contain any agent that needs to withdraw from the formation.
2.3.Problem modeling
When a communication fault prevents the current communication topology from being used to maintain the formation shape, if the communication topology is not adjusted in time, this communication fault may lead to collision accidents between agents.[25]Therefore, after a communication fault occurs,the communication topology must be quickly reconstructed to ensure the safety of the agents and restore the formation shape.After the communication topology reconstruction, the security of the persistent formation is ensured.At this time,the communication topology can be reoptimized via agent position exchange(e.g.,exchanging the positions of two agents in the formation or having one agent filling in the space left by another agent exiting the formation) to achieve the minimal formation communication cost required to continue to maintain the formation shape.Based on the above analysis, the optimization problem of communication topology for persistent formation in case of communication faults can be decomposed into the following two subproblems.
I) Fast reconstruction subproblem of communication topology for persistent formation
First,the corresponding invalid arcs or invalid vertices are removed from the current network topologyD=(V,A,W,P)to obtain a reconstructed network topologyDr=(Vr,Ar,Wr,Pr)that satisfies the communication fault constraint; then, a suitable subgraphTrneeds to be quickly selected fromDras the reconstructed communication topology.
The reconstructed communication topology must be a persistent graph inDr; however, there may be more than one graph like this inDr,of which,the optimally persistent graph has the lowest formation communication cost.Moreover, because only certain agents can serve as the leader, it may not be possible to use any arbitrary optimally persistent graph inDras the reconstructed communication topology.Therefore,this problem is modeled as an optimization problem of obtaining the optimally persistent graph inDrthat satisfies the leader constraint and the communication fault constraint.
II)Re-optimization subproblem of communication topology for persistent formation
Since different position exchanges will result in different agent position configurationsPmand there are multiple feasible communication topologies for eachPm, in this work this problem is modeled as a combinatorial optimization problem in which the leader constraint and the communication fault constraint must be satisfied: the objective is to select an optimal position configurationPofrom the set of all possible agent position configurations{Pm}such that the formation communication cost of the corresponding optimal communication topologyTois globally minimum.
Specifically, the network topologyDmthat satisfies the communication fault constraint is constructed for eachPm,and then,the optimally persistent graphTmthat satisfies the leader constraint inDmis obtained.Finally,the graph with the lowest formation communication cost is selected as the reoptimized communication topologyTofrom among allTm, and the corresponding agent position configurationPois the reoptimized agent position configuration.
The necessary and sufficient conditions for an optimally persistent graph are shown in Lemma 1 as follows.
Lemma 1[16,22]A weighted digraphD=(V,A,W) is ad-dimensional optimally persistent graph if and only if it satisfies the following two conditions:
(i)The in-degree of each vertex is no greater thand.
(ii) The corresponding weighted undirected graph,G=(V,E,W),is ad-dimensional optimally rigid graph.
The necessary and sufficient conditions for an optimally rigid graph, as mentioned in condition 2 of Lemma 1, are shown in Lemma 2 as follows.
Lemma 2[16,22]A weighted undirected graphG=(V,E,W)is ad-dimensional optimally rigid graph if and only if it satisfies the following three conditions:
i)The number of edges,|E|,isd×(|V|−3)+3.
ii)The corresponding rigidity matrix,M ∈R|E|×(3×|V|),is full rank,that is,the rank ofMisd×(|V|−3)+3.
iii)The sum of the weights of all edges inEis the smallest in all weighted undirected graphs that have the same vertices and satisfy conditions 1 and 2.
3.Model-solving algorithms
For solving the above two subproblems, a fast reconstruction algorithm of communication topology for persistent formation (FRA-CT-PF), based on optimally rigid graph, arc addition operation and path reversal operation, is proposed.Then,a re-optimization algorithm of communication topology for persistent formation (ROA-CT-PF), based on agent position exchange, is proposed.The details of these two algorithms are described in the following subsections.
3.1.FRA-CT-PF
The algorithm first deletes invalid arcs and vertexes from current network topology to obtain a reconstructed network topology, then generates an optimally rigid graph of this reconstructed network topology by considering the communication fault constraint,and transforms the optimally rigid graph into an optimally persistent graph satisfying the communication fault constraint through converting into a digraph, obtaining the intersection with current communication topology, arc addition and path reversal operations.Finally, the algorithm makes the optimally persistent graph satisfy both the leader constraint and the communication fault constraint through path reversal operation.The pseudocode of FRA-CTPF is shown in Table 2.
Next, the correctness of FRA-CT-PF is proved theoretically.
Theorem 1The reconstructed communication topologyTrobtained by FRA-CT-PF must be the optimally persistent graph in the reconstructed network topologyDrthat satisfies the leader constraint and the communication fault constraint.
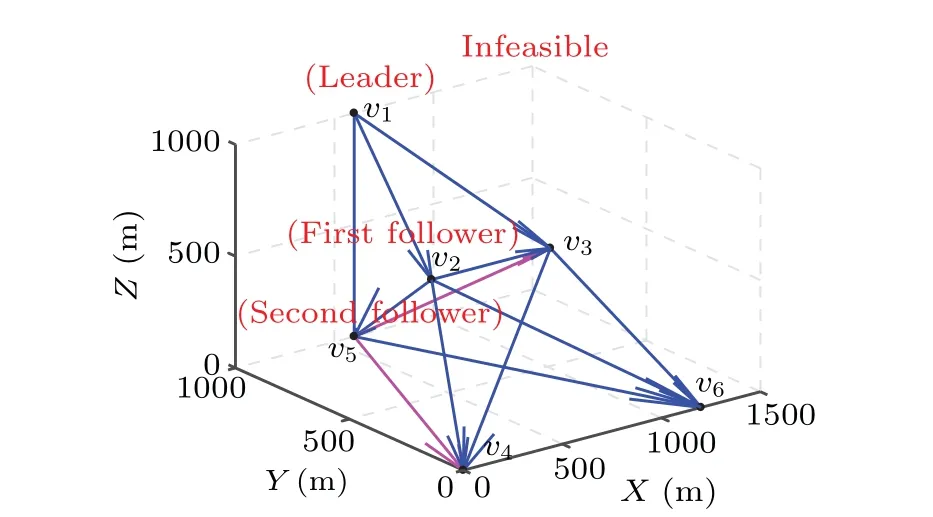
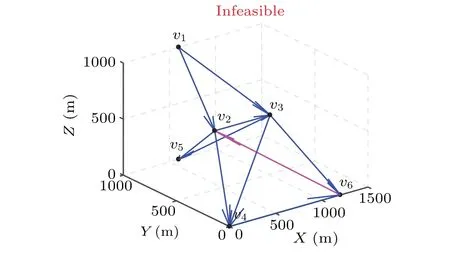
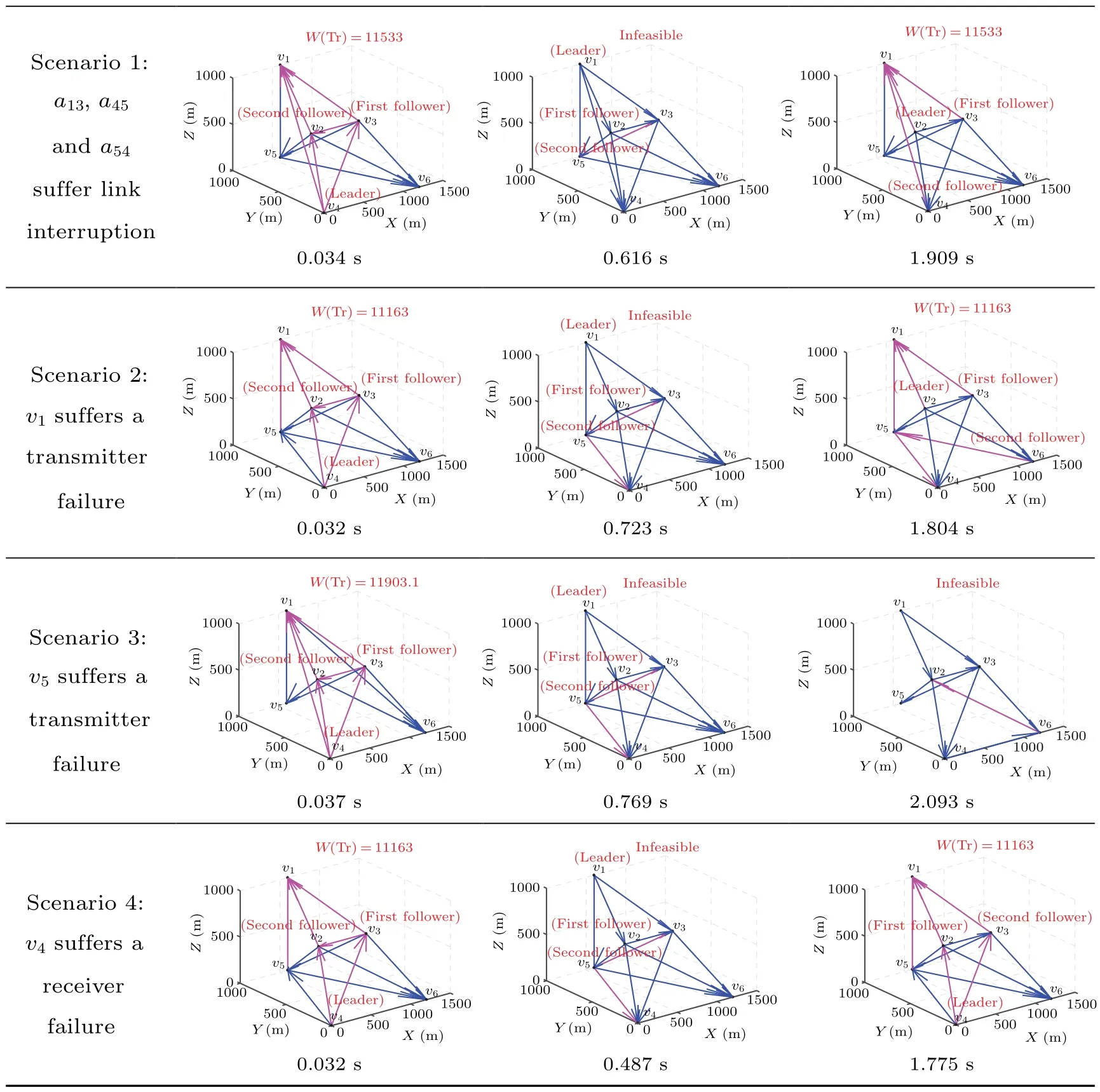
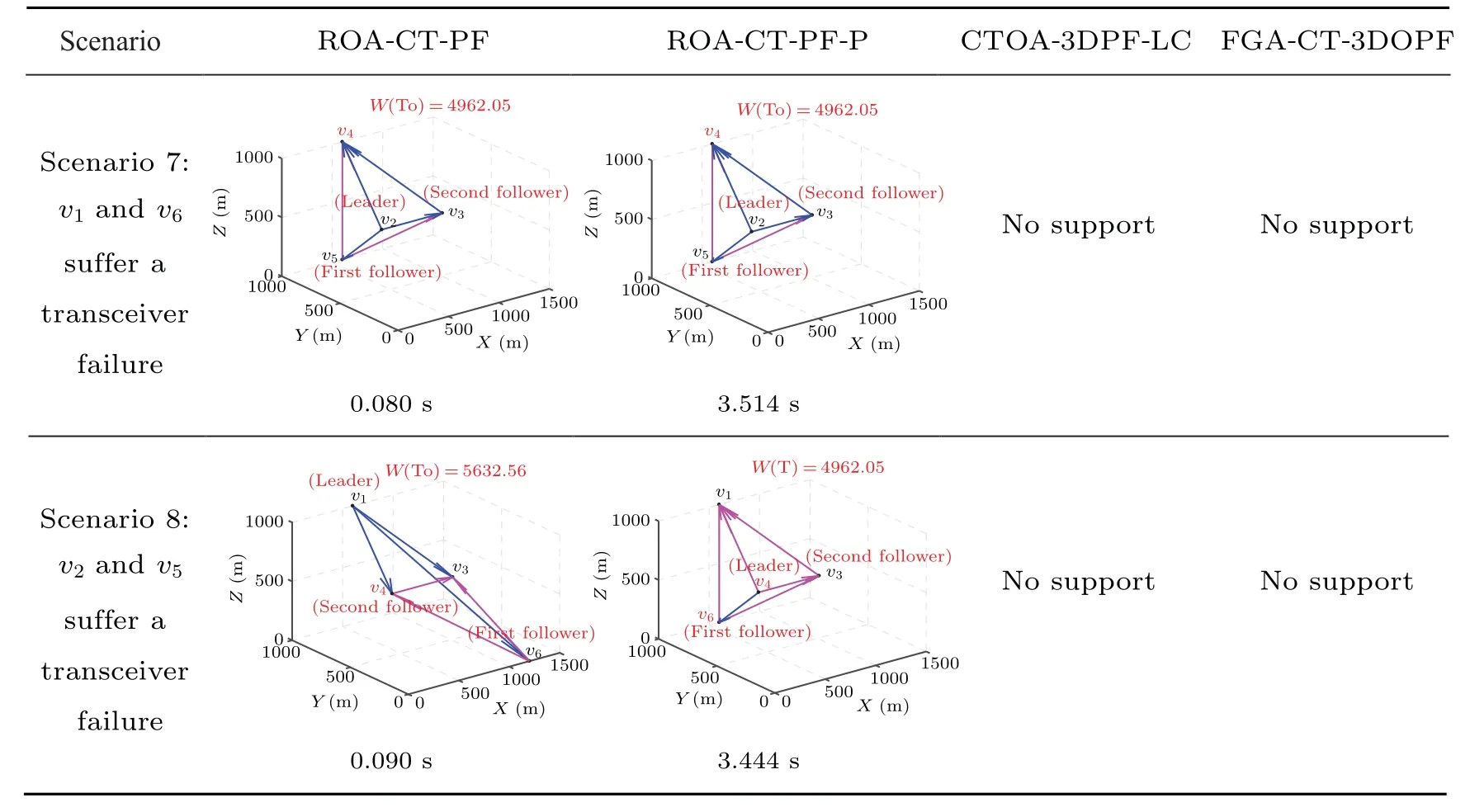
ProofBecauseTis ad-dimensional optimally persistent graph ofD,the in-degree of each vertex inTis no greater thandaccording to Lemma 1.Therefore,after the operation of line 09,the in-degree of each vertex inTris also no greater thand.The premise of the operation of line 15 is(vj) After the operation of line 08,DRris the digraph of optimally rigid graphRr.After the operation of line 09,Tris a subgraph ofDRrand no duplicate arcs exist inTr.In the operations of lines 11 to 27, all arcs added toTrmust belong toDRrand no duplicate arcs are added toTr.Meanwhile, after the operations of lines 11 to 27,m=d×(|Vr|−3)+3.In the operations of lines 28 to 36, only the direction of some arcs inTris changed.Therefore,the corresponding weighted undirected graph of the finalTrmust be the optimally rigid graphRr.That is,Trobtained by FRA-CT-PF must satisfy condition 2 of Lemma 1. Because all conditions of Lemma 1 are satisfied,Trobtained by FRA-CT-PF must be ad-dimensional optimally persistent graph inDr. After the operation of lines 28 to 36,d=2 and equation (2) are satisfied, ord=3 and equation (3) are satisfied.Therefore,Trobtained by FRA-CT-PF must satisfy the leader constraint. After the operation of line 03,A−andV−are deleted fromDr,which means thatDrsatisfies the communication fault constraint.After the operations of lines 08 to 09,DRris the subgraph ofDrandTris the subgraph ofDRr, soTrsatisfies the communication fault constraint.In the operations of lines 11 to 36,all arcs added toTrmust belong toDRrand all the reverse paths must exist inDRr.Therefore,Trobtained by FRA-CT-PF must satisfy the communication fault constraint. In summary,Trobtained by FRA-CT-PF must be the optimally persistent graph inDrthat satisfies the leader constraint and the communication fault constraint. The time complexity of FRA-CT-PF is analyzed as follows.In this algorithm,the main calculation time is in lines 07,19,22,31,33,and 34,respectively.Line 07 is an improvement on the original optimally rigid graph generation algorithm,[30]and its time complexity is approximatelyO(|Vr|4).Lines 19,22, 31, 33, and 34 use the classical Dijkstra shortest path algorithm, and the time complexity of each of them is approximatelyO(||+|Vr|×log|Vr|).Because|Vr|≤|V| and||≤|Ar|≤|V|×(|V|−1),the total time complexity of FRACT-PF is aboutO(|Vr|4+4×(||+|Vr|×log|Vr|))≈O(|V|4). To obtain a reoptimized communication topology through agent position exchange,the following solution method can be adopted.First, for each agent position configurationPm, the network topologyDmthat satisfies the communication fault constraint is constructed.Then,the optimally persistent graphTmthat satisfies the leader constraint and the communication fault constraint in eachDm, is obtained.Finally, the graph with the lowest formation communication cost is selected from among allTmas the reoptimized communication topology,To. However, eachPmmust be a permutation of the selection of|Vr| positions from among the|V| positions in the formation shape, so the total number of all possiblePmis|V|!/(|V|−|Vr|)!.As the value of|V| continues to increase,the corresponding value of|V|!/(|V|−|Vr|)! becomes very large,indicating that it is difficult to obtain a solution in a limited time.Therefore, ROA-CT-PF is proposed in this work to achieve a suboptimal reoptimized communication topology through position exchange between only two agents.Nevertheless, it can still obtain a good reoptimized communication topology, as verified in the following numerical experiments.The pseudocode of this algorithm is shown in Table 3. Table 3.Pseudocode of ROA-CT-PF. Next, the correctness of ROA-CT-PF is proved theoretically. Theorem 2The reoptimized communication topologyToobtained by ROA-CT-PF must be feasible and its formation communication cost is no more than that ofTrobtained by FRA-CT-PF. ProofIn the operation of line 01,Tois initialized by the reconstructed communication topologyTrobtained by FRACT-PF.According to Theorem 1,Trmust be feasible, so the initialTois feasible.In the operation of line 08, FRA-CT-PF is used to obtain the corresponding optimal reconstructed communication topologyTm.According to Theorem 1,Tmmust be feasible.In the operations of lines 10 and 12,Tois replaced byTm.Therefore,Toobtained by ROA-CT-PF must be feasible. In the operation of line 01,Tois initialized by the reconstructed communication topologyTrobtained by FRA-CT-PF,so the formation communication cost of the initialTois equal to that ofTr.In the operations of lines 09 to 13, only whenw(Tm)≤w(To)Tocan be replaced byTm.Therefore,the formation communication cost ofToobtained by ROA-CT-PF is no more than that ofTrobtained by FRA-CT-PF. The time complexity of ROA-CT-PF is analyzed as follows.Line 08 is the core step of this algorithm and is the same as lines 06 to 36 of FRA-CT-PF;therefore,the time complexity of line 08 is approximatelyO(|V|4).In line 06 the number of possible combinations of two positions selected from among the|V|total positions is|V|×(|V|−1)/2; that is, the total number of all feasiblePmis|V|×(|V|−1)/2.Therefore,it can be seen from line 05 of this algorithm that line 08 will run|V|×(|V|−1)/2 times at most.Consequently, because|Vr|≤|V|, the time complexity of this algorithm is approximatelyO(|V|4×|V|×(|V|−1)/2)≈O(|V|6). Next, several numerical experiments are carried out to verify the effectiveness of the proposed algorithms. Assuming that there are no communication faults at the beginning,all agents are able to communicate with each other,viis located at thei-th position inSand onlyv1,v2,andv4can serve as leaders,so the initial network topology is shown in Fig.2(a)and its corresponding Laplace matrix is The initial communication topology of this persistent formation,obtained by CTOA-PF-LC,[22]is shown in Fig.2(b).Its corresponding Laplace matrix is Fig.2.Initial network topology and communication topology of this persistent formation,showing(a)initial network topology and(b)initial communication topology. In this communication topology,v1,v2, andv5are the leader, the first follower, and the second follower, respectively,and the formation communication cost is 11163,whileP={1,2,3,4,5}is the corresponding agent position configuration.To easily distinguish the in-degree of each vertex in figures,arcs from small-to large-numbered vertices are drawn with blue solid lines, and other arcs are drawn with magenta solid lines. To verify the effectiveness of proposed algorithms under various types of communication faults in Table 1, eight communication fault scenarios as shown in Table 4, are designed and the corresponding numerical experiments are carried out.Among these scenarios,because the influence of a transmitter or transceiver failure on a leader in the communication topology is very different from that of a transmitter or transceiver failure on a non-leader,scenarios 2 and 3 are designed to represent transmitter failures on a leader and a non-leader, and scenarios 5 and 6 are designed to represent transceiver failures on a leader and a non-leader, respectively.In addition, scenarios 7 and 8 are designed to represent transceiver failures on two agents. The development environment of all algorithms is Visual Studio 2013, and the programming language is C++.All experiments are performed on a computer with an 8-core i7 4.0-GHz processor,16-GB RAM and a Windows 10 operating system. First, scenario 3 is used to illustrate the calculation process of FRA-CT-PF.It is assumed thatv5suffers a transmitter failure based on the current network topology shown in Fig.2(a) and the current communication topology shown in Fig.2(b).At the same time, onlyv1,v2, andv4can serve as leaders.Namely,the communication fault constraint is denoted byA−={a5y},1≤y ≤6 andV−= /0, and the leader constraint is represented byVl={v1,v2,v4}.Then,the main calculation process of this algorithm is as follows. In line 02, the invalid arcs and vertexes are deleted from current network topology,and the reconstructed network topologyDris shown in Fig.3(a).Its corresponding Laplace matrix is In line 07,the optimally rigid graphRrofGris generated as shown in Fig.3(b),which satisfies that the degree of each vertex inRris no more than the number of bidirectional arcs of this vertex inGrplus 3.This additional condition ensures thatRrcan be directed to an optimally persistent graph satisfying the communication fault constraint. In line 08,Rris converted into a digraphDRrsatisfying the communication fault constraint,and it is shown in Fig.3(c).Its corresponding Laplace matrix is In line 09,the intersection ofDRrandTis obtained and used to reinitializeTr,as shown in Fig.3(d). Fig.3.Calculation process of FRA-CT-PF under scenario 3,showing(a)constructed network topology,(b)optimally rigid graph Rr,(c)digraph corresponding to Rr,(d)intersection Tr of DRr and T,(e)Tr after adding a14,(f)Tr after adding a15,(g)Tr after adding a16,(h)Tr after adding a25,(i)Tr after reversing(1,4),(j)Tr after reversing(6,3),(k)Tr after reversing(6,2),and(l)reconstructed communication topology. In line 10,the number of its arcs,m,is 8. In line 11,becausem<3×|Vr|−6,the operations in lines 12 to 26 will be performed untilm=3×|Vr|−6.The specific process is as follows: whenl=1,thel-th edgeei jinRrise14,neithera14nora41exists inTr,d(v4)=0<3 anda14∈DRr,soa14is added toTrin line 15 as shown in Fig.3(e).Similarly, whenl=2,a15is added toTras shown in Fig.3(f).Whenl=3,a16is added toTras shown in Fig.3(g).Whenl=4,a25is added toTras shown in Fig.3(h). In line 28, because the leader constraint is not satisfied,jumps directly to line 31. In line 31,v4is found to be the leader because it satisfiesv4∈Vl.However, becaused(v4)=1 now, a path (1,4) is found inTrand its arcs are reversed inTras shown in Fig.3(i),where the reversed path is identified by dashed lines.After this path reverse operation,Trsatisfiesd(v4)=0 andTr⊆DRr.Therefore,v4acts as the leader. In line 33,v3is found because it satisfiesa43∈.However,becausedr(v3)=2 now,a path(6,3)is found inTrand its arcs are reversed inTras shown in Fig.3(j), where the reversed path is identified by dashed lines.After this path reverse operation,Trsatisfiesa43∈,d(v3)=1 andTr⊆DRr.Therefore,v3acts as the first follower. In line 34,v2is found because it satisfiesa42,a32∈.However, because(v2)=3 now, a path (6,2) is found inTrand its arcs are reversed inTras shown in Fig.3(k),where the reversed path is identified by dashed lines.After this path reverse operation,Trsatisfiesa42,a32∈,(v2)=2 andTr⊆DRr.Therefore,v2acts as the second follower. In line 37,Tris the reconstructed communication topology as shown in Fig.3(l), and the corresponding formation communication cost is 11903.1.Its corresponding Laplace matrix is Comparatively,if CTOA-3DPF-LC[22]is used to acquire the reconstructed communication topology in this case,the finalTrobtained is shown in Fig.4.However, the arcsa53,a54, anda56exist in the finalTr, which means that the finalTrdoes not satisfy the communication fault constraint.Therefore, the reconstructed communication topology obtained by CTOA-3DPF-LC is infeasible. Fig.4.Reconstructed communication topology obtained by CTOA-3DPF-LC. Similarly,if FGA-CT-3DOPF[24]is used to obtain the reconstructed communication topology in this case, the finalTrobtained is shown in Fig.5.However, it does not satisfy the condition 1 of Lemma 2.Therefore, the reconstructed communication topology obtained by FGA-CT-3DOPF is also infeasible. Fig.5.Reconstructed communication topology obtained by FGA-CT-3DOPF. Table 5.Reconstructed communication topologies and calculation time under eight scenarios. Scenario FRA-CT-PF CTOA-3DPF-LC FGA-CT-3DOPF Table 5.(Continued). Next, for the eight communication fault scenarios in Table 4, the reconstructed communication topologies obtained by FRA-CT-PF and existing algorithms, and the calculation time of these algorithms are shown in Table 5. In scenario 1, the reconstructed communication topologies obtained by FRA-CT-PF and FGA-CT-3DOPF are both feasible and have the same formation communication cost.However,the reconstructed communication topology obtained by CTOA-3DPF-LC is infeasible because it does not satisfy the communication fault constraint.In scenarios 2 and 4, the same conclusion can be drawn. In scenario 3, the reconstructed communication topology obtained by FRA-CT-PF is feasible.However,the reconstructed communication topology obtained by CTOA-3DPFLC is infeasible because it does not satisfy the communication fault constraint.Meanwhile,the reconstructed communication topology obtained by FGA-CT-3DOPF is infeasible because it does not satisfy the condition 1 of Lemma 2. In scenario 5, the reconstructed communication topologies obtained by FRA-CT-PF,CTOA-3DPF-LC and FGA-CT-3DOPF are both feasible and have the same formation communication cost.In scenarios 6,7,and 8,the same conclusion can be drawn. Meanwhile,in all scenarios,the average calculation time of FRA-CT-PF is only 3.48%of that of CTOA-3DPF-LC,but only 1.02%of that of FGA-CT-3DOPF. In summary, compared with existing algorithms, FRACT-PF proposed in this paper can always obtain feasible reconstructed communication topology in all communication fault scenarios,and its calculation time is much less. First,scenario 3 continues to be used to illustrate the calculation process of ROA-CT-PF.Based on the reconstructed communication topology as shown in Fig.3(l),the calculation process of ROA-CT-PF is as follows. In line 01,Tois equal toTrandPois equal toPr. In line 02,becausew(To)=11903.1 andw(T)=11163,the algorithm executes the operations of lines 05 to 14. Whenm= 2, the correspondingP2in line 06 is{2,1,3,4,5,6}and the correspondingT2in line 08 is shown in Fig.6(a),wherev1andv2exchange their positions in the formation shape andw(T2)=11903.1.Becausew(T2)=w(To)and the total agent movement distance for switching fromPrtoP2is 1562.05, which is more than that fromPrtoPo, there is no change inTonorPo. Whenm= 3,P3is{3,2,1,4,5,6}andT3is shown in Fig.6(b),wherev1andv3exchange their positions in the formation shape andw(T3)=11903.1.Becausew(T3)=w(To)and the total agent movement distance for switching fromPrtoP3is equal to that fromPrtoPo,there is no change inToandPo,either. Whenm= 4,P4is{4,2,3,1,5,6}andT4is shown in Fig.6(c),wherev1andv4exchange their positions in the formation shape andw(T4)=11903.1.Becausew(T4)=w(To)and the total agent movement distance for switching fromPrtoP4is 3072.46, which is more than that fromPrtoPo, there is also no change inTonorPo. Whenm= 5,P5is{5,2,3,4,1,6}andT5is shown in Fig.6(d),wherev1andv5exchange their positions in the formation shape andw(T5)=11163.Becausew(T5) Fromm=6 to the end,the conditions in line 09 or line 11 are not satisfied, so there is no change inTonorPo.Namely,T5is the reoptimized communication topology, wherev1andv5exchange their positions. Fig.6.Example of calculation process of ROA-CT-PF, showing: (a) reconstructed communication topology when m=2, (b) reconstructed communication topology when m=3,(c)reconstructed communication topology when m=4,and(d)reoptimized communication topology. In contrast, lines 05 and 06 of ROA-CT-PF are modified into“whilem<|V|!/(|V|−|Vr|)!do”and“Letm=m+1,and obtain the next permutationPmof the selection of|Vr|positions from among the|V|positions in the formation shape”,and this modified algorithm is called ROA-CT-PF-P.Then, ROA-CTPF-P is used to obtain the reoptimized communication topology in this case.TheToobtained by ROA-CT-PF-P is the same as that obtained by ROA-CT-PF, but the calculation time of ROA-CT-PF-P is much longer than that of ROA-CT-PF. Next, for the eight communication fault scenarios in Table 4,the reoptimized communication topologies obtained by FRA-CT-PF and existing algorithms,and the calculation time of these algorithms are shown in Table 6. In scenario 1,because the formation communication cost of reconstructed communication topology is more than that of current communication topology, the operations of agent position exchange in ROA-CT-PF and ROA-CT-PF-P will be executed.The reoptimized communication topologies obtained by ROA-CT-PF and ROA-CT-PF-P are the same.However,the calculation time of ROA-CT-PF is much less than that of ROA-CT-PF-P.Meanwhile, both CTOA-3DPF-LC and FGACT-3DOPF do not support the re-optimization of communication topology for persistent formation.In scenarios 3,5,6,and 7,the same conclusion can be drawn. In scenario 2,because the formation communication cost of reconstructed communication topology is equal to that of current communication topology, the operations of agent position exchange in ROA-CT-PF and ROA-CT-PF-P will not be executed.That is,the reoptimized communication topologies obtained by ROA-CT-PF and ROA-CT-PF-P are the same as the reconstructed communication topology, and the calculation time of ROA-CT-PF and ROA-CT-PF-P are both approximately equal to 0.In scenario 4,the same conclusion can be drawn. Table 6.Reoptimized communication topologies and calculation time under eight scenarios Table 6.(Continued). In scenario 8,because the formation communication cost of reconstructed communication topology is more than that of current communication topology, the operations of agent position exchange in ROA-CT-PF and ROA-CT-PF-P will be executed.The formation communication cost of the reoptimized communication topology obtained by ROA-CT-PF is more than that by ROA-CT-PF-P.This shows that ROA-CTPF cannot ensure obtaining the optimal reoptimized communication topology through position exchange between only two agents.However,the calculation time of ROA-CT-PF is much less than that of ROA-CT-PF-P. In summary,the following conclusions can be drawn from Table 6: (i) Compared with CTOA-3DPF-LC and FGA-CT-3DOPF,the ROA-CT-PF proposed in this paper can reoptimize the communication topology to further reduce the formation communication cost based on the reconstructed communication topology. (ii)Compared with ROA-CT-PF-P,the ROA-CT-PF proposed in this paper can almost obtain the same reoptimized communication topology in all communication fault scenarios,and the calculation time is much less. In this paper, the optimization problem of communication topology for persistent formation in case of communication faults is studied.This problem is decomposed into two subproblems, namely, the fast reconstruction subproblem of communication topology and the re-optimization subproblem of communication topology. To address the fast reconstruction subproblem of communication topology, an algorithm called FRA-CT-PF, based on optimally rigid graph,arc addition operation and path reversal operation, is proposed.Compared with existing algorithms,the algorithm can always obtain feasible reconstructed communication topology in all communication fault scenarios,and its calculation time is much less. To address the re-optimization subproblem of communication topology, an algorithm called ROA-CT-PF, based on agent position exchange,is proposed.Compared with existing algorithms,the algorithm can obtain a reoptimized communication topology to further reduce the formation communication cost in a shorter time. In the future,a distributed optimization algorithm of communication topology for persistent formation in case of communication faults will be studied. Acknowledgements Project supported by the National Natural Science Foundation of China(Grant Nos.71871079,72271076,71971075,and 71671059) and the Anhui Provincial Natural Science Foundation,China(Grant No.1808085MG213).3.2.ROA-CT-PF

4.Numerical experiments
4.1.Experimental settings

4.2.Experimental results of fast reconstruction of communication topology

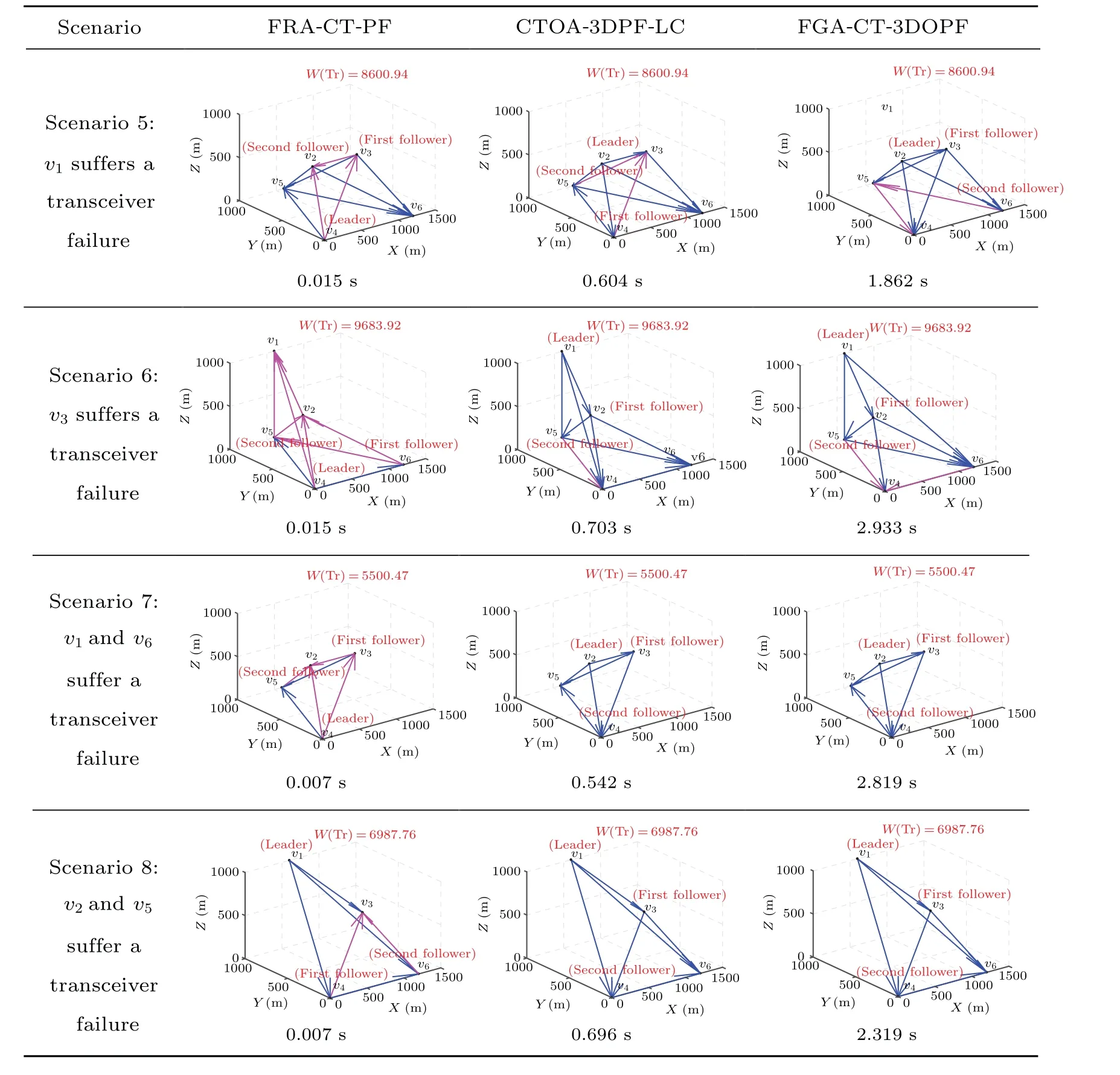
4.3.Experimental results of re-optimization of communication topology


5.Conclusion and perspectives
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- First-principles calculations of high pressure and temperature properties of Fe7C3
- Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station
- Energy conversion materials for the space solar power station
- Stability of connected and automated vehicles platoon considering communications failures
- Lightweight and highly robust memristor-based hybrid neural networks for electroencephalogram signal processing
- Method of simulating hybrid STT-MTJ/CMOS circuits based on MATLAB/Simulink
