Monte Carlo calculation of the exposure of Chinese female astronauts to earth’s trapped radiation on board the Chinese Space Station

Yipan Guo(郭义盼), Fazhi Yan(闫发智), Meihua Fang(方美华),†,Zhao Zhang(张昭), Wei Cheng(成巍), and Bing Guo(郭兵)

1Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

2Beijing Institute of Applied Meteorology,Beijing 100029,China

Keywords: space radiation,Chinese female voxel phantom,China’s Space Station,radiation exposure risk

1.Introduction

China has been constructing its space station since April 2021.Despite the protection provided by the Earth’s atmosphere, astronauts on board the Chinese Space Station (CSS)are still exposed to space radiation, which is the main health risk during spaceflight.

Missions in different orbits face different levels of radiation exposure.Astronauts on board the CSS are exposed to two primary types of radiation: galactic cosmic rays(GCRs)and trapped radiation(TR).Experiments and simulations have been conducted to explore the space radiation hazards that astronauts are exposed to.Experiments have been performed to measure the radiation doses received by humanlike phantoms including a phantom head (1989–1990),[1]a spherical phantom (1979–1999),[2]the phantom torso ‘Fred’(1998, 2001),[3–5]and the MATROSHKA series of mannequins(MATROSHKA-R 2004-2005,[6–8]MATROSHKA-1 2004-2005,[9]MATROSHKA-2A 2005,[10]MATROSHKA-2B 2007,[10]and MATROSHKA-KIBO 2010-2011[11]) on board spacecraft.These human-like phantoms were well instrumented with radiation detectors in their vital organs so as to measure the biological radiation parameters, including the dose, the equivalent dose, the effective dose, etc.Computerized anatomical phantoms were also used to calculate the risk posed to astronauts by space radiation.NASA has modeled the computerized anatomical man(CAM),the computerized anatomical female (CAF), the male adult voxel (MAX),and the female adult voxel (FAX) for space radiation hazard analyses.[12]

The above human phantoms were constructed based on European human characteristics.In China, space bio-effect experiments were successfully conducted on board the SJ-1,SJ-4, and SJ-10[13]spacecraft and many space experiments will be scheduled for the CSS.[14]It is essential to construct Chinese human phantoms for space radiation dosimetry simulations.

It is known that long-term radiation sensitivity in females is higher than in males.[15]The dose absorbed by the human body on board the CSS in low Earth orbit(LEO)is mainly due to trapped electrons and protons.[16]In the SZ5,SZ6,and SZ7 missions, the equivalent radiation dose rates contributed by trapped radiation amounted to more than 85%in total.[17]As the orbits of the CSS and those of the SZ5/6/7 missions are relatively similar,trapped radiation is considered to be the main radiation threat to the CSS astronauts.In contrast to GCR particles,trapped radiation is produced by a high flux of electrons and protons.According to the theories describing the interaction between charged particles and the target materials, the energy deposition and shielding strategy for astronauts should take into account the trapped radiation’s characteristics.

This paper describes a Chinese female voxel phantom which was modeled and then implemented using Monte Carlo simulation software to analyze the trapped radiation exposure on board the CSS.The space radiation exposure limits are also discussed.

2.Materials and methods

2.1.Chinese female voxel phantom

The voxel phantom designated to simulate the Chinese female astronaut was incorporated into an Monte Carlo NParticle (MCNP) simulation in order to perform a space radiation risk assessment.The original anatomical data of a female was obtained from Anatonium TM 3D P1 V5.0(www.anatomium.com); it included almost all the organs,skeleton,blood vessels,and lymph present in the human body.The phantom is modeled standing up straight to avoid problems caused by lying down, such as flattening of the female breast.The Rhino 3D software is used to further adjust the original model to the average anatomical characteristics of Chinese women.The physiological parameters of Chinese reference people were obtained from the reference values given in GBZ/T 200-2007,including height,weight,and critical organ mass.[18]The organ volume and density were matched to the values given in Report 46 produced by the International Commission on Radiation Units&Measurements(ICRU)and Publication 89 of the International Commission on Radiological Protection(ICRP).[19]As a result,a Chinese female phantom with a height of 158 cm and a weight of 54 kg was modeled,as shown in Fig.1.

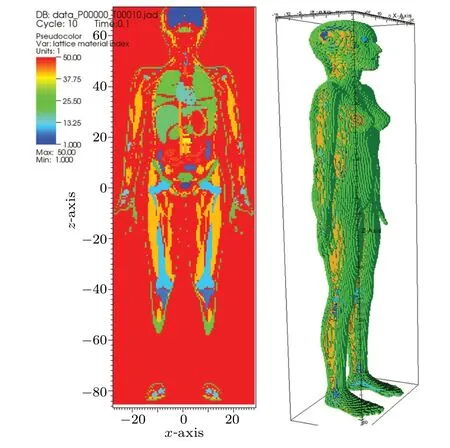
Fig.1.Chinese female astronaut model.

After adjustment,the phantom was re-meshed and transformed into a voxel model for the Monte Carlo dose calculation.[20]The resulting voxel phantom file consisted of 300 slices.Each slice consisted of an array of 7×59 voxels.Each voxel had a size of 5×5×5 mm3,so the total number of voxels in the phantom was more than 1 890 000.A total of 49 organs and tissues can be identified in the voxel phantom.Table 1 lists the organ masses and volumes of the Chinese reference parameters.

Table 1.The final volumes of the organs and tissues of the Chinese female phantom.

2.2.The core module and the equivalent shielding model

The CSS includes three modules: the core module, laboratory module I, and laboratory module II,[21]as shown in Fig.2.The core module,named Tianhe,which has a diameter of 2.2 m and a height of 2.8 m,provides life support and living quarters for the astronauts.In the simulation, aluminum was considered to be an equivalent shielding material.

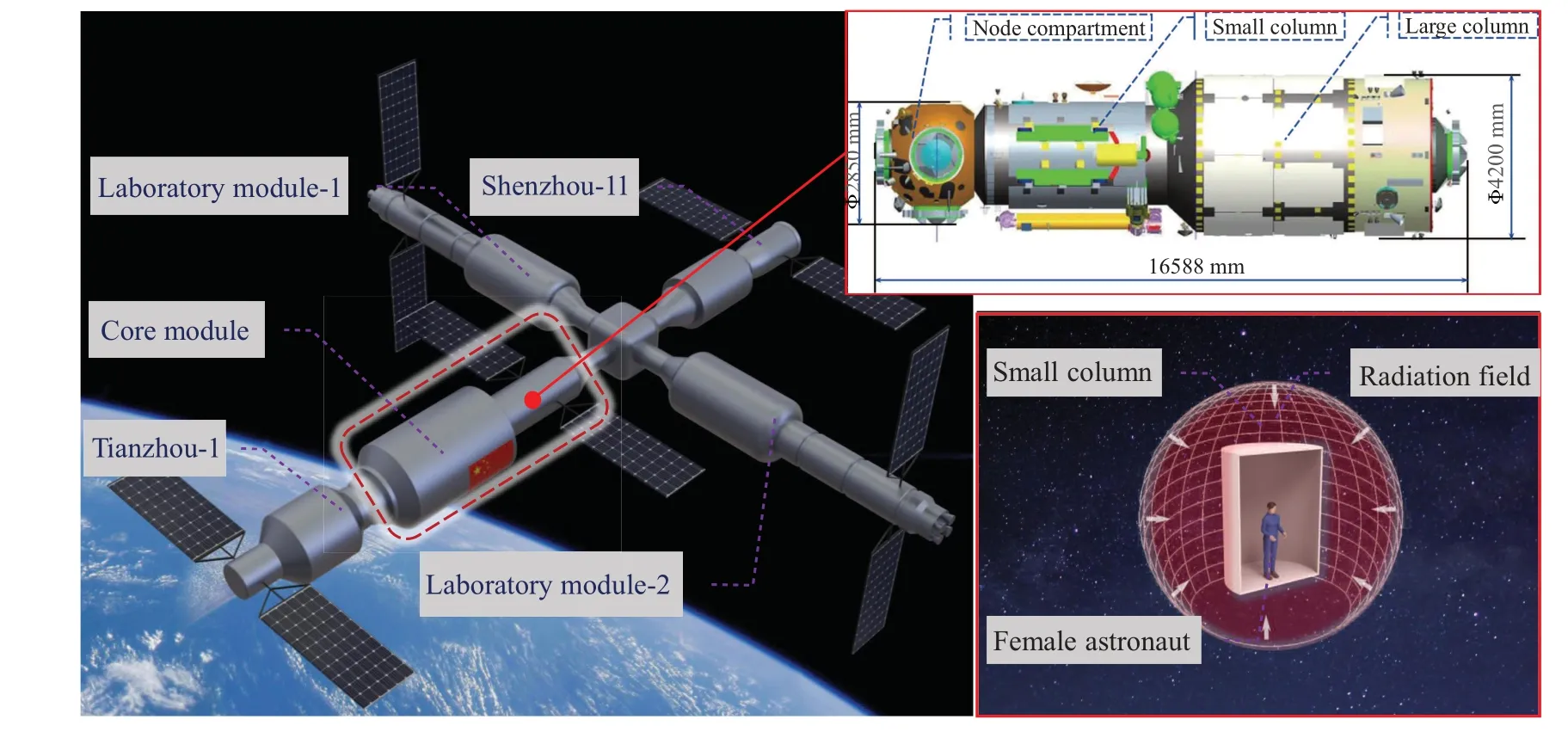
Fig.2.Conceptual model of the Chinese Space Station.

The Tianhe core module was used in the simulation.In the simulation, the core module was simplified to a cylinder with a diameter of 2.2 m and a height of 2.8 m and its material was considered to be equivalent to aluminum.The equivalent shielding thicknesses of aluminum used were 0 g/cm2,1 g/cm2,2 g/cm2,5 g/cm2,10 g/cm2and 20 g/cm2.The spacesuit thickness was considered to be equivalent to 1 g/cm2,the spacecraft shielding thickness was considered to be equal to 2–5 g/cm2, and the shielding thickness for solar particle events was considered to be equal to 10×20 g/cm2.

2.3.Radiation environment

The CSS travels on an orbit with 42◦of inclination and an altitude of 340–450 km.The trapped radiation includes electrons and protons, which play a key role in the radiation exposure risk of astronauts.[22]The energy spectrums of the trapped protons and electrons can be calculated using the AP8 and AE8 models, as shown in Fig.3.The maximum energies of the protons and electrons are 400 MeV and 7 MeV,respectively.In this orbit, the trapped radiation flux exhibits a solar cycle variation.For protons, high fluxes are observed during solar minima and low fluxes are observed during solar maxima.The electron flux varies asynchronously with the solar cycle; specifically, high fluxes are observed during solar maxima and low fluxes are observed during solar minima.The integral flux of protons is two orders of magnitude higher than that of electrons during solar minima and four orders of magnitude higher than that of electrons during solar maxima.

Fig.3.Trapped proton and electron flux: (a)trapped proton spectrum for the solar maximum and minimum;(b)trapped electron spectrum for the solar maximum and minimum.

2.4.Simulation method

Monte Carlo simulations are frequently used to simulate energetic particles’ interactions with matter.[23]In this study,the Monte Carlo software MCNP6 was adopted.MCNP6 is designed to track many particle types:not only N particles,but also charged particles including electrons,protons,and heavy ions over broad energy ranges.[24]In the ray-tracing method,the physical interactions between particles and the atoms of the target material are listed in a table.The energy (∆Ei) deposited in each voxel (i) of the digital model of the human body was recorded using

HereSjis the mass stopping power of the particle; assuming that the mass length of the particle passing through the voxel is ∆d, we divide it intonparts (n=100 in this calculation),∆x=∆d/n.On this basis, the dose absorbed by each voxel can be expressed as follows:

wheremiis the mass of voxeli.The dose equivalentHiof the voxel can now be calculated as follows:

whereQiis the radiation quality factor of the particles incident on voxeli.

The absorbed dose and the dose equivalent given to the organ or tissueTare respectively obtained by summing the absorbed dose and the dose equivalent of all the voxels that make up the organ

wherekis the number of voxels that make up the organT.

The equivalent doseHTgiven to an organ or tissue is calculated as follows:

whereDT,Ris the mean absorbed dose from radiationRin a tissue or organT,andwRis the radiation weighting factor.

The effective doseEcan be calculated according to the equation

whereWTare the tissue weighting factors andHTis the equivalent dose given to an organ or tissueT.The recommendations for the tissue weighting factors are listed in Table 2.[25]

Table 2.Tissue weighting factors from ICRP publication 103.

3.Results and discussion

3.1.Total absorbed dose

The dosesDTabsorbed by the female phantom for different equivalent shielding thicknesses of aluminum during the solar maximum and the solar minimum are shown in Fig.4.The absorbed dose decreases monotonically with increasing shielding thickness.The dose value during the solar minimum is larger than that at the solar maximum, and both doses decrease dramatically for thinner shielding layers.With 1 g/cm2of shielding, the values decrease to 27% and 61% of the total doses during the solar maximum and the solar minimum,respectively.A thickness of 1 g/cm2of aluminum serves as a proxy for the shielding provided by a spacesuit.Therefore, spacesuits contribute significantly to protecting astronauts from radiation hazards.With 10–20 g/cm2shielding,more than 70%of the dose can effectively be removed at both extremes of the solar conditions.

Fig.4.The dose absorbed by a human phantom and the shielding effectiveness in terms of the equivalent aluminum shielding thickness at the solar maximum and the solar minimum: (a) total absorbed dose rate;(b)shielding effectiveness.

This paper usesfas a measure of the shielding effectiveness,which is given by the following formula:

in whichDTis the dose absorbed by the tissue or organTshielded by a thickness ofx.Figure 4(b)represents the shielding effectiveness as a function of the shielding thickness.Apparently,the shielding effectiveness decreases rapidly with increasing shielding thickness,and its value is larger during the solar minimum than during the solar maximum for shielding thicknesses of more than 1 g/cm2.This is the case because most of the dose that passes through the thin layer of shielding is due to trapped electrons and can be easily stopped by material atoms(as detailed in the next section).The shielding effectiveness changes only slightly for more than 5 g/cm2of shielding.

3.2.Critical organ doses

The dependence of the critical organ dose on shielding thickness in the human phantom during the solar maximum and the solar minimum is shown in Fig.5.Among the 49 organs simulated, ten critical organs, including the skin, eyes,brain,heart,ovaries,uterus,stomach,lungs,liver,and breasts,were considered in detail.The shallow organ dose rates are significantly higher than internal organ dose rates,as the shallow organs are susceptible to absorption in the low-energy portions of the electron and proton spectra.Among these ten organs, the skin receives the highest dose and the ovaries receive the lowest dose.The organ dose ratio at the solar maximum is larger than at the solar minimum without shielding,while after shielding, the results are reversed.For example,the skin dose rate reaches 11.9 mGy/d at the solar maximum and 8.29 mGy/d at the solar minimum without shielding,while with 20 g/cm2of shielding, the values are 0.08 mGy/d and 0.34 mGy/d,respectively.

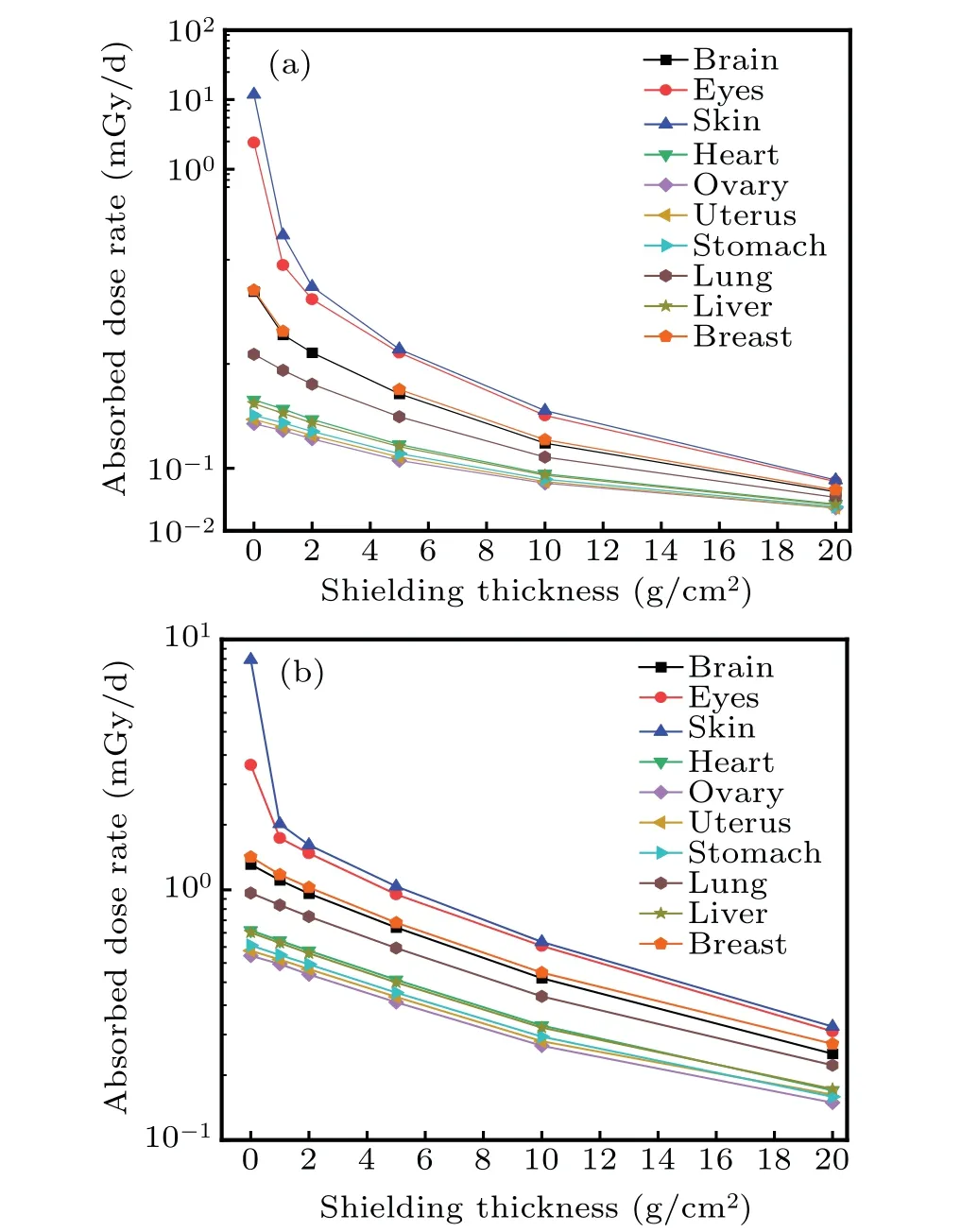
Fig.5.Organs absorbed dose rates for the trapped radiation environment with different equivalent shielding thicknesses of aluminum:(a)at the solar maximum and(b)the solar minimum.

Fig.6.Trapped proton and electron-induced dose rates in organs with different shielding thicknesses at the solar maximum and the solar minimum:(a)trapped proton spectrum at the solar maximum; (b)trapped proton spectrum at the solar minimum; (c)trapped electron spectrum at the solar maximum;(d)trapped electron spectrum at the solar minimum.

The critical organ doses given by different trapped particles after shielding are shown in Fig.6.These results illustrate that the dose depends on the solar conditions, the shielding thickness, the radiation source, and the organ location inside the human phantom.From Figs.6(a)–6(d), one can see that the dose rate of trapped protons absorbed by organs during the solar minimum is about five times higher than the dose received during the solar maximum.Conversely, the absorbed dose rate caused by trapped electrons during the solar minimum is smaller than that caused at the solar maximum.This result can be deduced from the relationship between solar conditions and the trapped electron and proton flux, as shown in Subsection 2.3.Theoretically, 5 g/cm2of shielding can stop electrons and protons with energies of less than 8.5 MeV and 67.5 MeV,respectively,as listed in Table 3,which means that almost all of the trapped electrons can be shielded.Without shielding, the dose rate induced by trapped electrons in the shallow organs is greater than that induced by trapped protons, while with a thin layer of shielding, the organ dose is mainly due to trapped protons.In addition, the internal organ dose rates produced by trapped electrons can be neglected compared to those produced by trapped protons.The shallow organs received larger dose rates at the solar maximum than at the solar minimum,while the internal organs or organs protected by a certain thickness of shielding show the opposite result.The internal organ dose rates are mainly due to trapped protons at both the solar maximum and the solar minimum.The trapped electron-induced organ doses received by the stomach,heart,uterus,and ovaries with 1 g/cm2shielding are larger than the doses received with no shielding.This occurs because of the complexity of electron-induced secondary particles and backscattered electrons.

Table 3.The stopping energies of the equivalents of 1,5,and 10 g/cm2 of aluminum shielding.

3.3.The equivalent dose and the effective dose

The quality factor,Q,of the particles used by the ISS and China’s “Shenzhou” series spacecraft is 1.8.[26]Accordingly,this value is also used in our study.The resulting equivalent doses given to the vital organs at the solar maximum and the solar minimum are shown in Fig.7.The total dose equivalents received by the human phantom with 0 g/cm2, 1 g/cm2,5 g/cm2,and 10 g/cm2of shielding are shown in Table 4.

Fig.7.Organ and tissue equivalent dose rates for a trapped radiation environment with various equivalent aluminum shielding thicknesses:(a)at the solar maximum and(b)at the solar minimum.

Table 4.The total equivalent doses received by the human phantom.

Figure 8 shows the effective doses as a function of the shielding thickness during the solar maximum and minimum.As illustrated by Eq.(7),the effective dose is organ-or tissuerelated,and the tissue weighting factor of skin is 0.04,which is three times less than the weighting value used for organs such as the breast,lungs,stomach,ovaries,and liver.As a result,the effective dose received by the skin is lower than those received by the breast,lungs,stomach,ovaries,and liver at the solar minimum or after a thin layer of shielding at the solar maximum, as shown in Fig.8.The total effective dose absorbed by the whole human body after shielding is shown in Table 5.Figure 8 shows that the effective dose rate absorbed by the reproductive organs of females, including the ovaries and the uterus,is not negligible.It is also the case that the effective dose rate received by the ovaries is smaller than those received by the eyes, lungs, and stomach, but larger than the dose rates of most critical organs after a thin layer of shielding.

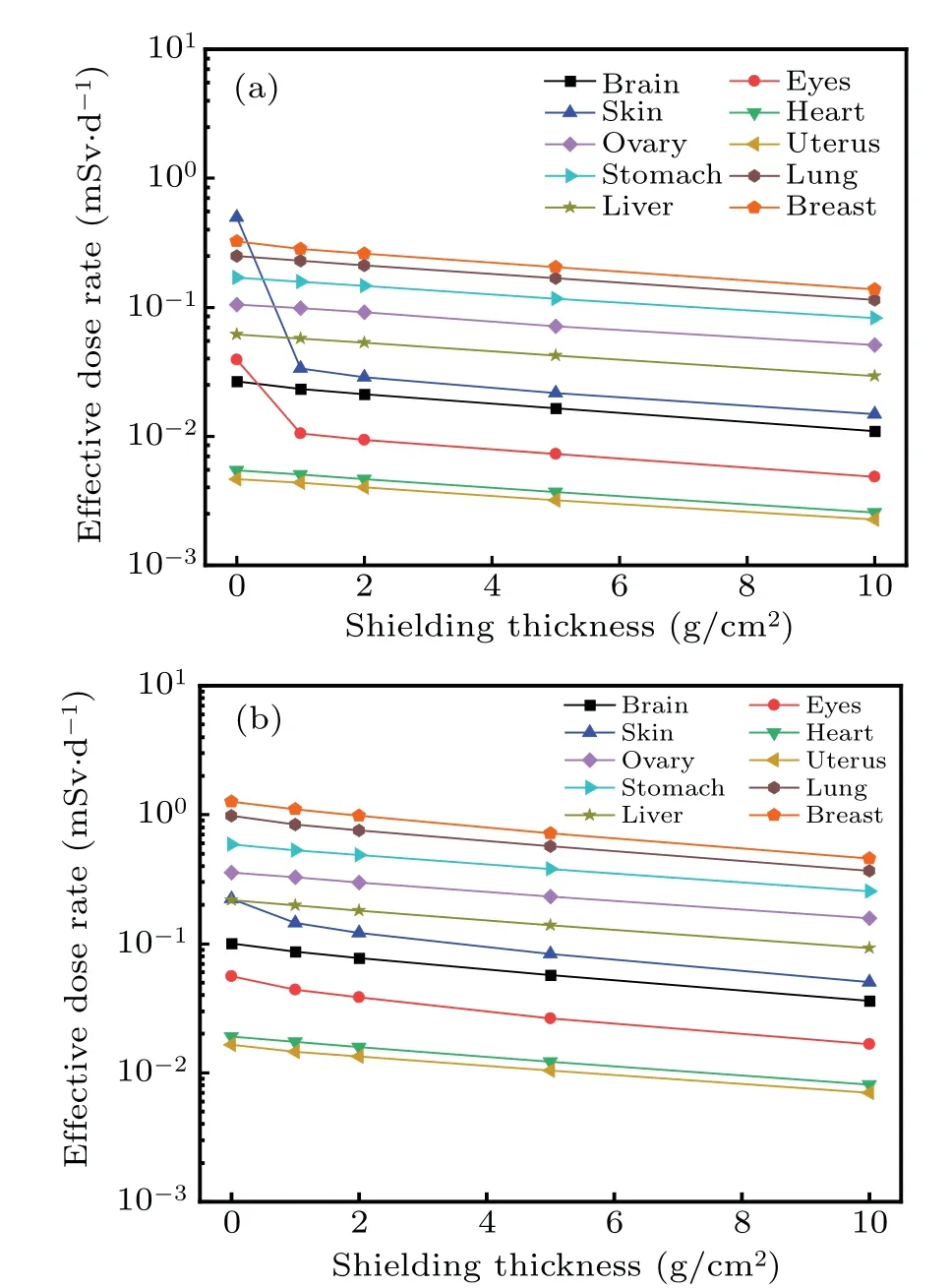
Fig.8.Organ and tissue effective dose rates for the trapped radiation environment for various equivalent aluminum shielding thicknesses:(a)at the solar maximum and(b)the solar minimum.

Table 5.The total effective dose rate received by the human phantom.

3.4.Radiation hazard assessment

The hazards posed to astronauts by space radiation are unavoidable.Various space agencies have proposed astronauts’permissible exposure limits.China has recommended shortterm flying dose limits for the skin,as follows:for Chinese astronauts taking part in LEO missions,the limits are 0.15 Sv for three days,0.20 Sv for seven days,and 0.40 Sv for 30 days.[14]Figure 9 shows the skin equivalent dose received by female astronauts after different thicknesses of shielding during the solar maximum and the solar minimum and the equivalent radiation dose limits for Chinese flight crews for a 30-day LEO mission.Trapped radiation deposits a large dose of radiation in the skin when it is slightly shielded.The radiation dose behind 1 g/cm2shielding exceeds 400 mSv at the solar minimum.However,such a low level of shielding is equivalent to space suit shielding, which is only modeled for extravehicular activity and makes up a small proportion of an astronaut’s time in space.To ensure that the effective doses received by astronauts stay below the radiation limits,2 g/cm2of shielding is required.

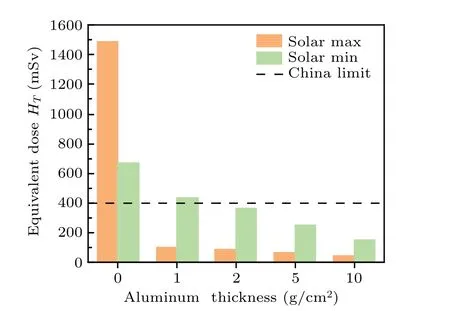
Fig.9.A comparison of the results for the 30-day LEO flight skin equivalent dose limit.

As is well known,the radiation exposure risk is age-and gender-specific due to latency effects, differences in tissue types and sensitivities, and differences in average life spans between genders.NASA used career effective dose(E)limits for a REID=3%for missions that had a duration of one year or less.NASA also adopted a career effective dose limit of 470 mSv for 30-year-old female astronauts.[27]Figure 10 compares this limit for a one-year mission and the effective doses induced by trapped radiation after different shielding thicknesses.This effective dose rate is always far less than the dose limits under solar maximum conditions.However, under solar minimum conditions, the organ-equivalent dose value exceeds NASA’s limits when the shielding thickness is less than 5 g/cm2.The total effective dose is estimated to be 0.36 Sv for female astronauts after 5 g/cm2of shielding.These results are also consistent with the recommendation of the Chinese National Standard of Radiation Protection requirements for spacecraft crew modules (ID: GJB 4018-2000) that the thinnest mass shielding thickness of the crew cabin should not be less than 2 g/cm2.

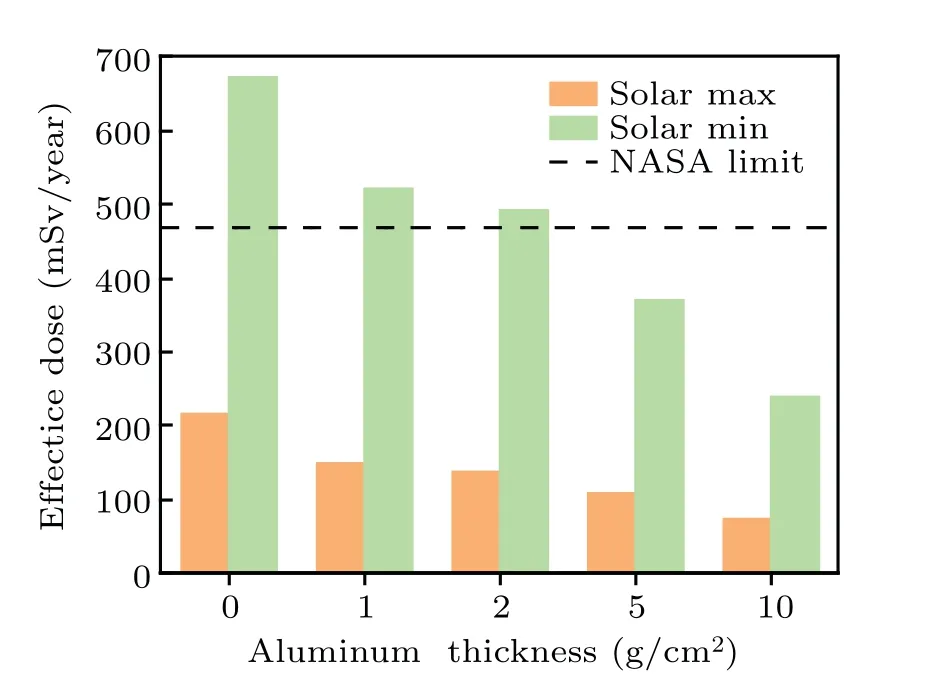
Fig.10.Comparison between the one-year mission effective dose and the NASA limit.

4.Conclusions

In this paper, we took a Chinese female voxel phantom with a height of 158 cm and a weight of 54 kg as a model and discussed the absorbed dose,the dose equivalent,as well as the effective dose received by the female voxel phantom and the critical organs for different levels of shielding of the Tianhe core module in flows of trapped radiation during the solar maximum and the solar minimum.The shallow organs,including the skin and eyes, received larger doses and larger equivalent doses,while the effective dose received by the skin was lower than those of the other critical organs listed in this paper.Without shielding, the doses received by the shallow organs were mainly produced by trapped electrons.When a thin layer of shielding was employed, the doses were mainly induced by trapped protons.Inner-organ doses mainly originated from trapped protons.For female astronauts, the effective dose rate received by the ovaries was larger than those received by most of the critical organs.

In addition, the risk of space-radiation exposure was assessed by comparing the doses with the current risk limits published by China and NASA.The results show that for 30-day LEO missions,the effective doses received by astronauts after 2 g/cm2shielding are guaranteed to remain below the radiation limit of 0.40 Sv proposed by China.After 5 g/cm2of shielding,the effective dose received by female astronauts is 0.36 Sv for a one-year mission.This value is below NASA’s career effective dose limit for 30-year-old female astronauts.In summary, the results of this paper are in agreement with the recommendations of both the Chinese National Standard of Radiation Protection and NASA.Hence,the results and methods of this work can be used to guide and optimize the radiation protection provided for space missions.Female astronauts are exposed to more radiation risks by flying in space.More detailed work should be conducted for female astronauts.In addition,a preliminary study has been proposed to investigate the equivalent biological dose and effects of high-energy heavy ions,such as Fe ions,[28]for which further study should be carried out.

Acknowledgements

Project supported by the Open Project Funds for the Key Laboratory of Space Photoelectric Detection and Perception(Nanjing University of Aeronautics and Astronautics), the Ministry of Industry and Information Technology of China(Grant No.NJ2022025-7) and the Fundamental Research Funds for the Central Universities(Grant No.NJ2022025).