Machine learning of turbulent transport in fusion plasmas with neural network

Hui LI (李慧), Yanlin FU (付艳林), Jiquan LI (李继全)and Zhengxiong WANG (王正汹)

1 Key Laboratory of Materials Modification by Laser, Ion, and Electron Beams (Ministry of Education),School of Physics, Dalian University of Technology, Dalian 116024, People’s Republic of China

2 Southwestern Institute of Physics, Chengdu 610041, People’s Republic of China

3 School of Physics, Dalian University of Technology, Dalian 116024, People’s Republic of China

Abstract Turbulent transport resulting from drift waves, typically, the ion temperature gradient (ITG)mode and trapped electron mode(TEM),is of great significance in magnetic confinement fusion.It is also well known that turbulence simulation is a challenging issue in both the complex physical model and huge CPU cost as well as long computation time.In this work, a credible turbulence transport prediction model, extended fluid code (ExFC-NN), based on a neural network (NN) approach is established using simulation data by performing an ExFC, in which multi-scale multi-mode fluctuations, such as ITG and TEM turbulence are involved.Results show that the characteristics of turbulent transport can be successfully predicted including the type of dominant turbulence and the radial averaged fluxes under any set of local gradient parameters.Furthermore,a global NN model can well reproduce the radial profiles of turbulence perturbation intensities and fluxes much faster than existing codes.A large number of comparative predictions show that the newly constructed NN model can realize rapid experimental analysis and provide reference data for experimental parameter design in the future.

Keywords: neural network, plasma turbulence, transport properties, plasma simulation

1.Introduction

Experiments, simulations and theoretical studies in magnetic confinement fusion have conclusively shown that plasma confinement performance is mainly governed by turbulent transport, which is caused by many types of plasma turbulence, typically, micro-scale fluctuations, e.g.the ion temperature gradient (ITG) mode and trapped electron mode(TEM) in current fusion devices.Great progress has been made in understanding the physical mechanism of the transport phenomenon in tokamaks.Furthermore, many kinds of Alfvénic waves,such as the toroidal Alfvénic eigenmode and the energetic particle mode,and even multi-scale multi-mode fluctuations may play an essential role in burning plasma confinement in future fusion reactors like DEMO [1] and ITER [2].Note that understanding complex turbulent transport highly relies on massive parallel simulation even though some significant advances in fusion plasma turbulence theories have been achieved based on gyrokinetic formalism.The related codes have been widely developed to study the properties of ITG and TEM [3] turbulence.In addition,transport behavior in the experiments is analyzed [4].Direct numerical simulations have successfully provided tremendous insight into the underlying transport physics, and they are currently a powerful tool in transport study.

Although these first-principles-based models have successfully described transport process in the core plasma under some conditions, they are still computationally challenging,that is, they are time-consuming, require intensive computation, have high CPU cost, etc.In particular, gyrokinetic simulations hardly last up to the quasi-steady-state phase and their numerical accuracy is usually low for edge plasmas [5].Except for the gyrokinetic approach, a fluid model is also established to simulate turbulence transport including ion and/or electron-scale physics.Generally, when kinetic electron is involved in the simulations, the calculation time is greatly increased.Even if it is running on a high-performance super-computer system, it still takes from several hours to days to obtain valid results.Using such a simplified theoretical model, the speed of calculation could be significantly increased and it has proved to be effective to a large extent in the tokamak plasma core [6–9].However, for turbulence transport with a global effect, computation based on reduced physical models is still rather time-consuming.On the other hand, using well-known conventional empirical models and/or confinement scaling laws [10], the physical properties could be well understood with the easy implementation.However, they were all limited to zero-dimensional system analyses without radial profiles for plasma parameters.Therefore, both fast and accurate prediction models on turbulent transport are essential for the illustration and optimization of current experimental operation scenarios as well as for real-time operation control by performing fast integrated modeling.They may further be applied to extrapolate probable parametric regimes in future devices.Hence, the development of new transport models and the improvement of existing models are badly needed to illustrate the properties of turbulence and provide consultations for the design of future tokamak reactors.

To date, machine learning with a neural network (NN)method has been applied in fusion plasma research, for instance,nonlinear regression for energy confinement scaling[11], database establishment of neoclassical transport [12],rapid nonlinear determination of equilibria parameters [13],reconstruction of electron temperature profile [14], chargeexchange spectrum analysis on the JET device [15], classification of disruption [16–18] and the onset of L-H transition[19].To analyze what physical mechanisms play roles in energy confinement, several works have developed new transport models, which have adopted NNs to predict the distribution of electron and ion heat flux.In the work [20], a database based on campaigns of DIII-D experiments from 2012 to 2013 was built.It has been found that the NN method could well reproduce the experiment phenomenon within most of the plasma radius or even across a broad range via training and testing the NN model.The radial distributions of the heat flux were smooth, which indicated that the solution found by the NN model was a smooth function of the set of local input parameters, although each of the radial positions was simulated independently of the others.This numerical method was effective and took only a few CPU-μs per data set.Therefore, it was most suitable for further application of scenario development and real-time plasma control.Through further research, they developed two NN-based models to predict the core turbulent transport process and reproduce the pedestal structure[21].It was verified that the NN method can reproduce the output results of TGLF and EPED1,which are theory-based models, by speeding up the calculation process.Pathak et al revealed that it was effective to use machine learning to make model-free predictions for arbitrary spatiotemporal chaotic systems.The system was characterized by a large spatiotemporal range and the dimensionality was entirely derived from the evolution process of the system itself [22–24].A transport model established by Citrin et al aimed to predict the turbulence transport in a tokamak core with real-time capabilities.A multi-layer perceptual NN was used in the study, which successfully predicted the transport flux output by the original quasi-linear gyrokinetics codes,while greatly shortening the calculation time.The 300 s ITER discharge process within 10 s could be done with this model.This kind of regression principle verification based on the transport model proved the possibility of greatly expanding the dimensionality and physical authenticity of the input parameters in future training [25].It can increase the calculation speed of plasma real-time control and integrated simulation applications.Plassche et al proposed an ultra-fast NN model, namely QLKNN, which had the ability to predict the heat flux and particle flux[26].QLKNN is a surrogate model of QuaLiKiz, which is a quasi-linear gyrokinetic transport model.The database used for NN training was calculated by QuaLiKiz.Narita et al used a semi-empirical method to estimate quasi-linear particle transport,and established a rapid transport model that predicted the density peaking through a NN method[27].Based on the above work,it was found that the NN model has the following advantages.On the one hand,the numerical solution of the analytical formula is several orders of magnitude faster than the calculation of the original program.On the other hand, the calculation time required to compile the database has nothing to do with the calculation time spent in the tokamak simulation itself.At the same time,it is proved that the NN model can contain more complete numerical results than the current transport model, while saving calculation cost.

This work proposes a NN model,known as the extended fluid code neural network (ExFC-NN), that can predict the physical properties of turbulent transport in real time with a change of plasma parameters in tokamak plasmas.First, we build databases based on the simulation results using the ExFC.ExFC is a fluid-type turbulence transport code based on the Landau-fluid model extending to cover the TEM physics to study tokamak plasma multi-mode multi-scale turbulence dynamics.At present, the code has been well developed with multi-mode character including the largescale magnetohydrodynamic resistive tearing mode, ITG mode, TEM and kinetic ballooning mode.The basic model equation system of ExFC applied in this work aims to describe the physical properties of turbulent transport,including the types of dominant turbulence (including ITG,TEM and coexisting ITG and TEM), radial averaged flux(including particle fluxΓ, ion heat fluxQi,electron heat fluxQe), radial distribution of perturbations (including ion temperatureTi(r) ,electron temperatureTe(r) ,densityn(r)) and radial flux distribution(Γ(r),Qi(r),Qe(r)).The databases are built with these physical quantities and then employed to train a multi-layer feed-forward NN.The NN inputs, which have been standardized, are a set of global dimensionless plasma parameters.Furthermore, the applications of the NN model are extended to predict all the fluxes including both local and global effect and corresponding fluctuations.The well-trained NN model shows sufficient ability to reproduce the same simulation results, and can accurately obtain the physical characteristics of tokamak turbulence at a computational cost of only a small amount of CPU time.

The rest of this paper is organized as follows.In section 2, the theoretical method of NN modeling is introduced.Section 3 focuses on the prediction results, including the main turbulence type, radial averaged flux, radial profiles of fluxes as well as the corresponding perturbations in the nonlinear phase.This further illustrates the effectiveness of the transport model in predicting linear and nonlinear physical processes.A summary and the outlook for future work are provided in section 4.

2.Methods

Turbulent transport in magnetically confined fusion plasma is one of the obstacles to realizing fusion energy.High-temperature fusion plasma turbulence is characterized by multiple perturbation modes (originating from different driven mechanisms) with multi-scales (from macroscale, mesoscale to micro-scale), etc.The highly nonlinear interaction and complex magnetic configuration are a great challenge to numerically simulating global turbulent transport, in which solving the overall evolution of physical quantities with time is usually required.Note that long-time global simulation based on first-principle gyrokinetic theory, e.g.the so-called full-f algorithm, while it is of high precision, is very challenging in terms of calculation method and economy.Simulation based on an improved fluid model (such as the Gyro-Landau-fluid model) is an alternative and available choice.In this work, an improved Gyro-Landau-fluid model governing the ITG mode with extension to cover the trapped electron dynamics,described by the so-called Weiland model[28, 29], is adopted to numerically simulate global turbulent transport.Here, a set of five-field fluid equations is advanced to describe the evolution of global electrostatic ITG and TEM turbulence as follows:

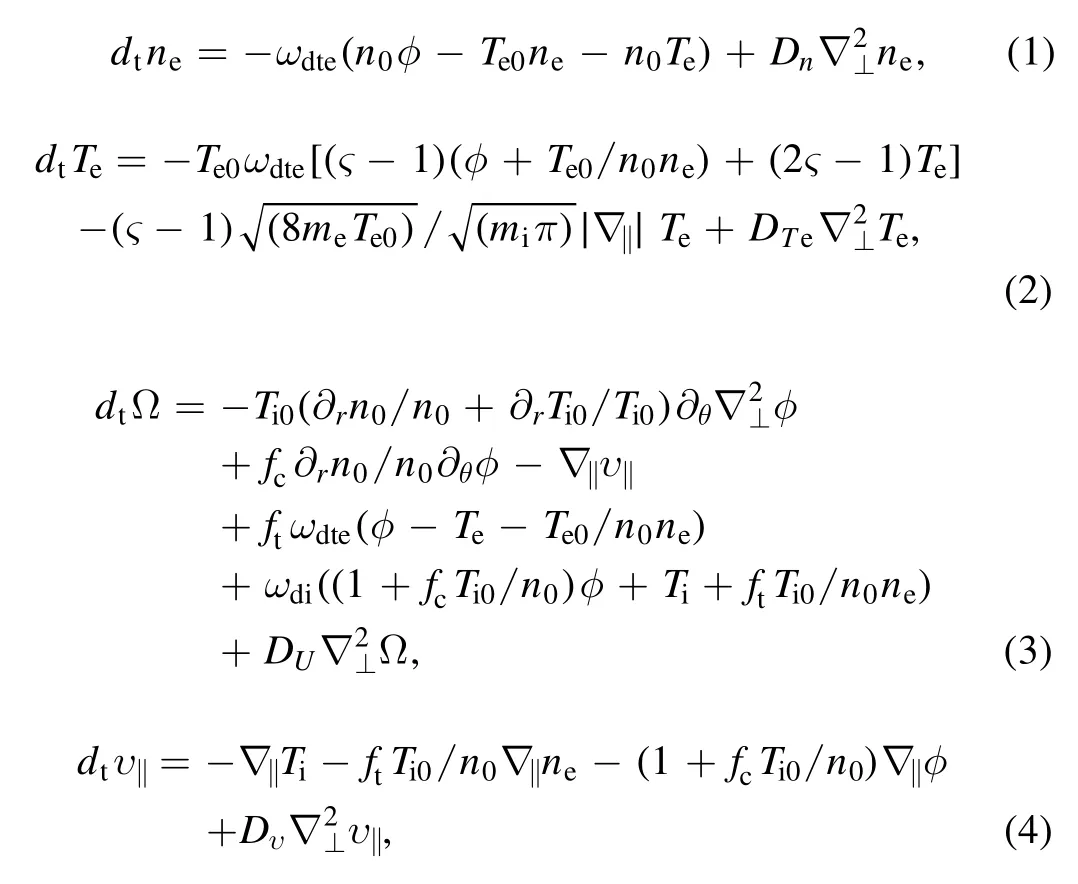
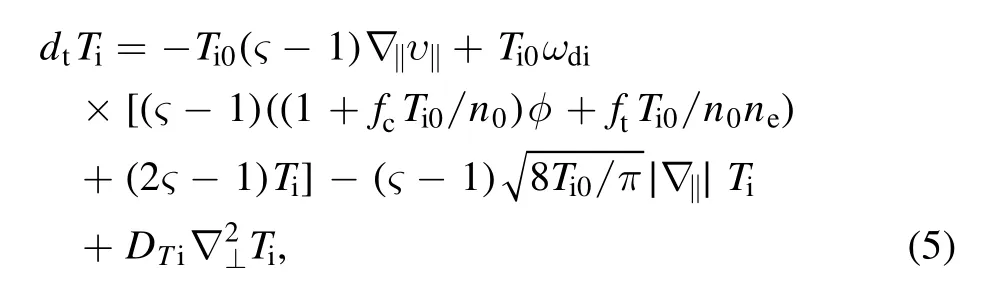
wherene,Te, Ω,v‖andTiare, respectively, plasma density,electron temperature, vorticity, parallel ion velocity and ion temperature.The definition and notation of all quantities as well as the normalizations are conventional.The governing equations can be solved by employing the initial value code ExFC, which has been perfectly benchmarked linearly and nonlinearly [30, 31].Figure 1, the evolution of electron heat fluxQe,is displayed as an example here.

After solving a series of discrete physical quantities using the ExFC, mathematical methods are considered to generate the function of a certain physical quantity in analytical form in order to quickly and accurately obtain the transport features under any set of plasma parameters.Considering the form of the function, it can generally be divided into two categories,namely interpolation and fitting.Interpolation is a statistical method to estimate an unknown value of the data point using the known values of the data points around it.Curve fitting is the process of constructing a curve or mathematical function that provides the best match to a series of data points,possibly subject to some constraints.One of the interpolation methods commonly used is cubic spline interpolation.However,when the input dimension increases, the amount of data required increases sharply.Generally, the spline interpolation method is only suitable for low-dimensional systems.Compared with interpolation, the fitting approach is much more flexible.Nevertheless, in this high-dimensional system, a common shortcoming of ordinary fitting methods is the accuracy of fitting.Hence, NN, essentially as a function fitting method,has been widely developed.It is also regarded as an implementation of artificial intelligence.The forms of NNs are diverse,such as recurrent NNs,convolutional NNs,etc.They are all universally used in different fields, such as machine learning and artificial intelligence [32–34].The functional form of the NN is quite flexible.Therefore,in theory,the NN can be used to fit the functional form with any shape[35]and a higher fitting accuracy can be achieved.Moreover,our goal is to find an analytical formula that can quickly and reliably reproduce the physical quantities output by the ExFC.In summary,in this work,we choose the NN fitting method and select the feed-forward approach with setting up multiple layers with adjustable variables (including weights and biases) accompanied with general approximation characteristics[36].The linear combination of input and bias is propagated through a series of nonlinear vectors of transfer functions(namely the hidden layer)until the final linear combination is transmitted to the output layer.The feed-forward NN structure [37] selected in this work has two hidden layers connecting the input layer and output layer,denoted as I–J–K–1,which means that there are I nodes in the input layer with one node in the output layer.The form of the NN function can be written as,

wherej= 1,… ,J;k= 1,...,K;x i(i= 1,… ,I) is taken as the input vector andyis the output of the NN function.The weightsare connected to the jth neuron in the (l- 1) th layer and the ith neuron in the lth layer.The excitation functions of the neuron aref1andf2, which are formed as the hyperbolic tangent functions.bnandxiare the bias vector and input value vector, respectively.Since the data volume and complexity of different physical quantities change in detailed simulations, the number of neurons in the hidden layer is changed at the same time.This will be introduced separately in the next section.

In the training process, the Levenberg–Marquardt algorithm [38] is applied to optimize the parameters of the NN model.The accuracy of the fitting can be expressed by the root mean square error (RMSE).In order to improve the fitting accuracy,we adopt the‘early stopping’approach[39]to avoid overfitting.We randomly selected 95% of the data points as the training database with the remaining 5% as the validation set.To further reduce the random errors, the final ExFC-NN is obtained by averaging over three NN fits with the smallest RMSE.The RMSE expression is as follows:

3.Numerical results with the ExFC-NN model

Based on the above discussion and combined with the characteristics of the database, the double hidden layer feed-forward NN is finally selected in this work.In this NN topology,information starts to propagate from the layer of input neurons and goes through two hidden layers.Finally,it is passed out of the output layer.Once the relationship between input and output layers is found on the training data set, the NN model can be used to predict the output of similar inputs.Furthermore, some points are also taken outside the database to verify the accuracy of the ExFC-NN.After establishing a credible ExFC-NN model, this section focuses on the applications of the model.

First, the trained ExFC-NN model is applied to predict the type of dominant turbulence, ITG or TEM or coexisting ITG and TEM, transformed by changing the gradients of three key parameters: plasma density, ion and electrontemperatures.To establish the database,a total of about 2800 cases were selected for the NN training and validation set according to the steps in figure 2.The NN topology here is 3-8-11-1,which means that two hidden layers have 8 neurons and 11 neurons, respectively.The schematic diagram is shown in figure 3.The input of the NN is a series of parameters describing the characteristic length including the density gradient(R/Ln),ion temperature gradient(R/LTi)and electron temperature gradient(R/LTe),while the output layer of the NN is a type of dominant turbulence, namely, ITG,TEM or ITG and TEM.After the training process, the prediction results based on the NN model are compared with the simulation results of the ExFC.The correct rate of turbulence type prediction is displayed in table 1.It is shown that this method can effectively classify these three types of data.The intuitive comparison result is shown in figure 4.With the increment ofR/LTi, the type of instability changes from TEM-dominated to ITG-dominated, which is consistent with the ExFC simulations.We firmly believe that when any set of gradient parameters is given,the type of dominant turbulence in the nonlinear phase can be directly and effectively judged,along with saving calculation time and cost.In other words,a faster method for parameter design can be provided.

Figure 2.Schematic diagram for the construction of simulation results based on the ExFC in order to obtain a reliable ExFC-NN model.

Figure 3.Schematic of the NN topology for the prediction of the dominant turbulence.

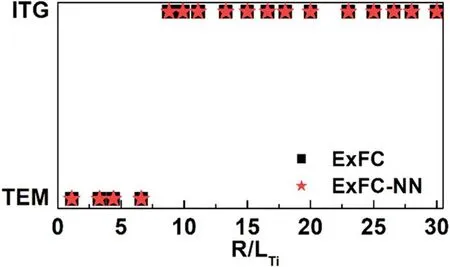
Figure 4.Comparison of the type of dominant turbulence obtained from ExFC simulations (squared) and ExFC-NN modeling predictions(star)as a function of R /LTiwith R /L Te = 8,R /L n =1.Test data are outside the database.

Table 1.The accuracy of classification via ExFC-NN model.

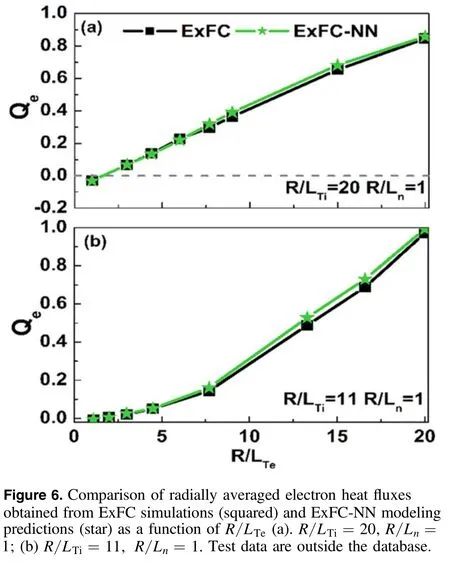
Second,the ExFC-NN model is considered to predict the averaged flux under any parameters.Shown in the introduction, ExFC as a transport simulation code, is mainly used to analyze the turbulence transport process.For different gradient parameters, the transport properties change very obviously.Furthermore, the study of anomalous transport involving parameter scanning usually takes a long time.Here,we take the prediction of the radial averaged value of the electron heat transportQeas an example to illustrate the effectiveness of the NN model.Figure 5 shows the 2D regression distribution ofQeobtained by the NN model prediction and ExFC simulation within the training domain(R/Ln,R/LTe,R/LTi) =[1 → 20; 1 → 20; 1 →30].The regression coefficient R2= 0.98also quantitatively illustrates the accuracy of this prediction method.Comparison between the predicted value of the NN-based model and the ExFC simulation result are directly shown in figure 6.The relative error of figure 6(a) is less than 5%, which shows that the characteristics of the inward heat flux of electrons can be predicted.The relative error calculated in figure 6(b) is less than 8%.In particular,the NN-based model can also perfectly predict a typical physics phenomenon whereQeincreases suddenly asR/LTerising to a certain threshold.Similar predictions can also be made for averaged particle fluxΓ and ion heat fluxQi(which are not plotted here).It is worth mentioning that particle pinch (namely, the particle flux is negative)occurs in a certain parameter regime,and the NN model can also accurately reproduce it.

Third,besides predicting the averaged flux shown above,the developed ExFC-NN model can take into account the global effect of turbulent transport.For this feature, we predict the radial profiles of fluxes and related perturbations.Global transport means that the flux at a fixed radial position does not only depend on local parameters at the same radial position.In this case, each input/output of the NN model requires multiple neurons for us to understand the plasma parameters at multiple locations across the whole plasma radius, and about 2700 ExFC simulation data sets randomly selected from the database (including the selected radial 64 grid data) are used as the training base to train the network.Here, the input is the initial radial distribution(Ti0(r),Te0(r),n0(r)) instead of the dimensionless gradient value and the NN topology is 7-40-40-1.The training result of the radial profile of ion temperature perturbationTi(r) is shown in figure 7.Figure 7(a) is a 2D regression distribution diagram of the predicted values of the NN model and the results of the ExFC simulation.The regression coefficient is R2= 0.99, indicating that the training precision is good.Figure 7(b) shows the radial profile ofTi(r) under random initial distribution, andTi(r) is successfully predicted in the nonlinear phase with a relative error of less than 0.4%.At the same time,the same processing is done for the density profilen(r) and the NN topology remains unchanged.As shown in figure 8(a), the 2D regression distribution graph with a high regression coefficient R2= 0.99also indicates perfect training results.Figure 8(b) exhibits that the results of the ExFC and NN are basically the same and the relative error is less than 0.7%.It is worth focusing on the fact that the profile given in figure 8(b) shows that in the nonlinear stage under this parameter, the density perturbation is relatively obvious and the NN model can fully capture the change in the whole radial direction.

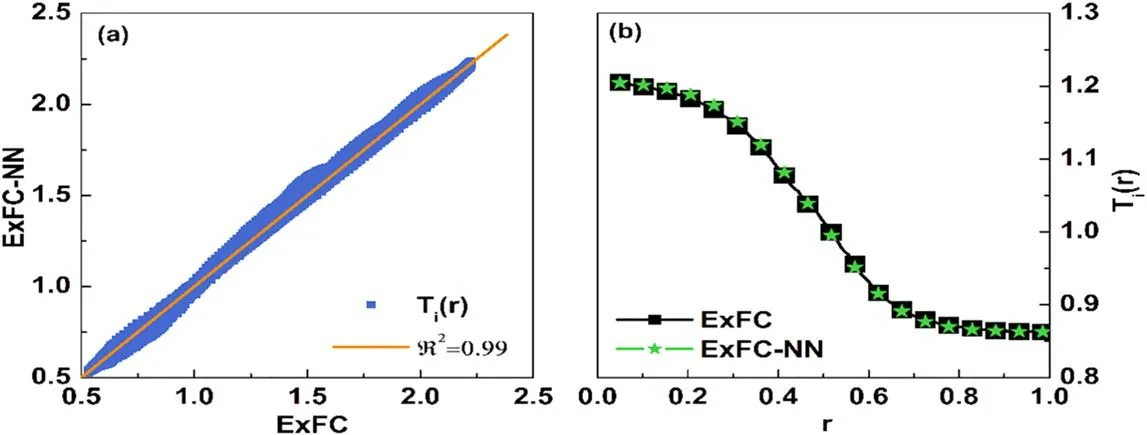
Figure 7.(a)Regression histograms of Ti (r)comparing the ExFC-NN approach and ExFC simulations,R2 is the coeffciient of determination;(b)comparison of Ti (r)obtained from ExFC simulations(squared)and ExFC-NN modeling predictions(star).Here,the test data are outside the database.

Figure 8.(a)Regression histograms of n (r)comparing the ExFC-NN approach and ExFC simulations,R2 is the coefficient of determination;(b)comparison of n (r)obtained from ExFC simulations(squared)and ExFC-NN modeling predictions(star).Here,the test data are outside the database.

Finally,the ExFC-NN model is trained to produce radial profiles of fluxes.Figure 9 shows the prediction results of the radial profile of ion heat fluxQi(r).The topology is 7-50-80-1 and the regression coefficient R2= 0.99is calculated, as shown in figure 9(a).The comparison result of the ExFC and NN models is plotted in figure 9(b),showing that the relative error is less than 8%.Since the gradient mainly locates at the position ofr= 0.5,the maximum value of the flux falls in the same position.It can be seen from figure 9(b)that the error of the prediction result nearr= 0.5 is small.Similarly, for the radial profile of the electron heat transportQe(r) ,as shown in figure 10, the prediction result is comparable with the ExFC simulation result with a low error.The topology here is transformed into 7-50-70-1.

Figure 9.(a) Regression histograms ofQi (r) comparing the ExFC-NN approach and ExFC simulations, R2 is the coefficient of determination;(b)comparison ofQ i(r)obtained from ExFC-NN modeling predictions(star)and ExFC simulations(squared).Here,the test data are outside the database.

Figure 10.Comparison ofQ e( r) obtained from ExFC-NN modeling predictions(star)and ExFC simulations(squared).Here,the test data are outside the database.

4.Conclusion

In this work, a credible NN transport model, ExFC-NN, is established to predict the type of dominant turbulence and associated transport property.ExFC-NN is suitable for the electrostatic ITG and TEM turbulence.The database for training the ExFC-NN is built based on the simulation results performing the extended fluid code ExFC.The well-trained ExFC-NN model is able to perfectly reproduce and predict what the ExFC simulation can do,and the calculation speed is much faster than the latter one.In detail,the NN model can be used to predict the type of dominant turbulence, radially averaged fluxes, and radial profiles of electron temperatureTe(r) ,ion temperatureTi(r) and densityn(r) as well as the corresponding electron heat fulxQe(r) ,ion heat fluxQi(r)and particle fluxΓ(r).All accuracies are within acceptable ranges.Most importantly, it is shown that the ExFC-NN model not only has the ability to predict the radial local changes of perturbations, but can reproduce inward transport, for instance,particle pinch.Therefore, the ExFC-NN model is expected to realize rapid turbulent transport-related experimental analysis of the HL-2A fusion device.It may also provide a data reference for the design of experimental parameters.The relevant analysis will be further presented in future work.

Although the applications of the present ExFC-NN model have exhibited perfect feasibility and fast calculation speed as well as sufficient accuracy, there are still numerous possibilities to advance the model by improving the NN algorithm and expanding the dependence of more relevant parameters,especially in the quasi-steady nonlinear stage.On one hand, more essential plasma parameters, such as the inverse aspect ratioε,safety factorqand magnetic shearscan be involved as input parameters in the NN model.On the other hand,some typical features of turbulence and associated transport obtained from the ExFC simulation can be collected into the database.For instance, the spatiotemporal evolution of the density and heat fluxes could be well predicted by the ExFC-NN model if the characteristics of the turbulence structure are taken as the input parameter.Furthermore, the ExFC-NN model can be applied to analyze nonlinear dynamics, such as Dimits shift [40].At the same time, it will work well to establish a NN model including electromagnetic effects, which may be of much significance with regard to computational efficiency and cost.

Acknowledgments

This work was supported by the National Key R&D Program of China (Nos.2017YFE0301200 and 2017YFE0301201)and partially by National Natural Science Foundation of China (Nos.11775069 and 11925501), the Fundamental Research Funds for the Central Universities (No.DUT21GJ205) as well as the Liao Ning Revitalization Talents Program (No.XLYC1802009).