压电双材料反平面问题的界面裂纹分析*

梅 杰 李 杨 李立杰 陈定方 宋 钢

武汉理工大学交通与物流工程学院 武汉 430063

0 引言

压电材料具有机电耦合性，即力载荷可引起材料变形，进而引起电场的改变，同时电场也会引起变形使应力和裂纹尖端撕开位移发生改变，这种特性使其在现代工程中具有广阔的应用前景。研究表明，在多层压电元件中，由于界面处材料成分和性质的突变，常常导致界面处应力集中，使界面处出现开裂或蠕变现象，从而大大缩短了压电元件的使用寿命[1]。界面裂纹开始扩展的应力强度因子临界值小于相应的2 种单材料临界值，在相同的临界值作用下，界面裂纹的扩展速率高于相应2种单材料的扩展速率。由此可见，界面是一个较薄弱的环节，与界面处的杂质、孔洞等缺陷存在一致，这些缺陷对界面疲劳性能的弱化有很大影响。

压电材料的研究多集中在单压电材料断裂和裂纹尖端场的各类强度因子，而对压电双材料的界面损伤研究较少，对正交各向异性压电双材料的界面端裂纹应力分析则更少，故研究压电双材料界面裂纹意义重大。Wang X 等[2，3]研究了面外机械载荷作用下2 种不同压电材料界面上的导电裂纹，发现了裂纹尖端的振荡平方根奇异性，同时定义了一个复杂的电弹场浓度矢量以表征裂纹尖端附近的奇异场，并导出了能量释放率的简单表达式；Pak Y E[4]对压电双材料中动态扩展裂纹的近尖端应力和电位移场进行了解析求解，推导了裂纹张开位移和电位跳跃关于应力和电位移强度因子的显式表达式，导出了压电双材料中的界面裂纹与路径无关的分离动态J 积分；Choi S R 等[5，6]考虑了在机电载荷作用下2 个不同的横观各向同性压电材料之间的3 个共线界面裂纹问题，得到了应力强度和电位移强度因子的闭式解；Gherrous M等[7]分析了反平面机械载荷和平面内电载荷作用下的半无限大双压电双材料反平面界面三阶Griffith 裂纹问题，利用傅立叶变换法，将压电方程转化为奇异积分方程组，并用切比雪夫多项式进行数值求解，得到应力强度因子和电位移强度因子，并分析了材料参数对裂纹的影响；Lapusta Y 等[8]分析了双材料在反平面机械和平面内电载荷作用下的界面裂纹，导出了裂纹面的剪应力、电场和机械位移跳跃的简单解析表达式，发现了剪切应力、电场和电位移跳跃的奇异点，其强度因子也被确定；Onopriienko O 等[9]考虑了在面外机械载荷和面内电场作用下裂纹面处具有多种边界条件的裂纹，得到了压电材料界面在反平面机械和平面电载荷作用下导电裂纹的键区模型。目前，尚未有关于含界面裂纹的半无限压电双材料结构的电弹性行为的主要工作。

本文研究了含界面边裂纹的压电双材料在2 种组合机电载荷电场作用下压电双材料界面裂纹的扩展情况。利用边界配置法，求出了压电介质为横观各向同性的压电双材料的应力强度因子和能量释放率的表达式，并从材料属性、边界条件和边界配置法3 个方面分析了影响应力强度因子和能量释放率的因素。相比Nishioka T 等[10]导出的J 积分，本文得到了界面裂纹扩展的应力强度因子和能量释放率；文献[7]～文献[9]只给出了应变、电场、应力和电位移中部分表达式，本文得到了应变、电场、应力和电位移的解析表达式；界面模式Ⅲ裂纹在半平面结构(2 种不同厚度的粘结压电材料在力—电载荷作用下)的情况尚未研究。

1 正交同性反平面问题的基本方程

对于反平面问题，位移和电场强度分量为

控制微分方程为

式中：c44为弹性常数，e15为压电常数，Y11为介电常数，φ为电势，2为拉普拉斯算子。

对于一般的压电材料，存在以下关系

将式（3）带入式（2）可得

应变和电场强度分量为

本构方程为

正交异性压电双材料板反平面界面端裂纹如图 1，xoy平面为正交同性界面；C44[1]、e15[1]、Y11[1]为压电介质Ⅰ的材料常数，C44[2]、e15[2]、Y11[2]为压电介质Ⅱ的材料常数；在界面上预设了一道边裂纹，a为裂纹长度，b为材料长度，h为材料厚度。

图1 为含边裂纹压电双材料裂纹扩展模型。情况1为模型受到剪应力τyz＝τ0和面内电载荷D0作用；情况2 为模型受到剪切位移γyz＝γ0和面内电载荷D0作用。x轴沿界面方向，z轴为压电材料的极化方向。在此，先分析情况1，得边界条件为

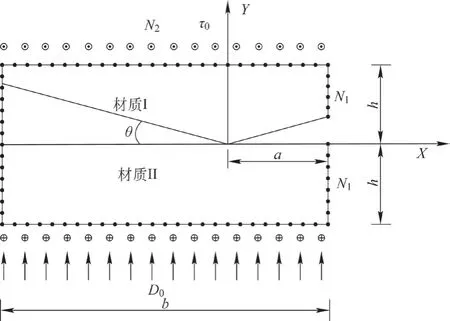
图1 正交同性压电双材料板

当θ＝±π 时

当θ＝0 时

当x＝-a或x＝b-a，∣y∣≤h时

2 横观各向同性反平面问题的解

在式中，i取1、2，分别表示压电材质Ⅰ、电材质Ⅱ。若要使位移和电势满足式（4），则位移和电势应为

式中：Ain、Bin、Cin、Din分别为待定常数，由具体问题的边界条件确定；λin为特征值，由裂纹面的边界条件和界面处的连续条件来确定。

设uz(r，θ)＝H(r)J(θ)′，φz(r，θ)＝K(r)L(θ)，则式（4）可表示为

在极坐标系下，拉普拉斯算子为

将式(11)带入式(10)得

将uz(r，θ)＝H(r)J(θ)′、φz(r，θ)＝K(r)L(θ)带入式(12)得

由于2 个方程相同，下面以推导其中一个为例，由式(13)的上半式两边同时除以可得

令式（14）等于λi得方程组为

进而通解为

由式(15)得

式(17)为欧拉方程，经欧拉公式推导可得

当r→0 时，，故Nn＝0，可得

将式（16）、式（19）带入uz(r，θ)得

其中

由此，式(20)可进一步写为

同理

将uz（r，θ）和φz（r，θ）分别对y求导得

由式（29）～式（31）解得

考虑到反平面问题，式（33）中略去了对称项，故界面裂纹在压电介质Ⅰ中可得

介质Ⅰ中的应变和电场强度表达式为

介质Ⅰ中的应力和电位移表达式为

在裂纹尖端附近，第一项为主项，其余各项可忽略不计。令K1τ为介质Ⅰ中的应力强度因子，即有

同理，类似的结果也可对压电介质Ⅱ写出。由式（37）可知，在裂尖处应力具有 1/2 阶的奇异性，介质Ⅰ、介质Ⅱ的应力强度因子相同，与文献[11]的结论一致。在此基础上，本文进行了应力强度因子和能量释放率研究，从多方面分析了影响应力强度因子和能量释放率的因素。

用YⅢ表示无量纲的Ⅲ型应力强度因子，即YⅢ＝Kτ/K0，其中。

由此可知边界条件式（7a）、式（7b）与平衡方程均已满足，只有加载条件与式（7c）为满足；可用边界配置法进行求解，从而确定系数通过求出应力强度因子。采用边界配置法求解压电材料的应力强度因子。

同理，在第2 种加载情况下，裂纹尖端附近，第1项为主项，其余各项可忽略不计。令Kiγ（i＝1，2）是介质Ⅰ和介质Ⅱ中的应变强度因子，即

能量释放率G可表示为

进而，继续采用边界配置法求出k1(1)、k1(2)、a1(1)和a1(2)。

如图1 所示，左右、上下半边界的配点数为N1，上下边界的配点数为N2。基本解中的级数取前M项，在一个点上可得到2 个含有2M个未知数的方程；如果2N1+N2的个数与M相等，则可求出2M个未知数。但是，为了避免奇异矩阵或病态矩阵，通常2N1+N2的个数大于M的个数，求最小二乘解。

3 配点数和幂级数个数对应力强度因子和能量释放率的影响

3.1 配点个数的影响

考虑应力强度因子和能量释放率与配点个数N1、N2的变化关系，在第1 种加载情况下的取比值a/b＝0.3，h/b＝0.1，幂级数项数M＝30，τ0＝4.2×106Pa，配点个数2N1+N2由5 变化到60，结果如图2 所示。

图2 配点个数与应力强度因子的关系

考虑能量释放率G与配点个数N1、N2的变化关系，取比值a/b＝0.05，h/b＝1，幂级数项数M＝25，γ0＝6.2×10-5，D0＝5×10-3C/m2，配点个数2N1+N2由5 变化到50，结果如图3 所示。

图3 配点个数与能量释放率的关系

由图2 可知，在第1 种加载情况下，当a/b＝0.05、h/b＝1、幂级数项数M＝25 不变时，边界配点数为5 ～15 时的应力强度因子随边界配点个数的增加从1.326 7 减小到1.311 8；在配点数为20 时应力强度因子增加到1.338 5；在配点数为20 ～35 时，值逐渐减小到1.326 5；当配点数为35 ～60 时，应力强度因子的值基本维持在1.326 5 左右，只有小数点后的三四位在变化。在第2 种加载情况下，当a/b＝0.05，h/b＝1，幂级数项数M＝25，在图3 中能量释放率从配点数为15 时的12.425 4 逐步减小到配点数为30 时的9.078 2；当配点数为30 ～60 时，能量释放率的值基本维持在9.078 2 左右。当N1、N2足够大时，应力强度因子和能量释放率的值基本上不随配点数的改变而变化，说明在边界配点数足够多时其对应力强度因子和能量释放率的影响不大。

3.2 幂级数项数M 的影响

考虑第1 种加载情况下应力强度因子YⅢ与幂级数项数M的变化关系。取比值a/b＝0.3，h/b＝0.1,τ0＝4.2×106Pa，左右两边配点数N1＝20，上边界上的配点个数为N2＝40，幂级数项数M由15 变化到60，可得图4 所示关系。

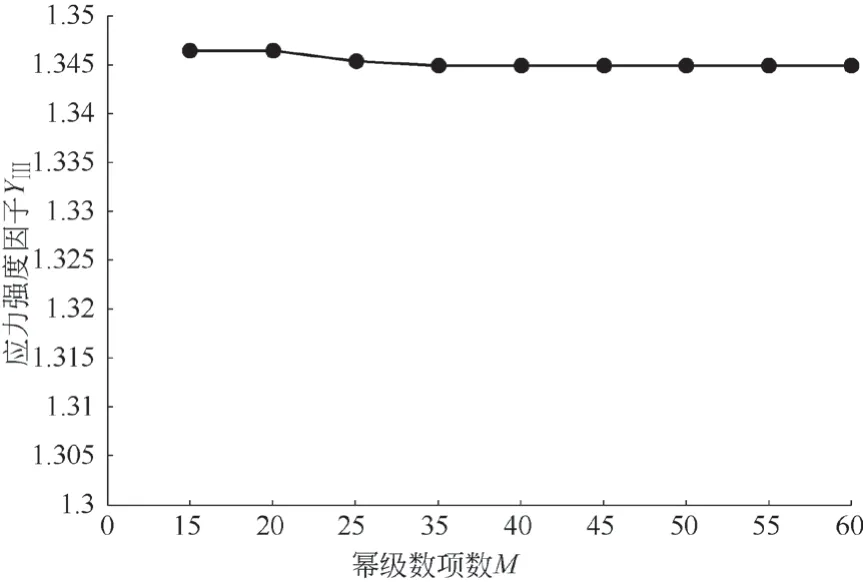
图4 幂级数项数M 与应力强度因子的关系

考虑能量释放率与幂级数项数M的变化关系。取比值a/b＝0.05，h/b＝1，幂级数项数M＝25，γ0＝6.2×10-5，D0＝5×10-3C/m2，左右两边配点数N1＝20，上边界上的配点个数为N2＝40，幂级数项数M由5 变化到60，可得图5 所示关系。

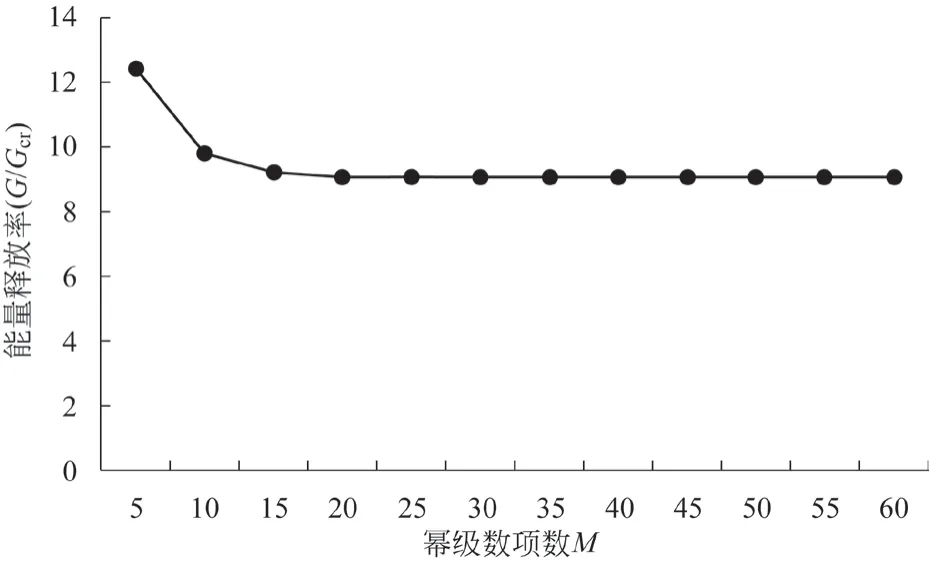
图5 幂级数项数M 与能量释放率的关系

由图4 可知，在第1 种加载情况下，当a/b＝0.3、h/b＝0.1、配点数N1＝20 不变、幂级数项数M在一定范围内变化时，应力强度因子YⅢ的值变化最大幅度为0.013 0，基本不发生变化；当点数较少、应力强度因子出现波动情况、M＝15 ～17 时，应力强度因子增加；当M＝17 ～33 时，应力强度因子持续减小，值到达1.344 9；当M＝33 ～60 时，应力强度因子稳定在1.344 9。由图10可知，在第2种加载情况下，当a:b:h＝1:50:50、a＝0.01 m、配点数N1＝20 不变、幂级数项数M在一定范围内变化时，能量释放率的值由大到小；当幂级数项数较少时，能量释放率的值较大，随幂级数项数的增加值逐渐减小并趋于稳定，这与应力强度因子类似；当幂级数项数增加到22 时，能量释放率的值趋于稳定。

如前所述，边界配置法的收敛性和稳定性是有价值和参考意义的，与文献[12]结论相似。由此，第1 种加载情况下的配点数取30，幂级数项数取33；第2 种加载情况下的配点数取35，幂级数项数取22。

4 应力强度因子的影响因素

4.1 a/b 和h/b 对应力强度因子的影响

压电材料Ⅰ、Ⅱ分别采用PZT-6B、PZT-5H 压电陶瓷，材料常数如表1 所示[13]。

表1 压电陶瓷的材料参数

得到τ0＝4.2×106Pa 时不同a/b和h/b条件下的Ⅲ型应力强度因子，如图6 所示。

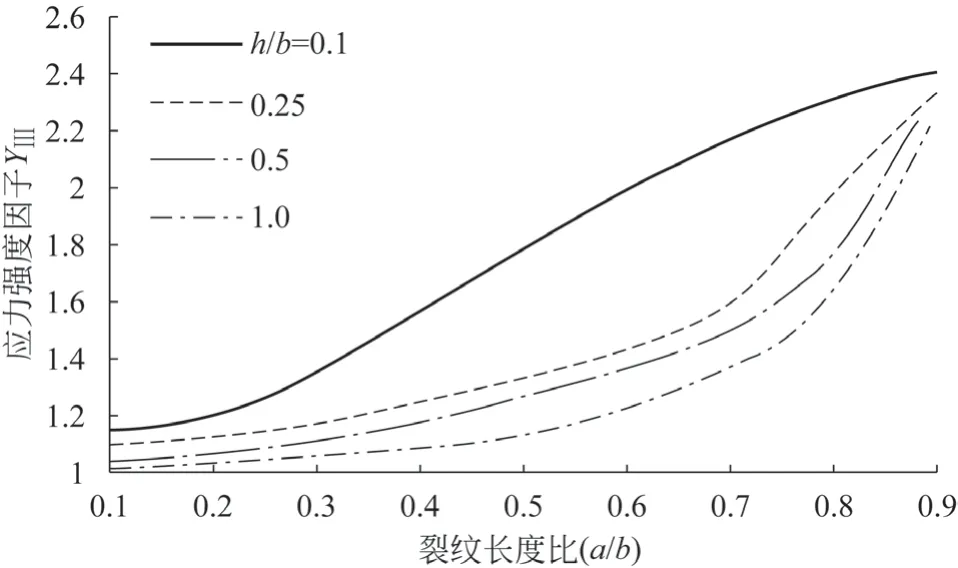
图6 应力强度因子YⅢ在不同a/b 和h/b 条件的值

在图6 中，曲线趋势与文献[14]、文献[15] 对普通材料的分析结果类似。在4 种不同h/b值下，应力强度因子都随着a/b的值增加而增大；4 种h/b比值中，h/b＝0.1 时的应力强度因子最大，h/b＝1 时的应力强度因子最小；在a/b值为0.1、0.9 时，4 种不同h/b的压电双材料尖端应力强度因子差值最小，数值最接近。h/b＝0.1 应力强度因子的变化趋势与其他3 种不同，其他3 种h/b在a/b小于0.7 时的应力强度因子均缓慢增长，且数值较小；当a/b大于0.7时，应力强度因子开始快速增加，而当h/b＝0.1 时，应力强度因子增长速度比其他3 种变化较小；当长度b一定、材料高度h减小时，应力强度因子增加，但高度h的减小对应力强度因子的增加作用大于长度b的增大。

4.2 电位移D0 对应力强度因子的影响

图7 为τ0＝4.2×106Pa、a/b＝0.3 时，不同h/b值的YⅢ随外加电位移D0的变化关系图。本文采用边界配置法分析了矩形横观各向同性压电双材料界面裂纹在反平面剪切载荷和平面内电载荷作用下的电弹性问题，将线弹性断裂力学的传统概念扩展到压电效应，并将结果通过应力强度因子表示出来。由图7 可知，应力强度因子在恒定应力载荷作用下不受电载荷影响，与电位移无关，但受到材料厚度与长度比的影响，厚度比越小，应力强度因子越大。

图7 应力强度因子与电位移D0

5 影响能量释放率的因素

5.1 电位移D0 对能量释放率的影响

图8 为反平面载荷为剪切力时，取不同h/b值的G/Gcr随外加电位移 的变化关系。图9 为反平面载荷为剪切应变时，取γ0＝6.2×10-5、a:b:h＝1:50:50、a＝0.01 m，不同幂级数项数计算出的G/Gcr随外加电位移D0的变化关系图。

图8 反平面载荷为剪切力时能量释放率G 与D0 的关系

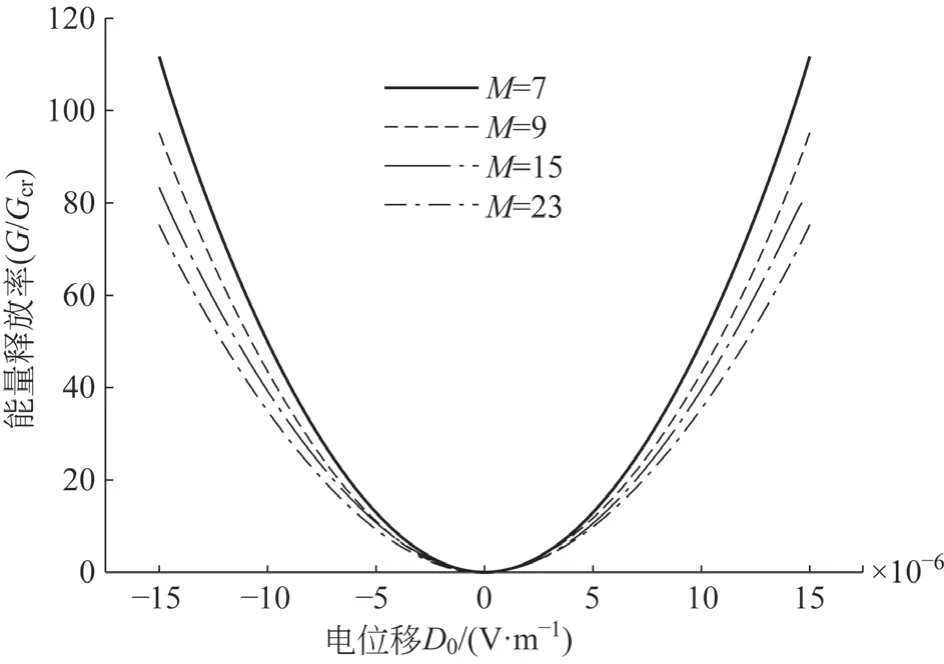
图9 反平面载荷为剪切应变时能量释放率G 与D0 的关系

由图8 可知，在第1 种加载情况下，能量释放率G与D0无关，与外加剪切载荷τ0有关,且τ0越大能量释放率越大；由式（37）可知k1(1)和k1(2)的大小与D0无关；由式（38）、式（39）可知，K1γ、K2γ仅与t1k1(1)、t2k1(2)有关，而与D0无关；结合式（37）～式（39）可得到能量释放率G与D0无关。由此，在第1 种加载情况下，能量释放率G只与外加剪切载荷τ0有关而与电位移D0无关；第2 种加载情况下能量释放率G与外加剪切应变γ0和电位移D0有关；G/Gcr总为正值，零点在外加电位移D0等于零的位置，与文献[16]结论一致，但与文献[17]的不同。文献[17]采用不可渗透条件，得出第1 种加载情况下的能量释放率G与D0有关，且可取负值。

5.2 弹性模量对能量释放率的影响

本文控制PZT-5H 的参数不变，对PZT-6B 的弹性模量进行改变，取PZT-6B 的弹性模量弹性分别为25 GPa、30 GPa、35 GPa、40 GPa、45 GPa、50 GPa、55 GPa、60 GPa、65 GPa，得到图10 所示能量释放率G随弹性模量的变化。由图10 可知，能量释放率G随材料弹性模量的增大而减小，且能量释放率减小的幅度降低，减小幅度由C44＝25×109N/m2时的1.2×10-9m2/N 变为C44＝65×109N/m2时的2.52×10-11m2/N，即材料弹性模量的增大能明显的阻碍裂纹扩展。

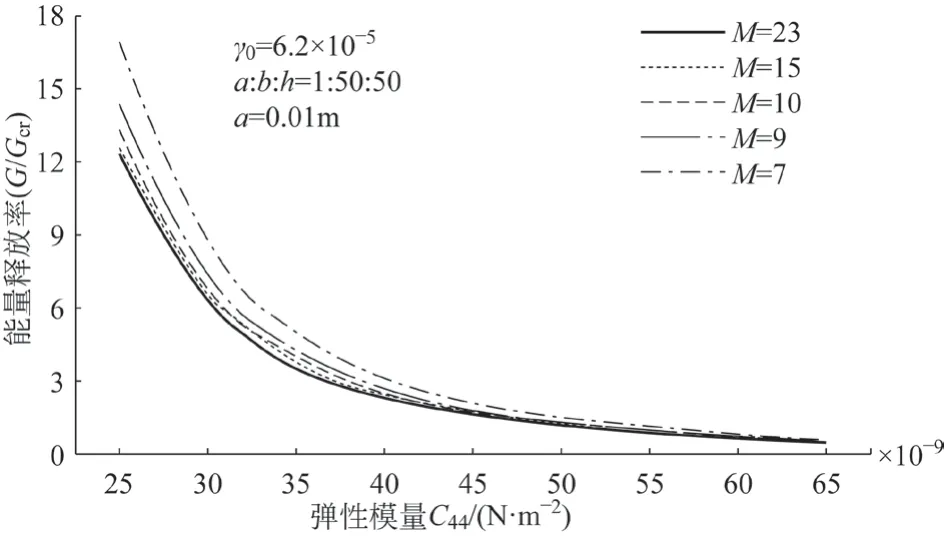
图10 材料弹性模量对能量释放率G 的影响

6 近年文献研究分析

表2 给出了2016 年～2022 年参考文献的研究内容对比，主要进行了载荷类型、材料类型和研究方法的对比。在裂纹形式上，本文与表中文献都不同，研究的是压电双材料的边裂纹扩展，表中文献均为中心裂纹，研究方法上采用了较有限元法更简单的边界配置法；载荷形式上，分析了2 种多场耦合下的压电双材料裂纹扩展，表中论文均只考虑了一种多场耦合条件下的压电双材料裂纹扩展。

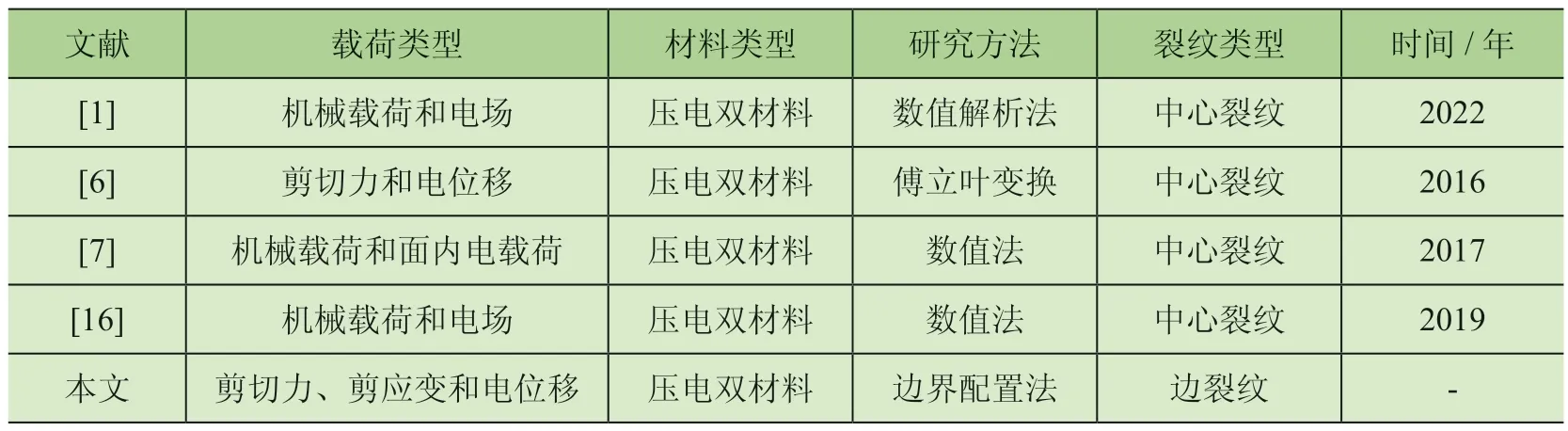
表2 近年文献研究内容对比

7 结论

1）在裂尖处，应力具有1/2 阶的奇异性；式(37)可看出介质Ⅰ、Ⅱ的应力强度因子是相同的。

2）应力强度因子的大小与材料的尺寸比有关，当材料长度b和材料厚度h不变时，应力强度因子随着裂纹长度a的增加而增加；当材料长度b和裂纹长度a不变时，应力强度因子随着材料厚度h的增加而减小。

3）在外加剪切载荷作用下，应力强度因子与外加电场的大小无关，能量释放率与外加电场的大小无关，但与外加剪切载荷τ0有关；而当外加剪切载荷变为剪切应变时，能量释放率与外加电场的大小有关，且总为正值，零点约在外加电位移为零处。

4）能量释放率还与材料的弹性模量有关，能量释放率随材料弹性模量的增大而减小，且能量释放率减小的幅度降低，即材料弹性模量的增大有明显的止裂作用。幂级数个数和边界配点数都对边界配置法的值有影响，当幂级数个数和边界配点数较少时边界配置法得出的值与真实值之间存在差距，但随着幂级数个数和边界配点的增加，边界配置法求出的值逐渐趋于稳定，更接近真实情况。