基于多过程模型融合的流化床配风解耦燃烧参数预测与优化

狄子琛,常成功,杨凤玲,吴海滨,程芳琴

(1.山西大学 资源与环境工程研究所,山西 太原 030006;2.清华大学 环境学院,北京 100084)

0 引 言

循环流化床(CFB)在过去20 a被广泛用于煤炭燃烧[1]。近年来,由于流化床的燃料适用性以及固废、垃圾、生物质等低品位燃料的热处理受广泛关注[2]。现流化床设备用于燃烧不同燃料时需进行适应性改造[3]。通常,鼓风量、一二次风口位置是需要调控的主要参数。准确模拟和预测不同工况下流化床炉内燃烧状况对其优化设计具有重要价值。

当前对流化床的模拟通常基于热力学平衡原理[4],将煤分解简化为元素组分,使用特定反应模块将其分解为挥发分和固定碳[5],然后采用RGibbs单元模型基于吉布斯自由能最小原理模拟燃烧过程。MOSHI等[6]利用该方法分别模拟了固定床气化炉和用于褐煤燃烧的CFB锅炉。PEI等[7]将此方法扩展到300 MW电厂的煤粉燃烧模拟过程,预测富氧燃烧条件下的烟气量和烟气组成。研究表明利用RGibbs模型模拟固体燃料燃烧和气化过程具有可行性。但该方法仍存在一定局限性,由于忽略了气固流体动力学和化学反应动力学,因此,其仅适用于模拟达到反应平衡的系统,只能用于预测反应最终产物。实际上,由于停留时间的限制,循环流化床内的燃烧反应不易达到热力学平衡。因此,如SOTUDEH-GHAREBAAGH 等[8]在模拟0.8 MW CFB研究中认为,气-固流体动力学和燃烧动力学对CFB模拟的准确性至关重要。

另一种方法基于试验数据,使用收率反应器RYIELD计算产物分布[9]。GUO等[10]开发了基于RYIELD模块的Aspen Plus仿真模型,对300 MW燃煤发电系统进行优化。产率由Chemkin反应动力学试验确定。该方法与试验结果吻合较好;然而,产品产率通常与操作条件密切相关,而流化床内反应条件变化剧烈,这为过程的准确模拟带来挑战。

为了更高效耦合动力学模型进行流化床预测,基于RCSTR模块的动力学模型广泛发展。LIU等[11]嵌入FORTRAN子程序模拟30 kW循环流化床燃烧室,评估了气固流体动力学和反应动力学对燃烧过程的影响。PETERS等[12]基于生物质组分热解动力学方程和化学反应方程建立了生物质动力学模型,并利用RCSTR模型模拟了反应温度和反应停留时间对燃料转化的影响。通过与实际运行的流化床进行比较表明,相比基于热力学平衡和试验结果的模拟方案而言,该方案具有更高的准确性。但该方法建模过程较复杂。

当前研究普遍基于单一过程模型进行流化床模拟。通常,基于热力学的模型过度简化,而基于动力学的模型则往往过于复杂,缺乏灵活性。事实上,不同流化床参数的主要影响因素存在显著差异。如需氧量通常由燃料中可燃组分含量和燃烧平衡态决定,此时基于热力学的模拟方法适合;而一、二次风位置与流化床内的解耦燃烧状态高度关联,需计算非平衡态下的锅炉运行状态,此时需采用动力学模型进行预测[13]。因此,联合多种建模方法进行流化床模拟,更有利于获取准确的流化床运行参数;同时,多模型协同可降低对单一模型的要求,从而为模型简化奠定基础。

基于此,针对当前流化床模拟模型难以兼顾多参数精准预测的问题,协同构建了基于热力学和动力学的300 MW流化床过程模型,可实现对需氧量、床层孔隙率、床层温度、气体分布等关键参数的灵活预测,指导鼓风量、一二次风口位置的设计和改造。

1 工艺设计

1.1 CFB燃烧器的燃煤过程

为便于与实际运行工况对比,选取煤矸石作为模拟对象。某煤电企业300 MW循环流化床燃烧室的结构示意如图1所示。本研究燃烧室的高14.703 m、宽15.051 m。在燃烧器尾部安装旋风分离器,用于分离烟气中的固体颗粒,而在旋风分离器的底部安装一个U型阀。煤粉自一次风气体分布板上方的给料口进入燃烧室。一次风被预热至200 ℃后进入燃烧室;二次风包含上二次风和下二次风,其中,下二次风位于分布板上方1.5 m处,上二次风高于下二次风4.09 m。相应地,锅炉被分割成不同的燃烧区域:一次风口至下二次风口为密相区,主要发生煤的干燥和热解;下二次风口以上为稀相区,其中下二次风口至上二次风口之间的区域主要发生挥发分燃烧,上二次风口以上发生焦炭燃烧[14]。

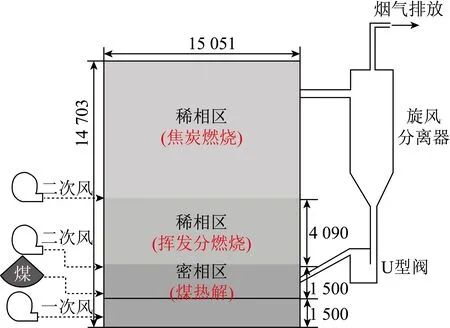
图1 300 MW循环流化床示意Fig.1 Schematic illustration of a 300 MW circulating fluidized bed

1.2 基于热力学方法的CFB燃烧室模拟

燃烧过程需氧量、气体产生量等参数可依据热力学平衡状态确定。基于热力学方法建立的Aspen Plus模型流程如图2所示。以煤矸石为例进行建模,原料来源于某煤矸石电厂。在模型中,煤矸石被定义为非常规成分,其组成基于元素分析确定,见表1。选取4种煤矸石进行分析,在较大的煤质变化范围内估计模拟结果的准确性。

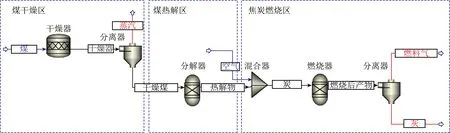
图2 基于热力学方法的循环流化床Aspen Plus过程模拟Fig.2 Aspen plus process simulation sheet of CFB based on thermodynamic method

表1 基于热力学分析的煤矸石化学成分Table 1 Chemical compositions of used coal gangue based on thermodynamics analysis %

嵌入FORTRAN子程序采用RSTOIC模块模拟干燥过程。HE等[15]研究中该反应可表示为mCOAL=0.055 508 4m(H2O),其中,mCOAL为煤的质量,m(H2O)为水的质量。水分和干燥煤通过SEP模块分离。干燥后的煤矸石进入RYIELD反应器简化表示为元素形式,将其分解为C、H、O、N、S和灰分等组分。在与二次风混合后,固体颗粒和挥发分在RGibbs模型中转化为气体产物和煤灰。根据吉布斯自由能最小原理,采用HCOALGEN模型和PR-BM函数分别计算了常规组分的物性和焓值。模拟模型所涉及的模块及参数见表2。主要假设如下:① 不考虑焦油;② 反应过程趋于热力学平衡状态。

表2 模拟模型涉及的模块及参数Table 2 Initial values of related parameters in each module for simulation

1.3 基于动力学模型的循环流化床燃烧室模拟

除需氧量、气体产生量等参数外,很多过程参数与非平衡条件下的燃烧状态有关,如床层空隙率、不同床层高度的气体分布等。这些参数直接决定锅炉解耦燃烧状态,对于调控一、二次风进风位置至关重要,而这些参数的确定依赖非平衡态下的锅炉运行状态,此时需采用动力学模型进行预测。基于动力学模型的模拟流程如图3所示。在该模型中,物性方法采用RK-SOAVE。将煤定义为非常规组分,采用COALGEN和DCOALIGT模型分别计算焓和密度。模拟矸石的化学组成见表3。为表征煤矸石转化过程中产生的半焦和灰分,基于试验确定半焦和灰分的工业分析和元素分析结果。

表3 基于动力学分析的燃料化学组成Table 3 Chemical compositions of bituminous coal based on kenitic analysis %

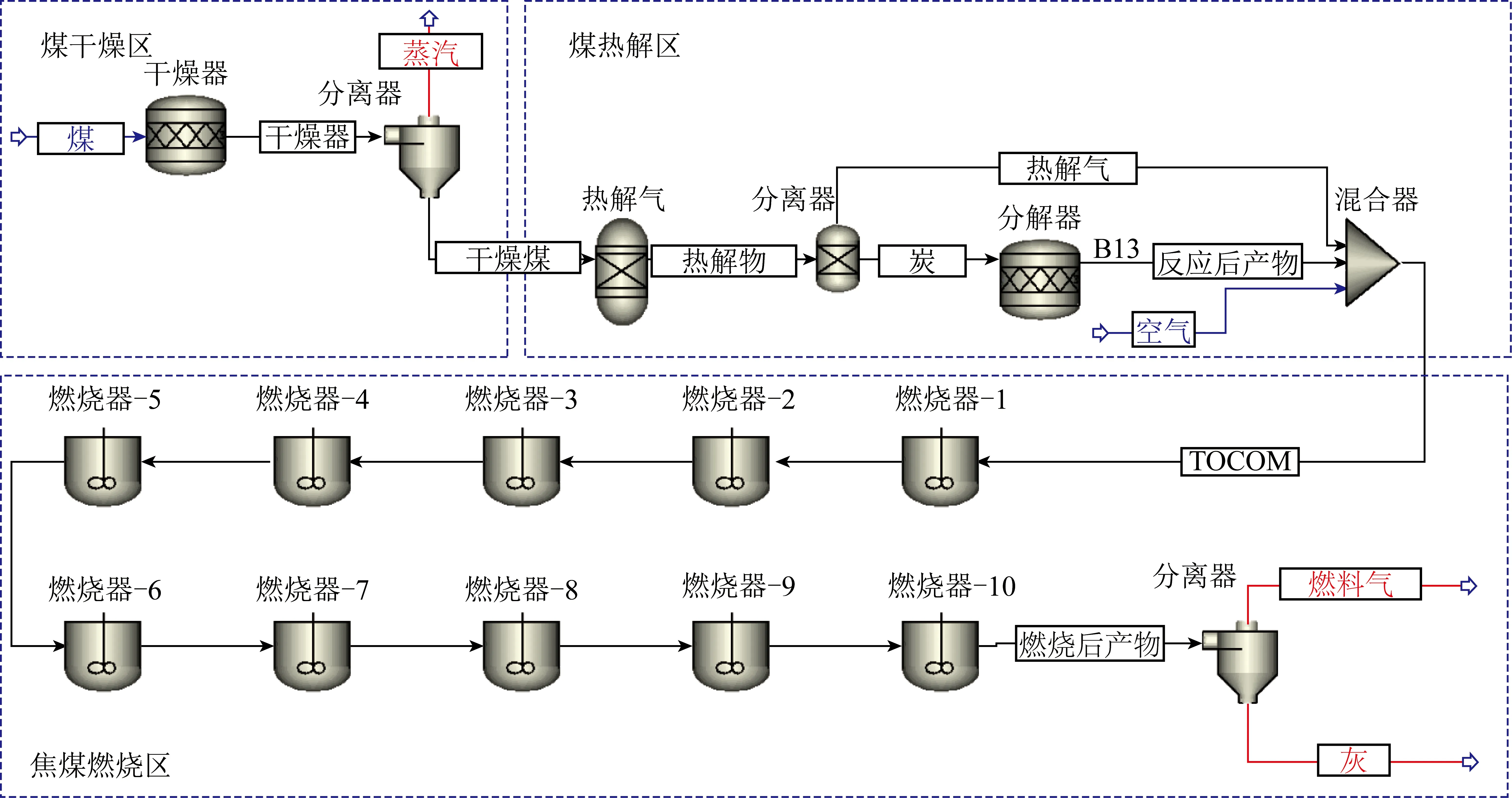
图3 基于动力学模型的循环流化床Aspen Plus过程仿真Fig.3 Aspen plus process simulation sheet of CFB based on kinetic model

当燃料沿燃烧室向上移动时,依次发生干燥、热解、挥发分燃烧和焦炭燃烧。各模块相关参数的作用及初始值见表4。在干燥(DRIER)和分解(DECOMP)模块中,与热力学模拟模块相似。热解过程中,煤被分解为挥发分、焦炭和焦油(C6H6),其中挥发分由CO、H2、CO2、H2O、H2S、N2、CH4组成。根据热解反应试验结果确定各热解产物和产量。需特别指出的是,试验未考虑含N、S物质的排放,这部分工作将在后续工作中进行详细研究。为确保模拟热解产物燃烧过程的准确性,本研究通过嵌入的FORTRAN子程序提出了动力学模型[16-17]见表5。利用连续的RCSTR模型分别计算挥发分和焦炭的燃烧过程。每个RCSTR模型体积相同,即整个燃烧室容积/串联的RCSTR数量。

表4 模型涉及的模块及参数Table 4 Initial values of related parameters in each module for simulation

表5 燃烧阶段反应动力学方程Table 5 Chemical reaction kinetic equation for describing combustion of pyrolysis products

2 结果与讨论

循环流化床锅炉的设计和优化需确定需氧量、一次风和二次风分布等关键参数。具体而言,需氧量主要由燃料类型决定,可用热力学方法计算。然而,确定一次风和二次风的分布可能相对复杂,与燃烧状态以及床层高度密切相关,需建立燃烧动力学模型。为便于实际应用,笔者建立了热力学和动力学相结合的煤燃烧过程的简化模型,初步计算需氧量随燃料变化的曲线以及空隙率和温度沿床层高度变化的曲线。

2.1 不同燃料燃烧的需氧量预测

与试验或直接测量相比,模拟是确定不同煤种需氧量更有效的方法,模拟结果如图4所示。研究采用CO和CO2的流量反映完全燃烧程度。在整个燃烧过程中,不同种类的煤矸石随供氧量增加而呈现规律基本一致,即氧气不足时,一部分煤被氧化为CO,随氧气持续供应,燃烧继续进行,最终全部转化为CO2。因此,在氧气过剩时,CO流速为0,所需的最小供氧量与理论需氧量相同。据此推算,4种煤完全燃烧的需氧量分别为15.17、4.00、4.47、6.20 kg/h,这主要与表3的煤种碳含量有关。因此,可相对准确建立煤种与理论需氧量之间的关系,从而帮助设计风机功率、风量等相关参数。

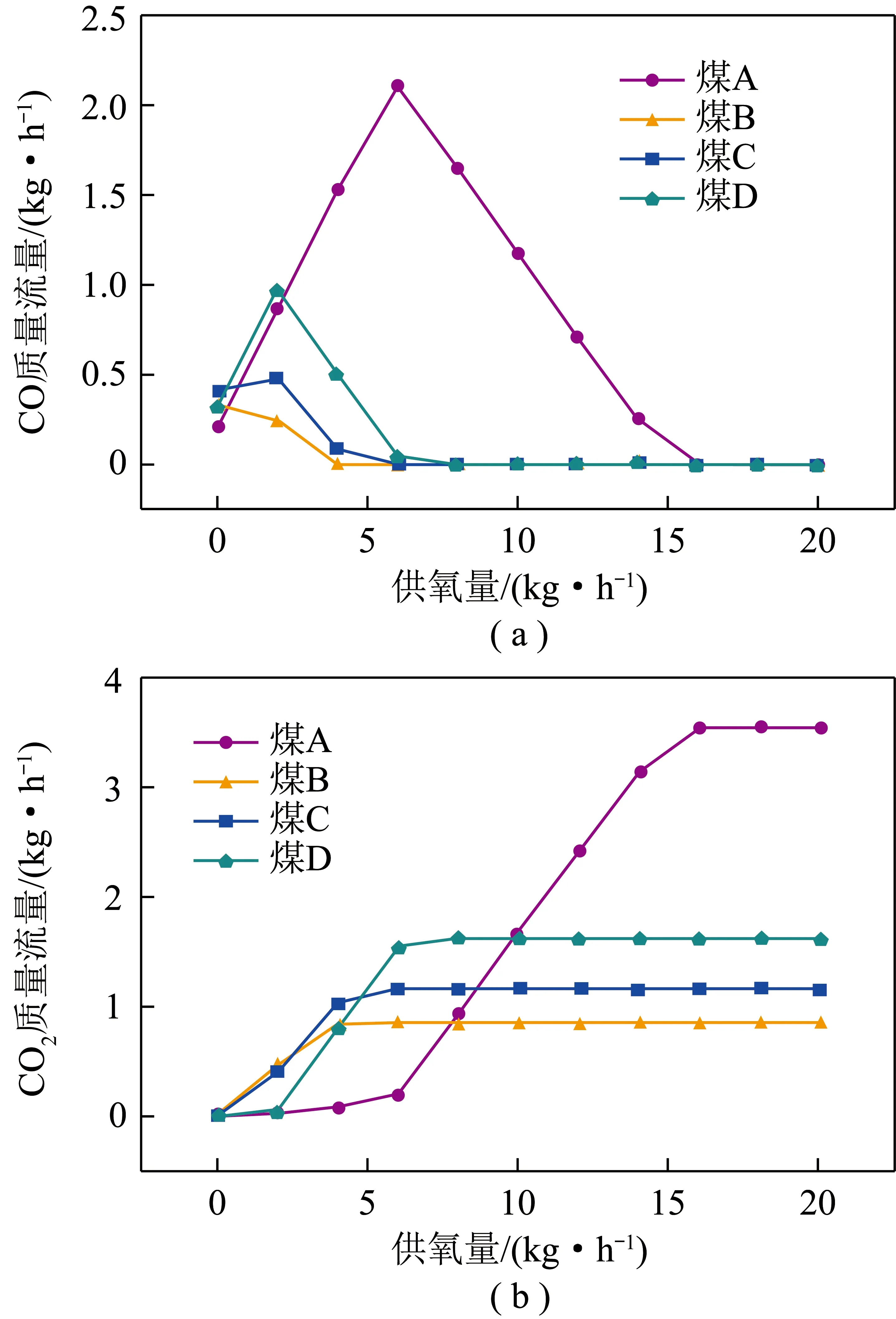
图4 供氧量对碳流量的影响Fig.4 Effect of oxygen supply on carbon flow rate

2.2 床层空隙率对碳流量的影响

床层空隙率对碳流量的影响如图5所示,采用10个串联的RCSTR模型对2种情况进行研究,一种情况是将床层空隙率恒定保持在0.4,另一种是将床层空隙率由0.4逐渐增至0.7。当CFB的空隙率为0.4时,随床层高度由0增至14.703 m,碳流量由3.23 kg/s降至0。当设置床层空隙率在0.4 ～ 0.7呈线性增加,碳流量速率下降较慢。这是因为增加床层空隙率导致反应器单位体积的颗粒数量减少,进而降低反应器的碳消耗率,最终导致更高的碳含量流量[18]。可知设置床层空隙率的精准性对模拟结果有一定影响。KRISHNUDU等[19]通过试验证实床层空隙率呈线性变化。因此,在本模型中采用第2种情况下的床层空隙率设置。

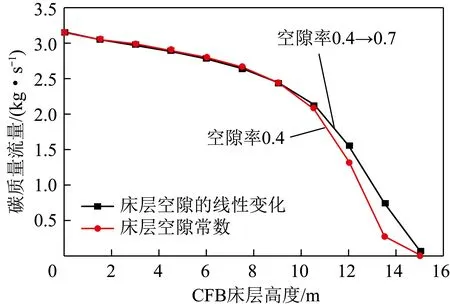
图5 床层空隙率对碳流量的影响Fig.5 Effect of bed voidage on carbon flow rate

2.3 CFB温度随床层高度的变化

循环流化床温度随床层高度的变化情况如图6所示。床层高度由底部增至3.0 m过程中,温度迅速升高,最大值达1 081 ℃。继续增加CFB高度,温度开始逐渐降低,最终维持在885 ℃左右。这是由于密相区氧气不足,温度最初较低。当煤进入稀相区时,二次风迅速提供燃烧所需的氧气。此时,热解阶段产生的挥发分与新供给的氧气迅速反应。因为是放热反应且反应速率较快,故温度迅速上升。煤继续向锅炉顶部移动,此时主要是未燃烧的焦炭在燃烧。由于焦炭燃烧相对缓慢,加上床层空隙率增加,温度开始逐渐下降并趋于稳定。这些结果与LIU等[20]的模拟结果和JI等[21]的CFB实际运行数据吻合程度较好,因此说明所建立的模型能够较准确模拟锅炉温度状态。

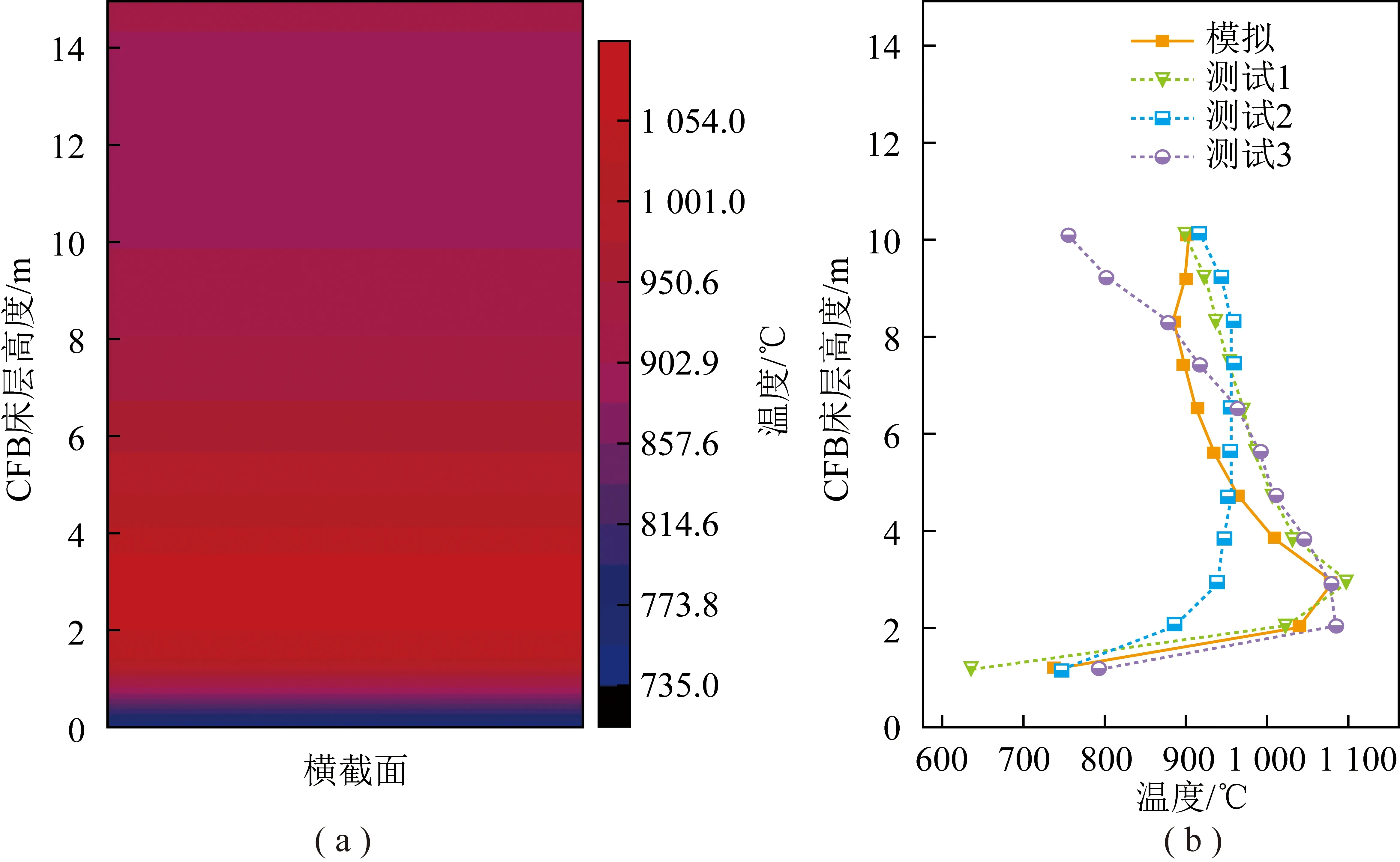
图6 温度随床层高度的变化Fig.6 Profile of temperature along with the height of the bed

2.4 CO和CO2摩尔分数随床层高度的变化

CO和CO2摩尔分数随床层高度的变化如图7所示。随CFB高度增加,CO的摩尔分数先上升至0.13 mol/mol,然后逐渐下降至0.08 mol/mol,这与温度随高度增加的变化趋势相似,说明燃烧气氛的分布与煤在锅炉内的解耦燃烧过程密切相关。在整个燃烧过程中,CO2摩尔分数从锅炉底部向锅炉顶部单调增长,上升速率初始升高较慢,随后快速上升。

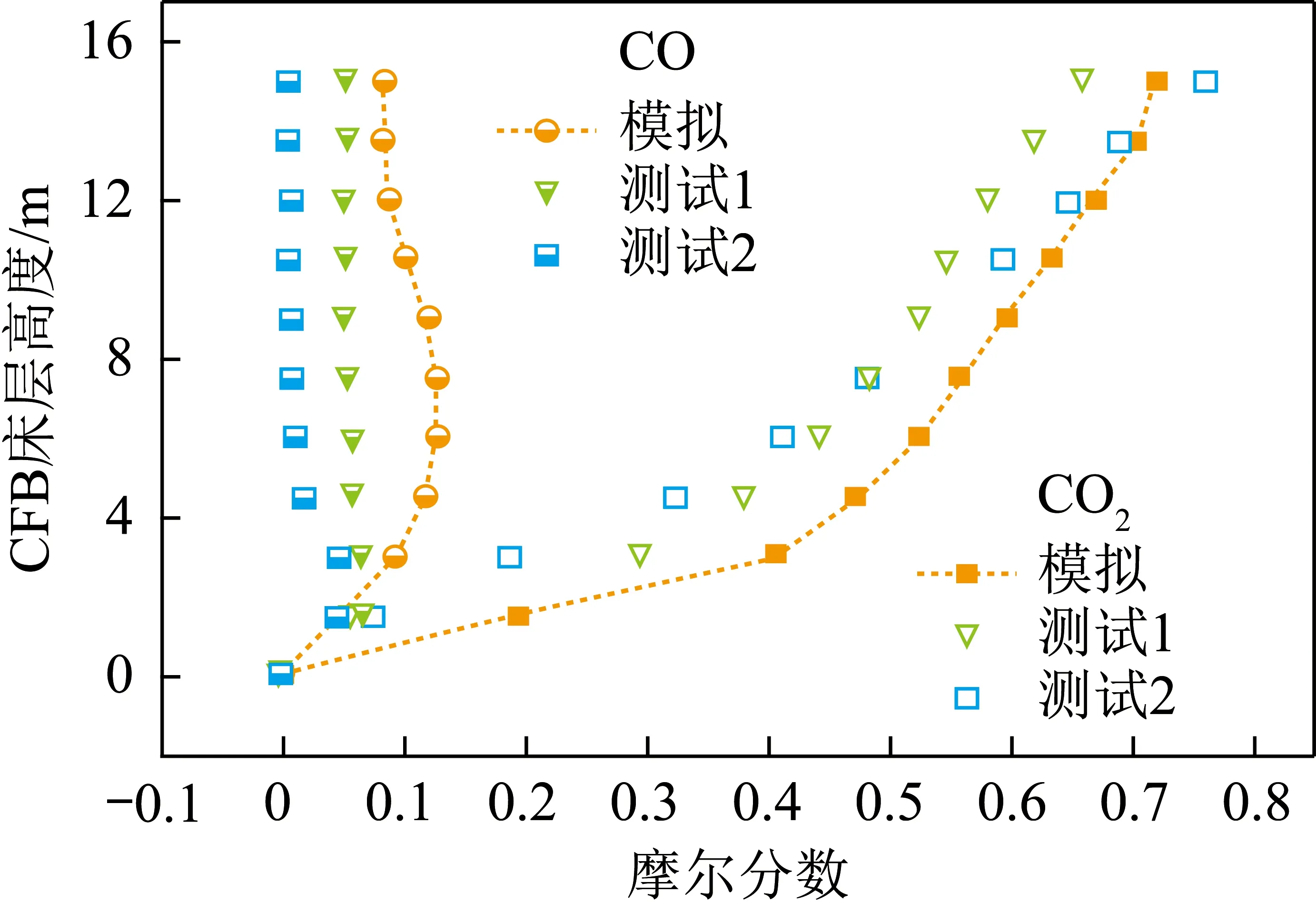
图7 CO和CO2摩尔分数随床层高度的变化Fig.7 Mole fraction of CO and CO2 along with the height of the bed

这是由于在锅炉底部的初始流化阶段,床层孔隙率较低,且空气供应不足,此时主要表现为不完全燃烧,这一阶段煤主要进行热解,碳没有完全氧化[21],因而CO2上升趋势最初较缓慢。随二次风引入,有足够的氧气完全燃烧CO和焦炭。模拟结果与锅炉试验[22]趋势一致性较好,计算结果可靠。

上述结果表明,所建立的模型能较好模拟煤从锅炉底部向锅炉顶部移动的燃烧过程,可为设计一次和二次出风口位置分布提供参考。

3 结 论

1) 构建基于热力学的过程模型,准确预测了4种煤矸石的理论需氧量。当燃料碳含量为74.05%、17.71%、24.27%、34.01%时,理论需氧量分别为15.17、4.00、4.47、6.20 kg/h。计算结果较准确建立了煤种与理论需氧量的关系,帮助设计风机功率、风量等相关参数。

2) 在此基础上,通过串联10个RCSTR动力学模块,并嵌入FORTRAN动力学子程序,实现不同床层空隙率、床层温度、气体分布等关键参数计算。模拟结果表明,床层空隙率对碳流量影响较大。空隙率设置为0.4时,随床层高度由0增至14.703 m,碳流量由3.23 g/s降至0;设置床层空隙率在0.4～0.7线性增加时,碳流量速率下降较慢,反映温度、气体分布随床层高度变化更准确。

3) 温度和气氛分布与氧含量和解耦燃烧过程密切相关。通过本研究构建的模型可实现趋势准确预测,单点参数误差低于15%,可有效指导燃料变换时一、二次风进风位置和进风量调节。