小周期结构磁-力-电耦合问题的高阶双尺度渐近分析
2023-09-01刘宇铭冯永平
刘宇铭,冯永平
(广州大学 数学与信息科学学院,广东 广州 510006)
0 引 言
磁-力-电耦合行为普遍存在于压磁材料、压电材料以及人工智能材料中,在多物理场作用下,新材料就会表现出复合材料特有的磁-力-电耦合效应。这些磁-力-电耦合材料已经在航天、人工智能等领域中得到了广泛的应用。早期已有很多学者对相关材料属性进行了研究,Suchtelen[1]研究发现压磁与压电复合材料中会产生磁电耦合行为;Qing等[2]得到了三维磁-力-电耦合问题的Hellinger-Reissner变分原理;Lee[3]和He[4]先后分别构造了一些不同的泛函变分描述热-磁-力-电耦合行为。对于求解耦合问题的解中,Pan等[5-6]、Jiang等[7]得到了多层功能梯度矩形板和含二维多边形夹杂的各向异性磁-电耦合的解析解。磁-力-电复合材料在宏观结构上有非绝对均匀性,对磁-力-电耦合问题进行多尺度分析具有重要的理论意义及应用前景。本文将用高阶双尺度方法分析满足第一类边界条件的小周期结构中磁-力-电耦合问题的渐近行为及均匀化行为。
现在,用双尺度方法解决耦合问题已经越来越广泛。文献[8]中用新型的高阶多尺度渐近法分析了具有周期孔洞结构的复合材料问题,给出相应的均匀化方程和均匀化常数以及有限元算法;文献[9]中对复合材料用有限元方法进行数值计算时计算量庞大,在已有的双尺度分析与有限元分析的基础上,给出了构建边界层和周期单胞的双尺度有限元计算方法;文献[10]构建了新型双尺度有限元方法,利用匹配边界层分析,得到位移和电势的相互耦合关系,最后分析其双尺度有限元解的渐近估计误差,并通过数值计算检验其方法的有效性;文献[11]在构造的边界层上,运用多尺度有限元方法解决复合材料中具有周期震荡系数的热传导问题,并给出其多尺度截断误差估计,且用三维数值案例验证其算法的正确性与有效性;文献[12]通过构造带有周期阻尼结构耦合问题的L-阶双尺度渐近解,运用双尺度展开方法求解,最后得到其L-阶双尺度有限元解的渐近误差估计。
数学上,第一类边界条件下小周期性区域中的磁-力-电耦合问题可用以下偏微分方程组的边值问题来表述[13]:
(1)
其中:
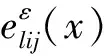
(ⅱ)Ω是有界的小周期闭区域且满足Lipschitz边界条件;

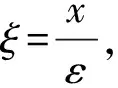

cijkl(ξ)是有界可测函数
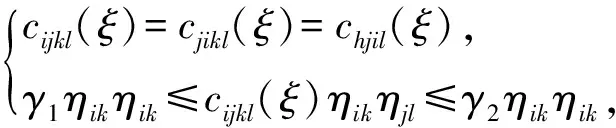
其中,{η}为任意实对称矩阵,γ1,γ2是与ε无关且大于 0 的常数。
类似地,κil(ξ)是有界可测函数:
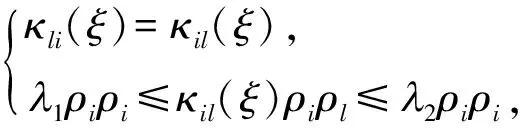
其中,{ρ}为任意实对称向量,λ1,λ2是与ε无关且大于 0 的常数。
考虑如下偏微分方程组:

(2)
其中,Fj(ξ),Uj(ξ),j=0,1,2,…,是关于ξ为1-周期的向量函数或标量函数,且Fj(ξ),Uj(ξ),∈L2(Q),W=(W1,W2,…,Wn)T,Q为小周期单胞。
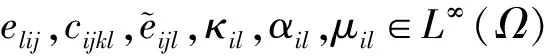
1 uε(x),ψε(x),φε(x)双尺度形式渐近展开式
假设uε(x),ψε(x),φε(x)具有如下的渐近展开形式:
(3)
(4)
(5)
其中,Mα(ξ),Nα(ξ),Pα(ξ),Eα(ξ),Rα(ξ),Sα(ξ),Tα(ξ),Fα(ξ),Gα(ξ)为周期单胞Q上待定的周期单胞函数;Mα(ξ)为待定的函数矩阵;Nα(ξ),Pα(ξ),Eα(ξ),Rα(ξ)为待定的向量函数;Sα(ξ),Tα(ξ),Fα(ξ),Gα(ξ)为待定的标量函数;u0(x),ψ0(x),φ0(x)为待定的均匀化解。
将方程(3)、(4)、(5)代入方程组(1)并通过整理合并,对比等式两端ε-1同次幂的系数,可得到以下求解待定单胞函数组的3个方程组:
(6)
(7)
(8)
对比等式两端ε0同次幂的系数,并在Q上作关于ξ积分,得到以下形式等式:
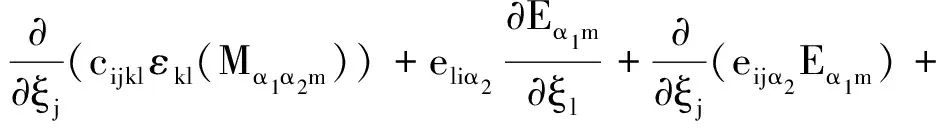
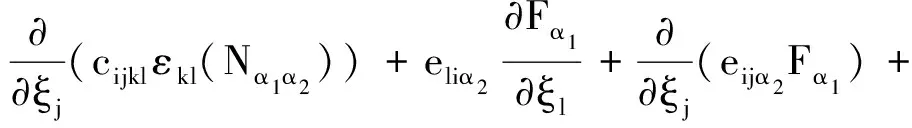
fi(x), inΩ;
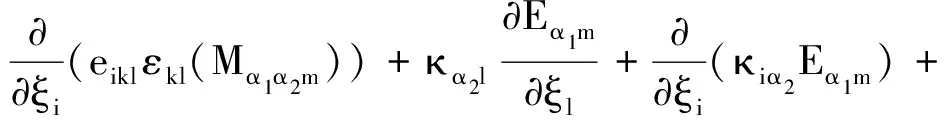
inΩ;

inΩ。
由以上3式,问题(1)的均匀化解组(u0(x),ψ0(x),φ0(x))可由以下均匀化方程组定解:
(9)
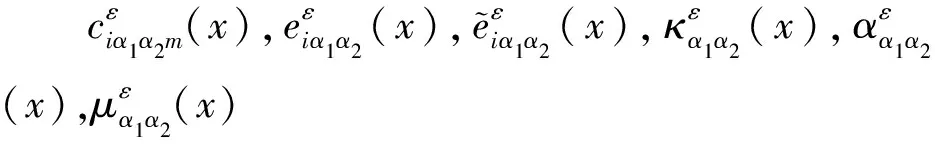
(10-1)
(10-2)
(10-3)
(10-4)
(10-5)
(10-6)
而(Mα1α2m,Eα1α2m,Rα1α2m),(Nα1α2,Fα1α2,Sα1α2),(Pα1α2,Gα1α2,Tα1α2),可分别在Q上由以下方程组定解。

(11)

(12)
(13)
当l≥2时,通过比较方程两端ε1,ε2,ε3,…,所有待定单胞函数可以类似递推定解。
注2:由 Korn 不等式及 Lax-Milgram 引理易证方程组(6)、(7)、(8)、(9)、(11)、(12)及(13)在相应函数空间中存在唯一弱解组。
定理1若be(x),bm(x),fi(x),u0(x),φ0(x),ψ0(x)在Ω内足够光滑,则
(ⅰ)方程组(1)有(3)、(4)、(5)的渐近展开形式;
(ⅳ)均匀化解u0(x),ψ0(x),φ0(x),由方程组(9)定解;
2 双尺度渐近解误差估计
在实际的数值计算中,通常用二阶双尺度近似解计算解组(uε(x),ψε(x),φε(x)):
(14)
(15)
(16)
定理2 设(uε(x),ψε(x),φε(x))为方程组(1)的弱解组,设fi(x)∈H2(Ω),be(x)∈H2(Ω),bm(x)∈H2(Ω),u0(x)∈H4(Ω),φ0(x)∈H4(Ω),ψ0(x)∈H4(Ω),则有如下渐近估计:
其中,C1,C2,C3是与fi(x),be(x),bm(x),u0(x),φ0(x),ψ0(x)无关的正常数。
注3:在一般区域中,磁-力-电耦合材料的等效性能可用匹配的边界层问题展开相关问题研究。
注4:本文利用边界值为0的第一类边界条件定义周期单胞函数,在实际问题中,当对材料问题做适当对称性假设后可使用周期性边界条件定解单胞函数,并且可证明这两种定义方式定解是同一个唯一解。
3 小 结
本文通过双尺度方法分析了第一类边界条件小周期区域内磁-力-电耦合问题的高阶双尺度渐近解,并得到了其均匀化常数与均匀化解,最后证明了其二阶双尺度解的渐近误差估计。文中的双尺度方法对求类似问题的渐近解提供了可行的算法,也为进一步求数值解提供了理论基础。
