水库群长期优化调度时空组合降维算法
2023-09-01章汉军
陈 佳,章汉军,徐 囡
(1.诸暨市水利局,浙江 绍兴 311800;2.绍兴市柯桥区浙光中学,浙江 绍兴 312025)
动态规划(DP)是解决多阶段决策问题的经典方法,在水库调度领域获得了广泛应用[1-3]。受“维数灾”[4]限制,在当前计算能力下,DP难以直接应用于3个水库以上规模水库群联合优化。为了缓解DP的“维数灾”效应,研究人员提出了一系列降维技术,这些技术分为以提高计算效率为目的的并行计算技术[5-6]和以减少计算工作量为目的的改进型DP[7-10]2类。并行计算的优势在于能够提高计算资源使用率,尤其是有助于发掘多核处理器的计算潜能。但是,并行计算的本质是以空间资源换取时间,因计算工作量并未减少,随着问题规模增大,DP的计算成本仍然难以承受。改进型DP主要从4个方面减少DP计算工作量。①利用实际问题的数学特性减少计算工作量。如赵铜铁钢等[1]基于水库状态变量与决策变量之间的单调关系,提出2种DP改进型,避免了冗余计算;ZENG等[11]利用时段初并联水库系统总可用水量与时段末水库最优蓄水量之间的单调关系,对DP进行改进,精简了DP计算过程。②通过规避重复计算或者无效计算减少计算工作量。如纪昌明等[2]通过构建水电站出力泛函模型,精简了DP计算步骤,提高了计算效率;纪昌明等[12]通过构建可行域搜索映射模型,规避了无效状态组合计算,缩减了DP计算时间。③采用抽样技术减少计算工作量。如冯仲恺等[13]使用试验设计表在水库状态空间中进行抽样,避免了水库全状态组合引起的“维数”问题;HE等[14]将重要性采样技术应用于梯级水库蓄水调度,缓解了DP“维数灾”效应。④对解空间进行分解,采用逐次逼近策略减少计算工作量。此类算法以离散微分动态规划(DDDP)[7]、动态规划逐次逼近(DPSA)[8]和逐步优化算法(POA)[9]为代表。DDDP将大范围的解空间分解为一连串重叠的小范围子空间,每次在1个子空间内应用DP寻优,并利用子空间的重叠性不断向相邻子空间渗透,进而实现对整个解空间的探索。DPSA和POA采用变量解耦策略,将高维解空间分解为若干低维子空间,通过在不同子空间内轮流搜索,逼近问题的解。
DPSA是一种“空间降维”方法。该方法首先通过对变量实施解耦,将水库群优化问题分解为一系列单库优化问题;然后自上而下进行逐库优化(每次仅对1座水库的蓄水轨线进行优化,同时固定其余水库的蓄水轨线);最后通过迭代,收敛于问题的解。DPSA最大的优势在于其计算工作量随水库数量呈线性增长,有效缓解了DP的“维数”问题。但是,DPSA的变量解耦策略难以有效处理梯级水库之间复杂的水力耦合关系。在梯级水库系统中,上、下游水库之间存在强水力耦合关系,这一关系增加了梯级水库联合优化问题的复杂性,主要体现在:①上游水库的放水构成下游水库入流的一部分,下游水库最优蓄泄方案由上游水库的蓄泄方案确定;②下游水库的蓄泄方案又反过来作用于上游水库的决策空间,影响上游水库的最优蓄泄方案。由于上述耦合关系的存在,在梯级水库联合优化中采用DPSA变量解耦策略,当搜索至约束边界上时容易出现“停滞不前”问题,影响解的质量。有关该问题的详细论证见下一节“1算法实证分析”。
POA是一种“时间降维”方法。该方法采用静态变量解耦策略,将多阶段问题分解为若干两阶段问题,通过连续、重复地求解两阶段问题,逼近多阶段问题的解。已有文献证明,对于凸问题,POA能够收敛于全局最优解。但是,实际水库优化问题往往具有“非凸”特征,对于“非凸”问题,POA的降维是以牺牲解的质量作为代价。总的来说,POA有2个方面的局限性:①搜索的盲目性影响解的质量,算法仅在少量固定的子空间中轮流搜索,不对变量进行比较、评价;②“维数”问题影响求解效率。POA两阶段问题计算工作量随水库数量呈指数增长,存在“维数障碍”[15]。为了提升POA的性能,研究人员提出了一系列POA改进型。这些改进主要围绕上述2个方面展开。围绕第1方面的改进主要有:廖胜利等[16]针对POA搜索至约束边界上易陷入局部最优解问题,提出了一种沿目标函数等值线向可行域内部移动的策略;CHENG等[17]设计了一种多步POA,通过多次应用POA对4、8、16、96个时段的水库群优化问题进行求解(当前问题的最优解作为下一问题的初始解),提高了POA解的质量;黄草等[18]引入“优化窗口”和“滑动距离”概念,将POA两阶段优化和单步移动扩展为多阶段优化和多步移动;肖胜贤等[19]针对坐标轮换法求解POA两阶段问题搜索至约束边界上“停滞不前”问题,提出了一种等约束滑行策略;张诚等[20]在文献[18]的基础上设计了一种变阶段POA,将POA两阶段模式拓展到多阶段模式;JI等[21]考虑河道水流传播对梯级水库短期调度的影响,对POA两阶段效益函数进行改进,设计了一种嵌套POA。围绕第2方面的改进主要有:MA等[22]采用智能算法求解POA两阶段问题,避免了水库全状态组合引起的“维数”问题;李义等[23]采用坐标轮换法求解POA两阶段问题,减少了POA一次寻优的变量数;胡挺等[24]将DDDP“廊道”技术引进POA两阶段问题求解,减少了POA一次寻优的状态数;冯仲恺等[25]将试验设计引进POA两阶段问题求解,缓解了POA“维数”问题;赵志鹏等[26]采用离散梯度下降法求解POA两阶段问题,减少了POA计算工作量;FENG等[15]采用Nelder-Mead单纯形方法求解POA两阶段问题,减轻了POA计算负担。此外,CHEN[27]针对POA相邻时段水量分配机制的不足,对POA两阶段效益函数进行改进,设计了一种跨时段水量分配机制,并采用DP求解两阶段问题,提高了POA解的质量和求解效率。虽然通过不同的改进措施,POA的性能得到了一定程度的提升,但是,现有改进措施均未能从根本上解决POA“盲目搜索”问题和“维数”问题。
为了进一步提高水库群调度问题的求解质量和效率,本文一方面综合DPSA和POA的降维优势,另一方面针对2种算法的不足进行改进,设计一种时、空组合降维技术,并将其命名为IPOA-CBSA(Improved POA with Chain-Based Successive Approximation)。IPOA-CBSA采用CBSA框架,将复杂水库网络分解为若干“梯级水库链”子网,然后轮流对各“梯级水库链”子网进行优化,直至收敛。其中,各“梯级水库链”子网问题采用IPOA进行求解。CBSA是DPSA变量解耦策略的改进型,将DPSA“单库轮流”优化模式拓展至“梯级水库链轮流”优化模式,通过对各“梯级水库链”子网进行整体优化,更好地处理梯级系统内部水力耦合关系。IPOA采用动态变量解耦策略(Dynamic Variable Decoupling Strategy,DVDS)进行降维,弥补POA静态变量解耦策略搜索的盲目性,改善解的质量;同时引进扰动机制,缓解POA两阶段问题求解的“维数”问题。本文试图通过对2种经典算法进行改进和综合,提高大规模复杂水库群优化问题的求解效能。
1 算法实证分析
1.1 “两水库三阶段”问题
1.1.1目标函数
调度对象为A(上)、B(下)2座梯级水库。调度期为1年,划分为3个时段。调度问题可以简单描述为:在满足A、B水库各项物理、运行约束条件下,寻求2座水库的最优蓄泄方案,使得梯级系统调度期内总效益最大化。假设目标函数可以表示为max{2RA,1+4RA,2+3RA,3+3RB,1+4RB,2+2RB,3}。其中:RA,t、RB,t分别为A、B水库第t个时段的下泄水量(t=1,2,3)。
1.1.2约束条件
水库水量平衡方程:VA,t=VA,t-1+2-RA,t,VB,t=VB,t-1+RA,t-RB,t。
水库蓄水量上、下限:0≤VA,t≤3,0≤VB,t≤3。
水库下泄水量上、下限:0≤RA,t≤5,0≤RB,t≤5。
边界条件:VA,0=1,VA,3=1;VB,0=1,VB,3=1。
式中VA,t、VB,t——A、B水库第t个时段末的蓄水量。
对于上述问题,容易求得最优解相应的梯级系统蓄水轨线为:AV~(1,3,0,1),BV~(1,0,0,1),下泄轨线为:AR~(0,5,1),BR~(1,5,0),目标函数值为46。现给定初始解,分别采用DPSA和POA求解上述问题。初始解相应的梯级系统蓄水轨线为:AV~(1,3,1,1),BV~(1,1,0,1),下泄轨线为:AR~(0,4,2),BR~(0,5,1),目标函数值为44。
1.2 DPSA求解过程分析
采用DPSA进行求解,先考虑固定B水库蓄水轨线,对A水库蓄水轨线进行优化的情况。比较A水库初始下泄轨线AR~(0,4,2)和最优下泄轨线AR~(0,5,1)可知,要想获得最优下泄轨线,只需在初始下泄轨线的基础上,将1个单位的水量从第3个时段转移至第2个时段即可。按此操作后,B水库下泄轨线变为BR~(0,6,0),可知B水库第2个时段的下泄水量已突破上限约束。因此,可以判定上述操作不可行。再考虑固定A水库蓄水轨线,对B水库蓄水轨线进行优化的情况。比较B水库初始下泄轨线BR~(0,5,1)和最优下泄轨线BR~(1,5,0)可知,要想获得最优下泄轨线,只需在初始下泄轨线的基础上,将1个单位的水量从第3个时段转移至第1个时段即可。按此操作后,B水库蓄水轨线变为BV~(1,0,-1,1),可知B水库第2个时段末的蓄水量已突破下限约束。因此,可以判定上述操作亦不可行。由于2种情况下水库蓄水轨线均得不到改善,DPSA收敛于初始解。
此例说明:采用DPSA变量解耦策略难以有效处理梯级水库之间复杂的水力耦合关系。实际上,要想获得最优解,必须同时对A、B水库的蓄水轨线进行优化。
1.3 POA求解过程分析
采用POA进行求解,首先对初始解相应的梯级系统第2个时段末的蓄水状态进行优化,优化后梯级系统蓄水轨线变为AV~(1,3,0,1),BV~(1,1,1,1),下泄轨线变为AR~(0,5,1),BR~(0,5,1),目标函数值变为45。此后,在POA优化机制下,梯级系统蓄水轨线再也得不到改善,算法收敛。比较POA收敛解与最优解可知,要想获得最优解,只需在收敛解的基础上,将B水库1个单位的水量从第3个时段转移至第1个时段即可,由于B水库第2个时段的下泄水量已达上限值,可以判定,在POA优化机制下,上述跨时段操作无法实现。
此例说明:POA仅在T-1个固定子空间中搜索,无法保证收敛于最优解,其中,T为调度期时段总数。实际上,要想获得最优解,必须为POA提供更多的搜索空间。
2 IPOA-CBSA
2.1 CBSA
考虑M座水库联合优化问题。DPSA采用变量解耦策略,将M座水库联合优化问题分解为M个单库优化问题,缓解了DP的“维数灾”效应。但是,这种缓解是以牺牲解的质量作为代价的。DPSA最大的缺陷在于其“单库轮流”优化模式难以有效处理梯级水库之间复杂的水力耦合关系。DPSA时间复杂度和空间复杂度分别为O(M·T·K2)和O(T·K),K为水库状态离散点数。更多DPSA详情参见文献[8]。
为了弥补上述缺陷,本文考虑以“梯级水库链”为优化单元,将DPSA“单库轮流”优化模式拓展至“梯级水库链轮流”优化模式。以图1所示“十水库”系统为例,阐述CBSA的优化过程。首先,采用常规方法(如等流量法)获得“十水库”系统各水库初始下泄轨线;然后,将“十水库”系统分解为1-7-10、2-4-7-10、3-4-7-10、5-7-10、6-7-10和8-9-10共6个梯级水库链;最后,轮流对6个梯级水库链的下泄轨线进行优化,直至收敛。具体步骤如下。
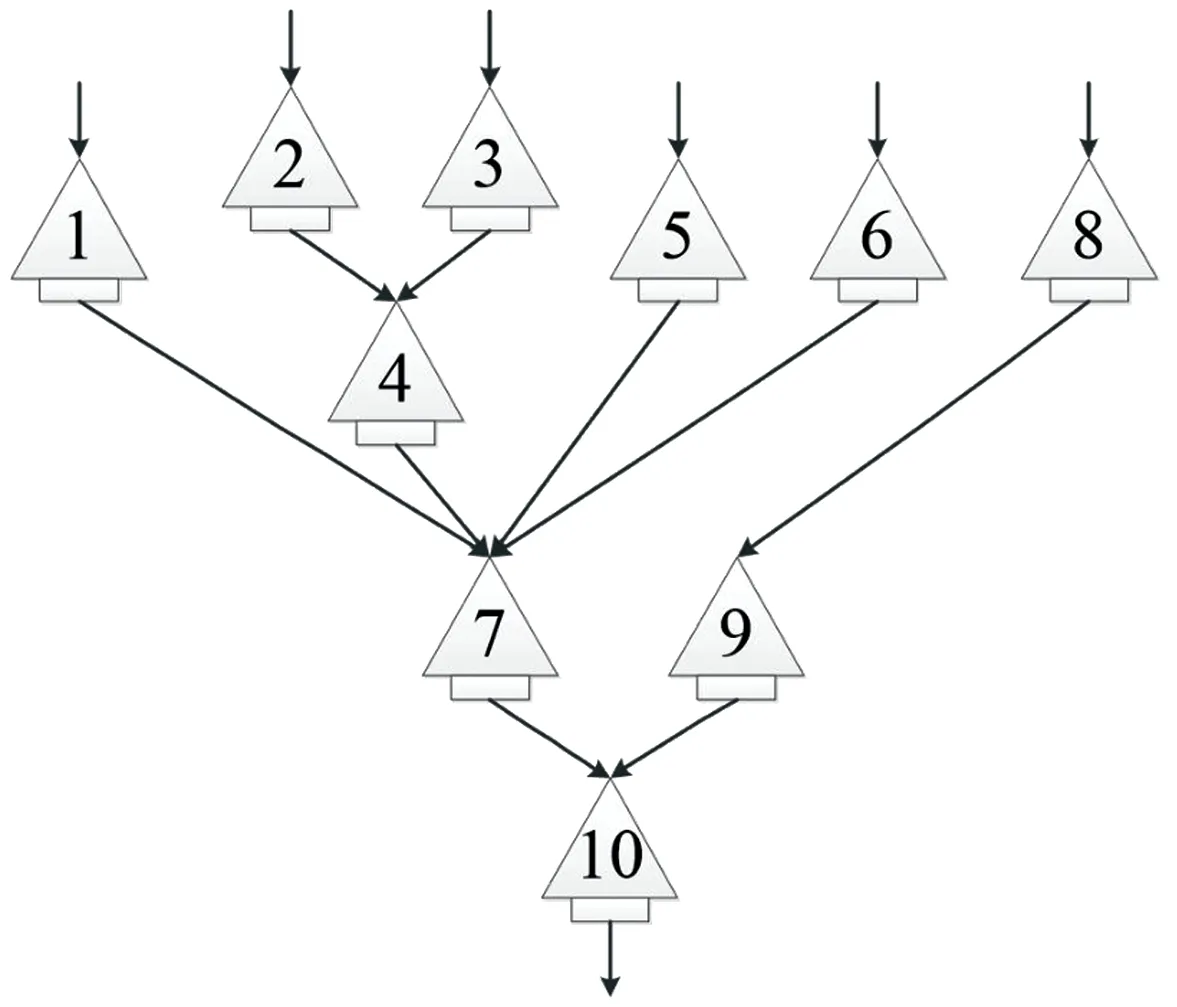
图1 “十水库”系统结构
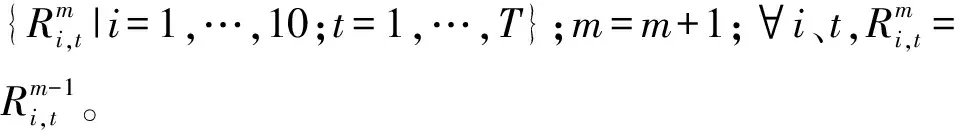
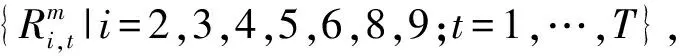
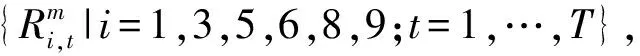

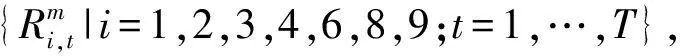

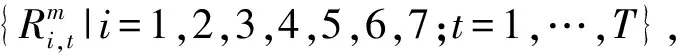
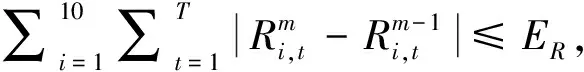
对于M座水库T个时段的优化问题,假设水库群系统包含n个梯级水库链,则CBSA优化步骤如下。

步骤二固定第j个梯级水库链以外各水库的下泄轨线,采用IPOA对第j个梯级水库链以内各水库的下泄轨线进行优化。该过程按照j=1,2,…,n的顺序执行,直到n个梯级水库链均已优化完毕为止。

从CBSA寻优过程可见,CBSA每次以梯级水库链为整体进行优化,可以有效地处理梯级系统内部复杂的水力耦合关系。
2.2 IPOA
与DPSA类似,POA也采用变量解耦策略进行降维。考虑N座水库构成的梯级水库链T个时段的优化问题,POA首先将问题的N·(T-1)个状态变量按时段分成T-1个固定的组,每组由同一时刻的N个状态变量组成;然后轮流对各组变量的值进行优化,直到N·(T-1)个状态变量的值稳定为止。因各组成员在整个优化过程中保持恒定,故称POA变量解耦策略为静态变量解耦策略。POA时间复杂度和空间复杂度分别为O(T·KN)和O(N·T)。更多POA详情参见文献[9]。POA良好的收敛性和鲁棒性使之成为当下最流行的水库群优化技术之一,然而,“盲目搜索”问题和“维数”问题严重限制了该算法在大规模水库群优化中的应用。
为了弥补上述缺陷,本文采用DVDS和扰动机制对POA进行改进。为了清楚起见,接下来采用决策变量(水库下泄)对相关问题进行描述。
2.2.1DVDS
DVDS基本思想为:①从问题的N·T个决策变量中抽取2N个(每座水库2个)对目标函数影响最显著的决策变量构建N维子空间;②在N维子空间中搜索,改善解的质量;③重复①—②,直至收敛。
2.2.1.1偶极子对
DVDS降维的关键是合理选取2N个决策变量。为了便于阐述,定义“偶极子对”的概念。在水库群联合调度中,通常各水库调度期初、末期的蓄水量给定,因此,对于某一天然来水过程,各水库调度期内的总下泄水量是确定的。根据水量平衡原理,水库某时段下泄量增加必然引起其他时段下泄量减少,且总增加量等于总减少量。根据上述原理,对水库i(i=1,…,N)的下泄轨线施加扰动,譬如令ji时段下泄增加ΔRi,ki时段下泄减少ΔRi。因作用于ji、ki时段的扰动大小相等方向相反,将此扰动定义为水库i的一个偶极子对,表示为(ji,ki)ΔRi,或者更简洁地表示为(ji,ki)。对于梯级水库链中的其他水库,可实施与水库i类似的操作。由于扰动叠加在水库下泄轨线上,一般而言,系统目标函数将发生变化。
2.2.1.2偶极子优化问题
对于水库i而言,其偶极子对中的ji、ki可在整数集{1,2,…,T}中任意取值,因此,总共存在T·(T-1)+1种偶极子对(其中,所有ji=ki的情况对应同1种偶极子对)。对于由N座水库构成的梯级水库链而言,考虑N座水库不同偶极子对的组合,总共有[T·(T-1)+1]N种偶极子对组合。在这些组合中,必然存在1种组合,作用于水库群下泄轨线上将产生最大的效益,称之为最优偶极子对组合。从所有偶极子对组合中寻找最优偶极子对组合的问题称为偶极子优化问题。DVDS正是通过求解偶极子优化问题,选取最优偶极子对组合对应的2N个决策变量构建N维子空间。以第m+1次迭代为例,偶极子优化问题可以表示为式(1):
(1)

2.2.1.3偶极子优化问题的DP模型
采用DP求解式(1)所示偶极子优化问题,定义阶段变量、状态变量和递推方程如下。
a)阶段变量。水库调度一般按时间顺序做出决策,因此通常将调度期划分为若干个时段,用1个时段表示1个阶段。考虑到偶极子优化问题的解是由不同水库的偶极子对构成,与时间相关性不大,并且,在梯级水库链中,水库i的最优下泄轨线必须在水库i-1的下泄轨线确定之后才能计算。因此,偶极子优化是按空间顺序做出决策。鉴于此,偶极子优化问题的阶段变量取水库索引i。对于由N座水库构成的梯级水库链,偶极子优化问题的阶段数为N。
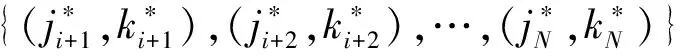
c)递推方程。对偶极子优化问题进行顺序递推计算,递推方程表示为式(2):
(2)

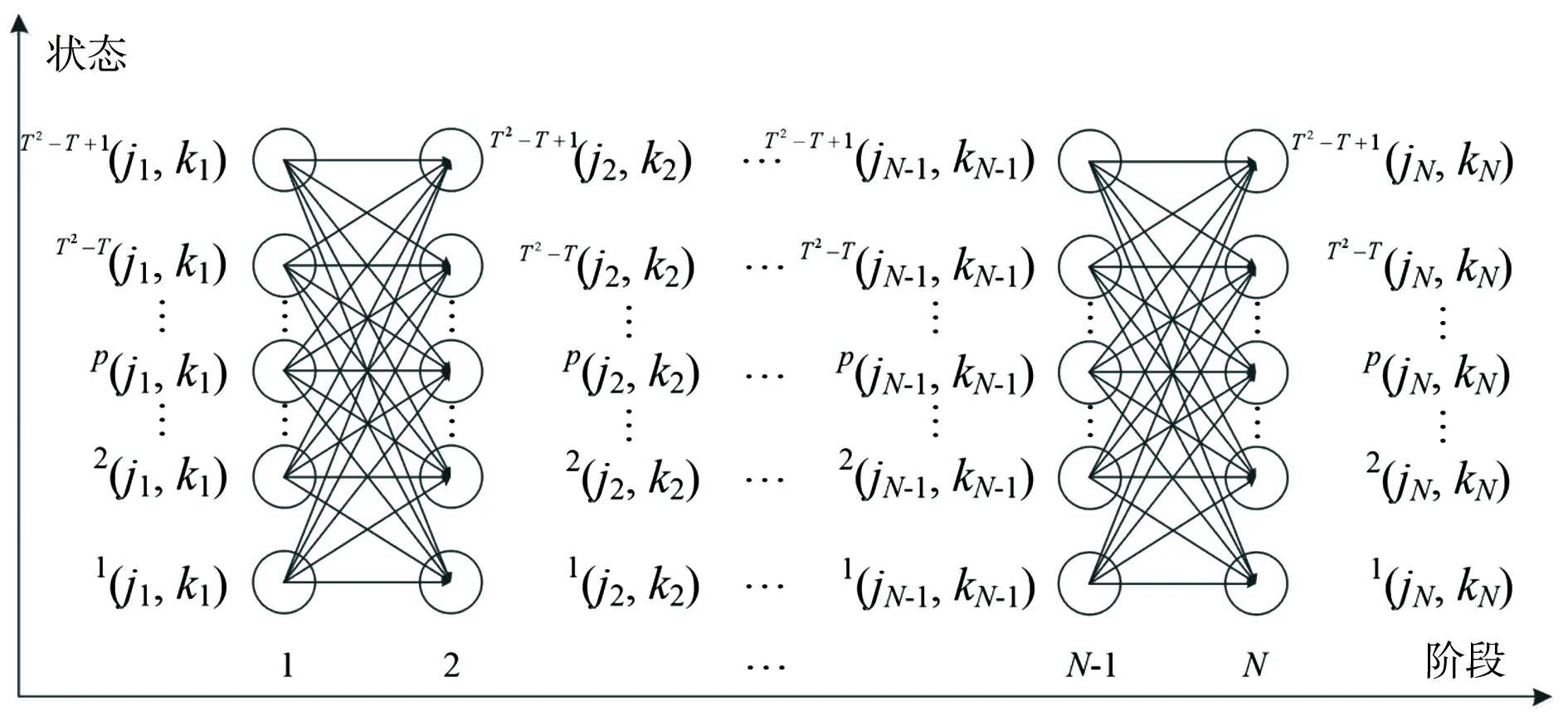
图2 DP求解偶极子优化问题原理
从图2可见,采用式(2),DP将N阶段问题分解为N个单阶段问题,避免了重复计算,提高了求解效率。因为每个阶段有T·(T-1)+1种状态,每个阶段须进行[T·(T-1)+1]2次目标函数计算,因此,DP的时间复杂度和空间复杂度分别为O(N·T4)和O(N·T2)。
2.2.2扰动机制
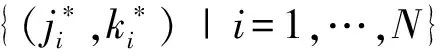
(3)
式中k——施加扰动的次数,在搜索开始时设置为0;kRi,t——施加第k次扰动后,水库i时段t的下泄量。
一般而言,在搜索的前期阶段,梯级系统效益会显著增长;随着搜索的发展(即k值增加),梯级系统效益的增长速度会逐渐降低;当k增加至某一临界值L时,梯级系统效益将停止增长;当k值超过L时,梯级系统效益开始下降。因此,k的最大取值应当为L。通常,L值可以采用试算法确定。L值确定后,通过使用递推式(3)(从k=0递推至k=L),梯级系统的下泄轨线可以得到改善。
由于IPOA的主要计算和存储需求来自偶极子优化问题求解,因此,IPOA的时间复杂度和空间复杂度与DP相同,分别为O(N·T4)和O(N·T2)。
2.3 算法组合
本文综合CBSA和IPOA 2种技术的优势对复杂水库系统进行降维:首先,采用CBSA将水库群优化问题分解为若干简单的“梯级水库链”优化子问题;然后采用IPOA轮流对各“梯级水库链”优化子问题进行求解,直至收敛。对于M座水库T个时段的优化问题,假设水库群系统分解为n个梯级水库链,则IPOA-CBSA求解流程见图3。IPOA-CBSA时间复杂度和空间复杂度分别为O(M·T4)和O(M·T2)。

图3 IPOA-CBSA算法流程
3 案例研究
3.1 “四水库”问题
以湖南沅水流域三板溪、白市、托口、五强溪4座季调节以上水库构成的梯级系统长期发电调度为例,研究IPOA-CBSA算法的性能。水库拓扑关系见图4,各水库特征参数见表1。
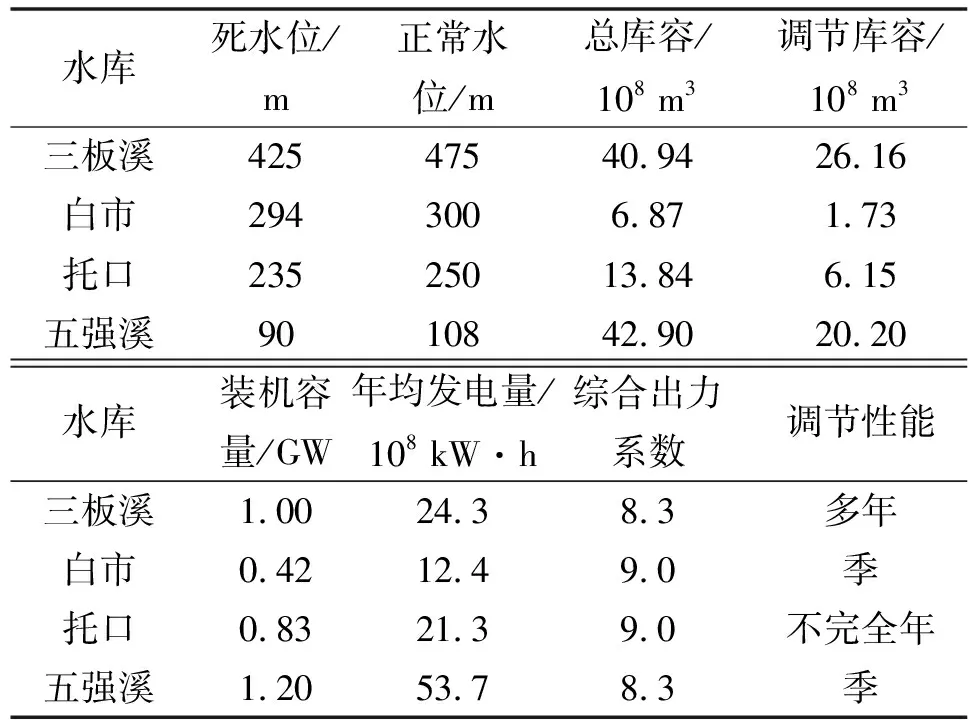
表1 水库特征参数

图4 “四水库”系统结构
该问题调度期为1 a,划分为12个时段(月),目标函数为水库群调度期内总发电量最大。为了方便公式化描述,按从上游到下游的顺序将4座水库依次编号为1、2、3、4,目标函数表示为式(4):
(4)
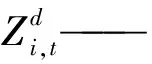
约束条件主要包括水库水量平衡方程、水库蓄水量上下限、水库下泄水量上下限、水库出力上下限、水库群总出力上下限、水库库容特性曲线、水库尾水位特性曲线和调度边界条件等。
采用流域2000年4月至2001年3月的月径流数据进行模拟计算。为了更好地展现IPOA-CBSA的性能,采用EPOA-DP[27]、DDDP、DPSA和POA进行对比分析。初始解按各时段水库出、入库平衡调节计算产生,初始解对应的目标函数值为17 222 945 MWh。采用EPOA-DP、DDDP、DPSA和POA进行求解时,各水库库容离散间隔为1.054×107m3,相应的流量步长为4 m3/s。ΔRi=1.054×107m3。在联想台式机上测试(3.40 GHz CPU,8 GB RAM),各算法最优指标对比见表2,各算法收敛过程对比见图5。
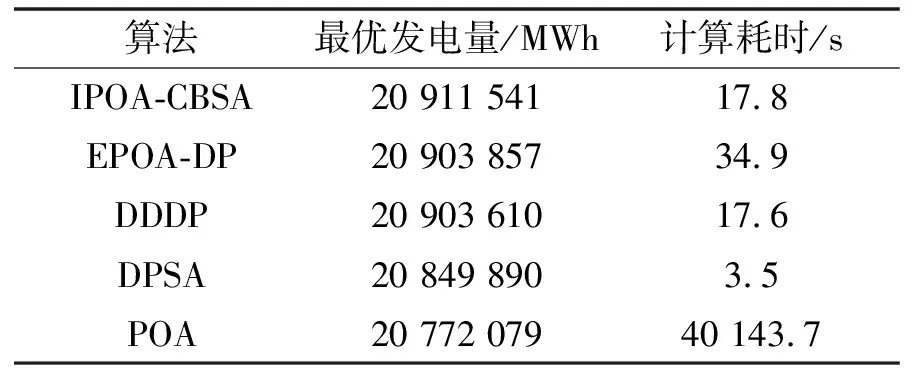
表2 不同算法求解“四水库”问题最优指标对比
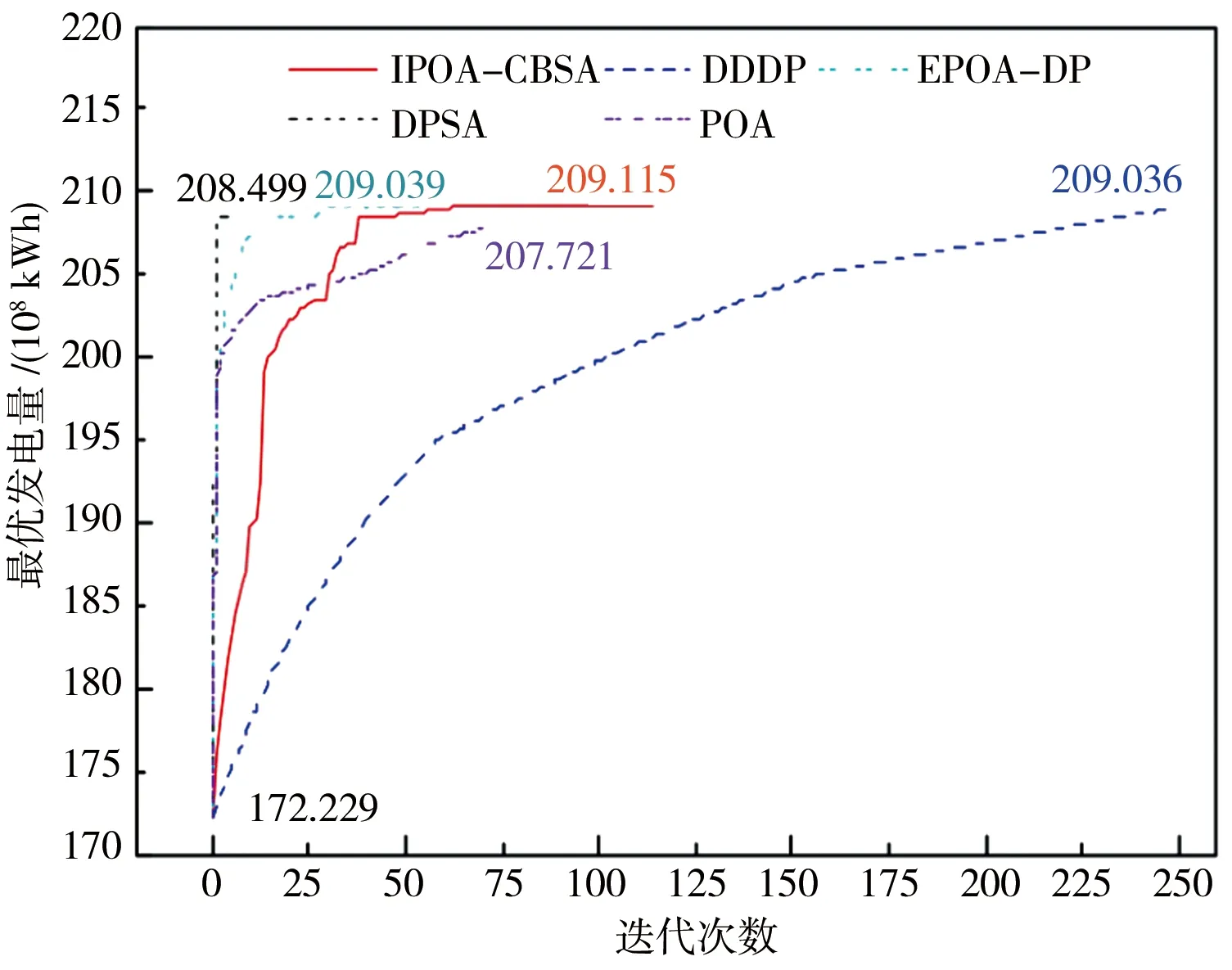
图5 各算法求解“四水库”问题收敛过程
由表2可知,5种算法的最优发电量,IPOA-CBSA最大,POA最小,IPOA-CBSA略大于EPOA-DP和DDDP,比DPSA增加0.62亿kWh(增幅为0.3%),比POA增加1.39亿kWh(增幅为0.7%)。
5种算法的计算耗时,DPSA最短,DDDP次之,POA最长。其中,POA计算耗时已超过11 h。POA耗时长主要是由两阶段问题求解的“维数障碍”引起。由于POA计算工作量与KN成正比,随着新的水库不断加入系统参与优化,可以预见,POA耗时将难以承受。
IPOA-CBSA计算耗时与DDDP基本相当。与DDDP相比,IPOA-CBSA最大的优势在于其计算工作量随M呈线性增长,而DDDP计算工作量随M呈指数增长(DDDP时间复杂度为O(T·32M))。可以预见,随着新的水库不断加入系统参与优化,DDDP计算耗时将远远大于IPOA-CBSA。
尽管EPOA-DP的最优发电量与IPOA-CBSA基本相当,但其计算耗时约为后者的2倍。与EPOA-DP相比,IPOA-CBSA最大的优势在于无需对水库状态进行离散(计算工作量与K无关),而EPOA-DP计算工作量正比于K2(EPOA-DP时间复杂度为O(M·T2·K2))。可见,随着精度要求不断提高,EPOA-DP计算耗时将远远大于IPOA-CBSA。
3.2 “十水库”问题
采用更复杂的“十水库”问题进一步验证IPOA-CBSA算法的性能。“十水库”问题是由Murray和Yakowitz引进文献,最先用于测试约束微分动态规划的性能[28]。Wardlaw和Sharif使用该问题测试GA的性能[29]。肖胜贤等[19]使用该问题测试改进POA-SA的性能。最近,Ahmadianfar等[30]使用该问题测试差分进化与粒子群混合算法的性能。与“四水库”问题相比,“十水库”问题不仅规模更大、系统结构更复杂,而且约束条件更多、更苛刻。“十水库”系统结构见图1。10座水库功能均以发电为主,调度期为1 a,划分为12个时段,目标函数为水库群调度期内发电效益最大,见式(5)。
(5)
式中bi,t——水库i时段t的效益系数。
“十水库”问题的约束条件主要有:水库水量平衡方程、水库蓄水量上下限约束、水库下泄水量上下限约束和调度边界条件等。水库1、2、3、5、6、8各时段均有天然来水注入,水库之间区间来水忽略不计。“十水库”问题相关参数的取值见文献[28]。
“十水库”问题的规模已经超过DP、DDDP、POA等算法的最大计算规模,该问题最优解对应的目标函数值为1194.44(可采用单纯形法求得)。为了更好地展现IPOA-CBSA算法的性能,采用EPOA-DP-SA[27]、改进POA-SA[19]、DPSA和GA[29]进行对比分析。IPOA-CBSA、EPOA-DP-SA和DPSA的初始解取自文献[28],初始解对应的目标函数值为1 080.983 6。IPOA-CBSA、EPOA-DP-SA、改进POA-SA、DPSA和GA分别经过22、151、5、3和2 500次迭代后返回各自最优值。在联想台式机上测试(3.40 GHz CPU、8 GB RAM),各算法最优指标对比见表3。
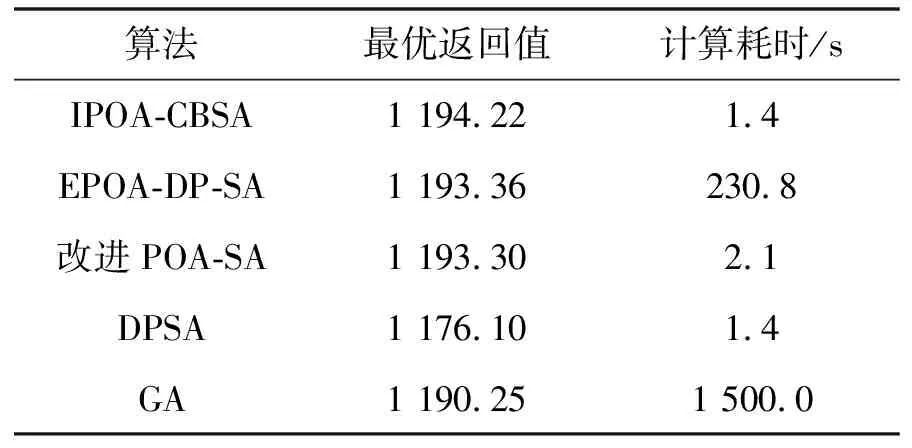
表3 不同算法求解“十水库”问题最优指标对比
由表3可见,5种算法中,IPOA-CBSA耗时最短,而最优返回值最大。IPOA-CBSA最优返回值略大于EPOA-DP-SA和改进POA-SA,较DPSA提高了1.5%,较GA提高了0.3%,达到“十水库”问题最优目标函数值的99.98%。IPOA-CBSA耗时仅为1.4 s,与改进POA-SA和DPSA较为接近,但远远小于EPOA-DP-SA和GA。进一步测试发现,当ΔRi=1×10-6时,IPOA-CBSA经过22次迭代后返回最优值1 194.44,最优返回值达到“十水库”问题最优目标函数值的100%,而耗时仅114.2 s。ΔRi=1×10-6时,IPOA-CBSA收敛过程见图6。
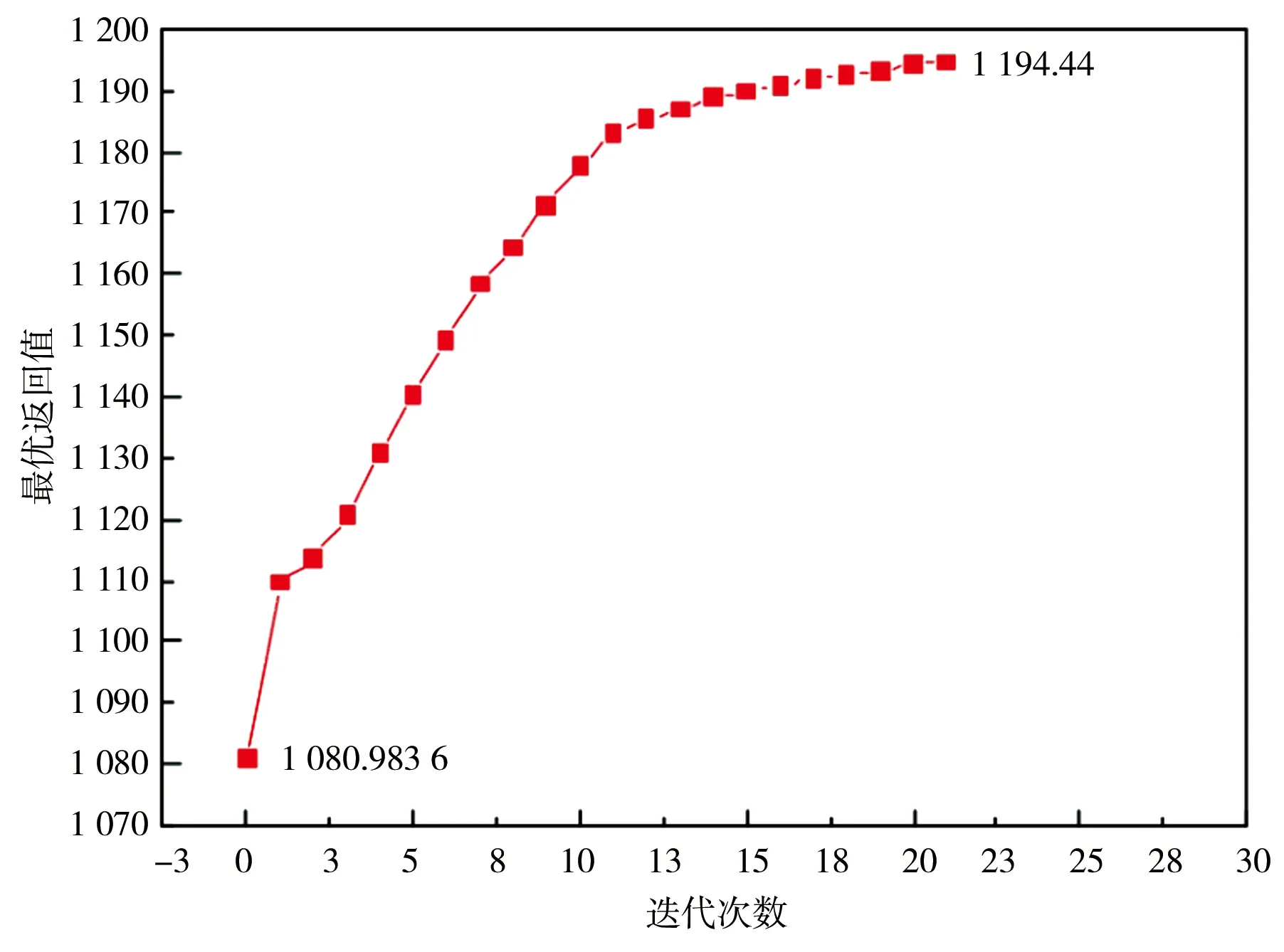
图6 IPOA-CBSA求解“十水库”问题收敛过程
4 结论
“盲目搜索”问题和“维数”问题限制了DPSA和POA在水库群联合优化中的性能。为了提高水库群优化问题的求解效率和解的质量,本文对DPSA和POA进行改进和综合,设计了一种组合降维算法。根据“四水库”问题和“十水库”问题的测试结果,本文得出以下结论。
a)采用CBSA将DPSA“单库轮流”优化模式拓展至“梯级水库链轮流”优化模式,“四水库”问题和“十水库”问题的优化效益分别提高了0.3%和1.5%,说明与DPSA相比,CBSA能够更好地处理梯级水库之间复杂的水力耦合关系,能够提高解的质量。
b)采用DVDS对POA静态变量解耦策略进行改进,“四水库”问题的发电量提高了0.7%,说明DVDS能够有效地弥补POA搜索的盲目性,能够提高解的质量。
c)通过在子问题求解中引进扰动机制和对2种改进算法进行组合,算法耗时明显缩短:对于“四水库”问题,POA计算耗时缩短了99.96%;对于“十水库”问题,IPOA-CBSA计算耗时不到2 s。说明IPOA-CBSA能够有效地缓解水库群调度的“维数灾”效应,能够提高求解效率。
d)IPOA-CBSA获得了“十水库”问题的最优解,在解的质量和求解效率上优于7种现有算法,说明IPOA-CBSA能够在保障解的质量的同时提高求解效率。与现有算法相比,IPOA-CBSA最大的优势在于,其计算工作量与水库数量为线性关系,具有应用于大规模复杂水库系统优化的潜力。
为了简化计算,建模时未考虑径流的随机性。考虑来水的不确定性,采用IPOA-CBSA对水库群进行长系列模拟计算,在此基础上挖掘水库系统优化调度规则,成为下一步研究重点。
