基于数据驱动的中小河流水位涨幅预报方法研究与应用

丁 武,林汉雄,王汉岗,张 炜,3*,杨 滨

(1.珠江水利委员会珠江水利科学研究院,广东 广州 510611;2.广州市黄埔区水务设施管理所,广东 广州 510611;3.水利部珠江河口治理与保护重点实验室,广东 广州 510611)

山洪灾害是造成中国人员伤亡的主要灾种,据统计,其所造成的人员伤亡数占全国因洪灾死亡失踪人口的40%[1]。2022年8月13日,四川成都彭州市龙门山镇后山突发暴雨引起龙槽沟区域突发山洪,造成7人死亡、8人轻伤;8月17日,青海大通县遭遇短历时强降雨诱发山洪灾害,造成26人遇难,5人失联。中小河流由于产汇流非线性特质显著,流域内布设的水文站网密度较为稀疏,大多缺乏长序列水文监测资料,且防洪基础设施薄弱,短历时强降雨极易诱发流域山洪灾害,并具有突发性强、历时短、破坏力大等特点,一直是中国防洪减灾工作的难点。

水位涨幅预测是山洪灾害防御的关键环节与技术难点,目前实现水位涨幅预测的方法可分为机理驱动分析方法、数据驱动分析方法以及数据驱动与机理驱动耦合方法。机理驱动分析方法主要基于流域降雨产汇流过程内在机理构建物理模型,推求降雨与成灾水位的关系,常见的机理模型以水文水动力模型为主。以分布式水文模型为代表的机理驱动模型在乏资料小流域地区的山洪预报中取得了较为广泛的应用[2-4],王坤[5]、孙仲谋[6]、孟天翔[7]使用水动力模型模拟山洪演进及沿程淹没过程,但受限于缺乏资料小流域的DEM、遥感信息(RS)等数据的不确定性以及模型参数的经验取值,使得分布式水文模型及水动力模型的预报精度不高。此外,张自航[8]采用陆气耦合模型构建了山洪预报模型,实现了气象和暴雨等致灾因素驱动下的山洪预报,然而气象预报模型本身误差较高,从而导致整体模型的预报精度不佳。随着水文监测技术、机器学习等人工智能技术以及高性能信息技术的迅猛发展,数据驱动分析方法越来越受青睐,数据驱动分析方法可屏蔽灾害演变过程所涉及到的错综复杂的物理机制,其主要是假设山洪与降雨等预报因子存在特定相关关系,并通过对历史监测数据的分析建立山洪与降雨等特征间的统计关系。基于数据驱动分析思路,赵龙等[9]利用随机森林算法有效识别山洪主要致灾因子,并以成灾水位反演建立了山洪灾害临界雨量预报模型。LIU等[10]利用支持向量机(SVM)构建了山区小流域洪水预报模型,以历史水位数据和气象预报数据等作为输入,对未来1～3 h的山洪进行预报,并考虑不同输入特征对预测结果的贡献度,预报成果较为准确。彭万兵等[11]通过考虑降雨强度、降雨量与前期土壤含水量耦合作用的影响,建立了降雨强度、有效累计降雨量、水位涨幅过程间变量统计关系的山洪预警模型。以机器学习或深度学习为手段构建山洪预报模型具有预报精度高、适应性强、计算简单且易于推广的特点,因此受到众多学者的认可[12-18]。数据驱动与机理驱动耦合方法则是以人认识自然规律的范式去从数据样本中挖掘规律,可有效整合数据驱动与机理驱动两者的优点,代表性的实现方法为先利用水动力模型模拟不同场景的雨洪过程,再利用聚类算法等机器学习算法学习水动力模型的模拟成果,以实现山洪灾害的快速预报[19]。

中小流域山洪灾害防御不仅受到灾害特性的影响,还受到防洪基础设施的制约,导致预警信息传播时间较长,因此中小河流山洪灾害预报的关键是延长灾害的预见期以及制定简易、推广性强的山洪预报模型,从而实现“早介入、早行动、早预防”,最大力度的保障人民生命财产安全。为此,从简易性、预报精度、可行性等多方面综合考量,本文提出3种中小河流水位涨幅预报模型,以典型流域广州市派潭镇对研究对象,分析模型的适用性及各自的优缺点,为中小流域的山洪灾害预报提供参考。

1 研究方法

1.1 水位涨幅预报因子筛选

水文预报中,预报模型的输入被称为预报因子。预报因子的筛选对于模型的构建至关重要,模型输入过多冗余信息不仅会加重模型的计算量,还会增大模型的预报误差;若模型输入缺失与输出具有重要成因关系的因子,则会导致预报精度直线下降。预报因子筛选主要通过度量输入因子与预报输出对象间的关联度大小,剔除关联度小和信息重复的因子,筛选信息量高、关联度强的预报因子。常用的预报因子选取的方法有互信息法、逐步回归法、主成分分析法、相关系数法、灰色关联分析法等。

本文以山洪水位最高涨幅作为模型的预测输出,原因在于增量序列能够放大影响径流的因子信号,更容易找到与其具有物理成因关系的气象因子[16],同时在一定程度上减少当前时刻水位对预报输出结果的扰动。

综合分析中小流域产汇流特性,选取流域内各雨量站点的雨强、累积雨量、降雨时序过程等降雨特征作为特征因子进行筛选,得到与水位涨幅具有强相关性的降雨特征作为模型的输入,共同构成模型的数据集。考虑到中小流域水位涨幅与降雨特征具有良好的线性关系,而相关系数法主要用于变量间线性相关性的度量,因此采用相关系数法分析中小河流水位涨幅与各预报因子间的相关性,其计算见式(1):

(1)

相关系数有正有负,即存在正相关和负相关,相关系数绝对值越大则表征特征间相关性越强。

1.2 中小河流水位涨幅预报模型构建

为实现山洪灾害的快速、精准预报,同时考虑到模型的简单实用性,本研究基于数据驱动分析法构建了3种河道水位涨幅预报模型,减少单一预报机制预报成果的扰动,强化不同应用场景下的山洪灾害预报。

1.2.1“降雨量-水位涨幅”关系预报模型

假设降雨量与水位涨幅具有广义线性关系,因此可通过建立降雨量与水位涨幅的回归模型,来实现山洪灾害预报模型构建。模型以与水位涨幅具有强相关关系的流域上游降雨量为输入,当特征因子筛选得到多个雨量站点的雨量可作为模型输入时,可将多个站点的雨量采用权值相加法确定,见式(2)。

(2)

为考虑预报模型的实用性,可考虑一元多项式或一元二次多项式逼近降雨量与水位涨幅关系。简单线性回归模型的表达为式(3):

Zw(P)=w1P+w2

(3)

二次回归的表达为式(4):

Zw(P)=w1P2+w2P+w3

(4)

式中w——需要优化的参数变量;Zw(P)——降雨量与水位涨幅回归模型。

可通过梯度下降算法、图解法等求解参数变量,确定最优的回归模型,回归的损失函数为式(5):

(5)

式中m——总洪水场次;Zk——第k场洪水的实测水位涨幅。

1.2.2基于相似分析的水位涨幅预报模型

基于相似分析的河道水位涨幅预报模型用于“寻找与预见期水文场景相似的历史水文场景,并以历史相似场景的水位涨幅情况为预见期水位涨幅提供参考”。相似性度量是相似分析模型的关键,即通过度量算法计算2个水文场景的综合相似程度。基于相似性分析法构建山洪灾害预报模型时,以山洪致灾因子作为水文相似性指标体系,即以特征因子筛选得到的水文特征作为相似性评估指标。计算各特征因子间的相似度,再基于相关性程度利用权重相加法或BORDA法等综合评定两水文场景的综合相似性。

常用的特征因子间相似性度量算法有余弦相似度量算法、欧氏距离法等。余弦相似度量算法计算见式(6):

(6)

欧氏距离法计算见式(7):

(7)

式中m——特征的时序总步长;Xi、Yi——两不同水文场景下特征第i个时间步长的特征值。

COSIN的值域为[-1,1],绝对值越接近1表示相似度越大;OUdist则是越小越相似。

1.2.3基于机器学习的水位涨幅预报模型

循环神经网络由其网络特性,在序列数据预测上具有独特的优势,常用的循环神经网络有RNN、LSTM、GRU。本研究采用GRU构建水位预报模型,其与RNN的不同之处在于,GRU是一种允许网络动态的控制时间尺度和各计算单元的遗忘行为的门控架构循环神经网络,能有效解决长序列数据预测问题中网络更新的梯度弥散与梯度爆炸问题。GRU与LSTM相比少了1个门控,主要由2个门控组成,其中更新门可以决定新的细胞状态是完全复制旧的状态,还是完全由新的信息所替换,或者处在2个极端之间,而复位门控制当前新信息中哪些部分可以用于计算下一个目标状态,2个门控都能独立的忽略部分状态信息,这使得GRU具备更少的参数量,也简化了计算,但在训练样本不大的情况下,GRU与LSTM能达到的预测效果基本一致,因此GRU更适用于中小河流预测小样本、高时效的应用场景。

GRU复位门的计算见式(8)、(9):

rt=σ(Wr[St-1,Xt])

(8)

(9)

更新门的计算见式(10)、(11):

zt=σ(Wz[St-1,Xt])

(10)

(11)

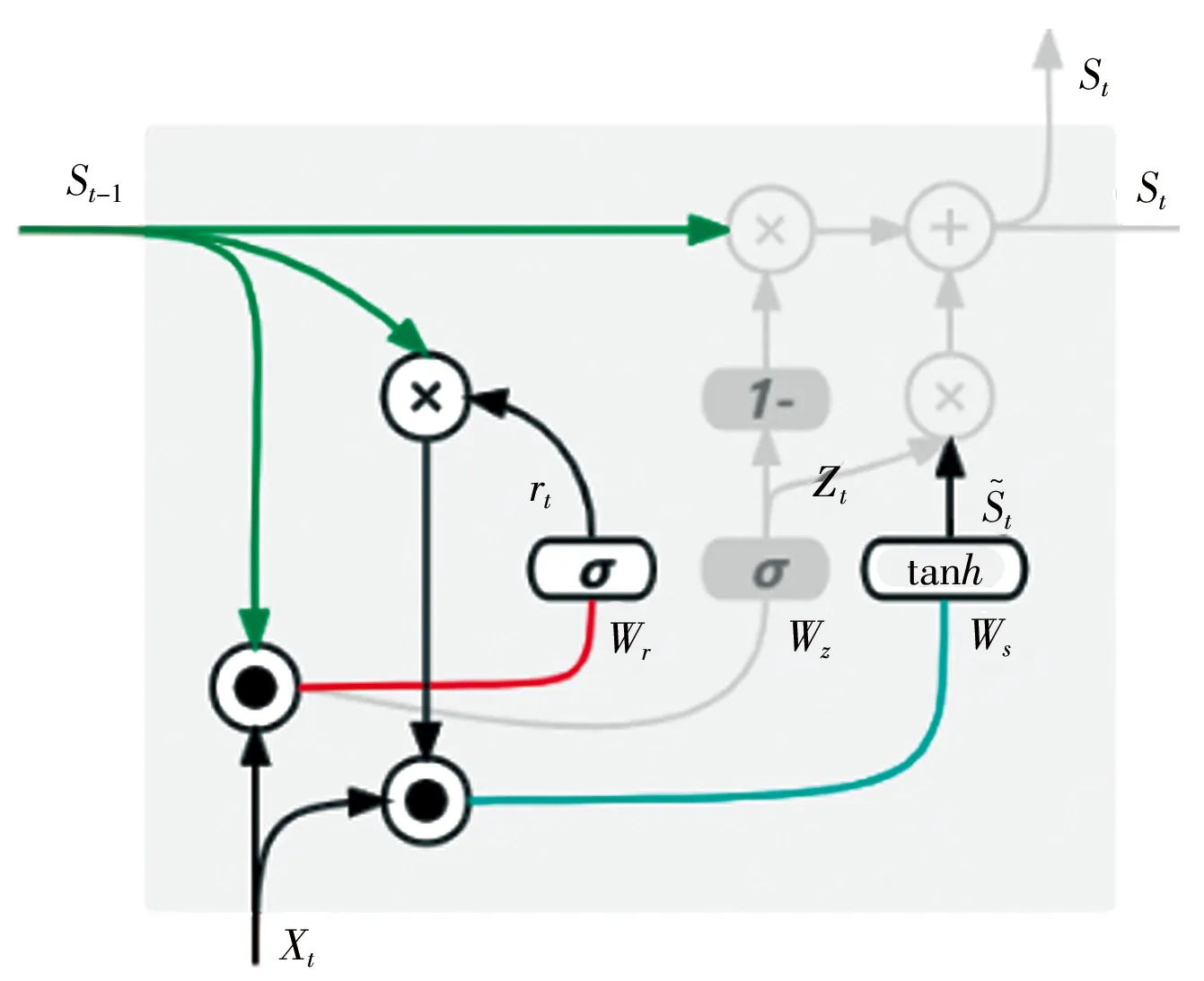
a)复位门

2 实例分析

本研究选取派潭河流域作为研究流域,派潭河位于广州市增城区境内,属增江一级支流,东江二级支流,自北向东南流向,流域面积302 km2,主河长度31.8 km,共有14条一级支流。派潭境内河网密集、山峦起伏,河谷盆地交错,地势北高南低,雨量充沛,多年平均降雨量为2 027 mm,且地处暴雨中心,降雨强度大。特殊的气候条件、地势地貌,决定了派潭镇暴雨具有发生频率高、降雨强度大、历时短、范围集中的特点,而来自山丘区的小流域因暴雨形成的山洪具有洪水过程尖峰、暴涨暴落的特点。加之上游小型水库调蓄能力有限、监测站点不足等问题,导致流域洪涝灾害频发。2020年6月4—9日,派潭镇累计降雨量达到548.81 mm,最大日降雨量达204.2 mm,全镇共有12个村22个合作社受到不同程度的水浸,共转移群众1 160人。2022年6月13日11时至14日11时,派潭录得最大1 h雨强92.5 mm,派潭河水位持续上涨。14日9点30分,派潭站最高水位达16.77 m,超警戒线3.27 m,全镇共有23个村社出现不同程度的水浸,紧急避险转移超1 500人,频发的山洪灾害严重影响派潭镇人民的生命财产安全和社会经济发展。

在增城区水文水资源在线监控管理平台数据库的基础上,利用数据收集方法,本研究共收集到派潭流域4个水位站、7个雨量站的逐小时历史水位、雨量实测数据。时间区间为2021年12月至2022年11月;水位站分别为三丫、高滩、七境、派潭;雨量站分别为派潭、三丫、七境、大岭山林场、上九陂村、飞碟训练中心、背阴村。所收集到的数据质量情况较好,水位数据存在极个别的空缺值及异常值,采用3σ法剔除异常之后,通过线性插值法予以填补。

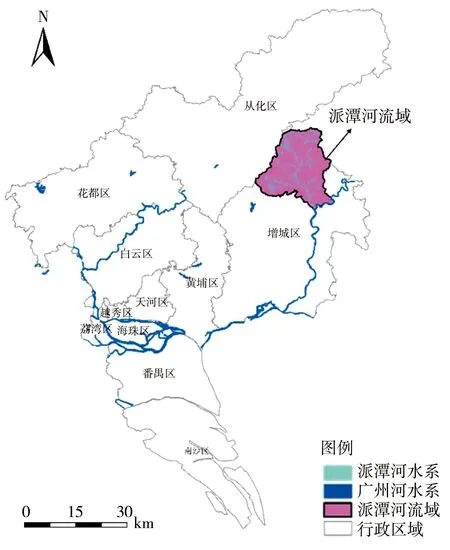
图2 派潭流域区位

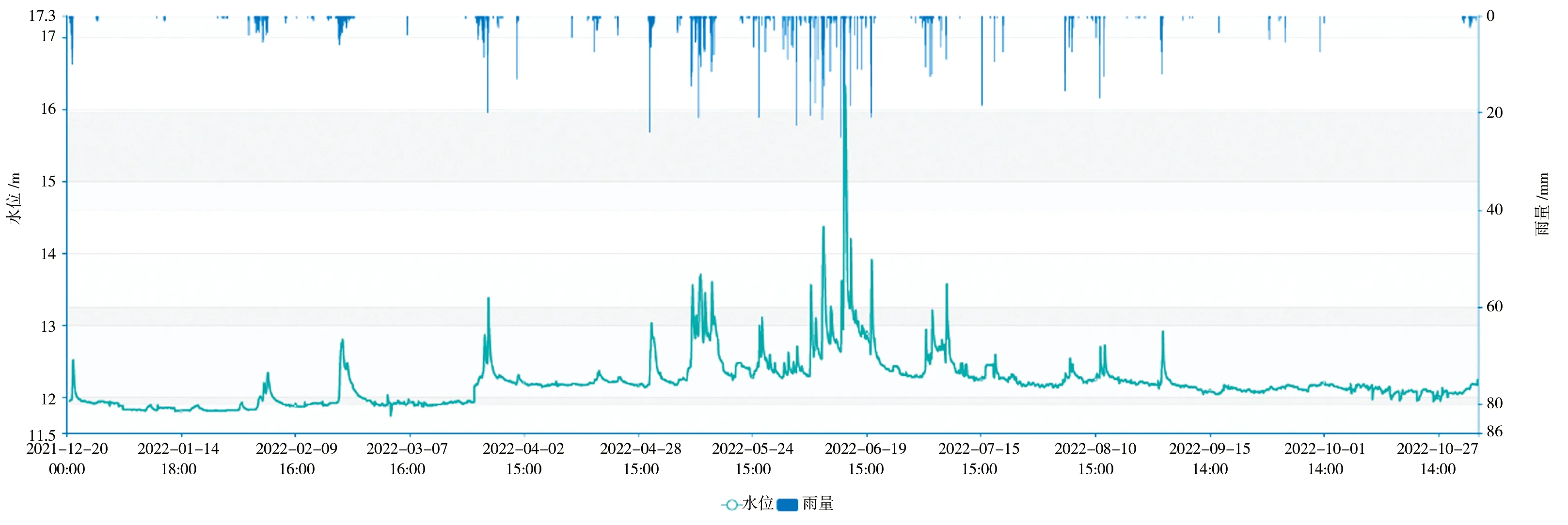
a)三丫站

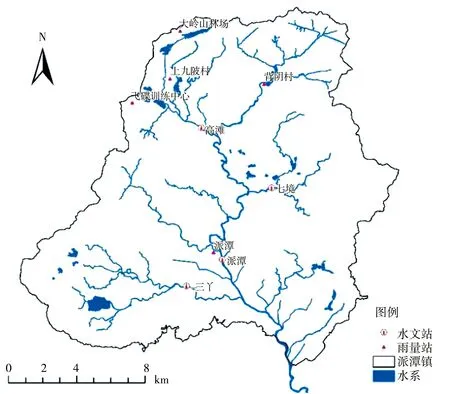
图4 雨水情监测站点分布

三丫与七境分别位于派潭河的支流高埔河与灵山河,通过物理成因分析可知其水位涨幅变化主要受到支流集雨面积上降雨量的影响。为此仅分析高滩、派潭站的水位与其上游降雨序列数据间的相关性,位于高滩站上游的雨量站有大岭山林场、上九陂村、飞碟训练中心;位于派潭站上游的雨量站有派潭气象站、七境、大岭山林场、上九陂村、飞碟训练中心、背阴村。相关系数计算见表1,可见,两站点水位变幅与其上游各雨量站点雨量都具有较强的相关性。

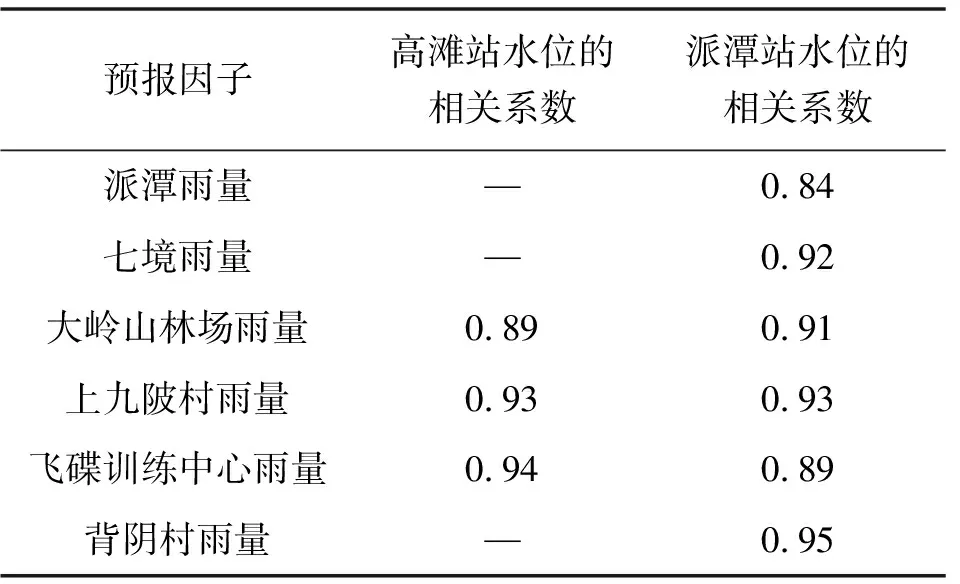
表1 相关系数计算结果

a)派潭流域基于“降雨量-水位涨幅”关系预报模型构建。对收集到的水位、雨量资料进行雨洪场次划分,从水位起涨点开始,满足水位涨幅阈值,至再次降到水位起涨点为一次洪水过程。以洪峰水位减去起涨水位作为场次洪水的水位涨幅;根据流域特性,选取以水位起涨时刻往前推8 h至洪峰水位出现时刻计算相关雨量站累计降雨量。高滩、派潭水位受多个相关雨量站影响,其累计雨量计算由相关雨量站场次洪水累计雨量依表2权重相加;所得到的若干场雨洪过程的累计雨量与水位涨幅量组成了模型构建数据集。为简化计算,在实例分析中采用了简单线性回归方法建立水位涨幅与累计雨量关系,回归成果见图5。以均方根误差(MSE)作为评估指标,选取使误差最小的参数作为“降雨量-水位涨幅”关系模型参数;以高滩、派潭两站为例,高潭站的MSE为0.15,派潭站的MSE为0.21,线性回归模型对历史“降雨-水位涨幅”数据拟合较好,可应用于实际的山洪预报预警工作中。

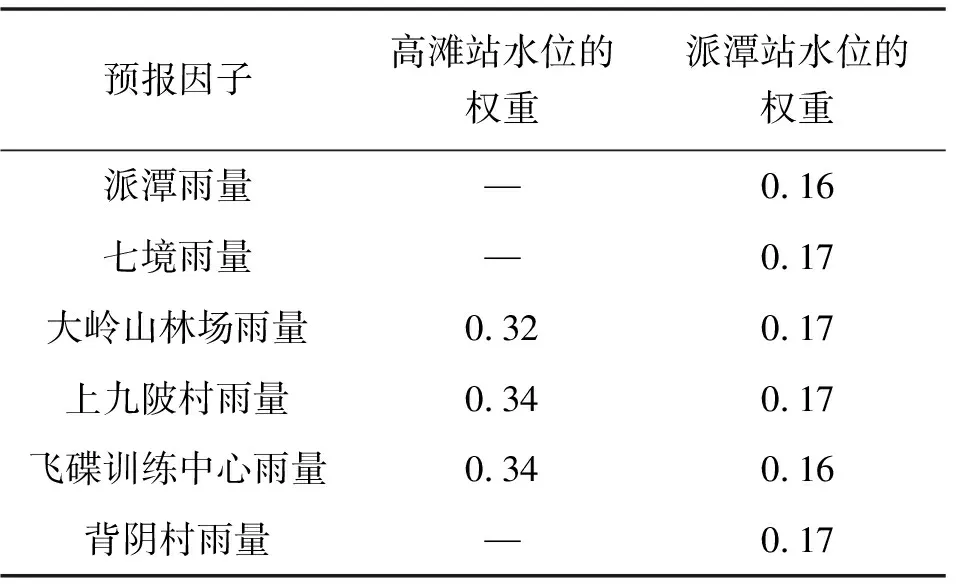
表2 相关系数经softmax处理后的权重取值

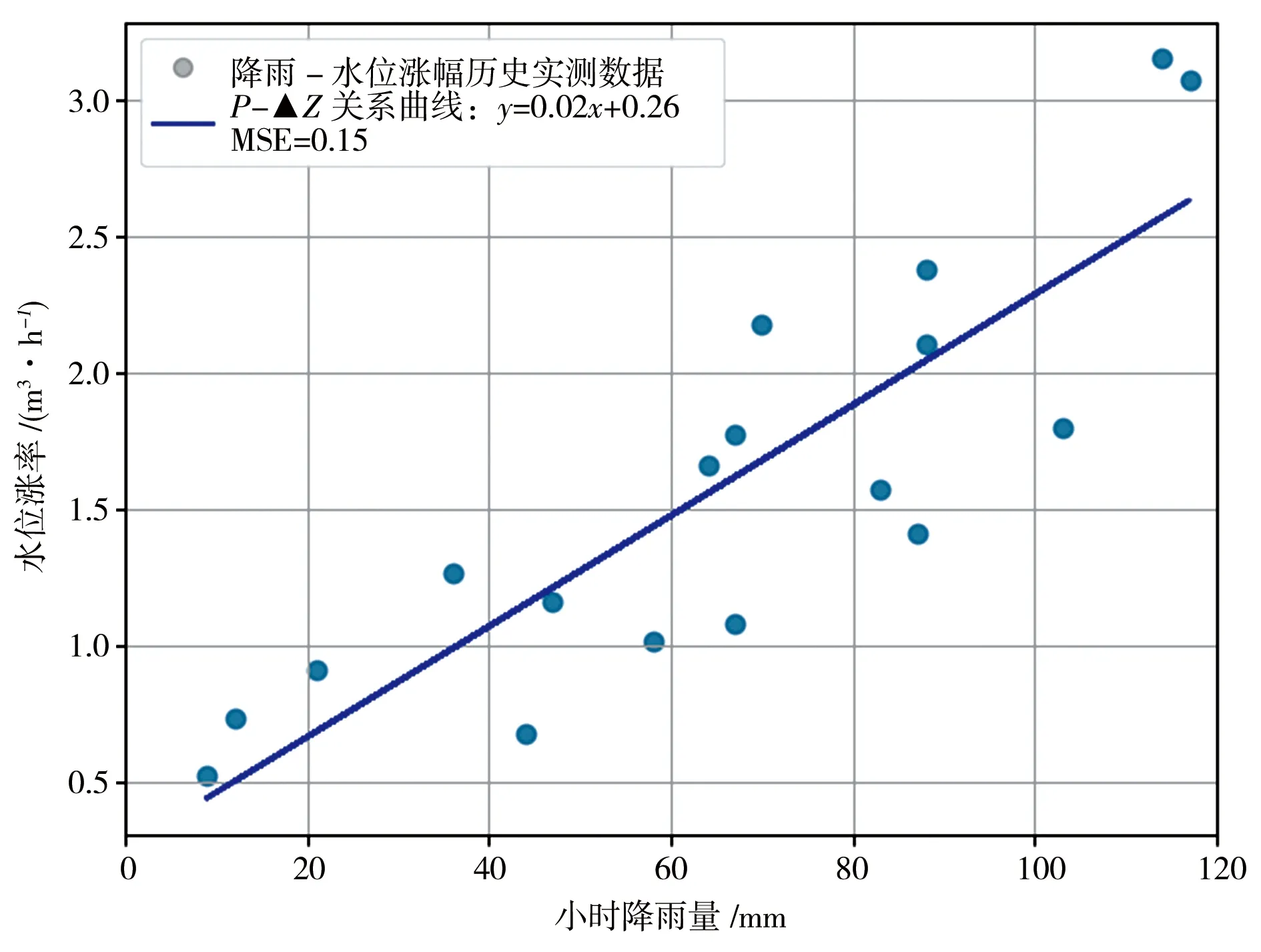
a)高滩站

b)基于相似分析的涨幅预报。采用窗口平移的方法计算出当前水文场景与各历史各水文场景间的相似性;以12 h作为场次降雨数据的序列长度,计算出各相关雨量站点降雨过程的欧氏距离,同样依据表2所示权重对各个雨量站点的欧氏距离进行相加,得到综合的欧氏距离,综合欧氏距离越小则两场景越相似,历史最相似场景的水位涨幅即为模型的预报输出值。选取2022年11月4日6点为水文场景为目标样本(实际中使用当前水文场景),从历史数据中寻找最相似历史水文场景,经过水位涨幅预报相似分析模型的计算,得到了与目标样本预见期水文场景最相似的历史场景,将其结果陈列(表3)。

表3 相似分析模型预报案例

c)基于机器学习的涨幅预报。通过GRU建立水位涨幅预报模型,模型的输入为降雨序列数据。网络结构拓扑图见图6,首先通过GRU单元提取降雨时间序列数据特征,派潭、高滩水位涨幅预报以多个站点的雨量数据为输入,可通过设置多个并行的GRU单元进行降雨特征的提取,其次通过全连接层实现对多个降雨序列信息的深度融合和特征提取,最终输出水位涨幅。

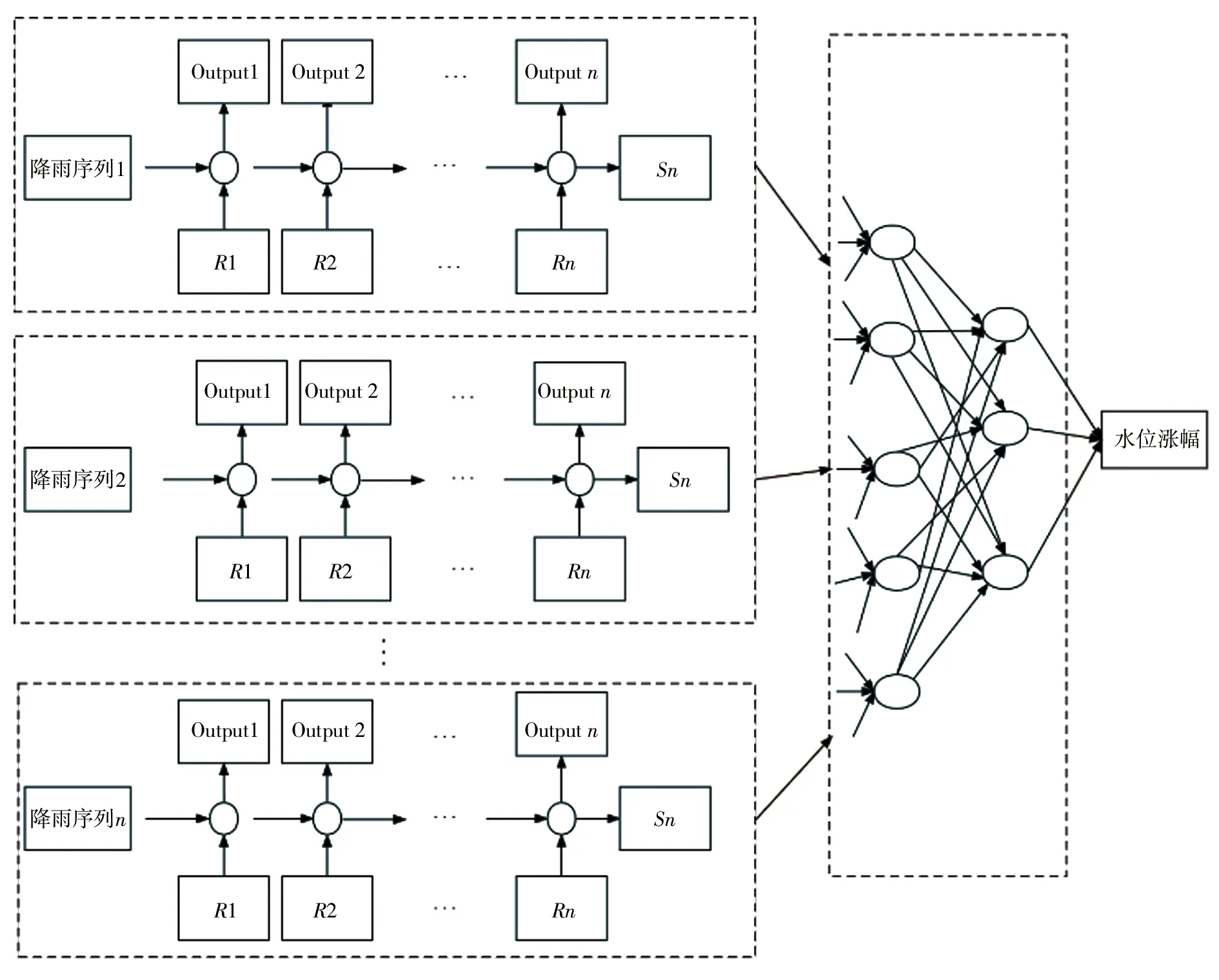
图6 网络拓扑

为综合评定3个模型的预报性能,并考虑模型在汛期与非汛期等不同时期预报精度的响应程度,将总数据集随机打散,按照7∶3的比例划分为训练样本集与测试样本集,据此分别建立了派潭流域4个水位站点的水位涨幅预报模型,以RMSE、预报误差百分比为评估指标评估模型的整体预报精度;其中预报误差百分比指预报值与实测值绝对误差小于某一阈值的样本数占总样本数的百分比,本研究采用了0.10、0.20、0.30 m 三种阈值。表4为派潭水位站的预报精度评估。

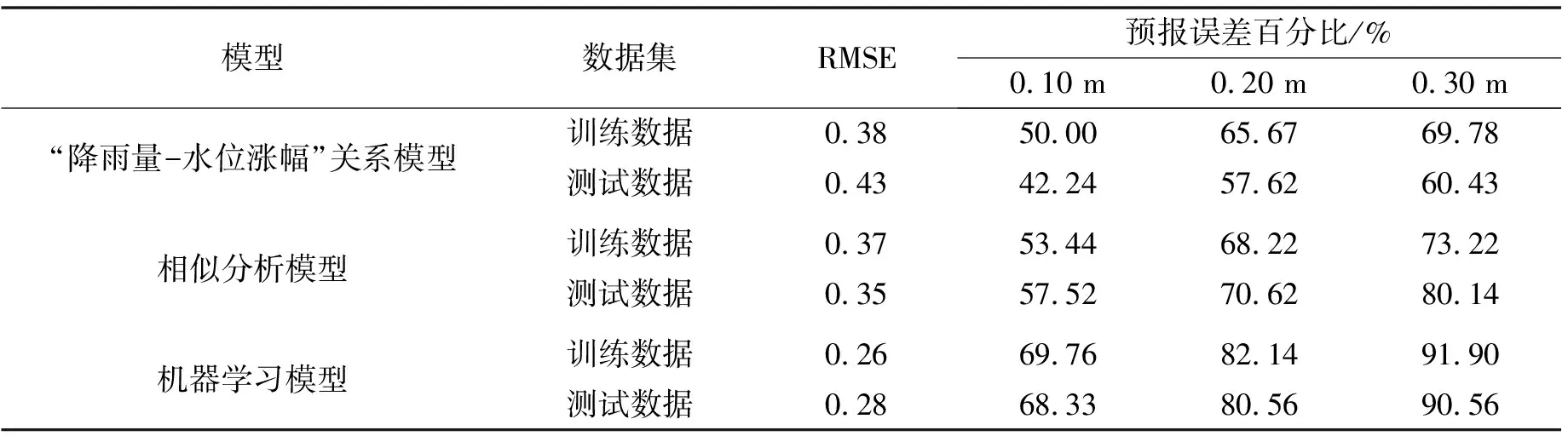
表4 派潭水位站预报精度评估

从预报精度评估结果分析,基于机器学习的水位涨幅预报模型的预报精度优于相似分析模型优于“降雨量-水位涨幅”关系模型。机器学习与相似分析模型预报误差控制在0.1 m以内的整体精度分别为68.33%、57.52%,控制在0.3 m以内的精度分别为90.56%、80.14%;“降雨量-水位涨幅”关系模型预报精度稍低,预报误差在0.1 m以内控制在42%左右,0.3 m以内控制在60%左右。

机器学习模型、相似分析模型对于样本集大小的敏感程度远高于“降雨量-水位涨幅”关系模型,模型精度随样本覆盖程度的提升提升。本实例研究选取了流域内近一年的雨洪资料,样本基本覆盖了汛期与非汛期等不同时期,因此机器学习模型与相似分析模型的预报精度较为理想,而基于线性回归的“降雨量-水位涨幅”关系模型模型复杂度低,样本数量饱和后,无法继续提升模型的预报精度。因此当流域实测资料较为丰富时,可使用机器学习模型、相似分析模型提升预报精度;当流域实测资料匮乏时,“降雨量-水位涨幅”关系模型也可提供山洪灾害预报提供支撑。

3 结论

本研究以派潭流域为案例分别建立了3种河道水位涨幅预报模型,经评估指标分析,机器学习与相似分析模型具有较高的预报精度;相似分析模型从历史资料中寻找相似场景,预报结果具有较好的认知性与可解释性,而机器学习模型则是黑箱模型;“降雨量-水位涨幅”关系模型则是建立起简单的累计降雨量与水位涨幅的回归关系,整体预报精度中等。相似分析模型与机器学习模型需要依托计算机设备进行辅助计算,而“降雨量-水位涨幅”关系模型可将模型结果绘制成图,对于基层人员的使用具有更强的可操作性。从预报便利性及预报精度上综合考虑,当中小流域具备计算机、APP等辅助设备支撑时,可采用机器学习与相似分析等多种模型进行山洪预报,提升预报精度;当缺乏计算机等基础设备的支撑时,“降雨量-水位涨幅”关系模型可为中小流域山洪预报预警提供便捷的计算方式。