基于PSOGA-WNN的废水处理系统软测量研究

刘煜辉,麦文杰,李小勇,赵银中,何新忠,黄明智*

(1.佛山市南海区狮山镇金迪水利投资建设有限公司,广东 佛山 528225;2.华南师范大学环境学院 广东省化学品污染与环境安全重点实验室 教育部环境理论化学重点实验室,广东 广州 510006;3.福建省环境保护设计院有限公司,福建 福州 350000)

废水参数的获取是废水处理的第一步。一般的废水参数主要有生化需氧量(BOD)、化学需氧量(COD)、pH、氨氮、磷、悬浮物、溶解氧、污泥涉及沉降比、浓度等。根据现有的废水处理技术,主要是人工间接测量再进行计算去对水质参数进行检测。这种方法耗时长,信息反馈具有一定的时滞性,会导致一些严重的后果。随着计算机技术的发展,基于神经网络的软测量技术开始兴起。该技术克服了人工测量的非实时性和耗时性,可对废水进行实时监测,实现对废水处理的智能控制。冯丽辉等[1]采用软测量建模技术构造多元线性回归模型,通过结合计算机模拟技术该模型能够实现多个废水出水水质参数的软测量预测,仿真实验结果表明,该模型的预测精度较高,有良好的拟合优度和一定的泛化能力。赵文文等[2]通过构建多核LSSVM模型并采用全局搜索能力较为出色的粒子群(PSO)算法对模型的超参数进行优化,最后应用于污水软测量建模中,仿真分析证实该方法进一步改善了回归模型的精确度和COD浓度的在线预估能力。纪广月[3]为解决传统BP神经网络所存在的收敛速度较慢和易于陷入局部最优的弊端,创建了一种通过云模型粒子群算法对BP神经网络的最佳初始权值和阈值进行优化的水质预测模型,并将训练后的模型应用到对西江水质的预测中,仿真结果证实,CPSO-BP水质预测的误差最小,且运算速度进一步提高,实现较快收敛。张秀菊等[4]针对传统水质预测方法存在预测精度不理想以及对实测数据要求较高的问题,创建基于BP神经网络的水质预测模型,仿真实验结果显示,所创建的BP神经网络模型预测效果较好,预测结果能很好地逼近真实值,可以用于潇河流域的水质预测。在上述所涉及的模型中,神经网络模型已较为成熟,但传统的BP神经网络易出现局部收敛问题,针对该问题,相关研究领域的学者研发出了基于小波变换理论的小波神经网络(Wavelet Neural Network,WNN),并将其应用于水文水资源领域[5-8]。通过小波基函数将输入信号分解成不同的频率通道,小波变换理论可以实现输入信号的平滑化处理,从而得到比原始信号更单一的分解信号,在对具有非线性和波动性特质的水质数据进行处理时,它也更具适应性[9]。

为确保污水厂一直处于稳定、安全的运行状态,首先需要对污水处理过程中的关键指标进行实时监测,例如化学需氧量(COD)、总固体悬浮物(TSS)、总磷(TP)、总氮(TN)、氨氮(SNH)等,通过监测这些指标可以反映出污水处理性能、出水质量和经济效益,进而根据监控结果来优化及控制污水处理过程。COD和SS作为污水处理厂的关键指标,若被过量排入受纳水体,将会导致严重的水污染事故,其造成的损失更是不可估计。因此,对污水处理厂出水COD和SS进行在线监测成为预防水污染事故成为预防水污染事故的关键。本文提出了一种基于小波变换的神经网络模型——WNN神经网络,并运用粒子群与遗传算法结合的PSOGA优化算法迭代寻优获取WNN神经网络的最佳初始值和阈值,对废水中的COD和SS进行预测,将小波理论和神经网络理论结合起来,实现对废水参数的预测,为目标废水的处理提供数据参考。

1 WNN神经网络

1.1 WNN神经网络结构

WNN神经网络同时结合了小波变换和神经网络的优点[10]。它是一种结合了小波变换的定位特性和神经网络的自学习能力的神经网络。WNN神经网络的网络结构是根据小波分析的理论确定的,它避免了 BP 神经网络[11]等在网络结构设计中的盲目性,并提高了容错性和逼近性能[12]。总体而言,对于处理同样的机器学习任务,WNN神经网络具有更加简单的网络层结构,收敛速度更快,准确率更高。

WNN神经网络与BP神经网络的主要不同是用非线性的Morlet 小波函数代替BP神经网络中常用的Sigmoid激活函数进行小波变化,然后传入输出层,WNN神经网络结构见图1[13]。

Morlet 小波函数:

(1)

式中f(x)——加权和;b——平移因子;a——尺度因子。

1.2 WNN神经网络原理

a)载入数据。为加快模型运行时的收敛速度,消除量纲的影响,需对训练和测试数据集中的6个输入水质参数数据:CODinf、Q、pH、SSinf、T、DO进行归一化处理,归一化是指使用特定的算法将数据保持在特定的范围内,6组输入数据使用相同的归一化操作。本研究中使用的方法是线性函数的归一化,见式(2):

(2)

式中xmax、xmin——单组输入数据的最大值、最小值;x、Y——数据归一化前后的值[14]。

b)网络构建。神经网络的网络构建过程主要是指通过解析数据特征,判断模型的输入层节点数(n)、隐含层网络节点数(m)以及输出层网络节点数(p),配置网络参数最大迭代次数maxgen和学习速率Lr。

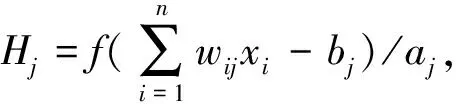
d)迭代优化。计算实际值与输出值的误差,根据误差精度和迭代次数不断调整参数。

e)计算误差。网络预测是水质参数预测的最后一步,其主要内容是利用训练好的小波神经网络对水质数据测试集进行预测,然后对预测数据进行反归一化并输出结果[16]。

2 PSOGA-WNN神经网络

2.1 PSOGA算法

粒子群算法(PSO)与遗传算法(GA)均为模仿自然界中生物活动过程的高智能算法,因此各有优缺点。在PSO算法中,由于粒子具有记忆能力,因而可以存储迭代寻优时的最优信息,它的局部寻优能力强,且收敛速度快;而GA则是具备较强的全局搜索能力;其交叉操作蕴含了信息互换的基本思路,而变异操作则可以增加种群的多样性,从而避免在迭代寻优过程中产生的早熟现象[17]。通过综合2种算法的优点,将GA的交叉和变异方法引入到PSO算法中,进而获得了整体性能更好的PSOGA算法。

2.2 PSOGA-WNN神经网络原理

PSOGA算法结合了遗传算法与粒子群算法的优点,具有快速的全局群体寻优的能力,能够较快的优化神经网络结构。利用PSOGA算法训练WNN神经网络的各参数,能够发挥神经网络的广泛映射能力,同时使网络快速收敛,使神经网络的权值、阈值及隐含层节点数达到最优,PSOGA算法训练WNN神经网络的流程见图2。

图2 PSOGA-WNN神经网络算法流程

其中算法关键步骤如下。

步骤一初始化模型参数。给定初始条件:即粒子个数n,最大惯性因子wmax、最小惯性因子wmin、学习因子η1、η2、种群规模popsize、交叉概率Pc、变异概率Pm、粒子更新速度Vmax、Vmin、迭代次数maxgen,神经网络各层的连接权值和隐含层数及节点数。

步骤二适应度函数设定。使用实际输出与期望输出的误差和作为适应度函数,以此评价粒子的搜索性能。适应度函数fit可表示为式(3):

(3)

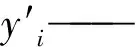
PSOGA训练问题的最优解就是迭代完成后适应度函数值最低的粒子,此时的训练误差也最小。

步骤三确定种群。神经网络参数优化问题的最优解就是通过计算得到粒子群中粒子的最佳位置,即粒子的位置向量z所包含的隐含层节点数以及连接权值和阈值。

神经网络输入层的节点数量为n,输出层节点数量为m,隐含层节点数量为p;输入层i到隐含层j的连接权值为wij,隐含层到输出层的连接权值为wjk,隐含层单元的阈值为bj,输出层单元的阈值为aj,则位置向量pop可表示为式(4):

pop=[p,w11,…,wnp,b1,…,bp,w11,…,wpt,a1,…,at]

(4)

步骤四初始化。在限定的区间内随机初始化隐含层节点粒子的位置和速度。

步骤五评价粒子。利用适应度函数计算粒子在每一次迭代过程中的适应度值。

步骤六更新个体最优值和全局最优值。评价粒子当前适应度值与其最好位置的适应度值,判断是否为最佳的位置,并比较所有的pbest和gbest,更新gbest。

步骤七惯性权重更新。惯性权值w,采用线性递减方法来更新:

(5)

式中wmax、wmin——w的最大值、最小值,通常wmax=0.9,wmin=0.4;t——当前迭代步数;tmax——最大迭代步数。

步骤八位置和速度的更新。由步骤六生成的pbest和gbest进行位置和速度的更新。

位置更新见式(6):

popid=popid(t)+0.2×vid(t)

(6)

速度更新见式(7):

vid(i+1)=w×vid(i)+η1rand()(pid-zid(t))+η2rand()(pgb-zid(t))

(7)

式中vid——粒子的速度;w——惯性权重;t——迭代次数;η1、η2——学习因子;popid——粒子的位置; rand()——介于[0,1]间的随机数;pid——粒子最好位置,即个体极值;pgb——种群最佳位置,即全局极值。

此外,为使粒子速度变化不致过大,可设置速度上限vmax,程序代码如下:

Ifvid(t+1)>vmax

vid(t+1)=vmax

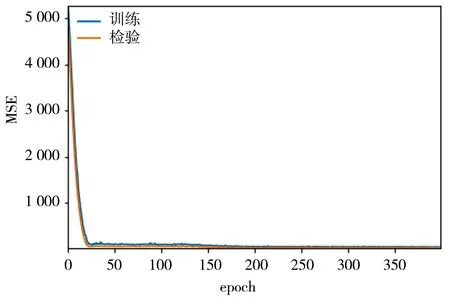
Else ifvid(t+1)

vid(t+1)=vmin

end

同理,为限制粒子的位置,可设置位置上限popmax,程序代码如下:

If popid(t+1)>popmax

popid(t+1)=popmax

Else if popid(t+1)

popid(t+1)=popmin

end

步骤九位置的交叉和变异。按照设置好的交叉概率Pc和变异概率Pm对更新的位置pop进行交叉和变异操作,然后进行适应度计算更新pbest以及gbest。

步骤十迭代停止。达到最大迭代次数,算法停止。

步骤十一生成最优解。算法停止时的全局最优值,即为神经网络各层网络的连接权值及阈值。

步骤十二权值训练。将步骤十一优化得到的结果,生成神经网络结构所需的所有参数,隐含层节点数、网络权值和阈值,作为WNN网络的权值和阈值。

整个WNN神经网络的结构及权值、阈值有了初步优化,但这并不是最终的网络结构,WNN网络本身也包含了训练、学习的步骤,利用PSOGA算法获得的网络结构再次进行自我训练和优化,进一步寻找神经网络的最优解,进行局部寻优,从而提高神经网络的搜索效率以及收敛程度,获得良好的模式识别网络。

3 仿真结果与分析

3.1 数据预处理

仿真实验中使用的是广东省东莞市某造纸厂废水处理系统曝气池的监测结果[18],包括CODinf、Q、pH、SSinf、T、DO、CODeff、SSeff8组实测数据,每组数据170个样本,采用CODinf、Q、pH、SSinf、T、DO 6个水质参数对CODeff和SSeff进行预测。由于WNN神经网络同时预测2个变量效果并不是很好,因此CODeff和SSeff应分别进行预测。预测统一采用前140组实测数据作为训练样本,测试和检验样本都选择为后30组数据。

3.2 预测性能评价指标

为了检验预测的精确度,使用均方根误差(RMSE)、平均绝对百分比误差(MAPE)和相关系数(R2)3个评价指标来检测,其计算见式(8)—(10)。n是测试样本预测数据的量,y′为模型训练之后得出的预测值,y为实测值。RMSE和MAPE反映出真实值和预测值之间偏差的侧度,RMSE和MAPE越小,表明预测值越接近真实值,即预测的效果越好,而R2表征拟合优度,越接近于1表示拟合数据能力越好。

检测值RMSE 的计算方法为:

(8)

检测值R2的计算方法为:

R2=

(9)

检测值MAPE的计算方法为:

(10)

3.3 试验结果

WNN神经网络是一种混合小波分析和神经网络模型,主要用于时间序列预测。分别使用小波神经网络进行运算,采用小波神经网络的结构为6-4-1,即输入层网络节点6个,隐含层网络节点为4个,输出层网络节点为1个。在样本学习率分别为Lr1=0.01和Lr2=0.000 1的前提下,经过1 500步运算后训练完成。测试集预测结果与检验样本结果对比见图3、4。

图3 测试样本出水COD真实值和预测值曲线

图4 测试样本出水SS真实值和预测值曲线

图5、6为PSOGA-WNN模型训练样本和检验样本的误差曲线。由图可知,训练误差曲线随着网络训练次数的增加而趋向于0。为防止发生过拟合,模型采用了“早停止”策略,即当模型的MSE在连续的20次迭代中都无明显变化,模型训练停止,由图可知,对于出水COD的预测,在epoch=400时,模型停止了运行;对于出水SS的预测,在epoch=600时,模型停止了运行。由模型的训练误差曲线可知,模型检验样本误差和训练样本误差相差不大并未发生过拟合,且模型在训练时能够较快地拟合数据使其趋于真实值,数据收敛后其误差能持续保持稳定。图3、4表明,构建神经网络,利用历史数据对废水参数中CODeff和SSeff进行预测。通过真实值和预测数值比较表明PSOGA-WNN神经网络具有强大的预测能力,进一步考虑PSOGA-WNN神经网络的功能。在本文中,使用RMSE、MAPE和R2的性能评估指标比较了PSOGA-BP神经网络、PSOGA-WNN神经网络、PSO-WNN[19]神经网络以及GA-WNN[20]神经网络的预测结果。结果见表1。

表1 预测性能评价指标结果

图5 出水COD预测误差曲线

图6 出水SS预测误差曲线

由表1可知,在CODeff的预测中,RMSE(PSOGA-WNN)R2(GA-WNN)>R2(PSO-WNN)>R2(PSOGA-BP);在SSeff的预测中,RMSE(PSOGA-WNN)R2(GA-WNN)>R2(PSO-WNN)>R2(PSOGA-BP)。所以,无论是预测CODeff还是预测SSeff,PSOGA-WNN神经网络明显优于其他神经网络。同时,由表中数据可知,测试样本和训练样本的RMSE、R2以及MAPE差别并不大,这说明模型的测试样本和训练样本预测误差相当,表明模型具有较好的泛化以及拟合能力。

4 结论

小波变换和神经网络的优点完美结合,WNN神经网络具有学习能力强、收敛速度快、精度高、稳定性强等优点,而结合PSOGA的PSOGA-WNN神经网络通过对权值和阈值进行优化进一步提升了神经网络的性能。通过PSOGA-WNN神经网络与PSOGA-BP以及PSO-WNN、GA-WNN的仿真实验结果对比可知,对于CODeff的预测,PSOGA-WNN神经网络的RMSE比PSOGA-BP降低了25.6%,比PSO-WNN降低了20.2%,比GA-WNN降低了19.0%,PSOGA-WNN神经网络的MAPE比PSOGA-BP降低了21.1%,比PSO-WNN降低了17.6%,比GA-WNN降低了19.5%,而R2则比PSOGA-BP提高了18.6%,比PSO-WNN提高了17.9%,比GA-WNN提高了15.5%;对于SSeff的预测,PSOGA-WNN神经网络的RMSE比PSOGA-BP降低了39.5%,比PSO-WNN降低了16.2%,比GA-WNN降低了8.1%,PSOGA-WNN神经网络的MAPE比PSOGA-BP降低了35.8%,比PSO-WNN降低了14.5%,比GA-WNN降低了6.6%,而R2则比PSOGA-BP提高了27.2%,比PSO-WNN提高了7.3%,比GA-WNN提高了3.7%。由该对比结果可得,WNN神经网络相比于BP神经网络,其预测精度更高,而将PSO和GA算法的结合在一起的PSOGA算法相比于单一的PSO和GA算法具有更好的寻优性能。这表明PSOGA-WNN是一个拟合效果极佳的水质预测模型,使用PSOGA-WNN神经网络的预测可以充分逼近特定水质数据的实际值。目前的研究可以在水质预测领域进一步研究水质数据中的多元关系,进一步提高PSOGA-WNN神经网络模型的预测精度和稳定性,同时,寻找更加有效的参数优化算法来优化模型,提高模型的预测性能。