一种双层圆孔阵列全介质超表面完美吸收器

许瑞星,吕晓龙,郭云胜

(内蒙古科技大学 理学院,内蒙古 包头 014000)

全介质超表面与金属超表面相比,具有耐高温、耐腐蚀、欧姆损耗低等优点[1-3],在无线通信[4]、宽带吸收[5]、滤波器[6]、频率选择[7]、传感[8-9]、天线[10]和生物医学[11-12]等领域有广泛的应用。2016 年,Michael 等提出全介质惠更斯超表面完美吸收器[13],开启了全介质超表面在吸波领域的重要应用。一般而言,把具有适当损耗的高介电常数圆柱体周期性地嵌入到低介电常数材料中,调整圆柱体高度与直径的比值,使入射电磁波在介质圆柱内激发的电偶极子和磁偶极子谐振于同一频率,反射率和透射率都会变为零,从而实现了全介质惠更斯超表面的完美吸收。为了验证上述理论,Liu 等采用绝缘衬底上的硼掺杂硅工艺制作了太赫兹波段实验样品,测试结果表明在1.011 THz 处吸收率为97.5%,与完美吸收的微小差距是由样品的粗糙度造成的[14]。2017 年,Ming 等基于简并临界耦合理论进一步阐述了惠更斯超表面完美吸收器的工作原理[15],为设计完美吸收超表面提供了充足的理论依据。

然而,对于完美吸收全介质超表面实验样品的制备而言,采用硅掺杂工艺在衬底材料上制作具有一定损耗的谐振器,存在难度大、周期长、成本高等问题,严重限制了全介质超表面的应用。考虑到微波段完美吸收超表面在电磁隐身和屏蔽等方面具有较大的应用前景[16-19],本文探究一种微波段全介质超表面完美吸收样品的简单结构和制作方法。研究结果表明,由损耗较大的磁性复合材料吸波片和损耗极小的聚四氟乙烯陶瓷复合材料组合成双层基板,在其上排列的周期性圆孔阵列能够实现惠更斯全介质型超表面的近似完美吸收。

1 模型与仿真

本文采用Comsol Multiphysics 软件对圆孔阵列全介质超表面进行仿真。一般而言,电磁波在某个频率处的完美吸收与超表面结构的几何和材料参数有极大关系。为寻找圆孔阵列超表面实现完美吸收的一般规律,首先在一定材料参数的介质板上设计圆孔阵列结构,通过优化圆孔结构的几何参数,使超表面在外界电磁波的激发下产生的电偶极子和磁偶极子在同一频率处谐振;然后优化材料损耗,找出完美吸收所需的最佳值,从而完成了超表面完美吸收样品的设计。图1(a)为构建的介质圆孔阵列超表面样品的单元结构,其中P和D分别是单元结构的周期和直径,t是圆孔的厚度。图1(b)是单元结构在xy平面上的 3×3 阵列。图1(a)的仿真模型中,波矢量沿z方向,电场沿x方向;与x和y方向垂直的平面分别设置为周期性边界条件,与z方向垂直的两个平面设置端口。在超表面样品设计中,通过反射系数S11和透射系数S21计算得出反射率R(ω)=和透射率T(ω)=,可得到吸收率A(ω)=1-R(ω)-T(ω) 随样品的几何和材料参数的变化情况。

图1 (a)全介质超表面的单元结构;(b)超表面单元在xy 平面的 3×3 阵列Fig.1 (a) Cell structure of all-dielectric metasurface;(b) 3× 3 array of metasurface units in the xy plane

图1(a)中单元结构的大小为16 mm,厚度为5 mm,介质材料的相对介电常数为11,介质损耗角正切为0.03,吸收率随圆孔直径D的变化规律如图2(a)所示。从图2(a)可清楚地看出,当圆孔直径从11.2 mm 变化到15.2 mm 时,从低频段开始出现的两个吸收峰逐渐合并为一个峰,然后又逐渐分离。以圆孔直径为11.2 mm 的两个吸收峰为例,分析它们的电磁谐振模态可知,9.8 GHz 处的吸收峰为电谐振峰,其模态的电场与电偶极子[20-22]相似,如图2(b)所示;11 GHz 处的吸收峰为磁谐振峰,其模态的磁场与磁偶极子[20-22]相似,如图2(c)所示。当圆孔直径为13.2 mm时,电谐振峰和磁谐振峰在11.3 GHz 处重叠。由于介质损耗不是最佳值,谐振峰重叠处的吸收峰仅为75.3%。

图2 (a)圆孔直径不同的情况下,超表面的吸收谱中电谐振峰(垂直实线)和磁谐振峰(垂直虚线)的变化;圆孔直径D=11.2 mm 时(b)9.8 GHz 处的电场模和(c) 11 GHz 处的磁场模Fig.2 (a) Variation of the electric (vertical solid line) resonance peaks and magnetic (vertical dashed line)resonance peaks in the absorption spectrum of the metasurface for different circular hole diameters;(b) Electric field mode at 9.8 GHz and (c) magnetic field mode at 11 GHz when the circular hole diameter D is 11.2 mm

固定圆孔直径为13.2 mm,优化介质损耗角正切值,吸收率随损耗角正切的变化结果如图3(a)所示,可以看出: 介质损耗角正切值从0.05 变化到0.15,在11.3 GHz 处的吸收率先增大后减小;当介质损耗角正切tanδ=0.1 时,接近于完美吸收(99.95%)。另外,为了验证圆孔阵列是实现超表面完美吸收的关键因素,对无圆孔阵列介质平板进行仿真对比。介质平板的厚度和材料参数与圆孔阵列超表面中的相应参数完全相同,材料的介质损耗角正切变化范围也相同。介质平板对电磁波的吸收率随介质损耗角正切变化的规律如图3(b)所示。从图3(b)中可清楚地看出,当介质损耗角正切值逐渐增大时,介质平板的吸收率都较低,因此圆孔结构对超表面实现完美吸收起到关键作用。

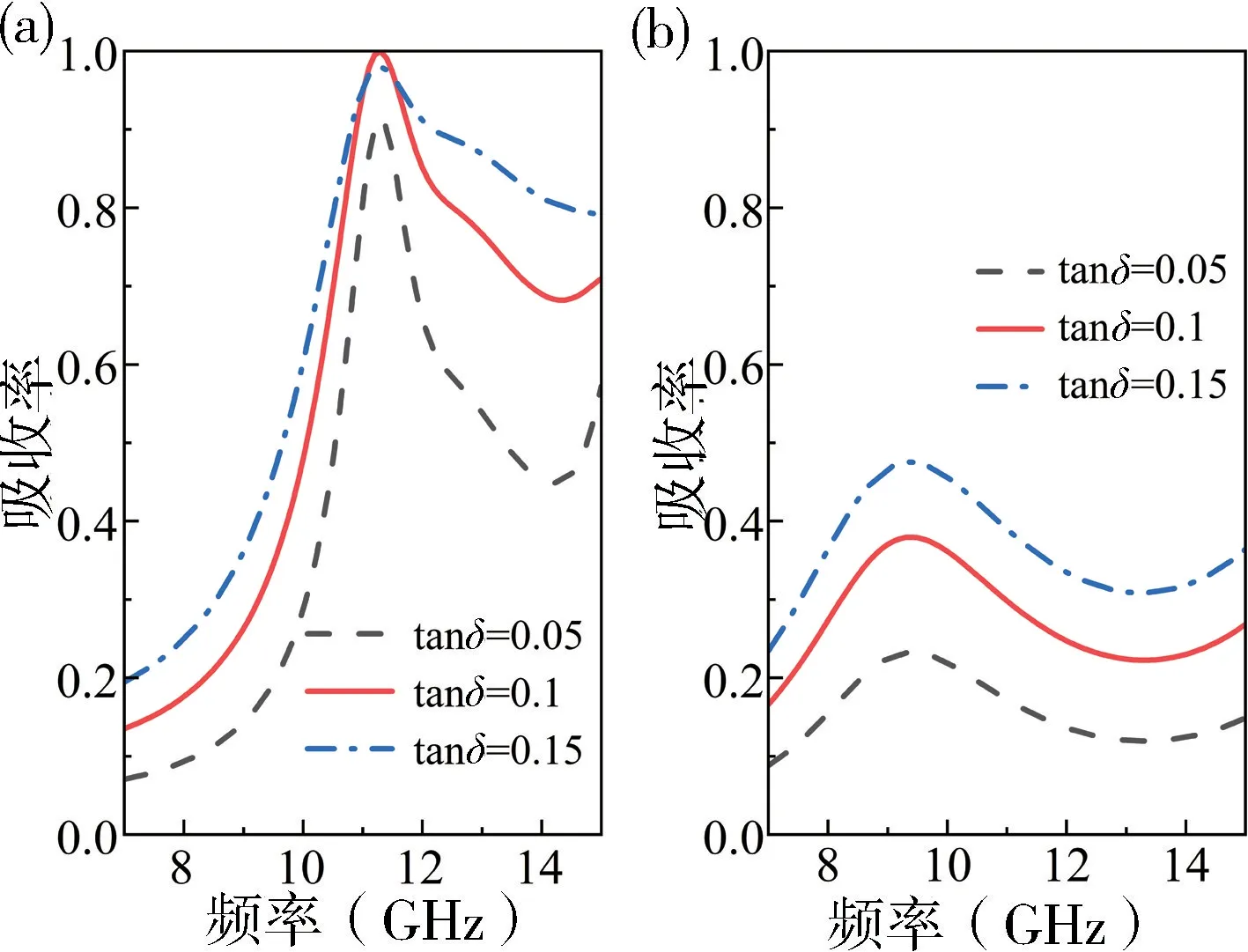
图3 (a)圆孔阵列超表面和(b)介质平板的吸收率随损耗角正切的变化Fig.3 The absorptivity of (a) circular hole array metasurface and (b) dielectric plate varies with the tangent of the dielectric loss angle

以上研究是5 mm 厚度介质板上分布周期性圆孔阵列实现完美吸收的情况,对于相同材料参数不同厚度的介质板,通过优化圆孔阵列的周期和直径,也能在其他频段实现完美吸收,从而实现完美吸收的连续可调谐性。图4 为厚度从3 mm 变化到7 mm 时完美吸收的圆孔直径D与谐振频率处的波长λ0的关系曲线。当厚度为3 mm,周期和直径分别优化为9.6 mm 和8 mm 时,在18.8 GHz(波长为16 mm)处实现完美吸收;当厚度为6 mm,周期和直径分别优化为19.2 mm和16 mm 时,在9.4 GHz(波长为32 mm)处实现完美吸收。因此在各自谐振频率处,圆孔直径与谐振波长的比值基本符合D/λ0=0.5 的关系,与Yang 等的文章报道结果[23]一致。

图4 不同厚度超表面实现完美吸收时直径与谐振波长的关系Fig.4 Diameter versus resonant wavelength for perfect absorption at different thicknesses of metasurface

上述研究都是基于电磁波的垂直入射(入射角为0°),对于斜入射的情况,研究结果如图5 所示。设置材料的介质损耗角正切值为0.1、超表面的周期为16 mm,通过优化圆孔直径和厚度,实现对超表面的完美吸收。由于超表面的单元结构具有中心对称性,所以只考虑入射角在0°～90°范围内的变化。当入射角为30°时,圆孔直径和厚度分别调整为14.4 mm 和4 mm,超表面的吸收率最大(98.1%),实现近完美吸收,如图5(a)所示。图5(b)和(c)给出了入射角分别为45°和60°的超表面最佳吸收情况。从图中可以看出,随入射角增大,吸收率将逐渐减小。

图5 入射角分别为(a)30°、(b)45°和(c)60°的吸收谱Fig.5 Absorption spectra with incidence angles of (a) 30°,(b) 45° and (c) 60°

2 实验案例

从以上电磁仿真研究结果可知,全介质超表面完美吸收需要两个基本条件,即超表面结构产生的电谐振模态和磁谐振模态发生简并且两个模态都处于临界耦合状态。然而,对于由同一种材料组分构成的介质基板而言,其材料的损耗难以与形成的谐振结构的辐射损耗刚好达到临界耦合。因此,本实验采用损耗极小的聚四氟乙烯陶瓷复合材料和损耗较大的磁性复合材料吸波片实现完美吸收。其中,聚四氟乙烯陶瓷复合材料的相对介电常数经测试为10,磁性复合材料吸波片由绵阳西磁科技有限公司生产,其相对介电常数和磁导率的测试结果如图6(a)所示。磁性复合材料吸波片覆盖在聚四氟乙烯陶瓷复合材料基板上得到的双层圆孔超表面单元结构如图6(b)所示,通过调节这两种材料的厚度,使双层基板组合达到简并临界耦合,进而实现完美吸收。

图6 (a)磁性复合材料吸波片的材料参数、介电常数的实部( ε′)和虚部( ε″)以及磁导率的实部( μ′)和虚部( μ″)随频率变化的曲线;(b)全介质超表面吸收器的单元结构,由上到下第一层为磁性吸波材料,第二层为聚四氟乙烯陶瓷复合材料Fig.6 (a) Material parameters of the magnetic composite absorber,the real ( ε′) and imaginary ( ε″) parts of the permittivity and the real ( μ′) and imaginary ( μ″) parts of the permeability as a function of frequency;(b) Unit structure of the all-dielectric metasurface absorber,from top to bottom the first layer is the magnetic absorbing material and the second layer is the Teflon ceramic composite

确定周期P=20 mm,圆孔直径D=17 mm,分别调节聚四氟乙烯陶瓷复合材料的厚度h1和磁性复合材料吸波片的厚度h2。考虑到双层圆孔结构的非对称性,需研究电磁波在不同端口入射时对吸收性能的影响。首先,考虑电磁波沿z轴方向入射(正入射)时的吸收情况: 图7(a)为磁性复合材料吸波片的厚度设置为1 mm,聚四氟乙烯陶瓷复合材料的厚度从3 mm 变化到5 mm 时的吸收谱。从图中可以看出,当h1=4 mm 时,超表面在10.3 GHz 处实现了完美吸收(99.6%);图7(b)为聚四氟乙烯陶瓷复合材料的厚度h1=4 mm,磁性复合材料吸波片的厚度从0.5 mm 变化到1.5 mm 时吸收曲线,从图中可以清楚地看出,当h2=1 mm 时超表面在10.3 GHz 处实现了完美吸收(99.6%)。所以,对于圆孔直径和圆孔周期固定的情况,可以通过调节聚四氟乙烯陶瓷复合材料和磁性复合材料吸波片的厚度实现双层介质结构的完美吸收。接着,考虑电磁波沿z轴负方向入射(反入射)时的吸收情况;图7(c)为磁性复合材料吸波片厚度为1 mm,聚四氟乙烯陶瓷复合材料的厚度在3～5 mm 变化过程中的吸收谱;图7(d)为聚四氟乙烯陶瓷复合材料的厚度为4 mm,磁性复合材料吸波片的厚度在0.5～1.5 mm 变化过程中的吸收谱。从这两幅图中可以看出,反入射时吸收率较低,所以仅仅通过调节聚四氟乙烯陶瓷复合材料和磁性复合材料吸波片的厚度无法实现完美吸收。

图7 周期P=20 mm,圆孔直径D=17 mm。电磁波正入射: (a) 磁性复合材料吸波片厚度为1 mm,聚四氟乙烯陶瓷复合材料厚度在3～4 mm 变化过程中的吸收谱;(b)聚四氟乙烯陶瓷复合材料厚度为4 mm,磁性复合材料吸波片厚度在0.5～1.5 mm 变化过程中的吸收谱;电磁波反入射: (c)磁性复合材料吸波片厚度为1 mm,聚四氟乙烯陶瓷复合材料厚度在3～4 mm 变化过程中的吸收谱;(d)聚四氟乙烯陶瓷复合材料厚度为4 mm,磁性复合材料吸波片厚度在0.5～1.5 mm 变化过程中的吸收谱Fig.7 Period P=20 mm,circular hole diameter D=17 mm.Electromagnetic wave forward incidence: (a) Absorption spectrum of magnetic composite absorbers with a thickness of 1 mm and teflon ceramic composite thickness varying from 3 mm to 4 mm;(b) Absorption spectrum of magnetic composite absorbers with a thickness of 4 mm and Teflon ceramic composite thickness varying from 0.5 mm to 1.5 mm;Electromagnetic wave back incidence: (c)Absorption spectrum of magnetic composite absorbers with a thickness of 1 mm and a thickness of teflon ceramic composite varying from 3 to 4 mm;(d) Absorption spectrum of teflon ceramic composite with a thickness of 4 mm and magnetic composite absorbers varying in thickness from 0.5 to 1.5 mm

图8(a)为单元结构在xy平面10×10 阵列的实验样品,对该样品进行的测试装置如图8(b)所示。在测试过程中,电磁波正入射的频率范围为6～18 GHz,测得的反射率、透射率和吸收率随频率变化的曲线如图8(c)所示。从图8(c)中可以看出,在9.68 GHz 处,吸收率的测量值达到了最大(92.4%),与仿真结果的差异主要是由于样品的尺寸较小而未能使谐振频率处入射波的透射率完全变为0 导致的。图8(d)为电磁波反入射的情况下实验和仿真结果,造成二者差异的原因与上述基本相同。因此,从两个实验结果来看,圆孔阵列全介质超表面具有接近完美吸收的吸波性能。

图8 (a)全介质超表面样品;(b)实验测试装置;电磁波(c)正入射和(d)反入射时吸收器的实验和仿真结果Fig.8 (a) All-dielectric metasurface sample;(b) Experimental test equipment;Experimental and simulation results of absorber at(c) forward and (d) reverse incidence of electromagnetic wave

3 结论

本文提出了一种双层圆孔阵列构建的全介质超表面完美吸收器。通过优化圆孔阵列几何参数,使超表面中激发的电谐振和磁谐振简并,再通过优化介质材料的损耗使材料损耗率等于辐射损耗率,进而实现超表面的完美吸收。采用厚度为1 mm 的磁性复合材料吸波片覆盖在厚度为4 mm 的聚四氟乙烯陶瓷复合材料上的双层介质结构,在其上排列周期为20 mm、直径为17 mm 的圆孔阵列时,能够在10.3 GHz 的频率处实现完美吸收。实验结果表明在9.68 GHz 处的吸收率为92.4%。仿真与实验结果的差异是由于样品的尺寸较小造成的。本文提出的双层圆孔阵列全介质超表面具有吸收效率高、结构简单、成本低等优点,有望在电磁隐身和屏蔽的应用中发挥重要应用。