出口宽高比对S 弯喷管流固耦合特性影响

李秋琳，周莉，孙鹏，史经纬，王占学

西北工业大学 动力与能源学院，西安 710129

在现代化战争中，为躲避精准制导武器的打击，隐身性成为第四代战机必备的性能，低可探测S 弯喷管是提高航空发动机排气系统隐身性能的关键技术之一。伴随着飞机长时间的高速飞行，S 弯喷管会持续在由气动载荷、热载荷以及结构载荷等组成的多物理场载荷环境下工作［1-2］。S 弯喷管的几何构型相比于传统的轴对称喷管更加复杂，特殊的几何构型使得喷管对于内部流动特征更加敏感，弹性特征更加突出，且复杂几何构型导致其内部流动呈现典型的非均匀特征，喷管壁面气动载荷分布十分复杂［3-4］。剧烈变化的气动载荷使得S 弯喷管出现复杂的变形特征，而S 弯喷管的变形特征反过来又会影响S 弯喷管的流动特性，从而改变喷管壁面的气动载荷分布。二者相互影响，从而形成S 弯喷管的流固耦合（也称“气动弹性”）作用［5-6］，导致S 弯喷管出现应力集中和结构大变形等复杂气动弹性现象，显著改变喷管的气动特性，严重影响S 弯喷管工作的稳定性以及战术性，给作战飞机带来不可估量的损害。

国内外研究人员针对多物理场载荷环境下的S 弯喷管结构变形与气动弹性问题开展了部分研究。Smith 和Dalenbring［7］针对“Eikon”隐身无人机所装备的S 弯喷管，采用双向松耦合方法开展了流固耦合数值研究，并针对S 弯喷管的气动变形机理及其抑制方法进行了分析和介绍。Nigam 等［8］利用ANSYS 有限元软件进行气动/热弹性结构分析，获得气动/热载荷作用下的排气系统结构响应特性，并对比压力载荷和温度载荷对排气系统结构变形特征的影响差异。Urbanczyk 等［9］发展了一套多物理场分析及设计优化软件COMANDO，采用单向气固耦合方法对两种不同结构支撑下的超声速二元喷管壁面厚度进行优化设计。Ma 等［10］建立了一种并行多尺度优化算法框架，并将其应用于复合平板和壳结构的材料分布优化，以实现约束条件下的结构固有频率最大化设计。孙鹏等［11］数值模拟了流固耦合作用下双涵道S 弯收敛喷管的结构变形特征及其内/外流特性，结果表明S 弯喷管在经历流固耦合作用后变形位置主要分布于第一弯下游壁面与喷管出口，导致喷管气动性能大幅降低。顾瑞等［12-13］基于MpCCI 耦合平台研究了不同几何调节位置对单边膨胀喷管流固耦合特性影响，分析了单边膨胀喷管的流固耦合振动特性，结果表明气固耦合作用对该模型推力性能的影响较小，但继续减小喷管唇口板的厚度会增大气固耦合作用对喷管整体性能的影响。

S 弯喷管的几何构型十分复杂，在设计过程中涉及的几何参数众多，这些参数对S 弯喷管的流动特性有着显著的影响。在实际的战机应用中，出口宽高比决定低可探测S 弯喷管的出口形状及其与飞机后机身的一体化构型，是设计过程中的重要参数之一［14］。Rao 等［15］针对3 种类型的单涵道S 弯收敛喷管，采用实验的方法对比分析了出口形状及弯曲流道对喷管内/外流特性的影响，结果表明弯曲构型及椭圆形出口导致喷管上/下壁面气流膨胀状态存在差异。Sun 等［16］数值研究了出口宽高比对单涵道双S 弯喷管气动性能与流动特性的影响，结果表明出口宽高比的差异会导致喷管内的气流局部加速、壁面压力分布不同，当落压比为2.4 时，随着宽高比由5 增加至15，推力系数降低了2.5%。矫丽颖等［17］研究了出口宽高比对与机身融合的S 弯喷管流动特性的影响，结果表明随着出口宽高比的增加，S 弯喷管尾喷流沿Y轴方向偏转幅度减小，沿Z轴方向偏转幅度增大。程稳［18］数值研究了出口宽高比对S弯喷管红外辐射特性的影响，结果表明S 弯喷管的燃气红外辐射强度随着出口宽高比增加而减小，总红外辐射强度平均降低10.8%。可见，出口宽高比这一关键几何参数对S 弯喷管气动性能和红外辐射特性产生显著影响。

综上所述，目前公开文献已关注到S 弯喷管多物理场下的结构响应特性，针对出口宽高比这一关键几何参数对S 弯喷管的影响研究则主要集中于气动和红外辐射特性，而关于粘性流动下的基于不同出口宽高比的双S 弯喷管流固耦合影响研究还未涉及，出口宽高比对流固耦合作用下的双S 弯喷管流动特性及气动性能的影响还未得到深入分析。因此，开展不同出口宽高比下的双S弯喷管双向流固耦合数值研究，分析出口宽高比这一关键几何参数对双S 弯喷管耦合特性影响及其流动特征影响，并进一步归纳出口宽高比对其气动性能和结构特征的影响规律，为同时满足结构强度可靠与气动性能较好的双S 弯喷管构型设计提供基础。

1 计算模型与数值方法

1.1 计算模型

本文研究的双S 弯喷管基准模型如图1 所示，喷管由混合室与S 弯段构成，喷管混合室基于某型涡扇发动机建立，包括波瓣混合器和尾锥。S 弯喷管通过型面遮挡发动机高温部件而实现红外隐身能力的提升，基于多参数耦合的变截面设计方法，通过喷管中心线变化规律设计、喷管沿程流通截面设计、低可探测设计准则的建立，实现不同构型的S 弯喷管设计。使用Lee 曲线进行中心线设计［19］，Lee 曲线包括“前缓后急”“均匀变化”“前急后缓”3 种变化规律。中心线的变化规律决定了双S 弯喷管两弯转弯处的曲率大小，曲率较大时将产生较大损失［14］，因此，选取“前急后缓-前急后缓”的两弯中心线变化规律。S 弯喷管的沿程流通截面由圆形进口截面渐变为二元出口截面，需在中心线上的各离散点处进行其截面参数计算与截面形状设计，根据已知的喷管进/出口截面形状及截面几何参数，求得沿程各截面的面积、宽度、高度等参数。低可探测设计准则的建立通过S 弯型面完全遮挡喷管进口前端的发动机高温部件，达到在任意探测角下均不可能被探测到高温部件，实现红外辐射强度的降低。

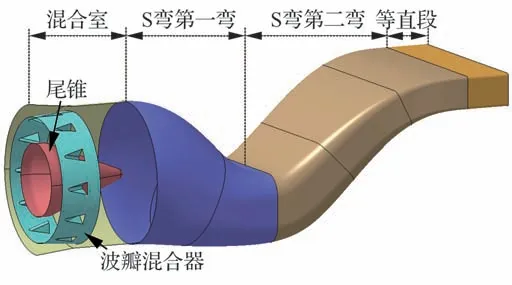
图1 双S 弯喷管基准模型Fig.1 Geometry model of double serpentine nozzle

图2 为S 弯段关键几何参数示意图，其中喷管入口面积Ain由喷管直径D确定，喷管直径D由混合室出口直径确定，喷管出口面积Ae根据发动机性能参数确定。S 弯喷管的主要设计参数包括：喷管直径D，喷管长度L，第一弯通道出口面积A1，第一弯出口宽高比W1/H1，第一弯通道轴向长度L1，第一弯纵向偏距ΔY1/L1；第二弯通道轴向长度L2，第二弯纵向偏距ΔY2/L2；喷管出口宽高比We/He，等直段长度L3。将L1和L2无量纲化为第二弯与第一弯长度比L2/L1，将L3无量纲化为等直段长度与直径比L3/D，主要几何设计参数取值如表1 所示。

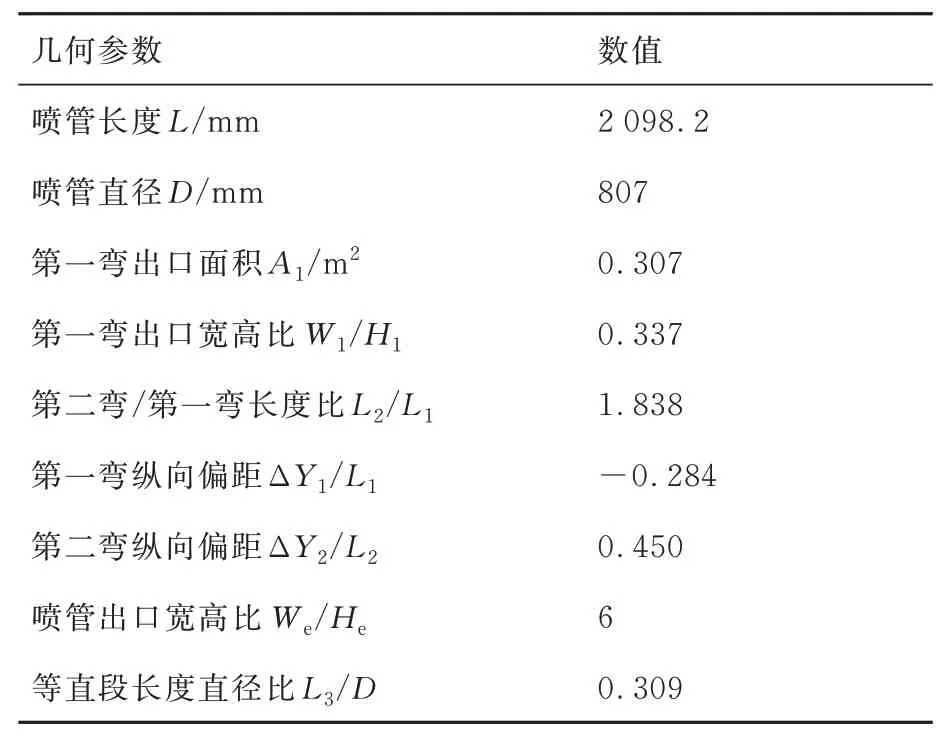
表1 主要几何设计参数取值Table 1 Design parameters of serpentine nozzle

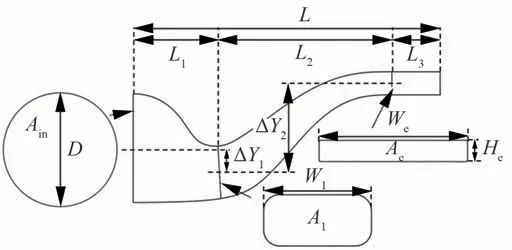
图2 S 弯段关键几何参数Fig.2 Design parameters of double serpentine nozzle

图3 中给出了S 弯喷管的完全遮挡高温部件的低可探测设计准则，即喷管上纵线和下纵线的公切线MN经过喷管出口上点C或喷管入口下点B，通过在喷管两弯（M、N两点）处的遮挡，对高温部件实现完全遮挡。S 弯喷管完全遮挡设计准则的实现与喷管进口直径、各弯轴向长度、等直段长度、各弯纵向偏距与第一弯出口宽高比、喷管出口宽高比直接相关，各参数之间存在相互耦合、相互制约的关系，尤其是第二弯偏距直接影响对高温部件的遮挡效果，通常S 弯喷管设计过程中，在给定相关设计参数取值后，基于公切线的低可探测设计准则而确定所需的第二弯偏距，以实现完全遮挡高温部件的目标。为了获得S 弯喷管关键设计参数——出口宽高比对其流固耦合特性的影响，其他设计参数保持不变，按照文献［14］的研究结果进行选取，此时，在S 弯喷管完全遮挡高温部件的低可探测设计准则约束下，出口宽高比仅与第二弯偏距相关联，当喷管出口宽高比改变时，喷管第二弯偏距将随着出口宽高比的增加而减小。

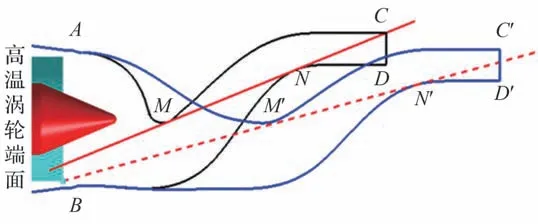
图3 完全遮挡高温部件的低可探测设计准则Fig.3 Low detectability design criteria to completely shield high temperature components

图4 为双S 弯喷管的流固耦合模型示意图。喷管外为自由来流，内流为经过混合室后的掺混气流。在内/外流气动载荷的共同作用下，S 弯喷管会发生结构变形。喷管的内壁面、外壁面及出口壁面共同组成流固耦合面，用于进行气动载荷与变形数据的交换。喷管内/外流及流固耦合面组成S 弯喷管流固耦合计算模型的流体域，喷管固体壁面及流固耦合面组成S 弯喷管流固耦合计算模型的固体域。

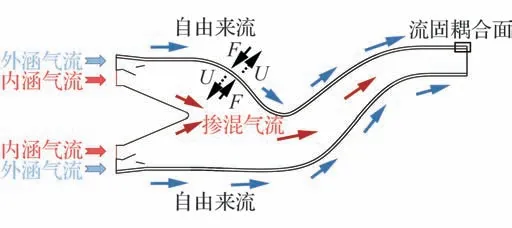
图4 双S 弯喷管的流固耦合模型Fig.4 Fluid-structure interaction model of double serpentine nozzle

1.2 数值方法

S 弯喷管流体域的数值模拟采用计算流体动力学（Computational Fluid Dynamics，CFD）软件Fluent 进行数值仿真，采用压力基求解三维非定常可压缩雷诺平均Navier-Stokes（N-S）方程，湍流模型选择剪应力运输（Shear Stress Transpert， SST）k-ω模型，空间离散采用二阶迎风格式，工质为理想气体。S 弯喷管固体域采用（Computational Structural Dynamics，CSD）软件Abaqus 进行计算，固体域的结构分析采用有限单元法，基于Newmark-β直接积分法在时域上求解结构动力学方程，求解采用动态隐式分析步。

S 弯喷管流体域的计算网格及边界条件如图5 所示，计算域包括喷管域和远场域，采用ICEM 软件对S 弯喷管的全三维流场进行网格划分，计算域采用混合网格拼接而成。由于S 弯喷管壁面在流固耦合作用下发生结构变形，因此将喷管域设置为动域，采用四面体非结构网格划分以满足动网格光顺及重构［19］要求，其中近壁面网格进行加密处理以满足SSTk-ω湍流模型的计算要求。由于S 弯喷管出口下游的远场域未发生变形，因此将远场域设置为静域，采用六面体结构网格划分。经过网格无关性验证，计算所采用的网格为538 万。S 弯喷管固体域的结构模型采用六面体网格划分，固体域有限元模型如图6 所示，其中网格单元类型为8 节点线性非协调模式单元。经过网格无关性验证，计算所采用的网格数量为80 664。

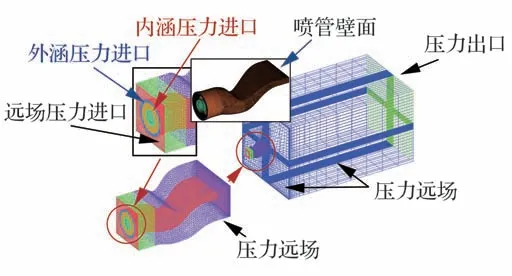
图5 计算网格及边界条件Fig.5 Numerical grid and boundary condition

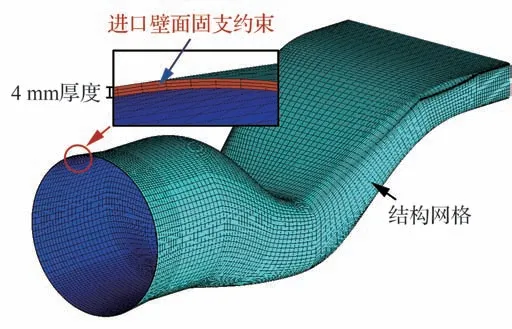
图6 固体域有限元模型Fig.6 Finite element model of solid domain

非定常流场的计算工况为地面工况，环境压力为101 325 Pa，环境温度为288 K。内/外涵进口采用压力进口边界，外涵进口落压比P/Pb为2.782，进口总温为987.2 K；内涵进口落压比P/Pb为2.714，进口总温为412.7 K，进口来流沿轴向方向，喷管壁面采用无滑移绝热壁面。远场静域出口设置为压力出口边界，出口压力为101 325 Pa，出口温度为288 K，喷管动域和远场静域的其他边界均设置为远场边界。

在结构场中，S 弯喷管被假设为悬臂梁结构，进口面采用固支约束，喷管壁面厚度为4 mm。S弯喷管结构材料选用GH706 高温合金，材料属性包括弹性模量E、密度ρ以及泊松比μ，具体参数值如表2 所示。基于瑞利阻尼假设［20］设置较大的结构阻尼以消除喷管可能出现的结构振动。

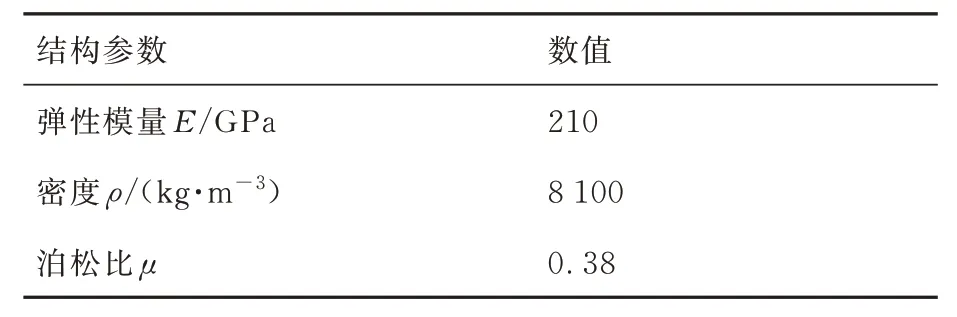
表2 固体材料属性Table 2 Physical properties of solid material

2 耦合求解方法与校核

2.1 耦合求解方法

综合考虑求解精度与计算资源，在流固耦合数值方法上采用串行双向松耦合算法［21］，计算过程如图7 所示。采用MpCCI（Mesh-based parallel Code Coupling Interface）作为流体域和固体域数据的耦合交换平台，实现流体域计算得到的气动载荷F以及固体域计算得到的变形位移U在流固耦合面上的相互传递。其中，气动载荷F包括流动产生的压力与黏性力。流/固求解器空间离散方式的差异导致耦合面两侧的流体网格与变形后的固体网格的形状及尺寸难以在空间上完全对应。采用局部插值法进行两场之间的数据差值传递，基于MpCCI 平台采用“关联-插值”的方式对耦合区域两侧的流场网格和结构网格进行快速匹配。此外，变形后的流场/结构耦合边界上需要满足位移协调条件与力平衡条件，如式（1）和式（2）所示：

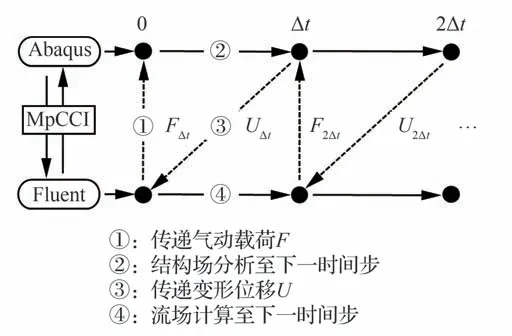
图7 串行双向松耦合算法计算过程Fig.7 Solution mechanism of series two-way loosely coupled algorithm

式中：Us和Uf分别表示耦合界面上相互关联的结构场/流场网格的节点位移；Ff表示耦合界面上的气动载荷，是气流压力pf和气流黏性力σf之和；σs表示耦合界面上的结构应力；nf和ns分别表示耦合界面上流场侧和结构侧的法向向量。

在耦合求解开始时，首先从Fluent 获取给定边界条件下的流体域定常解。根据串行策略，在每个时间步内，首先将流体域计算得到的气动载荷通过耦合面传递给固体域，Abaqus 依据接收的气动载荷完成结构分析后，将得到的变形位移数据通过耦合面传递给流体域，此时Fluent 推进至下一个时间步，根据新的流动边界完成下一个时间步内的流场求解，在每个计算时间步内分别求解流体域与固体域的控制方程。由于存在时间步滞后以及耦合界面上能量的不完全守恒，串行双向松耦合方法为一阶时间精度，因此耦合过程中需要使用较小的时间步来保证计算的稳定性与准确性。

2.2 耦合时间步验证

流固耦合模拟必须设置较为合理的时间步以保证计算的稳定性和准确性。在S 弯喷管流体域与固体域网格满足无关性条件的基础上，选取3 组不同耦合时间步长Δt1=1 ms、Δt2=2 ms 以及Δt3=4 ms［22-23］进行流固耦合数值计算。当喷管结构变形达到稳定状态时，不同时间步长下的S 弯喷管第一弯下游上壁面最大变形量及误差值如表3 所示。时间步长Δt2=2 ms 以及Δt3=4 ms计算得到的喷管第一弯下游上壁面变形量误差为1.84%；而时间步长Δt1=1 ms 和Δt2=2 ms 计算得到的喷管第一弯下游上壁面变形量误差仅为0.77%。因此，采用时间步长Δt2=2 ms 能够在加快计算速度的基础上较为准确地模拟S 弯喷管的流固耦合特性。

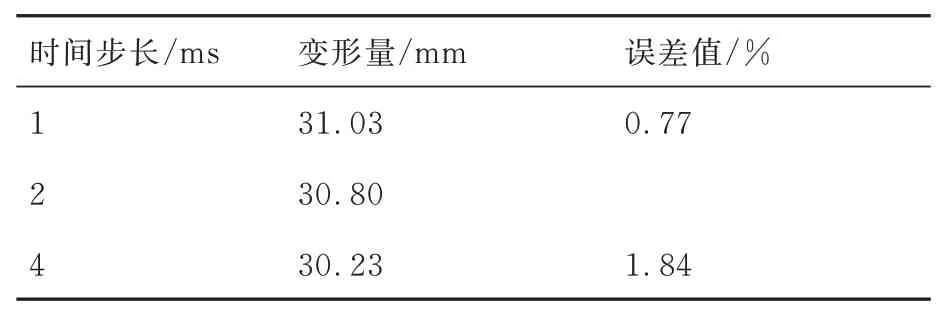
表3 耦合时间步验证结果Table 3 Coupling time step verification results

2.3 耦合方法校核

为了验证本文所采用的串行双向松耦合算法及MpCCI 耦合平台的数值精度，开展了双S弯喷管缩比模型的冷态实验研究。为了测量流固耦合下的S 弯喷管缩比模型的气动变形特征，采用VIC-3D（Video Image Correlation-3D）非接触全场应变分析测量系统，通过壁面喷涂测量散斑并确定变形前/后图像中对应散斑像点之间的位置坐标关系，获取S 弯喷管壁面关键部位的变形位移分布，变形位移的测量精度为0.01 mm。

S 弯喷管缩比实验模型为文中所研究双S 弯基准喷管的10∶1 缩比模型，采用sla 光敏树脂作为结构材料，实验模型的壁面厚度为1.6 mm，S弯喷管实验模型及其壁面喷涂测量散斑效果如图8 所示。此外，为了有效抑制S 弯喷管结构的振动响应，实验模型在S 弯喷管缩比模型的基础上将喷管出口等直段上壁面的厚度增加至3.2 mm。实验边界采用地面工况，喷管外涵进口落压比为1.71，内涵进口落压比为1.63，内外涵进口总温为288 K。

图8 S 弯喷管实验模型及壁面喷涂测量散斑效果Fig.8 Experimental model of serpentine nozzle and wall spraying for scattering effects measurement

对比分析了S 弯喷管壁面变形位移分布及对称面壁面轮廓的数值模拟结果与实验测量数据，S 弯喷管上、下壁面变形位移的对比如图9 所示。由图9 可知，流固耦合数值计算获得的喷管上、下壁面的关键变形特征及其分布位置均与实验结果基本一致，主要表现为第一弯通道局部“鼓包”以及喷管等直段沿Y向向上偏移。数值模拟结果与实验测量数据的主要差异位于喷管出口位置，实验测量得到喷管出口上、下壁面的Y向变形位移值均略大于数值预测结果。

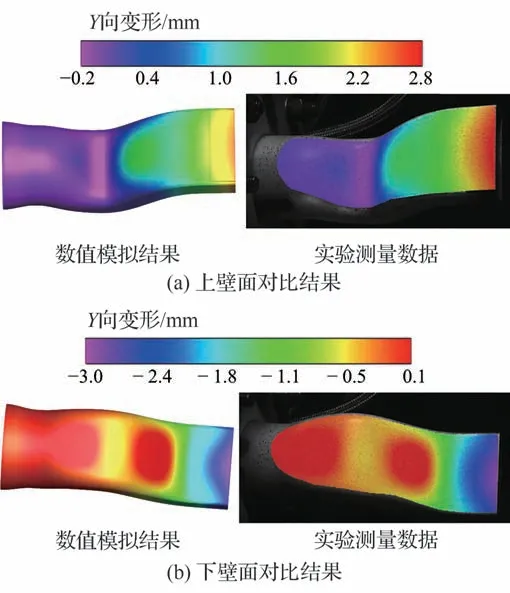
图9 变形位移的数值预测与实验数据对比Fig.9 Comparison of displacement between numerical simulation and experiment

图10 对比了S 弯喷管模型对称面内壁面轮廓的数值模拟结果与实验测量数据，表4 给出了S 弯喷管模型对称面轮廓误差。数值预测值与实验测量值误差较大的区域主要位于第一弯下游通道上壁面及喷管出口位置，第一弯下游通道上壁面位置的最大相对误差值为9.0%，喷管出口上壁面的相对误差最大值为8.8%，喷管出口下壁面的最大相对误差值为9.1%。与国内外不同类型喷管的数值/实验误差相比［22-23］，其中文献［22］中平均误差20%，文献［23］中最小误差7%，而本文的数值模拟结果与实验测量数据误差值较小，是合理可靠的。综上所述，串行双向松耦合算法能够准确地模拟双S 弯喷管的流场特征及结构变形特征。

表4 对称面轮廓误差Table 4 Contour error values of symmetric surface

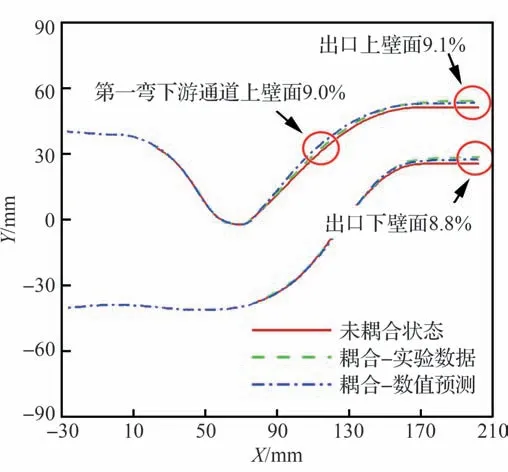
图10 S 弯喷管模型对称面轮廓的数值预测与实验数据对比Fig.10 Comparison of wall profiles on symmetry plane between numerical simulation and experiment

3 结果与分析

3.1 不同出口宽高比下喷管变形特征

在地面工况下，研究了8 种不同出口宽高比（We/He）参数对S 弯喷管双向流固耦合特性的影响。不同出口宽高比S 弯喷管的几何构型如图11 所示，出口宽高比及相应的第二弯无量纲纵向偏距的取值如表5 所示，在满足完全遮挡高温部件的设计准则下，第二弯无量纲纵向偏距发生变化，其它几何参数按照文献［14］的研究结果进行选取，均为设计状态下的值。第二弯无量纲纵向偏距反映了S 弯喷管纵向转弯处的弯曲曲率大小，当喷管出口宽高比增加时第二弯纵向偏距逐渐变小，喷管型面的横向扩张范围增大，从而使得S 弯喷管沿纵向方向的型面弯曲曲率逐渐减小，沿横向方向的型面弯曲曲率逐渐增大。因此，随着出口宽高比的增加，整个S 弯喷管几何构型沿纵向的弯曲流道变得更为平缓，沿横向的扩张角度逐渐增大。

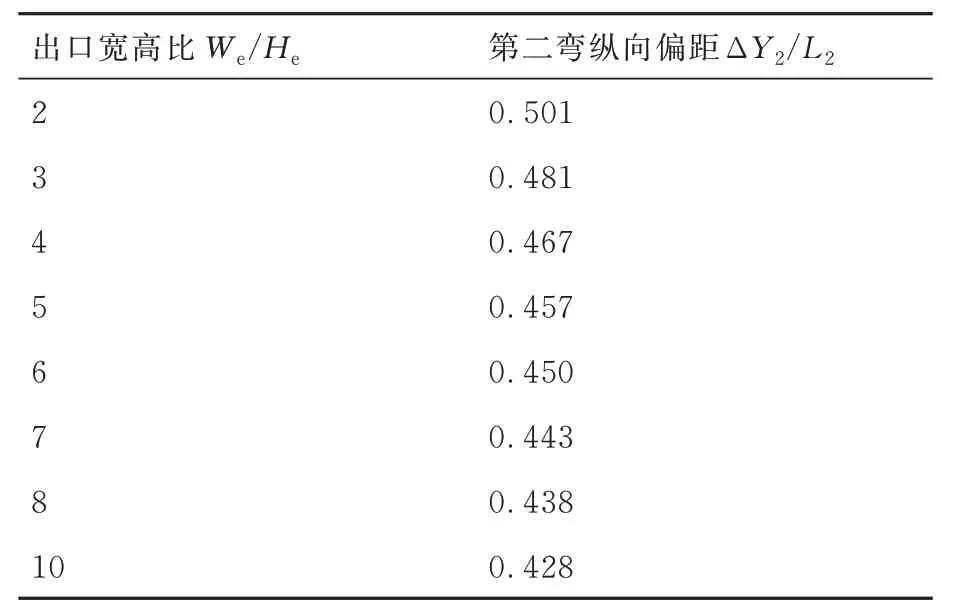
表5 S 弯喷管出口宽高比及对应的第二弯纵向偏距取值Table 5 Values of longitudinal offset distance of the second bend at different aspect ratios for serpentine nozzle

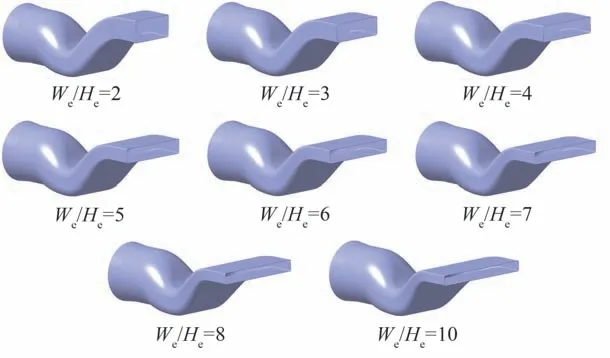
图11 S 弯喷管几何构型Fig.11 Serpentine nozzle geometries

由于S 弯喷管的复杂几何构型所造成的非均匀气动载荷与弹性体结构造成的复杂的变形特征相互影响，形成了S 弯喷管的流固耦合作用。当S 弯喷管的流固耦合作用达到动态平衡时，其结构变形特征开始保持稳定。由图9 和图10 可知，由于受到S 弯弯曲构型的影响，S 弯喷管的结构变形主要分布于S 弯喷管上下壁面，由于侧壁面构型无较大曲率的弯曲结构，因此S 弯喷管侧壁面变形量较小。其中，S 弯喷管上下壁面变形主要表现为S 弯第一弯下游通道的壁面膨胀变形和喷管等直段出口沿Y方向向上的弯曲变形。

图12 给出了耦合状态下不同出口宽高比S弯喷管上壁面的变形量分布。由图12 可知，不同宽高比的S 弯喷管上壁面变形主要集中在S 弯喷管第一弯下游区域及喷管等直段出口区域。对于S 弯喷管第一弯下游区域，随着出口宽高比的增加，S 弯喷管第一弯下游区域上壁面变形量逐渐增大。当出口宽高比为2 时，S 弯喷管第一弯下游区域变形量局部最大值为18.7 mm；当出口宽高比增加至10 时，S 弯喷管第一弯下游区域变形量局部最大值增加至39.5 mm。对于喷管等直段出口区域，随着出口宽高比的增加，喷管出口的变形量先增大后减小，在出口宽高比为6 时达到最大。当出口宽高比为2 时，喷管出口变形量局部最大值为17.0 mm；当出口宽高比增加至6 时，喷管出口变形量局部最大值增加至30.5 mm；当出口宽高比增加至10 时，喷管出口局部变形量减小至24.9 mm。随着出口宽高比的增加，喷管上壁面的变形分布范围逐步扩大，但分布位置无较大差异。

图12 S 弯喷管的上壁面变形量分布Fig.12 Displacement contours of upper wall of serpentine nozzle

图13 给出了耦合状态下不同出口宽高比S弯喷管下壁面的变形量分布。由图可知，不同出口宽高比的S 弯喷管下壁面变形主要集中在S 弯喷管第一弯下游区域，喷管等直段出口在下壁面区域无明显变形。随着出口宽高比的增加，S 弯喷管第一弯下游区域下壁面变形量逐渐增大。当出口宽高比为2 时，S 弯喷管第一弯下游区域变形量局部最大值为19.7 mm；当出口宽高比增加至10 时，S 弯喷管第一弯下游区域变形量局部最大值增加至36.5 mm。随着出口宽高比的增加，喷管上壁面的变形分布范围逐步扩大，但分布位置无较大差异。综合图12 与图13 可得，当出口宽高比＜6 时，S 弯喷管最大变形量出现在第一弯下游下壁面；当出口宽高比＞6 时，S 弯喷管最大变形量出现在第一弯下游上壁面，上下壁面最大变形量差值较小。

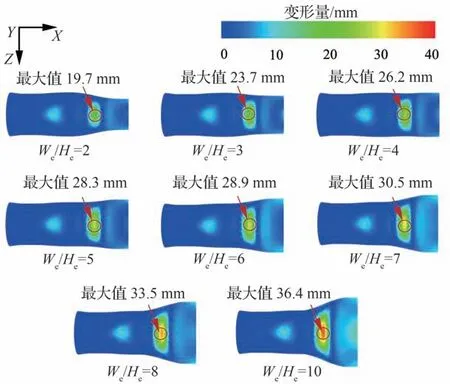
图13 S 弯喷管的下壁面变形量分布Fig.13 Displacement contours of lower wall of serpentine nozzle

当流固耦合作用达到动态平衡后，S 弯喷管出口截面长边向外膨胀，导致喷管的实际宽高比在耦合作用下相比设计宽高比均减小。表6 中给出了设计宽高比与实际耦合作用下的出口宽高比，图14 中给出了不同出口宽高比喷管出口截面轮廓图。出口截面在流固耦合作用下导致的变形程度可以反映在宽高比的变化率上，出口宽高比的变化率随着宽高比增加先增大后减小，这表示气流与喷管等直段出口结构的相互作用并不随着宽高比增加、出口形状逐渐扁平化而增强，这是由于喷管第二弯偏距减小所导致的出口弯矩减小，气动载荷对喷管出口作用因此减小，综合出口截面构型变化最终导致出口壁面变形先增大后减小，因此变化率随宽高比增加先增大后减小。

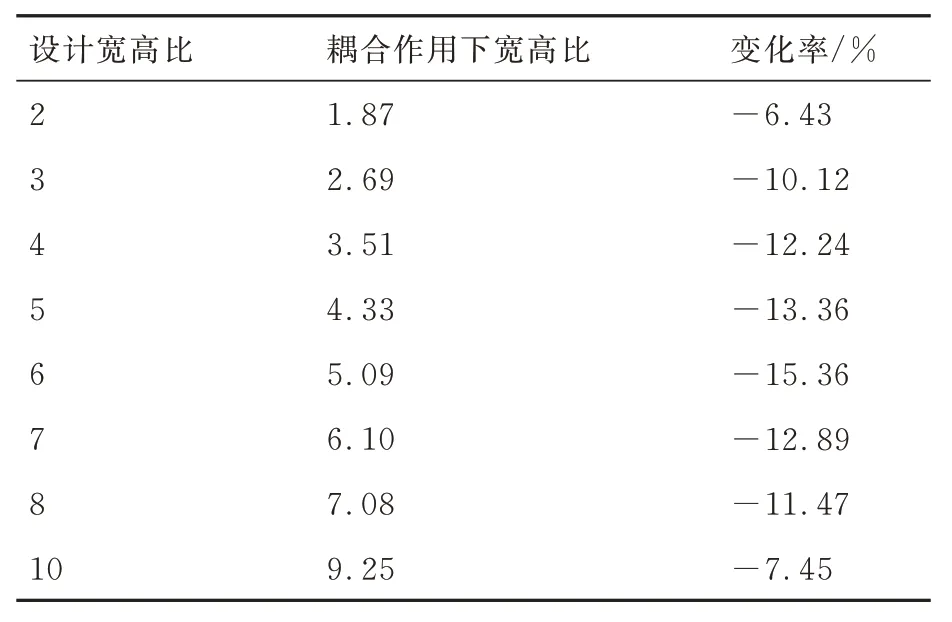
表6 喷管设计出口宽高比与耦合作用下出口宽高比数值Table 6 Design exit width to height ratio and coupled exit width to height ratio values

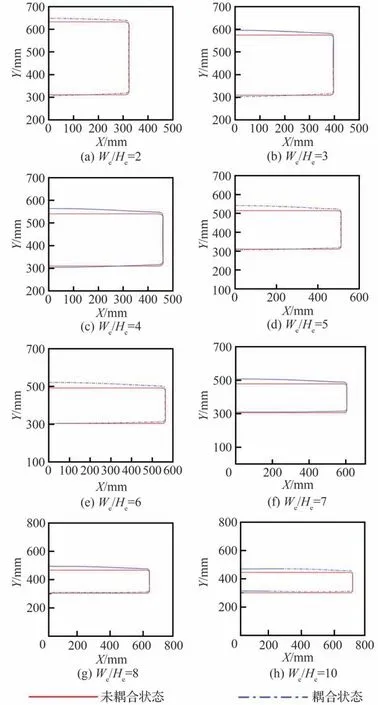
图14 喷管出口截面轮廓Fig.14 Profile of nozzle outlet section

S 弯第一弯下游通道壁面变形主要受到S 弯圆转方构型以及第一弯下游通道矩形截面的影响，随着宽高比增加，第一弯通道形状逐渐趋于“扁平”，通道侧壁面受到的气动载荷减弱，通道上下壁面受到的气动载荷增强，增强了喷管第一弯通道几何构型的不稳定性，因此喷管第一弯壁面变形量逐渐增大。S 弯等直段出口壁面变形主要受到S 弯喷管弯曲构型以及出口通道矩形构型的影响，随着宽高比增加，第二弯纵向偏距逐渐变小，弯曲程度减小，局部气动载荷减小，这导致S 弯第二弯的弯曲构型对喷管出口变形的影响随着宽高比增加逐渐减弱；同时，等直段出口通道形状逐渐趋于“扁平”，增强了喷管出口的何构型的不稳定性，相反地，这导致出口通道矩形构型对喷管出口变形的影响随着宽高比增加逐渐增强，2 种效果相互叠加，导致喷管出口壁面变形量随着出口宽高比增加而先增加后减小，出口宽高比的变化率随着宽高比增加先增大后减小，在出口宽高比为6 时达到最大。

综上可得，S 弯喷管的最大变形在8 种出口宽高比范围内均出现在S 弯第一弯下游区域，壁面“鼓包”特征更为显著，等直段的弯曲程度先增大后减小，相比喷管等直段，S 弯第一弯下游通道更易受到气动载荷造成的结构变形作用。且随着出口宽高比的增加，S 弯喷管壁面的变形分布范围逐步扩大，但分布位置无较大差异。

3.2 不同出口宽高比下喷管气动性能

对8 种不同出口宽高比的双S 弯喷管在流固耦合作用前后的气动性能结果进行了统计分析，图15 对比了不同出口宽高比下的S 弯喷管气动性能。在未耦合状态下，随着出口宽高比的增加，总压恢复系数、流量系数在出口宽高比为2～3 时增加，随后呈下降趋势，而推力系数随着出口宽高比的增加而减小，但变化程度较小。在耦合状态下，总压恢复系数、流量系数及推力系数相比未耦合状态均大幅降低，总压恢复系数降低了0.56%，流量系数降低了2.67%，推力系数降低了0.72%。当出口宽高比＞2 时，随着出口宽高比的增加，S 弯喷管的总压恢复系数、流量系数及推力系数降低，且随着宽高比的增加，流固耦合作用所造成的气动性能变化逐渐增大，在出口宽高比为10 时达到最大，此时总压恢复系数降低了0.36%，流量系数降低了4.34%，推力系数降低了1.37%。

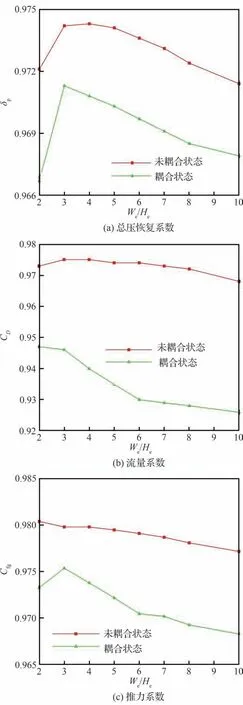
图15 S 弯喷管气动性能对比Fig.15 Comparisons of aerodynamic performance of serpentine nozzle

为了分析不同出口宽高比下的S 弯喷管气动性能在耦合作用前后的变化原因，首先分析S 弯喷管内部的流动特征。图16 给出了不同出口宽高比的S 弯喷管对称壁面静压分布。选取出口宽高比为2、4、6、8 和10 的情况进行分析，其中P/Pb为壁面静压与环境压力的无量纲比值；x/L为喷管横坐标与喷管长度的无量纲比值。在未耦合状态下，随着出口宽高比的增加，S 弯喷管第一弯附近的上壁面静压逐渐增大，这是由于出口宽高比的增加导致第二弯纵向偏距减小，喷管第一弯转弯处的纵向曲率降低，气流加速程度减弱，静压升高。喷管第二弯附近的下壁面静压随着宽高比的增加先增大，到出口宽高比6 时减小。在耦合状态下，第一弯下游通道中间区域的上、下壁面向外侧鼓起导致喷管流道出现局部的扩张-收缩特征。当宽高比为2 时，由于第一弯转弯处曲率过大，在下游产生了较大的逆压梯度，从而导致了严重的流动分离，此流动分离向上游传递使喷管第一弯转弯处的马赫数减小，壁面静压增大。当宽高比＞2 时，气流未出现明显的流动分离特征，由于第一弯下游壁面局部膨胀变形的影响，在此区域气流加速程度大于未耦合状态，因此第一弯处静压有所降低。随着出口宽高比的增加，S 弯喷管的对称面静压均表现为通过增大下壁面的弯曲曲率导致第二弯转弯处的下壁面静压大幅降低。

图16 S 弯喷管对称壁面静压分布Fig.16 Comparisons of static pressure distribution contours inside serpentine nozzle

S 弯喷管的气动性能主要由喷管内部流场产生的沿程摩擦损失、局部加速损失及掺混损失决定［24］。为了明确不同出口宽高比下的S 弯喷管内各项损失的变化，图17 给出了不同宽高比S 弯喷管的壁面剪切应力分布。结合图16，在未耦合状态下，随着出口宽高比的增加，喷管沿流向横截面逐渐“扁平”化，第一弯处气流加速效果减弱，剪切应力逐渐减小，喷管第二弯处气流加速效果增强，剪切应力随着宽高比增加逐渐增大，在喷管等直段达到最大，摩擦损失增加。在耦合状态下，当出口宽高比为2 时，第一弯下游的流动分离导致第一弯转弯处出现低速区，剪切应力减小，该区域内摩擦损失降低。此外，由于喷管壁面的膨胀变形，导致喷管湿周面积的增加，因此整体摩擦损失增加。当出口宽高比＞2 时，流固耦合作用导致喷管第一弯转弯处气流加速效果增强，剪切应力相比未耦合状态增大，摩擦损失增加。流固耦合作用对喷管第二弯至出口壁面剪切应力无明显影响，因此其特征与未耦合状态相似。喷管的变形量随着宽高比增加逐渐增大，湿周面积增大造成摩擦损失随着宽高比增加而增大。在2 种原因的共同作用下，S 弯喷管的摩擦损失随着宽高比增加而增大，由摩擦损失所造成的气动性能变化逐渐增大。

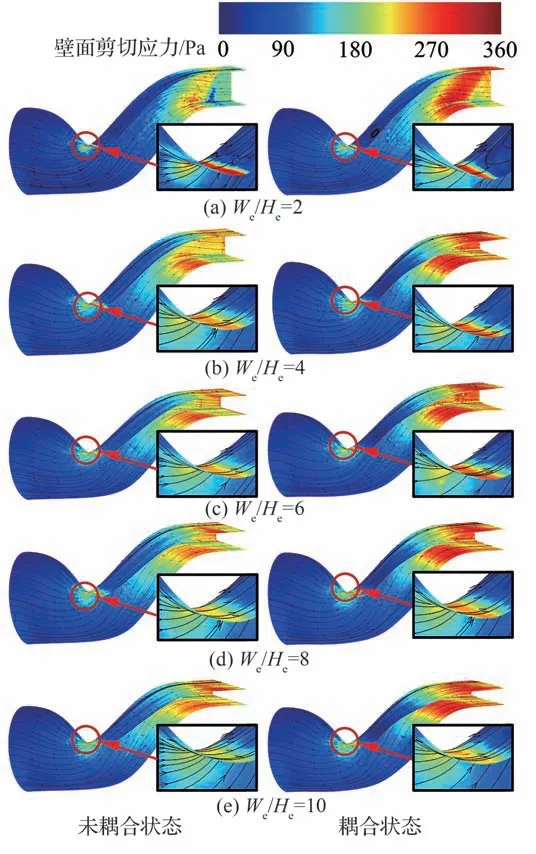
图17 S 弯喷管的壁面剪切应力分布Fig.17 Comparisons of wall shear contours inside serpentine nozzle

为了更加具体地分析流固耦合作用对不同出口宽高比的S 弯喷管气动性能的影响与性能变化原因，图18 给出了S 弯喷管沿程截面的无量纲轴向位置，其中：截面A 为混合室出口截面即喷管入口截面；截面B 位于喷管入口与第一弯转弯处之间；截面C 位于第一弯转弯处；截面D 位于第一弯转弯处与第二弯转弯处之间；截面E 位于第二弯转弯处；截面F 为等直段进口截面；截面G为喷管出口截面。取S 弯喷管型面的弯曲方向为Y 轴方向，且向上为正方向。

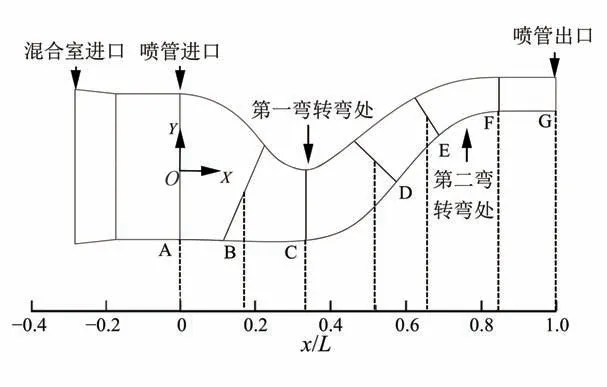
图18 S 弯喷管沿程截面的无量纲轴向位置Fig.18 Streamwise locations of cross sections inside serpentine nozzle

图19 给出了不同出口宽高比下的S 弯喷管沿程截面上的马赫数分布。在未耦合状态下，随着出口宽高比的增加，喷管第一弯转弯处曲率降低，截面C 的马赫数减小，局部加速损失减小。当出口宽高比增加时，喷管沿纵向收缩变强，气流加速至超声速，截面F 与截面G 的马赫数分布随着宽高比增加先减小后增大，在宽高比6 时最小。在耦合状态下，当出口宽高比为2 时，流动分离在截面D 与截面E 上表现为出现显著低速区，流动损失增大，截面E 的马赫数已达到局部超声速，局部加速损失增加。当宽高比＞2 时，截面C 及其下游截面马赫数随着宽高比增加而减小，且均在喷管通道内达到局部超声速，表现为截面D 至喷管出口马赫数增加，在截面E 上达到超声速。截面D 与截面E 的马赫数随着出口宽高比增加而减小，第二弯出口下壁面的局部加速损失减小，由局部加速损失所造成的气动性能变化逐渐减小。

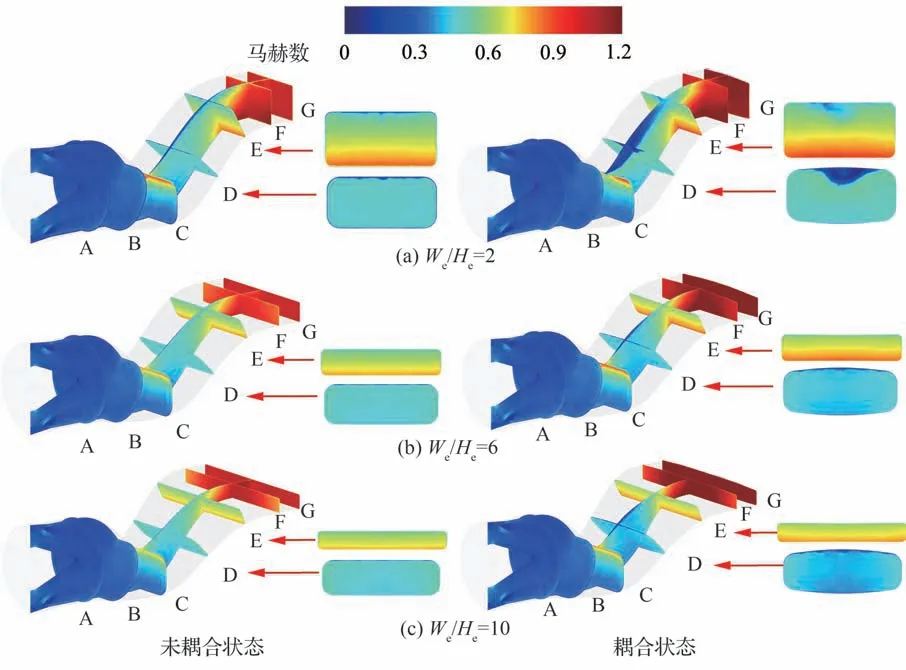
图19 S 弯喷管沿程截面上的马赫数分布Fig.19 Comparisons of Mach numbers on cross sections inside serpentine nozzle

图20 给出了不同出口宽高比的S 弯喷管沿程截面上的X方向涡量分布。在未耦合状态下，出口宽高比的差异引起的喷管下游流场扰动对上游附近的流动特征影响较小，因此不同出口宽高比下的喷管上游涡量分布基本一致，表现为截面A、截面B 与截面C 上的涡量分布基本一致。从截面C 至截面G 的涡量减小，掺混损失减小。在耦合状态下，当出口宽高比为2 时，喷管变形导致截面D 与截面E 附近的流道曲率增大，表现为气流转弯后在第二弯通道的截面D 上侧出现明显的气流分离区，截面E 中间上部分的流向涡合并，涡量显著增强，此时喷管内的掺混损失大幅增加；随着气流向后移动，上壁面涡量被拉伸，逐渐向侧壁面移动。相比未耦合状态，涡量显著增强。当出口宽高比＞2 时，喷管气动载荷所造成的结构变形并未引起喷管第一弯下游的流动分离，涡量相比未耦合状态未出现明显变化，且各个宽高比下涡量几乎相同，不因宽高比改变有较大变化，因此在出口宽高比＞2 时掺混损失相近。综上所述，随着出口宽高比增加，流固耦合作用带来的掺混损失先增大后趋于不变，由掺混损失所造成的气动性能变化逐渐减小。

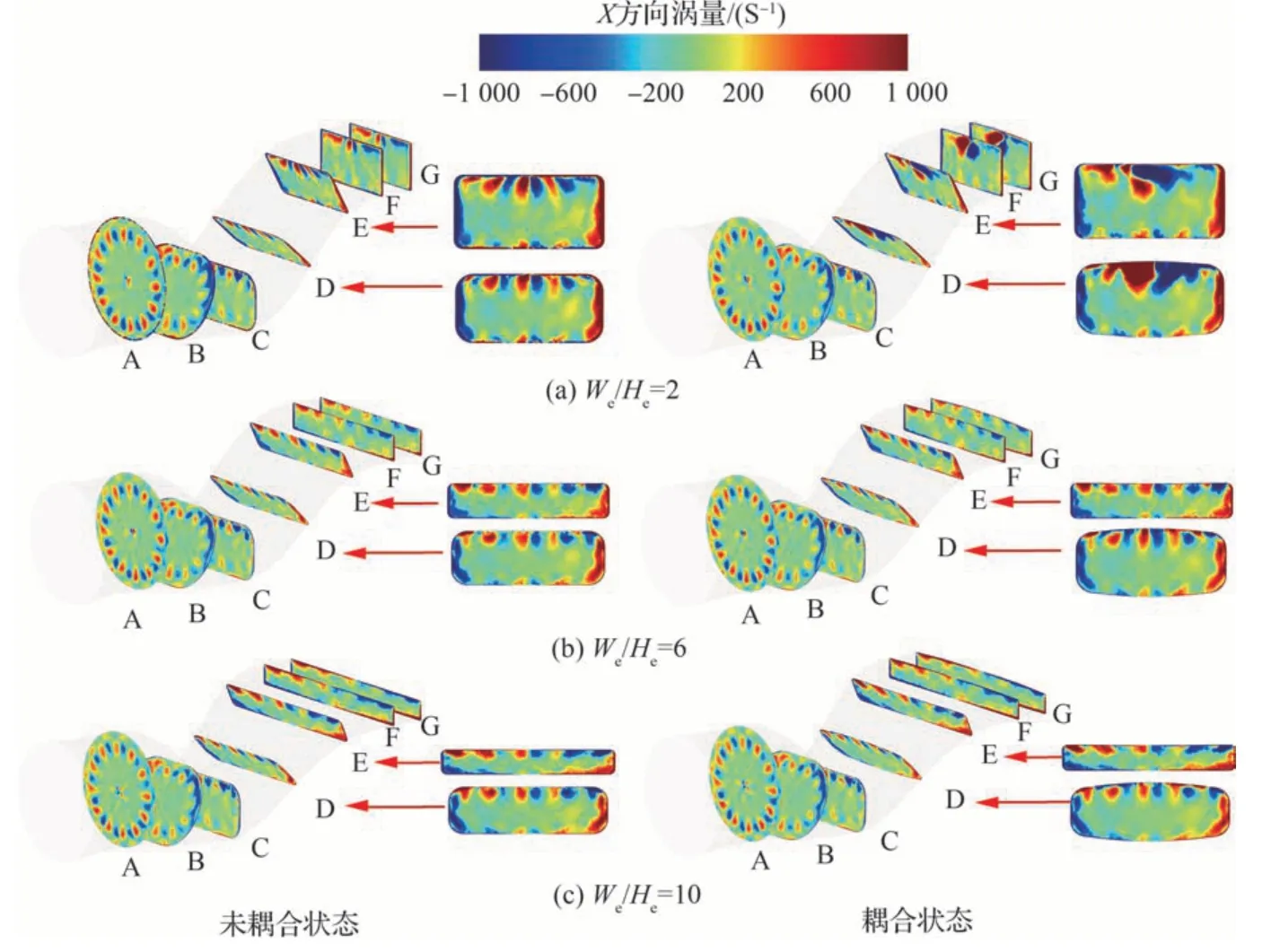
图20 S 弯喷管沿程截面上的X 方向涡量分布Fig.20 Comparisons of X vorticities on cross sections inside serpentine nozzle

图21 给出了不同出口宽高比S 弯喷管出口的推力矢量角。在未耦合状态下，喷管出口推力矢量角接近0°，尾喷流沿水平方向喷出。在耦合状态下，喷管出口段结构在气动载荷作用下沿纵向向上弯曲，尾喷流均沿轴向向上偏转。当宽高比为2～3 时，喷管出口推力矢量角随出口宽高比增加而减小；当宽高比＞3 时，喷管出口推力矢量角随出口宽高比增加而增大。结合总压恢复系数与推力矢量角的变化，推力系数降低，且变化率逐渐增大。

图21 S 弯喷管出口推力矢量角Fig.21 Thrust vector angle of serpentine nozzle exit

根据上述分析，在流固耦合作用下，第一弯下游通道气流的摩擦损失增大，局部加速损失增大。当出口宽高比为2 时，由流动分离造成较大的掺混损失，总压恢复系数与流量系数大幅降低。当出口宽高比＞2 时，掺混损失较小，综合可知总压恢复系数与流量系数降低，且降低幅度小于宽高比为2 的情况。随着出口宽高比增加，局部加速损失减小，壁面摩擦损失增大，这些流动损失的影响趋势相反，影响效果近似，最终导致总压恢复系数与流量系数变化幅度相近。推力系数的变化与总压恢复系数和推力矢量角均有关联，随着出口宽高比的增加，喷管的推力矢量角先减小后增大，综合考虑总压恢复系数与推力矢量角带来的影响，当出口宽高比＜3 时，推力系数变化率相近；当出口宽高比＞3 时，推力系数的变化率逐渐增大。

4 结 论

以涡扇发动机双S 弯喷管为研究对象，基于串行双向松耦合方法研究了不同出口宽高比对双S 弯喷管的双向流固耦合特性影响，主要结论如下。

1） S 弯喷管的结构变形特征主要位于S 弯第一弯下游通道及喷管等值段出口上壁面，随着出口宽高比增加，由于第一弯通道形状、出口等值段形状逐渐“扁平”化以及S 弯喷管弯曲程度逐渐增大的影响，喷管第一弯下游上、下壁面区域变形量逐渐增大，而出口上壁面的变形量先增大后减小，S 弯喷管上、下壁面的最大变形均出现在S弯第一弯下游壁面。由于喷管出口壁面向外膨胀，出口宽高比在耦合作用下相比设计值减小。

2） 流固耦合作用对喷管气动性能产生较大影响，总压恢复系数、流量系数及推力系数均大幅降低。当宽高比为2 时，由于流动分离造成较大流动损失，此时总压恢复系数降低了0.56%，流量系数降低了2.67%，推力系数降低了0.72%。当宽高比＞2 时，随着出口宽高比增加，流固耦合作用所造成的气动性能变化逐渐增大，在出口宽高比为10 时达到最大，此时总压恢复系数降低了0.36%，流量系数降低了4.34%，推力系数降低了1.37%。

3） 当宽高比为2 和10 时流固耦合作用对S弯喷管局部变形与气动性能的影响较大。在小宽高比情况时，由于流动分离产生较大掺混损失，导致气动性能的下降；当宽高比在2～3 时喷管沿轴向向上弯曲角度减小，推力矢量角减小。在大宽高比情况时，由于喷管构型导致局部变形过大，产生较大掺混损失与局部加速损失，导致气动性能的下降；喷管沿轴向弯曲角度随着出口宽高比增加逐渐增大，推力矢量角逐渐增大。