基于改进粒子滤波的无人机编队协同导航算法

岳敬轩，王红茹，朱东琴，ALEKSANDR Chupalov

哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001

随着无人机相关技术的不断成熟与相关产业的不断发展，无人机凭借着其体积小、成本低、机动灵活和视角宽广等特点，在快递投送、空中摄影和节目表演等民用领域以及军事侦察与探测领域得到了广泛的应用与关注［1］。与此同时，随着军事民用领域所执行任务日趋多样化、复杂化以及作战模式趋于多元化，单个无人机执行能力有限且无法满足需求，这也就促进了无人机编队相关技术的诞生［2］。而精确的导航和定位信息是编队技术的关键，是实现无人机群航迹规划、稳定飞行和任务顺利执行的重要保障［3-4］。

目前，卫星导航是无人机群定位的主要方法，但仅依靠卫星导航，无法应对无人机群在城市和丛林等区域执行任务时，由于遮挡所导致的卫星导航无法使用的情况［5］。因此，通过无人机之间的信息交互来完成协同导航，从而提升无人机群的定位精度的方法已成为当下的研究热点［6-7］。

扩展卡尔曼滤波（Extended Kalman Filter，EKF）和无迹卡尔曼滤波（Unscented Kalman Filter， UKF）是非线性协同导航系统中最常见的融合算法［7］。EKF 需对非线性方程进行泰勒展开，通常只保留到一阶项，忽略其高阶项，将其近似为线性系统再进行卡尔曼估计，在线性化时可能会引入误差，从而导致系统发散。UKF 结合了无迹变换（Unscented Transform，UT）和卡尔曼滤波（Kalman Filter， KF），通过选取采样点，利用这些采样点的均值和协方差逼近非线性系统，避免了求解雅可比矩阵，对于强非线性问题有较好效果，但是其参数选择问题没有得到完全解决，且滤波效果易受初值影响［7-8］。此外，这2 种算法都是在高斯假设的前提下得到的最优估计，在算法仿真过程中采用的是理想化的高斯噪声，而在实际复杂环境下受各种因素的影响，多无人机（Unmanned Aerial Vehicle，UAV）协同系统的量测噪声常常会出现野值，这会导致量测噪声的概率密度不再服从高斯分布。

粒子滤波（Particle Filter， PF）理论上适用于任何状态空间模型，不受高斯线性条件的约束，其思想是基于蒙特卡罗方法，通过从后验概率中抽取的随机状态粒子来表达其概率分布［8］，其主要包括序贯重要性采样（Sequential Importance Sampling， SIS）和重采样2 个阶段［9］。研究表明，重要性采样的权重方差会随着时间的推移而增加，导致粒子退化现象，即多数粒子权重几乎为零［10］。在实时系统中，为了在粒子数较少的情况下获得较高的估计精度，处理该退化问题的另一个重要方法是选择合适的重要性概率密度函数（Probability Density Function， PDF）［11］。文献［12-13］提出了扩展粒子滤波器（Extended Particle Filter， EPF）和无迹粒子滤波器（Unscented Particle Filter， UPF），并利用EKF 和UKF 给出粒子建议分布函数。EPF 可以获得较好的重要性密度，但是线性化处理带来了误差；UPF 虽然导航精度较高，但是计算效率太低且稳定性差，并且状态估计误差协方差接近过程噪声协方差［14］。文献［15］提出Huber 鲁棒容积裂变粒子滤波，在容积卡尔曼基础上基于Huber 函数融合L2 与L1 估计，得到粒子建议分布函数，容积粒子滤波可以计算重要性PDF 的二阶矩和高阶矩，但本身稳定性易受到容积点影响，且提出的算法也只是在高斯模型下进行了验证，有一定的局限性。在重采样阶段，常用的重采样方法是直接丢弃小权重粒子并复制大权重粒子，这样容易导致粒子多样性缺失［16］。人工智能算法为解决粒子匮乏问题提供了一条有效的研究思路［17］。文献［18-20］提出了基于遗传算法改进的PF，基本原理是重采样过程中对粒子进行交叉变异操作从而改变粒子权重，但是遗传算法等智能算法自身存在过早收敛问题，且计算成本也很大，导致滤波效果不理想。文献［21］提出了UKF 和自适应差分进化算法联合优化的PF 算法，在传统差分算法基础上采用自适应策略，避免出现过早收敛造成局部最优的现象，然而，该方法通过大量迭代来寻求最优解且依赖初值选取，在对实时性要求较高的高维协同导航系统中并不适用。

在现有研究基础上，针对单主多从式无人机搭载低精度传感器的情况，提出了一种改进的PF算法实现协同导航的数据融合，解决了复杂环境中强非线性模型下量测噪声时变且不满足高斯特性的问题，在保证实时性的情况下得到了更高的定位精度。首先利用Levenberg-Marquardt（LM）迭代优化的EPF 来近似估计状态量的后验PDF，与传统PF 使用先验概率作为重要性PDF不同的是，该方法需要在重要性采样阶段结合最新观测数据得到粒子的重要性PDF，从而优化采样粒子的位置分布。随后引入自适应权重因子提出快速重采样方法，可以实时调整重采样粒子数目，不同于传统PF 直接丢弃小权重粒子，快速重采样方法根据粒子权重将粒子分类，只对低于阈值的其他粒子进行交叉操作来提升小权重粒子的权重，从而保留了粒子多样性且降低了重采样计算复杂度。

1 模型构建

1.1 单主多从无人机编队运动模型

在无人机协同导航领域，一般以二维空间建立导航模型，即将无人机飞行轨迹投影到同一高度下的二维平面以简化问题。这样的模型构建虽然可以减少计算量，但同时无法知悉无人机群高度上的变化，与实际情况会有较大误差。因此，为了使研究更具有普适性，根据匀加速曲线运动学式（1）建立式（2）所示的系统状态方程。

式中：s0和v0分别为初始位置和速度；s和v分别为当前位置和速度；a为加速度；t为运动时间。

式中：Xk=[x，y，z，vx，vy，vz，ax，ay，az]T为其中一架从机k时刻的三维位置、速度和加速度状态量；Wk为模型k时刻的系统过程噪声且满足均值为0、协方差为Qk的高斯分布；G为过程噪声驱动阵；T为采样时间；F为状态转移矩阵，即

该模型本质上利用的是航位推算原理［22］，由于过程噪声的存在以及系统递推模型的性质，采用此方法构建的模型来估计无人机的位置时，每一采样时刻的速度和加速度噪声都会叠加到下一时刻的状态量上，从而导致误差随时间累积，以及导航精度的降低。因此，构建合适的观测模型，引入观测数据来校正状态量成为了重点问题。

1.2 单主多从无人机编队观测模型

考虑到单主多从式无人机群都搭载高精度的导航设备成本太高，规定主机搭载高精度导航设备，所有从机搭载用于自身定位的低精度传感器。从机可以利用主机的高精度导航设备获取的准确位置信息通过解算来校正从机的状态量，实现协同信息的融合，抑制误差累积。观测模型为［2，23］

式中：p和v分别为GPS 获得的从机绝对位置和速度信息；S、α和β分别为主从无人机之间的相对距离、相对航向角和相对俯仰角的观测量。

相对导航信息的具体量测函数为［2］

式中：xm、ym和zm为主机位置信息；x、y和z为从机位置信息；R'k为相对观测噪声。

2 改进粒子滤波协同导航算法

2.1 LM 优化的迭代扩展粒子滤波算法

传统的PF 算法并没有考虑最新的量测信息，在观测模型精度较高的情况下容易导致较大误差，同时采样粒子的位置分布准确度很大程度上决定了算法的性能优劣，选取合适的重要性PDF 将会改善这类问题。

EPF 是在采样阶段用EKF 计算每个粒子的一阶矩、二阶矩，计算的同时引入最新的量测量来近似后验PDF［23］。产生合理的建议PDF 的过程中，利用LM 方法在状态更新时多次迭代，同时调整协方差矩阵，使粒子的分布更接近于目标的后验分布。

式中：pN(Xk|Z1：k)为满足高斯特性的PDF；N(·)为高斯分布和为状态量均值和协方差。基本步骤和原理如下所示。

步骤1初始化

k=0 时，设定初始状态量X0，从先验PDFp(X0)中采样N个初始粒子～p(X0)，初始粒子权重为=1/N，初始协方差矩阵P0为

步骤2重要性采样

1） 采用局部线性化的方式得到状态转移矩阵F、过程噪声驱动阵G、量测矩阵H、量测噪声驱动阵R，利用EKF 算法得到状态预测值和先验协方差。

式中：为k-1 时刻第i个粒子的估计值。

2） 采用LM 迭代优化的EKF 算法对式（10）和式（11）得到的均值和协方差进行迭代处理。大多数的算法更新迭代过程是利用Gauss-Newton 方法求解，然而由于线性化等误差的引入以及状态空间模型与观测数据存在差异，导致状态的观测更新不能保障估计误差的一致减少，使得协方差阵的估计值要比真实值偏低，因此Gauss-Newton 迭代方法收敛速度较慢，性能不太稳定。基于LM 的迭代方法将量测更新过程转换为最小二乘问题，在每次迭代过程中使用参数μi调整状态量的协方差阵来进行更新，当μi较大时，LM 迭代更接近Gauss-Newton 迭代。μi一般由模型的雅可比矩阵求得，具体取值参考文献［25］，该文献已从数学推理角度证明其收敛性。在不同环境下分配给μi不同的参数值，可以获得最优的状态估计和方差估计。

基于LM 优化修正后的协方差矩阵为

设进行M次迭代，对于j(1 ≤i≤M)次迭代，有如下计算步骤：

式中：为第i个粒子在第1 次迭代的初始后验信息；为k时刻的先验信息。

观测矩阵雅可比矩阵为

滤波增益矩阵为

第j+1 次迭代的协方差矩阵为

更新后的状态量估计值为

迭代终止条件为

式中：ε为预先设定的最小误差阈值。

假设c次迭代后迭代终止，则k时刻的状态估计和协方差为

3） 通过重要性采样得到重要性PDF，即

步骤3计算粒子权重

按式（23）和式（24）更新粒子的相应权重并进行归一化处理，分子中的第1 项和第2 项分别是似然函数和状态转移概率［9］。

2.2 快速重采样模型

重采样主要是为了进一步解决SIS 中存在的粒子退化现象，即经过几步迭代之后，出现大部分粒子的权重变得很小而少部分粒子占据较大权重的现象。图1 为重采样示意图，圆点表示粒子，圆点的面积大小代表了粒子权重大小。为了防止大量的计算浪费在大部分的小权重粒子身上，传统的PF 算法直接舍弃这些粒子，从而导致了粒子匮乏，降低了粒子多样性。

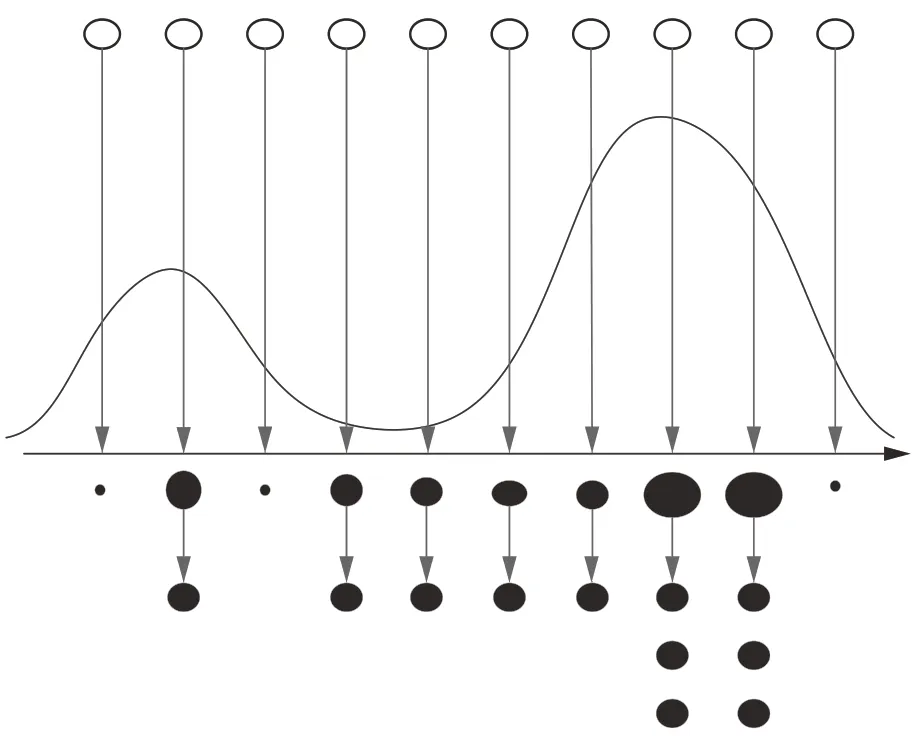
图1 重采样示意图Fig.1 Resampling diagram

由于对所有粒子都进行重采样操作会增加计算量，导致实时性较差。为解决此问题，本文提出了快速重采样（Fast Resampling， FR）方法，在保留粒子多样性的同时降低了算法复杂度。FR 方法首先在重采样时刻对粒子进行预处理，让小权重粒子向高似然区域移动，提高其权重。然后根据设定的粒子权重阈值对粒子进行分类，得到2 类粒子即中等权重粒子以及其他粒子。中等权重粒子不对其进行重采样，对另一集合包含了大、小权重的粒子进行抽样尺度判断，判断是否进行重采样。具体步骤如下所示。

步骤1预处理

k时刻的加权粒子集合对可以表示为如果则产生新粒子重新计算其权重，并保证新的权重介于和之间。

步骤2粒子集分类

其中，A 类粒子为大、小权重粒子的混合集合，B 类粒子为中等权重的粒子集合。B 类粒子权重大小中等，粒子稳定性高，直接保留。

步骤3A 类粒子重采样

求出A 类粒子的有效抽样尺度为

设定抽样尺度阈值为Nth=2×NA/3，当Neff＞Nth时，粒子集有效性高，不进行重采样。否则，选取2 个粒子使用式（26）所示的欧式距离表示其分布关系，欧氏距离可以简单有效地反映粒子位置拓扑关系。

式中：γ为粒子维度。

优化处理后新的粒子权重为

式中：Ta=1+log2dmn，Ta为自适应权重因子，一般为整数。当dmn接近0 时，2 个粒子位置接近，2个粒子不需处理。

经过自适应重采样处理后的小权重粒子达到B 类集合的选取范围则保留下来，否则丢弃，由大权重粒子复制补齐粒子集。

为了进一步证明所提出的FR 方法计算效率高，参考文献［26］对其他几种经典重采样算法的复杂度进行比较，表1［26］记录了不同重采样算法的运算操作数。其中M为残差重采样的残留粒子数。对比表1，本文提出的FR 方法采用分类处理的手段，参与重采样的粒子数最大为NA，大幅降低了计算复杂度，提高了协同导航实时性。

表1 不同重采样算法的运算操作数比较［26］Table 1 Comparison of operational operands of different resampling algorithms［26］

图2 描述了采用PF 和快速重采样PF（FastResampling Particle Filter， FRPF）在状态估计中的粒子权重大小对比。可见，PF 进行状态估计时小权重粒子占比越来越多，大权重粒子占比较少，容易导致多数粒子被淘汰；FRPF 将小权重粒子经过优化处理后，权重会增大。这会避免经过多次迭代后，大部分粒子都是由少数权重较高粒子复制而来的情况，大幅降低粒子贫化现象，在进行状态估计时几乎不存在粒子权重差异较大的现象。因此，本文所提出的方法能够有效地保留粒子多样性。

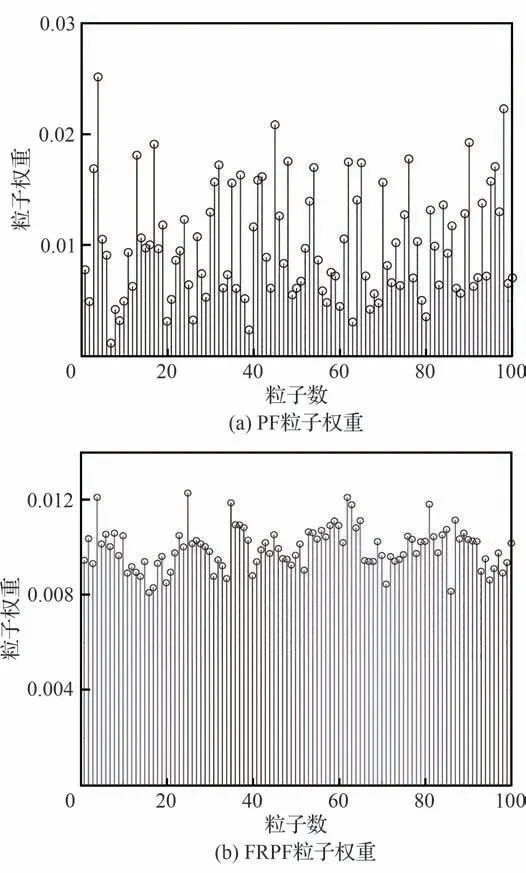
图2 粒子权重对比Fig.2 Comparison of particle weights

步骤4重采样并输出系统状态估计

由式（24）先对权重归一化，最终得出N个粒子的加权值，即改进PF 的滤波结果：

综上所述，改进PF 的无人机编队协同导航算法步骤如算法1 所示。

?

3 协同导航实验结果与分析

为了验证算法的可实施性和导航效果的精确性，本文进行了实验数据的离线仿真，所设置的传感器参数参考自开源导航网站（www.psins.org.cn）和文献［23］。表2 列出了编队中主从无人机所搭载的传感器设备的配置参数，机群的导航信息由搭载的传感器获得，所有无人机均可与主机之间通信。图3 为实验用到的传感器，传感器噪声服从N(0，σ)的高斯模型。

表2 传感器配置参数Table 2 Parameters of sensors configuration

图3 实验设备Fig.3 Experimental equipments

同时设置了以下场景仿真所提出的算法的有效性：主从式无人机协同导航网络中主机为位置已知的移动节点，从机为位置解算的其余移动节点。实验仿真时长为1 000 s，采样周期为1 s，在此期间，主机依据高精度RTK 和INS 设备进行绝对导航得到较为精确的导航信息。从机通过GPS 获取位置速度绝对导航信息，同时对主机测距，并测得相对航向角和相对俯仰角来进行协同导航。

主机位置、速度和加速度初始状态为[0 m，0 m，0 m，10 m/s，-10 m/s，2 m/s，0.01 m/s2，-0.02 m/s2， 0 m/s2]T。主机飞行轨迹如图4所示，其中，x、y和z轴分别指向北、东和天方向。

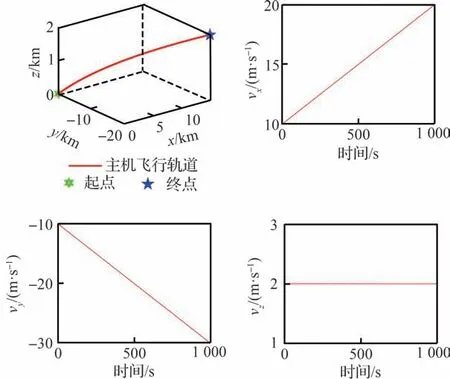
图4 主机飞行状态Fig.4 Master UAV flight state

从无人机位置、速度和加速度初始状态为[50 m，-40 m，0 m，10 m/s，-10 m/s，2 m/s，0.01 m/s2，-0.02 m/s2， 0 m/s2]T。状态方程在各方向上的位置误差ΔS=1 m，速度误差Δv=0.1 m/s。

非高斯噪声有闪烁噪声、异常观测值等类型，一般按式（29）处理方式简化表示为不同方差高斯噪声加权。

式中：σ1为传感器噪声；σ2为量测异常值；λ取值0.7；vk为k时刻加权噪声变量。

观测噪声中相对测距误差的测量时变野值Sk为

相对测角误差的测量时变野值θk为

考虑到无人机群是飞行速度较快的群体，因此导航的实时性非常重要。算法中采样粒子数不宜过大，N=100 为宜，LM 迭代次数为2。基于上述仿真条件，对单主从无人机编队进行仿真，分析其中一架从机的状态估计误差。用所提出的改进PF 算法与PF、EPF 和UPF 进行对比，其余算法均采用随机重采样，实验结果如图5～图7 所示。

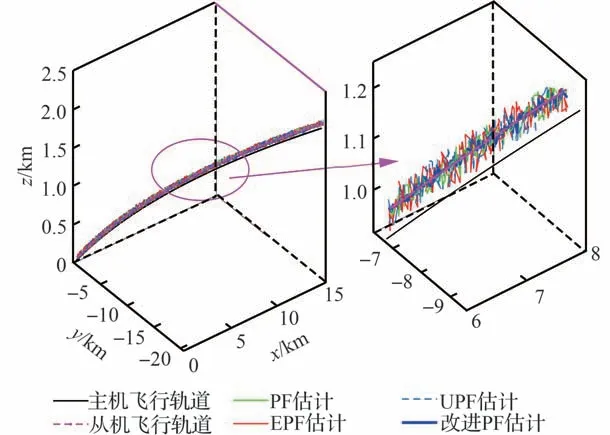
图5 仿真轨迹对比Fig.5 Comparison of simulation track

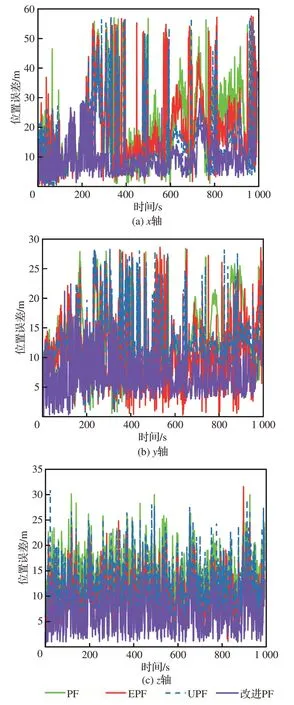
图6 各方向算法位置误差对比Fig.6 Comparison of position error of each algorithm in each direction

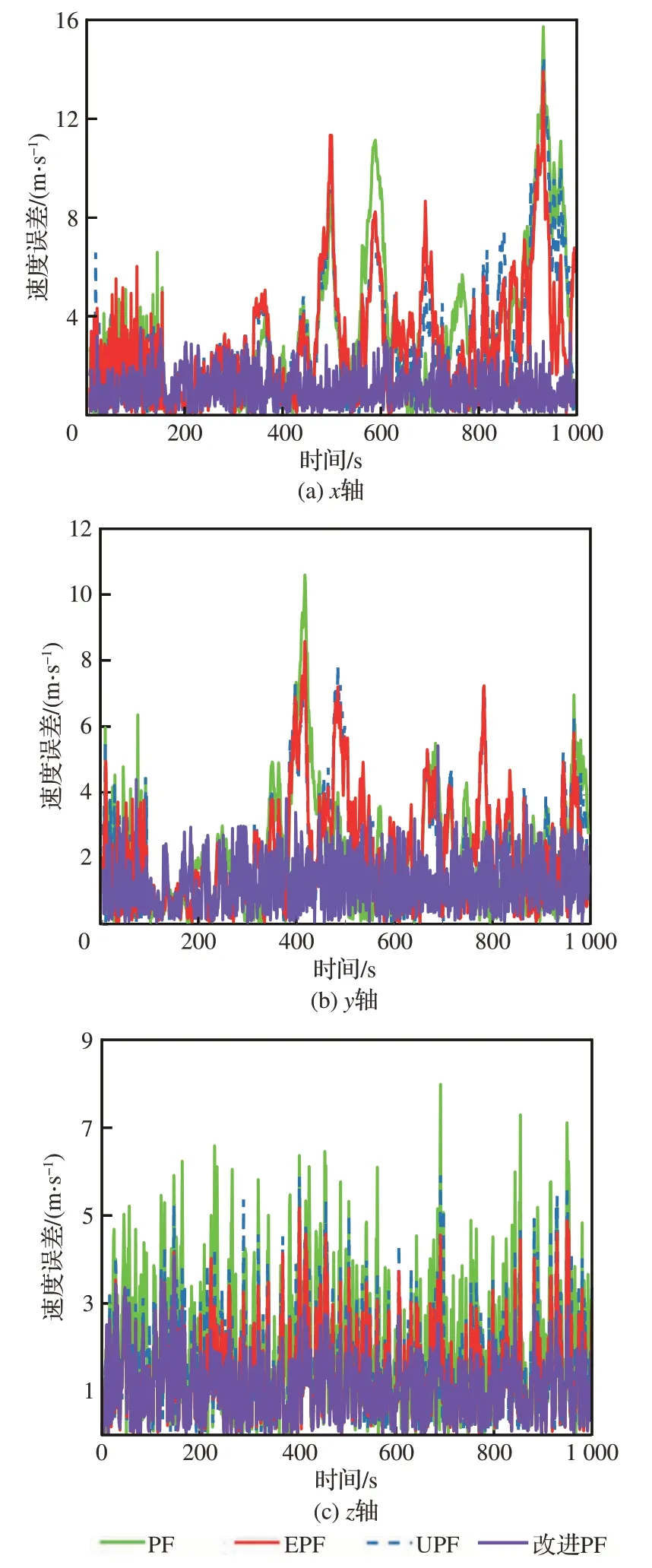
图7 各方向算法速度误差对比Fig.7 Comparison of velocity error of each algorithmin each direction

为了定量地分析4 种算法下的定位误差，进行了N次蒙特卡罗实验并统计了均方根误差（Root Mean Square Error， RMSE）来表示主从无人机协同导航的精度：

同时，仿真中记录了每一步迭代不同算法状态估计所消耗的时间来验证导航实时性，并求出平均值。表3 为1 000 s 仿真时间内4 种算法的三维位置误差均值和平均计算时间。其中位置误差均值计算公式为

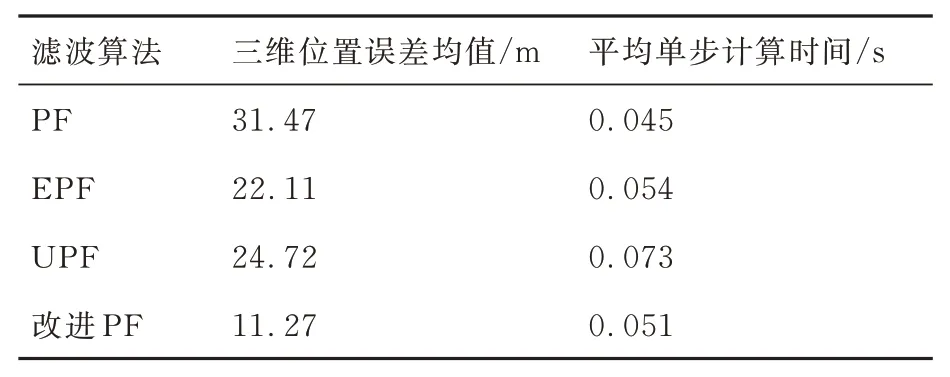
表3 各算法平均位置误差和单步计算时间Table 3 Average position error and single step calculation time of each algorithm

式中：Errx、Erry和Errz分别为x、y和z轴的误差。

通过图5～图7 和表3 可以清楚看出，PF 具有最快的计算速度，但随着时间的推移，会出现误差累积，并且三维坐标系中的位置和速度均方误差是最不稳定的。EPF 轨迹在初始阶段具有较好的滤波效果，但当噪声伴随异常值时，精度在x轴方向的下降更为明显，速度误差高达4 m/s，滤波后的轨迹也开始偏移飞行轨迹，计算速度较快，但导航效果并不理想。UPF 由于太过依赖Sigma 点的位置选取，导致其各方向上滤波效果差异较大，计算速度慢，导航效果一般。本文提出的基于LM 调整预测协方差的EPF 结合快速重采样方法的改进PF 实现的导航效果最好，计算速度与PF 相差不大。随着滤波收敛，各方向位置误差基本在8 m 以下，整个仿真时间的三维位置误差均值为11.87 m，各方向速度均方误差基本在1 m/s 左右，在前150 s 的高斯噪声下，各方向位置和速度误差稳定，误差较低；在后续的非高斯噪声下，误差波动较小，状态估计值不会随着时间的推移而发散，导航效果明显优于PF、EPF 和UPF。

为了进一步验证复杂环境下所提出的算法的鲁棒性，进行了GNSS 拒止条件下的实验。在上述仿真条件基础上，主从无人机GNSS 设备无法提供绝对导航信息。主机依靠高精度INS 设备短时间内依旧可以保持较高的导航精度，从机只利用相对导航信息来减小误差，表4 和图8 为实验结果。

表4 复杂环境下改进PF 算法的三维误差Table 4 Three-dimensional error of improved PF algorithm in complex environment

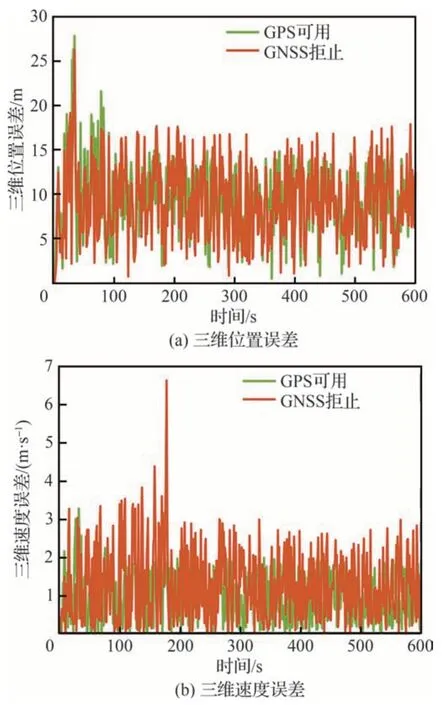
图8 复杂环境下改进PF 算法的鲁棒性Fig.8 Robustness of improved PF algorithm in complex environment

在GNSS 拒止环境下，本文所提出的算法在仅利用协同信息时仍能实现定位。虽然主机只使用INS 进行导航本身带来了误差累积，但从机位置误差与GPS 可用情况下的误差基本接近，失去低精度的GPS 绝对信息后虽然误差波动略大但收敛速度略快。此外，由于GPS 可以观测绝对速度，而导航传感器则无法观测到速度信息，因此本文所提出的算法虽然速度误差虽然较高，但也基本维持在1.5 m/s 以下。

4 结 论

本文提出了一种改进的PF 算法，用于搭载低精度传感器无人机群的协同导航。该方法由LM 优化的EPF 结合最新的量测量得到粒子的重要性PDF，从而使得粒子分布位置更为准确；同时提出快速重采样策略来改进传统PF 的重采样阶段，从而保留了粒子多样性且避免了粒子退化，大幅提高了算法的速度，保证了协同导航的实时性。仿真结果表明，与PF、EPF 和UPF 相比，本文提出的算法整体滤波效果较优，计算速度较快。改进的PF 算法仅通过粗略的测量便可准确地校正误差，这可以减少编队中高精度导航设备的数量，降低成本；同时所提出的算法在GNSS 拒止条件下鲁棒性较高，这也提高了复杂环境下协同导航性能。但单主结构太过依赖主机，未来可以在多主结构上深入研究，并进一步与协同导航算法相结合。