转化思想在初中数学解题中的应用研究

摘 要：文章示范转化思想的运用，让学生从多角度分析与求解问题，从而提高学生的解题能力.

关键词：初中数学；转化思想；解题

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2023）23-0005-03

收稿日期：2023-05-15

作者简介：韩为平（1982.10-），女，浙江省宁海人，本科，中学一级教师，从事初中数学教学研究.

利用转化思想解题，不仅有利于学生分析与解决问题，而且还能帮助学生更好地巩固与理解学习的基础知识，以增强新旧知识之间的衔接，增强学生的学习兴趣，提高学生的数学核心素养.

1 转化思想在初中数学解题中应用概述

转化思想就是在研究与解决问题时，通过某种方式对问题进行转化，以达到解决问题的目的.一般来说，是将复杂的问题转化成简单的问题，将难解的问题转化为容易的问题.总之，利用转化思想把陌生化为熟悉、复杂化为简单、抽象化为具体，从而使问题得到解决^［1］.教学中，学生已具备了一定的基础，在解决各种问题时，也可以判断出选择什么方法进行分析与解答.若教师仍通过固定思维约束学生，不仅会影响到学生的个性化需求，而且还会影响学生学习数学的积极性，从而影响学生的解题效率.而将转化思想用于初中数学解题，有利于学生积极主动地参与到问题的思考与解答中，让学生从多个角度来看待问题，掌握分析与解决问题的方法，使学生实现持续性发展.但是，依据教学存在的问题，教师可依据学生呈现的学习特点，对教学思想与教学策略进行调整，并对学生的思维发展情况进行引导，从而使学生学会转化问题、分析问题以及解决问题，并让学生完善知识体系，为以后的学习奠定扎实的基础^［2］.

2 转化思想在初中数学解题中的应用策略

2.1 直接转化

直接转化主要指与习题相结合，创设相应的情境，依据学习的知识，将需要解决的问题转化成对应的定理、公式或者基本图形.通过直接转化解答问题，需深度理解题意，特别是挖掘题干中的隐含条件，并与自身的解题经验相结合，经过转化及推理，找到解题思路，有效解决问题^［3］.

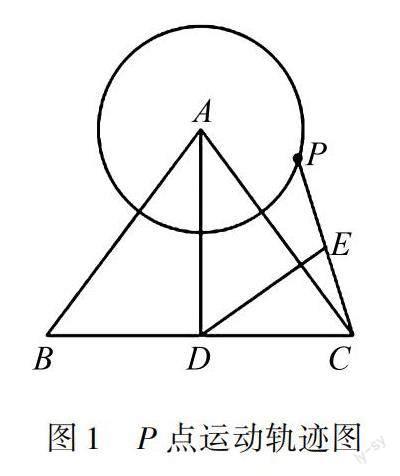
例1 如图1，△ABC中，AB=AC，BC=6，AD⊥BC于D点，AD=4，P是半径为2的圆A上的一个动点，连接PC，如果点E为线段PC的中点，连接DE，DE长的最大值是（）.

A.3B. 3.5 C.4 D.4.5

解析 通过直接法解答问题，可与已知条件相结合，联想有关的定义、图形性质等，构建相应的辅助线，通过更直接的形式呈现参数与线段的关系，以实现问题的高效解决.

综上所述，解题时运用转化思想，能将复杂、陌生的问题转化成简單、熟悉的问题，从而提高学生的解题能力.

参考文献：

［1］ 李斌.转化思想在初中数学解题中的应用与实践［J］.数理化解题研究，2022（29）：17-19.

［2］ 宋海明.转化思想在初中数学解题中的运用实践［J］.数理化解题研究，2022（17）：11-13.

［3］ 丁帮琴.转化思想在初中数学解题教学中的运用［J］.试题与研究，2021（30）：15-16.

［责任编辑：李 璟］