螺旋缠绕管式换热器传热性能优化与计算程序开发
2023-08-30郑蔚文刘红梅刘雪东张红红吕开新
郑蔚文,刘红梅,刘雪东,何 旭,张红红,吕开新,陈 荟
(1.常州大学 机械与轨道交通学院,江苏 常州 213164;2.江苏梅兰化工有限公司,江苏 泰州 225300;3.常州大学 绿色工艺装备重点实验室,江苏 常州 213164)
0 引言
换热器是化工行业中用于冷热流体热量交换的传统设备,是余热、废热回收利用的有效装置[1],在能源动力、医疗食品等行业有着十分广泛的应用,这就要求设备在满足生产过程中工艺需要的同时,能够尽可能实现提高能源利用率[2]。根据不同换热器传热机理的不同,工程中常用的换热设备主要有:蓄热式换热器[3-4],间壁式换热器[5-6]等。针对高效性能换热器的研究,一直是我国较多工业部门重点关注的问题。随着各行业对换热器产品需求的增加,如何实现新型设备的设计及其研究过程成为行业研究重点,符合当前发展需求的换热器仅依靠传统计算及设计的方式已难实现[7]。部分新型设备实验装备较大,且对设备性能产生影响的要素较多,若对所有因素均采用实验研究方法,会造成巨大工作量,甚至有的运行情况当前较难通过实验的方式实现[8-9]。
随着世界各国对如何实现对传统能源高效利用的更为重视,针对化工行业中新型结构设备螺旋缠绕管式换热器的研究也逐渐深入。与传统换热器的管程结构相比,螺旋管具有单位体积内大传热面积、结构紧凑的管排布方式、对管程热应力有一定克服能力等优势[10-11]。缠绕管式换热器的使用对实现工艺流程简化,换热设备数量减少等要求有极大帮助,更好地实现设备安全、高效能的运行环境[12],具有很强的市场竞争力[13-14]。与其他换热器相比,由于绕管式换热器可承受最大操作压力能达到20MPa,因此将其使用在高压低温条件工况中。目前,设备已运用在多个领域,特别是在大型天然气液化工艺中,设备使用率已超过90%,其造价占系统总造价约10%[15-17]。
加强对于缠绕管式换热器的研究对国内换热器进展具有推动作用。同时,在现代计算机技术高速发展的背景下,湍流计算模型的算法不断修改和完善,使用计算机技术对传统化工设备进行数值模拟,并对结果进行分析研究成为广泛使用的方法之一。其中,通过数值计算的方法对传热学与流体力学中的问题开展求解和研究,是研究流动与传热问题的理想而有效的方法。最终将计算机软件开发技术与化工设备相结合,实现计算过程简练化及计算结果可视化。
李书磊等[18]设计了一个简单的数值模拟模型进行对于管侧流动与换热的数值模拟,并运用已有文献中的实验数据与模拟结果进行对比,验证计算模型与数值模拟方法的准确性。研究在不同结构参数下换热器管侧甲烷流动的变化。通过正交试验的方式,得到了一组传热较好的管程参数组合,为换热器后续的优化研究提供数据参考。
李淑恒等[19]采用Fluent计算软件模拟了大螺距螺旋管结构在流体保持湍流状态下管内压降变化和传热特性,用以改善目前LNG绕管式换热器在设计时存在的管内低温传热不确定性。研究探讨了缠绕管结构、雷诺数等对管程总压降和努塞尔数的影响。分析模拟结果发现,管直径、管缠绕直径及雷诺数对压降和努塞尔数的影响均较为明显;管程螺距影响较小,可忽略不计。通过模拟数据,最终拟合出适用于LNG在低温冷却运行工况下的Nu公式,并将模拟值与Jayakumar等[20]实验得到的半经验值进行对比,验证模拟的可靠性。
Pan等[21]利用数值模拟方法,对缠绕管内振荡流的压降与传热特性进行详细研究,得到了管内流体振荡频率,流体入口速度与管程平均努塞尔数Nu,平均阻力系数f的关系理论,并利用场协同理论进行结论验证。
国内外诸多学者根据新型换热器工艺流程建立计算模型,并结合换热设备计算流程进行了计算程序开发,通过与手动计算数据对比分析误差,实现计算软件的工业化应用。采用的开发思路及方法对本课题有重要的参考意义。主要研究内容如下:
张周卫等[22]开发出一种针对双股流逆流型结构的绕管式换热器的工艺计算方法。将运用模拟结果确定的管程结构参数与管程流体为甲醇的工况编程写入程序,并实现对管束的相关计算,简化对于管束设计的工艺流程,获得总体设备结构相关参数,便于后期建模工作的开展。
梁琳等[23]提出了一套适用于相变流动工艺下绕管式换热器的计算模型,并将模型运用在具体传热流程计算中。结合模型已知参数与工况数据,完成绕管式换热器计算软件的开发,并通过将计算结果与传统的手动计算方法进行数据对比分析,得出软件计算误差,验证实际工业运用中计算软件的可行性。
薛佳幸[24]编程开发了一款能够实现单股流和双股流两种缠绕方式换热器计算的MCHE软件,其中两类换热器使用两种不同的设计计算方法,程序中包括对缠绕管的选择、管壳程流体物性参数选择、管道排列方式与配管计算、设备几何参数计算、换热器传热系数计算、管壳程压力损失校核等模块,并将所有的计算结果保存输出在Excel表格中,通过Visual C 语言调用Excel中的Worksheet,并访问Excel软件中的从属对象、属性等,以便程序使用人员对计算结果进行分析研究。
1 方法介绍
1.1 计算流体力学
20世纪70年代,最早的计算流体力学(CFD,computational fluid dynamics)软件诞生于美国,此后经过软件版本不断地更新和计算方法持续地改进,软件逐渐成熟。随着计算机技术的发展及计算机性能的提升,CFD更加得到多学科领域的重视与发展。作为一门融合了数值计算与数值可视化等技术的新兴学科,CFD在独立于实验测量,理论分析的前提下,能够高效解决换热计算,流体流动等多种问题。
CFD求解方法中依靠三大基本方程是:质量守恒方程,动量方程(N-S方程),能量方程[25],获得了各离散点上关于流动和传热的数据,进一步实现流对于流体流动和传热的模拟。
目前数值模拟技术中较为常用的方法是有限元法和差分法[26],其中Fluent软件是CFD 领域中应用较为广泛的一款基于有限体积法的流体计算软件。换热器作为传统化工设备,较早地开始使用数值计算软件进行相关模拟研究,相关文献较为广泛[27],因此本文采用Fluent软件对螺旋缠绕管式换热器进行数值模拟计算。
1.2 湍流模型与壁面函数
螺旋缠绕管式换热器几何结构复杂,管程流道曲率较大,其流动方式属于湍流流动。由于湍流流动的流动机理较为复杂,对计算设备性能要求较高,按照不同机理将湍流模型类别分为直接模拟(DNS)和非直接模拟。其中非直接模拟中包括:Reynolds平均法,大涡模拟,统计平均法。其中,在Realizable k-ε两方程模型针对湍流粘度的计算过程中,引入了针对流体曲率和旋转的内容,这对于螺旋缠绕管式换热器这种存在大曲率结构设备的流动计算更为有利。然而,由于固体壁面周边的流速通常较小,因此常处在低雷诺数或非充分发展湍流工况下,为提升结果精准度,在模拟中引入壁面函数概念,对模拟中使用的湍流方程进行一定修正。
在尺度化壁面函数概念中,认定壁面和粘性子层的边界重合且一致,在网格划分过程中使流体单元在粘性层之上,避免了由于边界层加密网格的存在而导致网格的不连续性,对后续模拟产生影响。综上分析,本研究中采用尺度化壁面函数实现对湍流方程的修正。
1.3 数值模拟研究思路
本研究中,采用Solidworks软件对螺旋缠绕管式换热器管、壳侧结构进行几何建模,并将几何模型导入到Workbench中进行进出口、固体域流体域等的划分和设置,利用Fluent Meshing实现网格划分,并用Solution模块进行求解计算。具体步骤如下:
1)结合目前行业现状,设计合理的计算模型结构,并用Solidworks建立相应的单层多圈数绕管模型和多层多圈数绕管模型。另存为x_t文件类型方便后期处理及计算。
2)在Fluent Meshing中导入模型文件。由于模型结构复杂,选用软件中的马赛克网格(Poly Hexcore)模块,设计合理划分程度,确定边界层厚度与层数,完成多边形网格划分。
3)确定微分方程和具体运行条件。
4)将包括.dat文件和.cas文件在内的计算结果文件导出。对模拟结果部分节点处数据进行导出,同时将文件在ANSYS CFD POST中打开,对设备的换热性能进行定性与定量分析,为之后的相关研究提供参考依据。
1.4 换热器性能评价标准
1.4.1 努塞尔数Nu
努赛尔数Nu是一个无量纲系数,表征为在流体对流换热过程中其导热热阻与换热热阻之比。其中,努塞尔数Nu的数值越大,表示流体的对流换热效果越好。努塞尔数Nu的计算公式如式(1)所示:
(1)
其中:h为流体对壁面的表面对流换热系数,W/(m2·K);λf为流体的导热系数,W/(m·K)。
1.4.2 阻力系数f
流体在设备内部流动过程中,采用阻力系数f来表征流动沿程受到的阻力大小。其中,阻力系数数值越大,表示流体在设备内流动过程中受到的阻力越大。阻力系数f的计算公式如式(2)所示:
(2)
其中:H表示壳程高度(m);Ds表示壳程水力直径(m);ΔP为流体流动过程中的阻力损失(Pa)。壳程水力直径Ds的计算公式如下所示:
(3)
其中:Vs为壳程体积(m3);Vt为管程体积(m3);Lt为换热管长度(m);Rt为换热管直径(m);H为设备高度(m)。
1.4.3 综合性能评价指数PEC
实现换热器传热性能优化的方式有很多种,不同的优化方法在改善传热性能的同时会增加一定的流动阻力等功耗。在多数情况下,流动阻力的增加大于强化传热。因此需要提出一个评价指标,能综合涵盖两种因素。PEC(performance evaluation criteria)是目前常用于衡量换热器综合传热性能的评价方法[28]。学者们结合阻力系数f及努赛尔数Nu概念,推导出PEC计算公式如式(4)所示:
(4)
其中:Nu0与f0表示同种工作介质下,相同参数工况下的努塞尔数和阻力参数,Nu与f表示优化后工况下的努塞尔数和阻力参数。当η大于1时,表明当前工况下的传热效果优于基准工况的传热效果,即当前工况下,传热效果得到强化;反之,当η小于1时,得到的结果相反。
1.5 数值模拟可靠性验证
1.5.1 误差计算
对选定的数值模拟方法进行结果可靠性分析是开展设备传热与流动数值模拟工作的前提。通过查阅文献,得到实验拟合出的表面对流换热系数计算公式,对公式计算值与数值模拟值进行误差分析,判断螺旋缠绕管式换热器数值模拟结果是否具有可靠性。实验拟合得到的表面对流换热系数h计算公式如式(5)所示[29]:
(5)
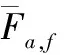
1.5.2 可靠性分析
结合实验公式,针对内外层管缠绕圈数均为10,壳程流速0.25 m/s,管程流速分别为0.5,1,1.5,2 m/s的运行工况进行表面对流换热系数h计算与对比,当误差β∈(-10%,10%),则认为该实验获得的数据具有可靠性。
通过表面对流换热系数h误差分析,由图可知,在4种工况下,平均误差为8.921 3%,误差β∈(-10%,10%)。根据可靠性定义,数值模拟结果具有可靠性,模拟方法选择可行。
图1 数值模拟误差分析图
1.6 程序开发语言介绍
作为一种特殊结构的优化型管壳式换热器,螺旋缠绕管式换热器在设计与计算过程中涉及了大量操作,计算过程十分复杂同时计算成本高。为提升计算效率,工业设计逐渐开始采用计算机程序完成计算工作。目前,已有一些运行稳定的可用于传统换热器的计算软件,如:HTRI、Aspen等,但针对新型换热器的计算软件较少,且均无缠绕管换热器计算软件[30]。
Visual Basic 6.0是Windows系统下的一款软件开发工具[31],具备基于Windows操作系统下的可视化编程环境。与其他开发语言相比,其具有许多优点。在本研究中,运用Visual Basic 6.0编程语言开发了螺旋缠绕管式换热器设计计算软件,通过程序计算为设备设计提供数据参考,并对设备流动传热性能等数据进行快速计算。
2 模型建立
2.1 数学模型
螺旋缠绕管式换热器中,壳程热流体的入口流速在0.25~1 m/s的范围内变化,由于管程螺旋结构对壳程流体有强烈的扰流作用,因此壳程、管程均保持湍流状态。基于实际工况对螺旋缠绕管式换热器计算模型做出如下假设:
1)管壳程中的冷、热流体在发生换热后,进出口温度温差均在10 K以内。因此,两种介质物性参数选定为对应温度范围内的平均值;
2)在数值模拟中,仅考虑设备各部分结构之间导热以及与冷热流体间对流换热情况;
3)管程壳程内的流动介质均为连续的不可压缩流体,且在筒体内壁,芯筒外壁及换热管处没有壁面滑移现象;
4)系统与外界保持绝热,无热量损耗。
针对上述假设和前期对数值模拟方法的选择,本章中螺旋缠绕管式换热器模型在直角坐标系中的控制方程如下:
质量守恒方程:
(6)
动量守恒方程:
(7)
(8)
(9)
能量守恒方程:
(10)
湍流动能方程k方程[32]:
(11)
扩散方程e方程[33]:
(12)
2.2 特征模型的确定
本课题采用ANSYS Fluent软件对双层多圈数缠绕的绕管式换热器进行详细模拟与分析。由于实际工业运用中,设备内部管数及管程缠绕圈数过多,传统数值模拟方法较难完整实现,计算成本较高且不能保证较好的准确性。因此,选择单层管数为2,管程缠绕层数为2,相邻层管程缠绕方向为同向交错的设备结构为课题研究的特征模型,模型结构如图2所示。对管、壳程介质的出口管道进行一定长度的延长来消除管、壳程流体的出口效应对模拟结果的影响。螺旋缠绕管式换热器中部分基本结构参数如表1所示。
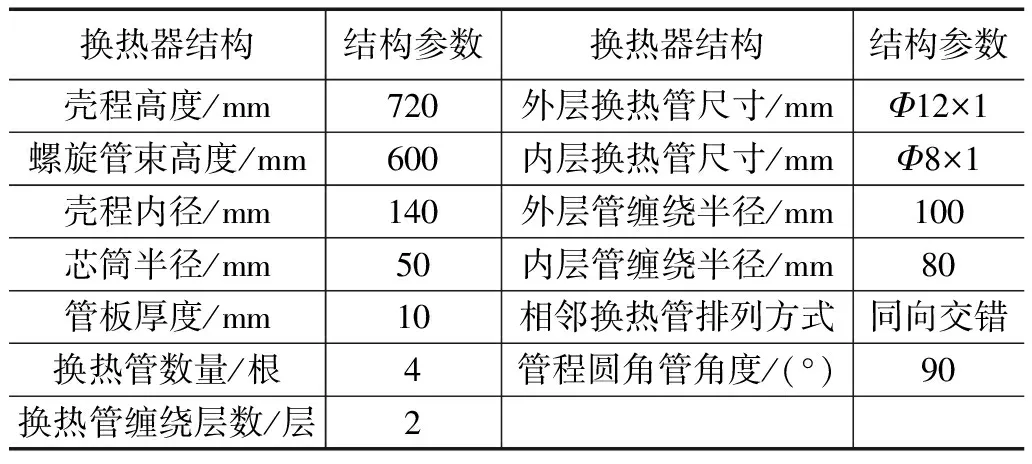
表1 螺旋缠绕管式换热器基本结构参数表
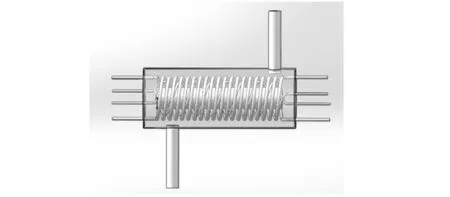
图2 螺旋缠绕管式换热器特征结构示意图
螺旋缠绕管式换热器特征模型中材料及相应的物性参数如表2所示。
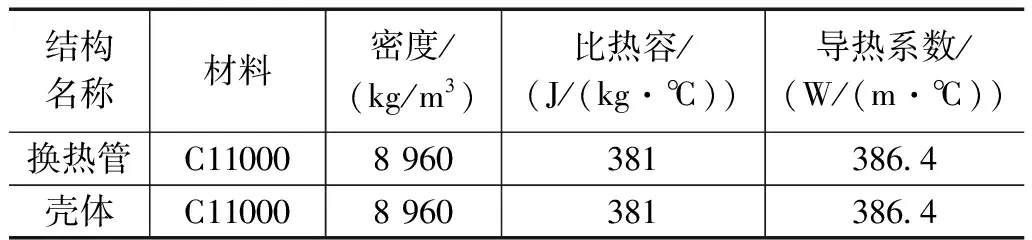
表2 设备材料物性参数表
螺旋缠绕管式换热器中管壳程介质的物性参数如表3所示。
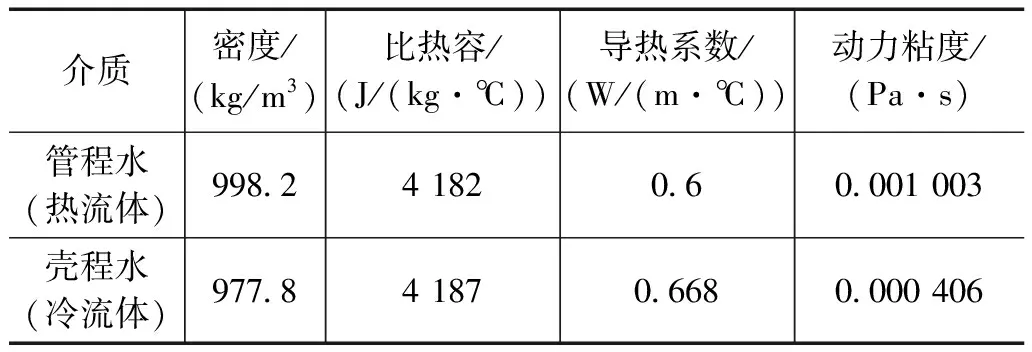
表3 管壳程介质物性参数表
2.3 网格划分
采用前处理软件ANSYS Workbench对螺旋缠绕管式换热器计算模型进行进出口设置与流、固体域划分。由于特征结构中管程结构螺旋缠绕十分复杂,为提高网格质量保证计算精度和准确性,采用Fluent-Meshing模块对计算模型划分多边形网格。
划分好网格后,为保证特征模型的网格无关性,在正式模拟前对模型进行网格无关性分析。对模型划分出网格数量F分别为10087236,11347872,12896231,14263278的4种不同网格。选择内外缠绕圈数为10,壳程流速0.5 m/s,管程流速1.5 m/s工况进行4种网格的数值模拟,并以壳程流体的出口温度T2作为监测对象。
对四组模拟中冷流体出口温度结果进行分析发现,当模型网格数量超过11347872时,出口温度基本稳定在290.1 K左右。综合考虑计算精度与时间成本,对计算模型均采用该网格设置进行模拟。当改变计算模型结构参数时,采用相同的验证方法确定模型对应的最优网格数量。
2.4 边界条件及求解方案
对螺旋缠绕管式换热器的计算模型分别定义管程和壳程两个流体域。因管程结构对流体扰流作用明显,经计算与文献参考,管壳程流体在设备流动过程中均处于湍流状态。
在设置边界条件时,壳程为热流体水介质,入口设置为速度入口(velocity-inlet),入口初始温度333 K,出口设置为压力出口(Pressure-outlet),出口压力0 Pa;管程介质为冷流体水介质,入口设置为速度入口,流体初始温度为283 K,湍流强度5%,介质出口为压力出口。换热管设置为壁面边界条件,并对其设置壁面导热,所有壁面均为无滑移边界。
模拟过程中,考虑到模拟收敛速度与计算精度,选用SIMPLEC算法对模拟进行速度与压力的耦合。管壳程换热介质均为不可压缩流体,动量方程以及能量方程均采用二阶迎风格式。将残差值作为检验计算结果是否收敛的依据。其中,除能量残差值收敛标准设置为10-5以外,其他变量均设置为10-4标准。当各变量的残差值均低于其对应的设置标准,且管壳程介质均遵循守恒定律时,认为该次计算收敛,计算停止。
3 数值计算模拟及性能优化
3.1 壳程流速对传热特性的影响
针对螺旋缠绕管式换热器用于数值模拟的计算模型,结合相关文献,当管程冷却水流速为1.5 m/s时,为探讨壳程热流体水介质的流速变化对螺旋缠绕管式换热器传热特性的影响,依次选取0.25 m/s,0.5 m/s,0.75 m/s,1 m/s这4个不同的壳程进口流速值,分别对其进行数值模拟,对比不同壳程流速下螺旋缠绕管式换热器的流动与传热特性。
螺旋缠绕管式换热器在不同壳程热流体水介质流速Lq下的传热系数K及其变化速率曲线如图3所示。结合实验所得表面对流换热系数h计算公式,对数值模拟进行验证。由图可知,螺旋缠绕管式换热器的传热系数公式计算值均低于其模拟值,但总体变化趋势保持一致。
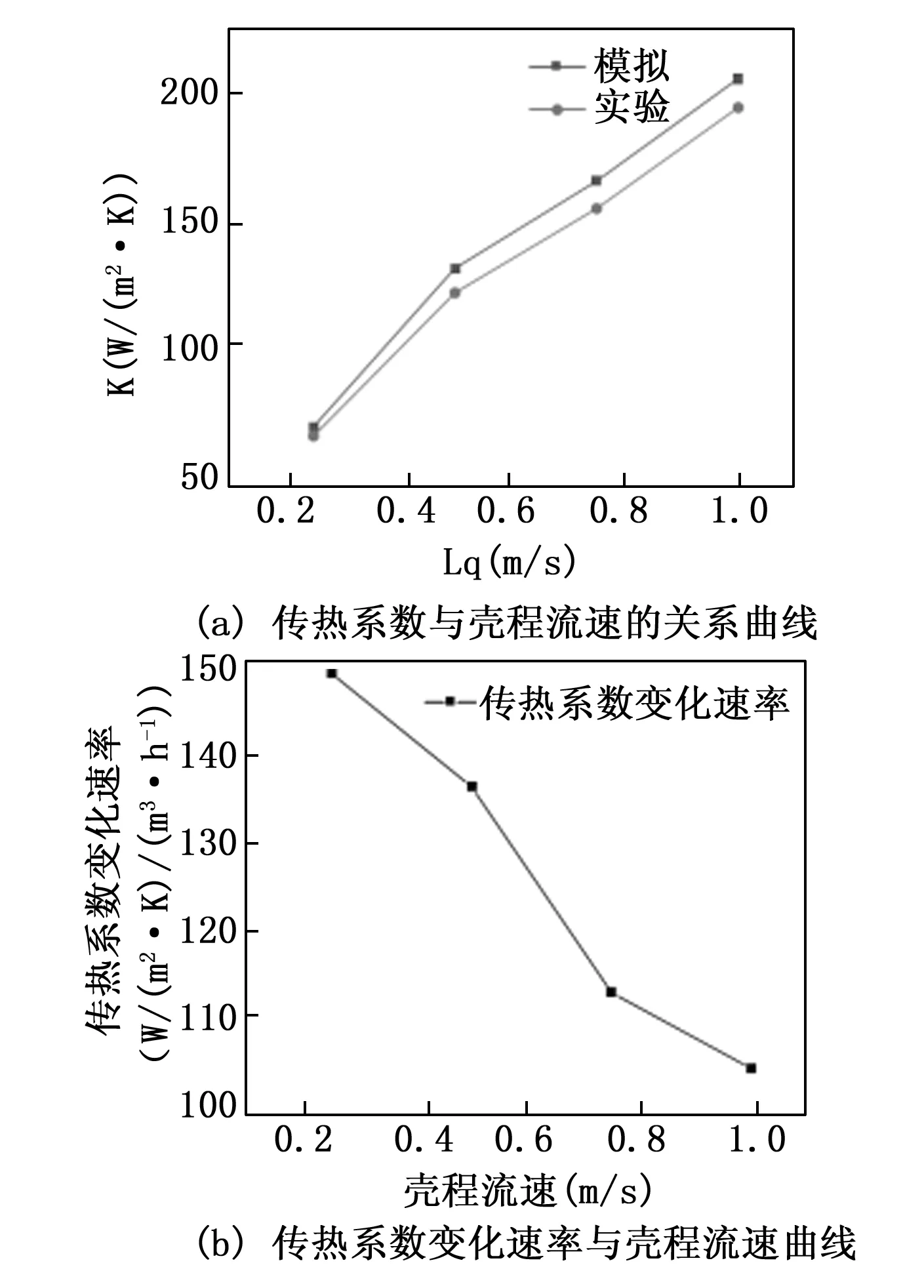
图3 数值模拟及公式计算值对比
流体的实际流动过程中存在一些不可避免的热损耗,数值模拟中流体流动为理想状态。尽管实验过程中对螺旋缠绕管式换热器设备及介质运输的相应管道等部件均采取了保温措施,流体的实际流动仍然存在不可避免的热损耗同时实验存在测量误差;另一方面,数值模拟过程中边界采用了壁面函数,其第一层网格点处于对数层中,这与实际情况有一定的误差,因此实验和模拟结果产生了一定的误差,平均误差为9.1%,在接受范围内。由此,验证了数值模拟的可靠性。
当壳程工作水介质流速超过0.75 m/s后,传热系数曲线斜率减小,同时,随着壳程工作水介质流速的增加,传热系数的变化速率始终保持正值,其中在0.5~0.75 m/s区间内变化速率最大,在流速大于0.75 m/s后变化速率放缓且明显降低。模拟结果表明,尽管螺旋缠绕管式换热器的传热系数随着壳程流速的增加而增大,但其增量不断减小。由此认为0.75 m/s是较为合适的壳程流速。
图4中,取XY平面上,Z=540 mm,Z=820 mm处流线进行观察分析。在壳程流动区域内,均存在较为对称的半月型螺旋式旋涡。由于管程多层缠绕的特点,对流体流动造成二次流作用,使壳程热流体在流动过程中受到来自管程结构的扰流。同时,由于螺旋管内的离心力,管程流体向管程外侧偏移并向两端挤压,基于流体连续性,形成一对流动方向相反的涡流,从而加强了管内外流体湍流程度,提升设备整体流动性能。
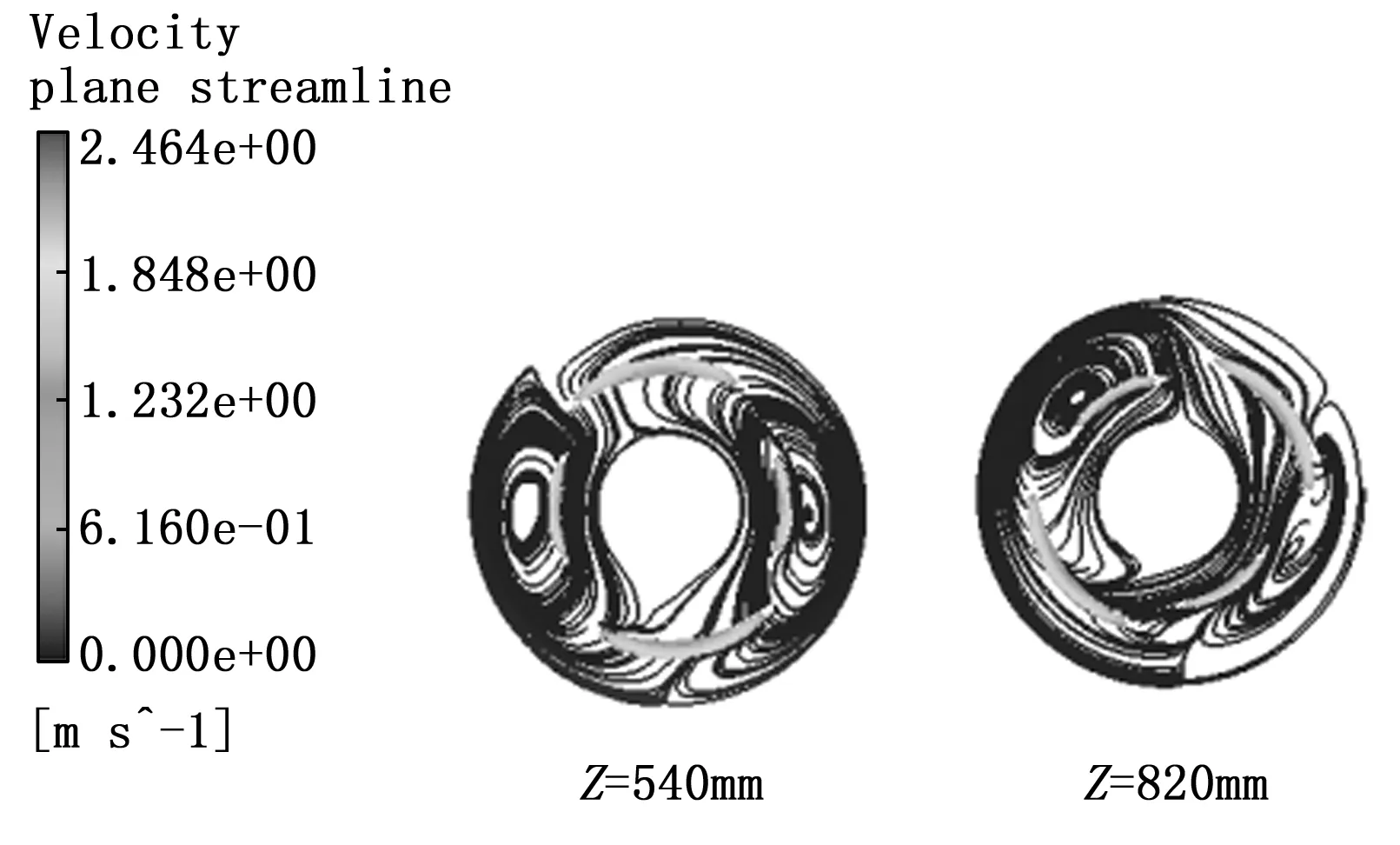
图4 特征模型壳程流线图
由图5观察可知,流体在流经缠绕管的弯曲段时,流体受到管内离心力作用,流体偏离流道主流方向向外侧流动,背离弯曲段受到了流体很大的挤压,导致背离侧速度梯度较大,管道内侧速度梯度较小。同时,由于管壁面存在一定的粗糙性和边界粘性,管内流体在中心区域受到的阻力较小,流体在中心偏上区域处速度较大。
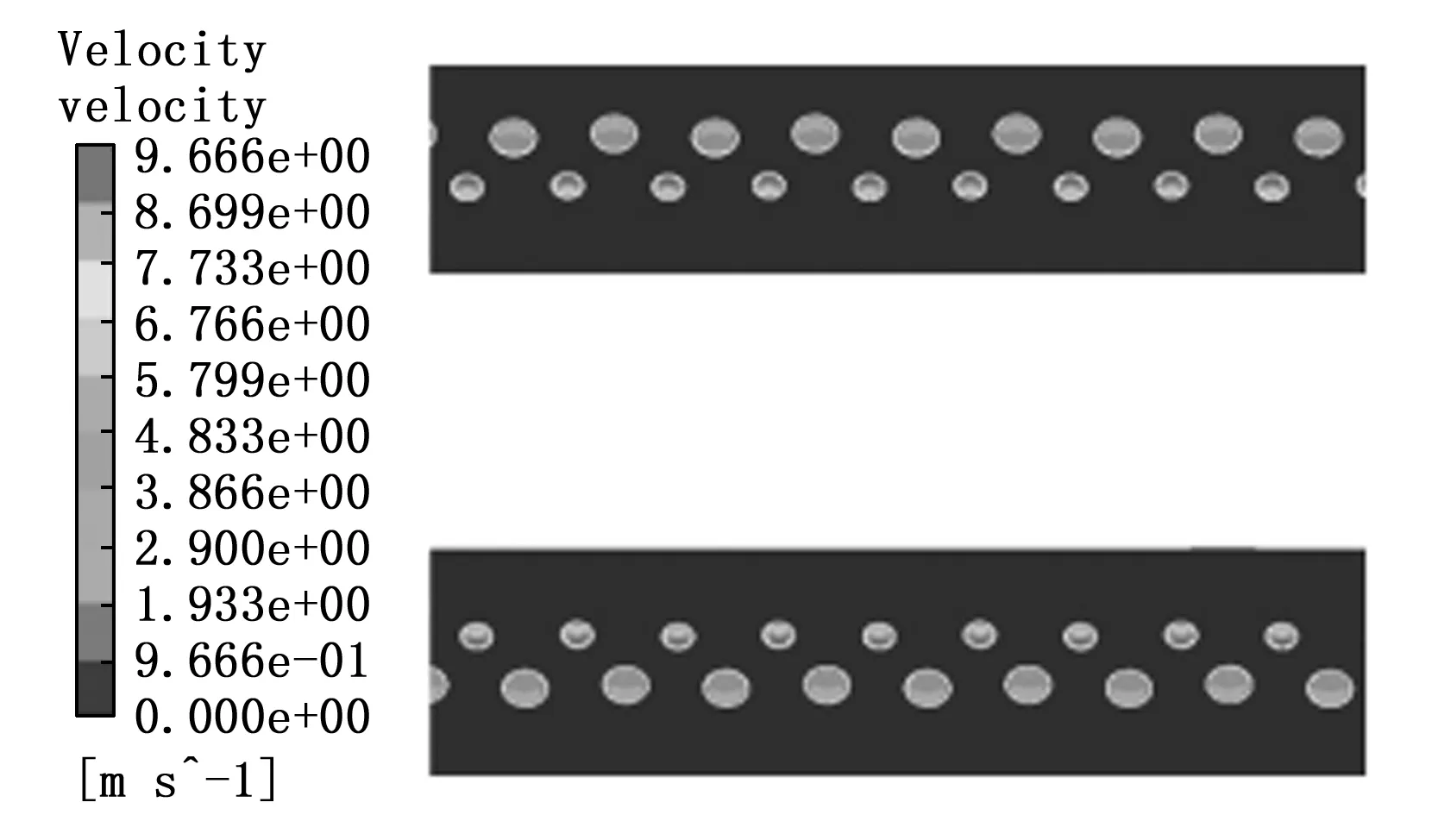
图5 特征模型壳程速度云图
3.2 管程排列方式对传热特性的影响
在2.1节中已经确定了换热器当管程冷却水流速为1.5 m/s时,最佳的壳程流速为0.75 m/s。在此流速下,分别对3种管排列方式:同向平行、同向交错、逆向交错的特征结构进行模型建立与数值模拟,从而探究不同管排列方式对螺旋缠绕管式换热器流动及传热性能的影响。
在同向平行缠绕方式中,内外两层管程缠绕方向相同,且内外层对应位置缠绕管起始缠绕角度相同;同向交错方式中,内外两层换热管缠绕方向相同,四根缠绕管起始角度分别为0,90,180,270;逆向交错方式中,内外两层换热管缠绕方向相反,四根缠绕管起始角度分别为0,90,180,270,实现内外层缠绕管交叉排列的结构。除相邻层管排列方式外,其他结构参数与2.1节中所列参数保持不变。
如图6所示,是不同相邻层间距下3种排列方式的努赛尔数Nu折线图,其中Type1为同向平行方式,Type2为逆向交错方式,Type3为同向交错方式。观察数据可知,同向交错排列方式下的Nu数高于其他两种情况,且逆向交错排列方式的Nu数最低。与同向平行方式下运行结果相比,由于缠绕管外壁面对壳程流体存在扰流作用,使得在同向交错方式下,相邻层管间隙之间出现更为明显的径向速度,从而促进管外壁面附近的壳程流体与管内流体充分换热。随着缠绕半径的增大,壳程流体在经过内外两层管之间的缝隙时阻力减小,层间流体流动换热效果提升,Nu增大。
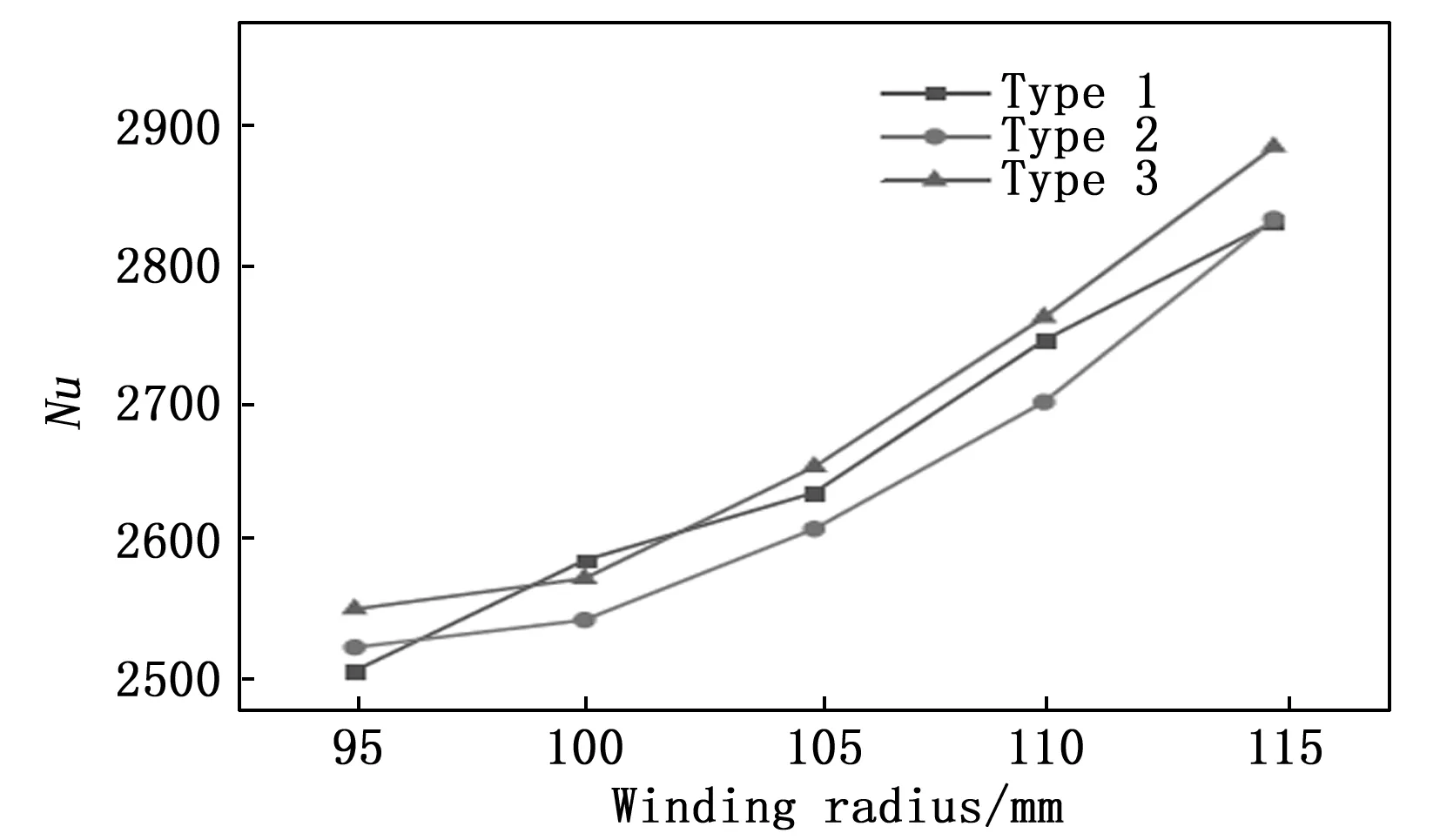
图6 不同相邻层间距下不同排列方式Nu折线图
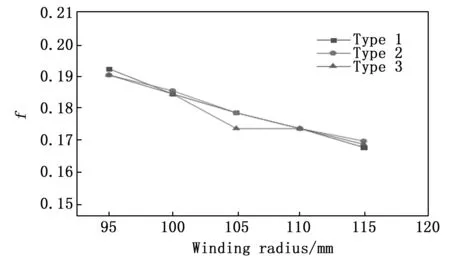
图7 不同排列方式下折线图
不同相邻层间距下3种排列方式的阻力系数f折线图如7所示。不同排列方式对阻力系数f没有较大影响,但总体趋势来看逆向交错排列方式下的阻力系数大于其他两种排列方式。这是由于逆向交错的方式使得壳程流体流动方向在经过螺旋管时变化更为明显,湍动程度更为剧烈,能量的损耗有小幅度增加,阻力系数变大。随着外层缠绕半径增大,内外两层距离增大,壳程在管程附近阻力减小,f减小。
3.3 管材料参数对传热特性的影响
本节针对螺旋缠绕管式换热器特征模型,控制其他参数不变,采用铜(C11000),铁白铜(BFe10-1-1),304不锈钢及316 L不锈钢作为换热管束材料,分别进行数值模拟,分析不同管程材料对设备传热特性的影响情况。4种材料的物性参数如表4所示。
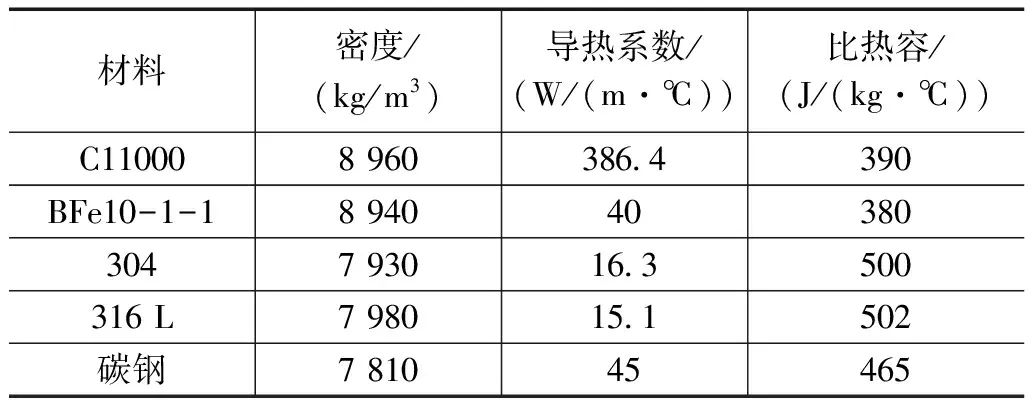
表4 管材料物性参数表
当螺旋缠绕管式换热器特征结构中管程同向交错排列,内层缠绕圈数为4,外层缠绕圈数为10,壳程流速0.25 m/s,管程介质流速1.5 m/s时,分别采用上述4种换热管材料进行数值模拟,其传热系数结果如图8所示。不同材料导热系数不同,由图可知,当换热管材料为C11000时,由于其材料导热系数为4种材料中最高,此时设备传热效果最好,且与采用316 L不锈钢的结构相比,传热系数高出了6.3%。
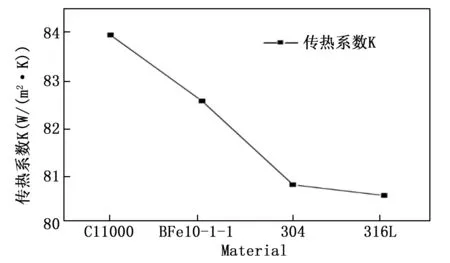
图8 传热系数结果
由于螺旋缠绕管式换热器是在管壳式换热器结构基础上进行的结构修改与优化,因此选择管壳式换热器相关关联式进行公式拟合。其中,管壳式结构换热器的传热系数K与管程材料导热系数λm的关系式如式(13)所示:
(13)
其中:当换热器其他结构参数及操作参数一定时,A,B均为常数,λm为换热管壁面材料的导热系数(W/(m2·℃))。
根据不同管束材料的模拟计算结果,在传统管壳式换热器传热系数K计算公式的基础上,利用Matlab软件对上述模拟结果进行线性拟合,拟合公式如式(14)所示:
(14)
为验证公式可靠性,修改管程材料参数为碳钢,其他参数保持不变,对公式进行验证。数值模拟结果中,壳程传热系数K为82.7,公式计算得到的换热系数K值为82.826,误差为0.15%左右,小于10%,证明材料参数传热系数拟合公式具有一定的准确性。
4 计算程序开发
4.1 开发流程
为保证程序能够正确解决实际问题,在设计前需要对用户需求,预期目标等进行清楚地认识。程序设计主要分三步进行,分别是:问题分析、算法设计、程序实现[67]。
1)问题分析:程序开发者对问题的已知条件进行分析,掌握解决问题的预期目标,明确程序需求。本计算程序期望对用户输入数据进行分析计算,将计算公式写入程序中,并在程序中实现结果输出,运用计算结果实现对设备结构的优化与改进。
2)算法设计:通过一种简单且可行性高的方式表达出当前需要解决的主要问题和解决方式,如:流程图等,对所需内容与输入数据进行整理。
3)程序实现:将算法用一种计算机语言来表达成程序,并采用多组数据对程序计算结果进行验证。本课题计算程序采用Visual Basic语言进行开发,能够通过简单的方式实现程序的可视化。
4.2 开发结果
通过对计算程序进行编写,将程序界面主要分为用户输入数据,计算结果输出两部分。操作用户通过在程序左侧输入部分模块对螺旋缠绕管式换热器的结构参数、操作参数、流体物性参数等进行已知数据的输入,程序会自动开始进行相关计算,并将相对应的计算结果输出至右侧输出部分。具体界面如图9所示,同时,部分代码内容截图如10所示,通过计算机语言对输入输出框进行编写,并对其结构样式进行说明和设定。
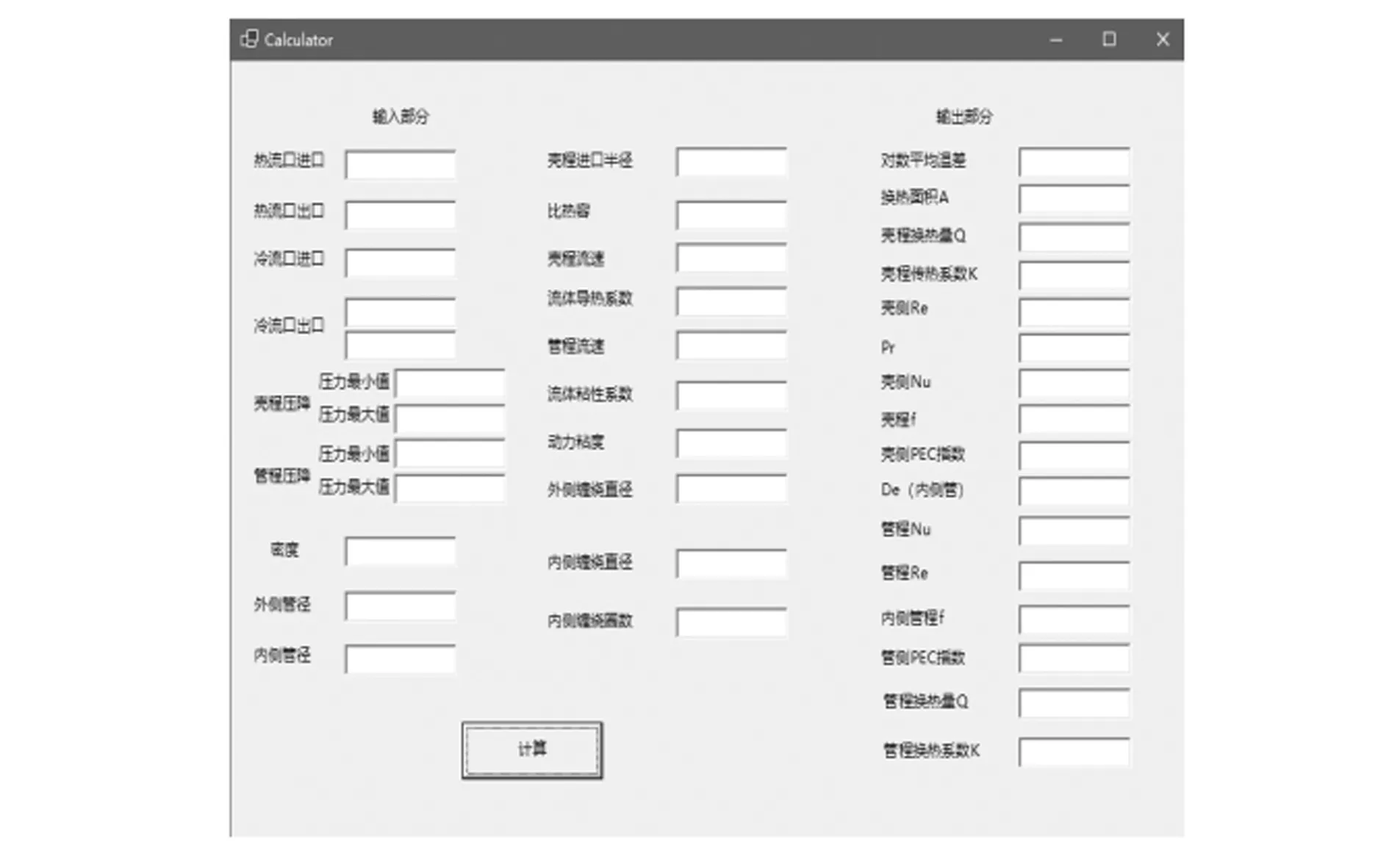
图9 计算程序界面

图10 部分代码截图
5 结束语
本文以螺旋缠绕管式换热器作为研究对象,通过修改多个结构参数实现传热性能提升,实现对能源的高效利用。主要研究结论如下:
1)通过改变壳程流体流速,对螺旋缠绕管式换热器进行多组数值模拟,并通过相关实验拟合得到的表面对流换热系数公式验证了模拟的可靠性。研究表明,当管程冷却水流速为1.5 m/s时,壳程热流体的最佳流速为0.5 m/s。随着壳程流体流速的增加,传热系数及壳程压降均增大。
2)当换热管呈同向交错排列时,由于其能够在增大壳程流体在管缝隙间湍动能的同时,不产生较大压降,通过交错的排列方式增强对壳程流体扰动,使冷热流体之间实现充分换热,此时,设备的综合传热性能优于其他形式排列的换热管。
3)通过改变4种常用换热管材料的计算模型进行模拟,得到传热系数与管材料导热系数的曲线图,并在传统管壳式换热器总传热系数计算公式的基础上,分析拟合得出螺旋缠绕管式换热器传热系数与换热管材料导热系数的关系式。
4)运用Visual Basic编程语言,结合数值模拟结果进行计算程序开发,实现对计算过程的简化,提升计算效率,并结合实验数据进行程序验证。
后续可以针对管内径、同一层管缠绕方向、相邻层管间距等参数进行传热性能影响分析,并得到参数相关的性能曲线,以对今后设备设计工作提供参考依据。
