问题驱动，渗透模型意识

徐永婷 戴志洪

［摘要］ 问题是数学的心脏，数学发展始终都在不断地提出问题和解决问题。恰当而有效的问题可以充分激发学生的求知欲，启发学生深层次思考。本文以“20以内退位减的复习”教学为例，立足学生的认知基础，巧用问题引领，让学生在有趣的游戏情境中经历完整的活动过程，理解退位减法的计算模型，培养数学模型意识。

［关键词］ 模型意识；问题设计；小学数学；游戏情境

一、巧设情境，提出问题

[情境一]回顾梳理20以内的退位减法计算方法

1.摘苹果游戏

谈话：在上课前，我们来和小猴比赛摘苹果吧！填一填表，谁愿意上来挑战？

提问：口算得又对又快，是有什么好技巧吗？

2.回顾算法

提问：就拿12-9来说，你是怎么算的？

预设：“破十法”；“平十法”；“想加算减法”。

学起于思，思源于疑。情境一中，教师设疑启智，创设了“与小猴比赛摘苹果”的问题情境，把学生带入“好玩好学”的游戏情境，引导学生发现问题。借助这样的情境，自然地引出20以内退位减的复习，让学生在摘的过程中回忆算法。学生遇到20以内退位减的算式，可以应用“破十法”“平十法”“想加算减法”的模型来计算。当然，这种计算方法也可以推广到其他数位的退位减法上，掌握计算模型，就能提高计算效率。

师生共同回顾算法后，学生展示和交流自己课前制作的思维导图，积累理解算理、形成算法的学习体验，体会到运用思维导图整理知识的简洁性，为今后的学习打下基础，也为模型的构建做好铺垫。

二、解决问题，构建模型

[情境二]观察20以内的退位减法表（表略）

提问：现在我们把这些摘下来的苹果放在这个表格里，可以怎么放呢？

追问：仔细观察，除了竖着看20以内的退位减法表，还可以怎么看？

预设：竖着看；横着看；斜着看。

1.问题引领

这张“20以内的退位减法表”藏了好多的数学奥秘，我们应该怎样进行探究呢？

预设：圈出任一横行或任一竖行，看看它们的被减数、减数、差是怎么变的；圈出左斜行或右斜行，看看算式的排列规律；任意读一行，就能找到规律。

2.自主探究

谈话：到底用哪种方法来探究规律比较合适？接下来我们进行一个小活动。

要求：（1）圈一圈：选择任一横行、竖行或斜行，将其圈出来；（2）看一看：仔细观察你圈的那一行的算式排列有什么规律。（3）说一说：和同桌交流你的发现。

3.序列交流

第一层次：粗浅观察到算式的整体特征（忽略了差的变化）。

预设1：竖着看，一列是十几减9，一列是十几减6，一列是十几减4。

预设2：横着看，一行是11减几，一行是13减几，一行16减几。

预设3：斜着看，一斜行的得数都是4，一斜行的得数都是7，一斜行的得数都是9，斜行得数是相等的。

第二层次：深度观察到算式的局部特征（关注了差的变化）。

预设1：竖着看，减数不变，被减数越大，差也越大。

预设2：横着看，被减数不变，减数越小，差反而大。

预设3：斜着看，被减数和减数同时多1或者少1，差不变。

明确：斜行的算式得数相等。

4.思维完善

谈话：通过观察对比和有序思考，我们进一步探究了20以内退位减法的规律，知道了看问题要全面。

建模，就是把抽象的理论转化成一种有“型”的模子，让学生在观察中发现、感悟、得出结论，既激发学生的学习兴趣，又培养学生爱观察、爱思考和爱表达的好习惯，以及解决问题的能力。孤立的算式往往看不出什么，教师巧用问题“如何把这些摘下的苹果放进表格里”来串联算式，让学生经历有效的活动过程解决问题，体会到数学与日常生活的密切联系，同時还得出了20以内退位减法表的结构化模型，积累学生的活动经验，培养推理能力，渗透模型意识。

三、完善结论，深化模型

[情境三]同题异构

谈话：你会运用这些规律解决一些实际问题吗？

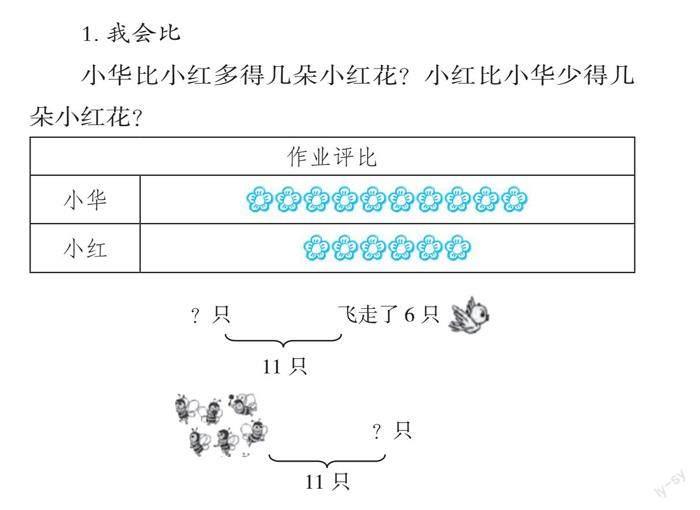
1.我会比

小华比小红多得几朵小红花？小红比小华少得几朵小红花？

活动要求：（1）算一算：列式计算每一道题目；

（2）比一比：以上这三道题目有什么相同点或不同点；（3）说一说：和同桌说说你是怎么想的。

预设1：这三题都是用减法算式11-6=5去解决的。

明确：11-6=5这个算式可以解决不同的问题。

预设2：第二题和第三题都是用括线解决问题。

明确：不管是求括线上面的左边部分，还是求括线上面的右边部分，都是求一部分，都可以用减法来计算。

预设3：第一题是求相差多少，第二题、第三题是求一部分，都用减法计算。

小结：不论是求相差数还是求一部分，都是用减法计算的。不论是动态情境中飞走的一部分，还是静态情境中的一部分，也都用减法去计算。

2.我会编

提问：上面这些问题都是用11-6去解决的，11-6还能解决生活中的哪些问题呢？请你独立编题，再和同桌说一说。

“我会比”呈现了三种减法计算的问题情境，再加上二年级上册的“已知大数与相差数，求小数需要用减法计算”，囊括了小学阶段所有用减法计算的问题。教学时，教师将问题整体呈现在学生面前，学生自然从整体上认识了用减法解决的所有问题结构。由此，感悟到减法算式的模型，破除一式单题的思维定式。

“我会编”环节中，教师让学生通过自主编题同类结构进行内化，在正逆交互中形成算式的模型结构，同时也破除了一式单题的思维定式。

四、整合资源，拓展模型

教材是教学的重要依据，但其资源是有限的。因而在教学活动中，一线教师应该学会精心整合教育资源，根据学生学情设计有层次、有内涵、形式丰富的练习。由此，让学生在练习中获得数学模型，巩固数学模型，拓展数学模型。

[情境四]差不变，巧解题

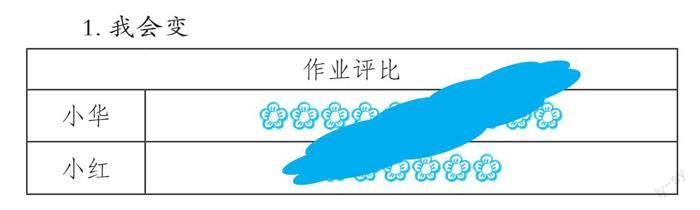
1.我会变

提问：这张作业评比图不小心被弄脏了，只知道小华和小红的红花朵数相差5朵，那么小华、小红分别可能有几朵？

追问：其实“差不变”的规律就体现在这张图上，当小华和小红各增加1朵，他们相差5朵，各增加2朵，他们相差也是5朵，各增加10朵呢？100朵呢？1000朵呢？只要增加或减少相同的朵数，他们的差都是不变的。

明确：观察下面直方图发现，第一个直方图是被减数，第二个直方图是减数，相差的部分就是它们的差。被减数和减数分别增加或减少相同的数，差是不变的。

接着刚才的11-6=5，在这里是解决第一行的11朵花比第二行的 6 朵花多5朵。根据上面的问题情境，小华和小红分别可能有几朵？这样自然过渡，引出这一环节的练习，学生通过思考得出一系列的式子：12-7=5，13-8=5，14-9=5。这样以一题带出一组式子，达到结构化的训练效果。

2.我会思

出示题目：哥哥今年12岁，弟弟今年5岁，他们相差几岁？

提问：那去年呢？明年呢？20年后呢？

追问：他们为什么都相差7岁呢？

预设：哥哥长大，弟弟也跟着长大，他们永远都是相差7岁。

小结：这是利用“被减数和减数同时增加或减少相同的数，差不变”的规律来解决问题，生活中处处蕴含着数学知识。

上述练习题的设计遵循从易到难、从具体到抽象的原则，“我会变”和“我会思”巧妙地将数学知识与生活实际紧密相连，选取了常见的生活场景，充分调动学生的积极性，让学生明白数学模型的运用不仅可以解决数学问题，还可以解决生活中遇到的各种问题，巩固所学知识，增强了学生运用模型的意识。