某火炮药协调器多学科耦合模型参数辨识与可靠性分析

石志杰，陈龙淼，羊柳，刘太素

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.南京工程学院，江苏 南京 211167)

弹药自动装填系统在火炮武器系统中负责弹丸、模块药的存储补给、记忆识别,自动选择弹丸类型、装药种类及药块数量[1],并进行任意角度下的装填动作。药协调器作为自动装填系统的重要子部件,主要功能是接收从自动化药仓中分出的药块,随后绕耳轴回转将药块协调至指定射角的输药位,其协调到位精度和协调运动时长直接影响着火炮的射击状态和射速,如果协调的定位误差超出了规定的精度指标,则会影响到发射任务的完成[2]。

机构动作可靠性的定义[3-6]为在规定的时间内和规定的条件下,机构完成规定功能的能力。相应的,机构可靠度定义为机构完成规定功能的概率。机构可靠性的研究最早源于零件运动副磨损问题,经过几十年的发展,可靠性预计和建模方法大致可分为纯概率方法、近似概率方法和非概率方法[7]。在纯概率方法中,蒙特卡洛模拟(Monte Carlo Simulation,MCS)作为一种经典的随机抽样数值仿真方法,是可靠性分析问题成熟有效的解决手段。

使用MCS对系统模型进行可靠性分析,能够减少试验工作量,但前提应保证仿真模型的准确性,模型对外部输入的响应量要与实际系统相吻合。然而,待研究系统的内部特性往往不能得到全部认识,这时就需要针对不确定参数辨识建模。系统辨识就是在一组模型类中选取一个与数据拟合得最好的模型[8]。近年来,在经典辨识方法的基础上发展出了一些新的参数辨识方法。赵旭宝等[9]基于改进PSO算法对弹性胶泥缓冲器动力学模型各参数进行了优化求解。赵抢抢等[10]以时序曲线相似度为目标函数,使用差分进化算法对研究对象的区间不确定参数进行了辨识。武诗睿等[11]提出了一种基于摩擦-速度曲线特定区域形状分析的LuGre摩擦参数辨识法,辨识实验量更小精度更高。

此外,围绕火炮自动装填系统的可靠性问题已经存在较多研究。高学星[7]将自动装填系统中的常见故障以概率形式抽象为模型的不确定性参数,创建了基于径向基函数神经网络的代理模型,提高了装填系统可靠性的计算效率。曹汝男[12]提出一种新的主动学习方法,兼顾失效概率的估计精度,提高了复杂机械结构的可靠性分析效率,并将其运用到火炮协调器的定位精度可靠性分析中。杨丽[13]考虑某双路供弹系统的动作特性,分析了供弹机构可靠性,研究了针对自动火炮关键性能的评估策略。

笔者在考虑柔性体和运动副间隙的前提下,建立了某火炮药协调器刚柔耦合动力学模型和控制模型。针对系统中的区间不确定参数,使用随机惯性权重的粒子群算法,结合试验数据对系统参数进行辨识,同时设计仿真试验研究此方法的有效性和辨识精度。在利用辨识参数验证仿真模型的准确性后,使用该模型对药协调器不同工况下的动作可靠度进行估计,同时得到各尺寸参数对定位误差的影响程度,为药协调器的可靠性设计提供参考。

1 某火炮自动装填系统药协调器模型

1.1 药协调器结构组成

药协调器的结构组成包括耳轴连接盘、协调电机、减速器、协调臂和调姿电缸组件等,自动输药机安装在协调臂末端的调姿轴上。图1为药协调器和输药机的结构示意图。

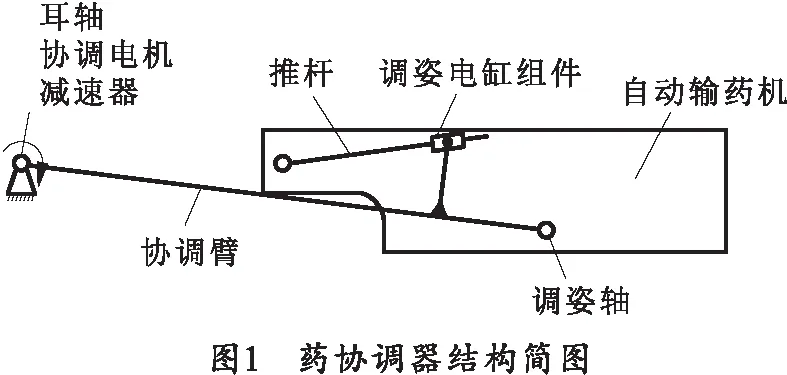
输药时,在调姿电缸组件的驱动下输药机可以绕调姿轴做18°的调姿运动,上下极限位置都有机械限位,分别对应接药姿态和输药姿态(图1为输药姿态),同时输药机还随协调臂一起绕耳轴回转作协调运动。药协调器通过调姿和协调两个动作,配合完成输药机轴线在任意高低射角下与炮膛轴线对齐的输药功能。由此可知,输药机自水平接药位协调至目标射角输药的过程中,药协调臂的实际转动角度值为射角加调姿角(18°)。

总体来看,药协调器动作可靠性的影响因素主要包括以下几点:

1)药协调器的协调臂、限位块、推杆等构件在制造过程存在的尺寸误差、形位误差,以及在装配和焊接时产生的间隙和变形,都一定程度上影响了协调器的到位精度。

2)协调臂的变形。药协调器是在高速、重载的条件下工作的,这个过程中其主体协调臂会产生变形,影响动作的可靠性。

3)控制系统的驱动误差。控制系统的输出误差较大,抗干扰能力不强,规定时间内电机无法驱动部件到达理论位置,也会降低药协调器的动作可靠性。

1.2 药协调器刚柔耦合的动力学模型

为了研究协调过程,基于药协调器的工作原理,作出如下假设:

1)除协调臂外,所有部件均假定为刚体,不考虑载荷及构件变形影响。

2)协调过程中耳轴和炮尾固定不动,忽略车体的姿态扰动。

3)输药机限位块与协调器碰块之间、各组转动副轴孔之间的碰撞为弹性碰撞。

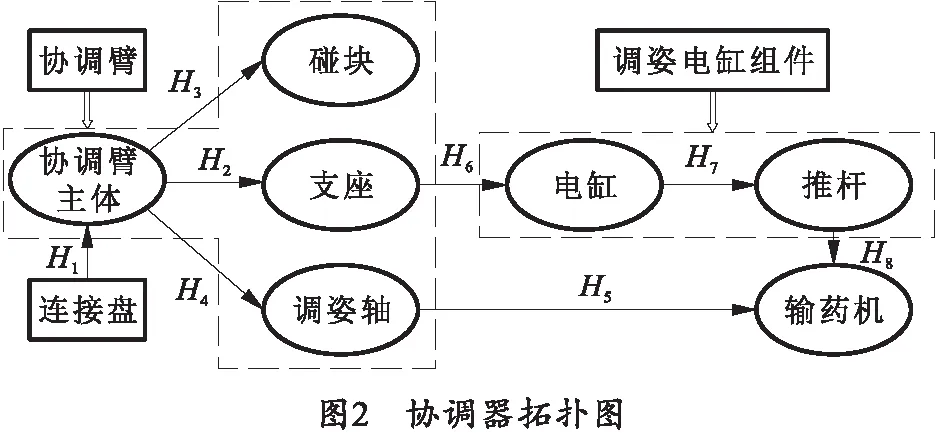
将装配好的药协调器三维模型导入ADAMS中,根据实际的物理约束情况添加运动副,并定义了接触关系,拓扑图如图2所示。其中,H2、H3、H4为固定约束,H1、H5、H6、H8为旋转约束,H7为平移约束,调姿驱动力简化为H7运动方向的单向力。

由于在协调过程中,协调臂会发生弹性变形,因此模型需要考虑柔性体构件对协调器动作可靠性产生的影响。协调臂主体由耳轴挂套、连接加强筋、堵块以及钢板焊接而成,耳轴挂套采用实体单元进行离散,折臂部分采用壳单元进行离散,并参考实际约束副建立外连节点和刚性区域。协调臂结构材料属性如表1所示,有限元离散模型如图3所示。

表1 协调臂结构材料属性

提取前12阶模态输出协调臂的模态中性文件,替换原先的刚体模型并重新添加相关约束,建立刚柔耦合的药协调器模型。

1.3 药协调器PID控制联合仿真

在药协调器中,上位机发出指令给驱动器,通过电流控制电机的转矩,经过减速器后驱动协调臂进行绕轴动作。编码器实时反馈协调臂当前角度给驱动器调整控制量,形成一个完整的闭环控制系统。根据这一实际工作情况,定义协调臂在回转耳轴处所受的驱动力矩为

T=KT·iq·i·ξ,

(1)

式中:KT=300 N·mm/A,为电机的转矩常数;iq为电机q轴电流;i=128,为协调减速器的传动比;ξ为协调减速器的传动效率。

摩擦是一种复杂的非线性物理现象[14],是机械伺服系统的主要阻尼来源,对药协调器的控制性能影响很大。在协调运动时,由于减速器的存在以及一些未知的阻尼特性,用试验样机驱动器输出的电流去控制药协调器的动力学模型会发生严重的超调现象。由于ADAMS内置的摩擦模型始终不能很好地贴合试验数据,笔者选择库仑-黏性摩擦模型[14-15]来建立较为准确的动力学模型。药协调器工作时的摩擦力矩定义为

(2)

式中:θ为角位移;Kv>0为黏性摩擦系数;Kc>0为库仑摩擦力矩;sgn(·)是符号函数。

为了在运动过程中速度过渡平滑、减小冲击,药协调器选用如图4所示的七段式S形速度曲线规划法建立理想运动轨迹(以目标射角60°为例)。控制模型采用PID控制器,PID控制器按偏差的比例(P)、积分(I)和微分(D)进行控制,因其原理简单、调参方便、易于实现等优势,被广泛应用于工业控制过程中[16]。

规定电流为机械系统输入变量,角位移及其他状态量为输出变量,导出药协调装置的动力学模型,搭建如图5所示的PID联合仿真控制模型。

2 参数辨识与模型验证

2.1 药协调器参数分析

由1.2节建模过程可知,药协调器模型包含较多参数,其中一些参数可以通过测量和计算获得,还有一些参数则是不确定的。考虑设备精度和加工方式对构件尺寸的影响,药协调器各组转动副的轴孔尺寸服从表2的设计公差。

表2 药协调器运动副配合列表

为了研究表2中各组转动副的间隙和尺寸分布,需要在1.2节建立的药协调器动力学模型的基础上作一些调整。首先,建立表中各转动副处轴孔的参数化模型,再用平面约束结合接触力的方式分别替换掉原先的理想旋转约束。此外,黏性摩擦系数Kv、库仑摩擦力矩Kc和减速器传动效率ξ这些模型参数也是未知的,且难以在试验中直接测量得到。事实上,即便是单个产品在一次动作过程中这些参数也是变化的,考虑到协调定位的时间很短,可以近似地把它们看作定值,并用试验数据辨识获得。不同产品之间的上述参数虽然也存在波动,但在实际设计和制造过程中并不能提前估计和人为干预。因此笔者利用辨识参数进行可靠度计算,分析设计尺寸对药协调器可靠性的影响,以指导生产实际。

2.2 基于随机权重粒子群算法的参数辨识方法

根据前文建立的药协调器动力学模型,每给定一组不确定性参数(Kv,Kc,ξ),模型在实际控制器电流的驱动下就会得到一条角位移的仿真曲线,与试验曲线最为吻合的仿真曲线所对应的就是最优的一组参数。也就是说,药协调器的参数辨识问题可以被认为是一个优化问题。

在仿真角位移曲线的时间轴上等距选取m个时间点(t1,t2,…,tm),并将每个时间点处的角位移θ与实际角位移θ*的差值取绝对值,把它们和的最小值作为优化目标,即目标函数计算公式为

(3)

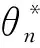
目标函数的寻优采用基于随机惯性权重的粒子群算法(Particle Swarm optimization,PSO),因其容易理解、精度高、收敛快,该算法在许多优化问题中得到成功应用。在PSO中,每个粒子都可以看作是优化空间内的一个解,都有一个由目标函数决定的适应度值,算法从随机解出发迭代寻找最优解。每次迭代中,粒子会跟踪本身找到的历史最优解(个体极值)和整个种群目前找到的最优解(群体极值)来更新自己的位置,公式如下[17-18]:

(4)

(5)

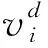
为了改善算法迭代初期的局部搜索能力和迭代后期的全局搜索能力,避免其陷入局部最优[19],采用随机惯性权重的改进粒子群算法。随机惯性权重w的生成公式为

w=μmin+(μmax-μmin)×rand(0,1)+σ×N(0,1),

(6)

式中:μmin和μmax分别代表随机惯性权重的最小值和最大值;rand(0,1)表示[0,1]均匀分布随机数;σ表示标准差;N(0,1)表示正态分布的随机数。

综上,辨识药协调器不确定性参数的流程图如图6所示。

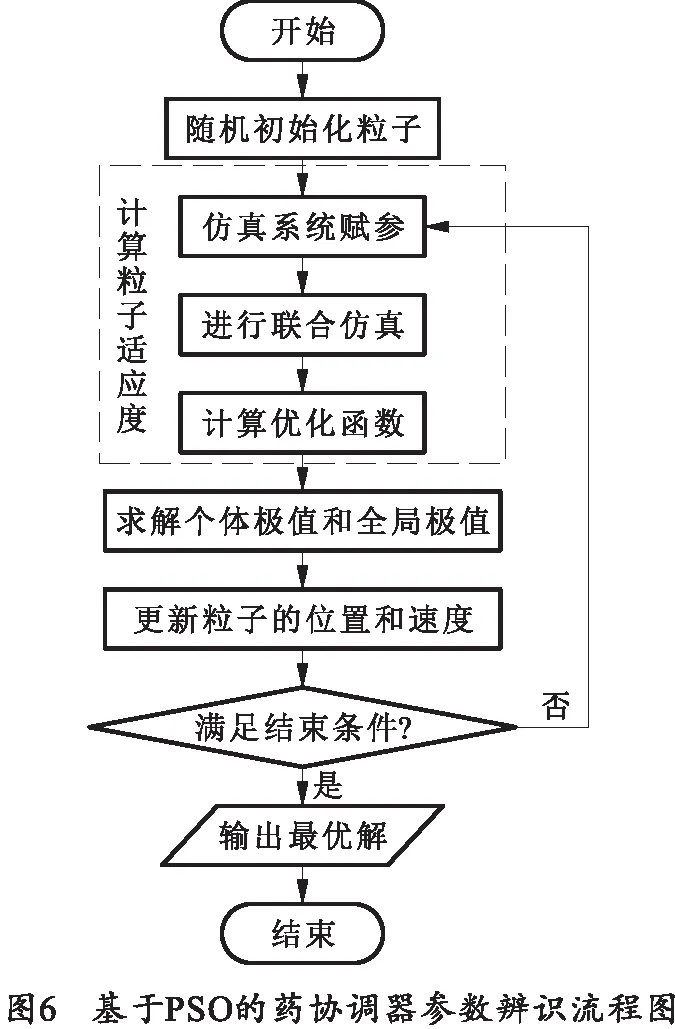
2.3 药协调器的参数辨识

根据工程经验、产品说明书和相关文献,确定待辨识参数的搜索范围分别为:黏性摩擦系数Kv∈[50,350],单位N·m·s·rad-1;库仑摩擦力矩Kc∈[200,800],单位N·m;减速器传动效率ξ∈[0.75,0.95]。

为了检验2.2节的方法辨识药协调器参数的精度,笔者设计了几组仿真试验,表3给出了辨识结果。结果表明,在仿真试验中,药协调器3个待辨识参数值的平均辨识误差分别为0.77%、1.24%和0.13%,辨识精度良好。

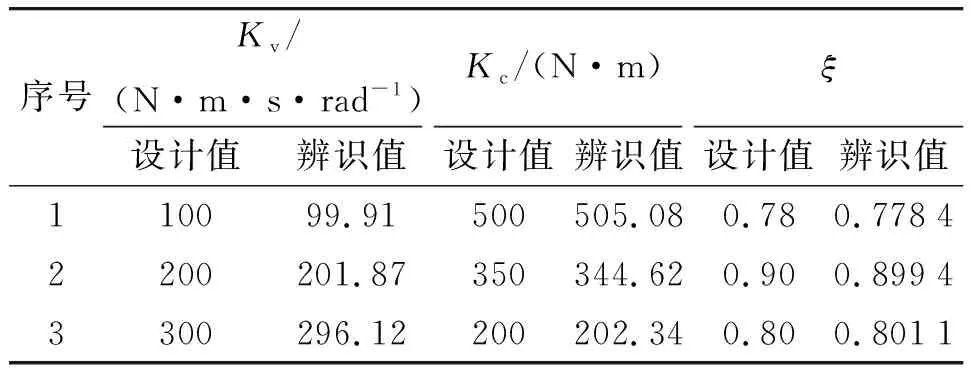
表3 仿真试验数据辨识结果

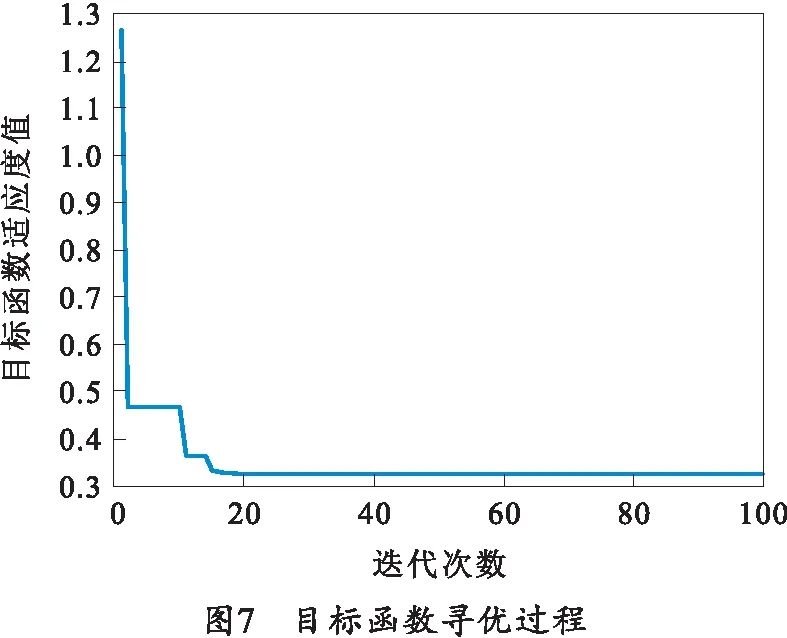
选择6块药装填、药协调器从接药位协调到30°射角的工况,对试验样机台架进行数据采集,获得电流和角位移数据进行参数辨识。目标函数寻优变化过程如图7所示,可以发现适应度值在迭代一定次数后趋于收敛,但不为0,这是因为样机试验还受到多种外界因素的干扰。

在重复性协调试验后,共选取3组电流和角位移数据进行了参数辨识,如表4所示,并将3次试验结果的均值作为最终的辨识值。

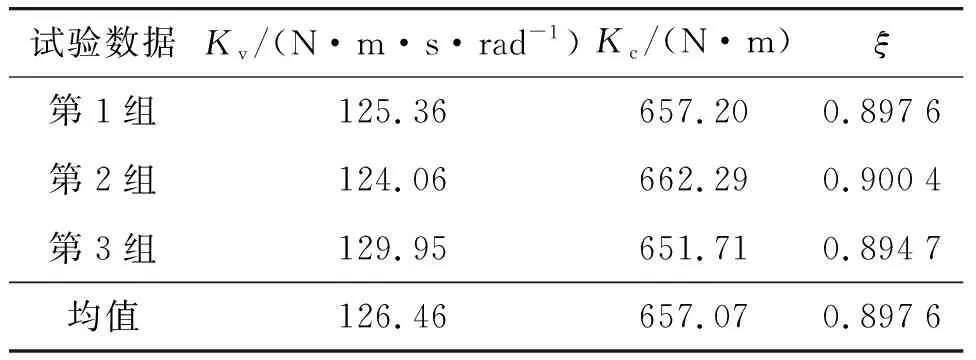
表4 样机试验数据辨识结果

将参数的辨识值代回仿真模型后,另取一组试验数据作为对照组,对比仿真角位移曲线和试验角位移曲线,如图8所示。可以看到,二者具有很高的相似度,这说明辨识结果是合理的,与试验情况相吻合,达到了工程需要。

3 药协调器动作可靠性分析

3.1 可靠性功能函数

药协调器的动作可靠性受尺寸参数、外部载荷、环境变量等多种因素的影响,这些因素可以设为系统的随机变量X=(x1,x2,…,xn),则装置的输出响应函数为

Y=D(X)=D(x1,x2,…,xn).

(7)

已知理想情况下药协调器的输出响应为Y*,Y*是确定工况下的一个给定值,由此可得系统的输出误差为

δ=Y-Y*.

(8)

(9)

式中:当Z>0时,表示药协调器的运动可靠;当Z=0时,表示机构处于临界失效状态;当Z<0时,机构处于失效状态。

因此,药协调器动作失效概率为

(10)

式中,fδ(·)为输出误差δ的概率密度函数。

3.2 可靠性数值估计

由于柔性体的存在、控制系统的误差和其他外部随机扰动,难以得到式(9)中药协调器显式的可靠性功能函数,为此笔者使用MCS对药协调器的动作可靠度进行估计。

假设各轴孔尺寸参数服从正态分布,均值由基本尺寸和设计公差决定,标准差根据3σ原则确定,具体取值如表5所示。通过Isight内置的Monte Carlo模块,对药协调器的模型参数进行描述抽样(Descriptive Sampling)。

表5 各尺寸参数的均值与标准差

描述抽样是将每一个随机变量所定义的空间分为相等的概率子空间,对每一个随机变量子空间的分析只进行一次[20],可以在不影响结果的前提下极大地减少抽样点数量。药协调器动作的允许误差极限阈值为±0.18°,在装填6块药、射角30°和60°两个工况下,分别对各尺寸参数进行1 000次抽样,得到药协调器的动作可靠度为99.8%和99.9%,协调定位误差的频数分布直方图及累积概率分布图分别如图9、10所示。

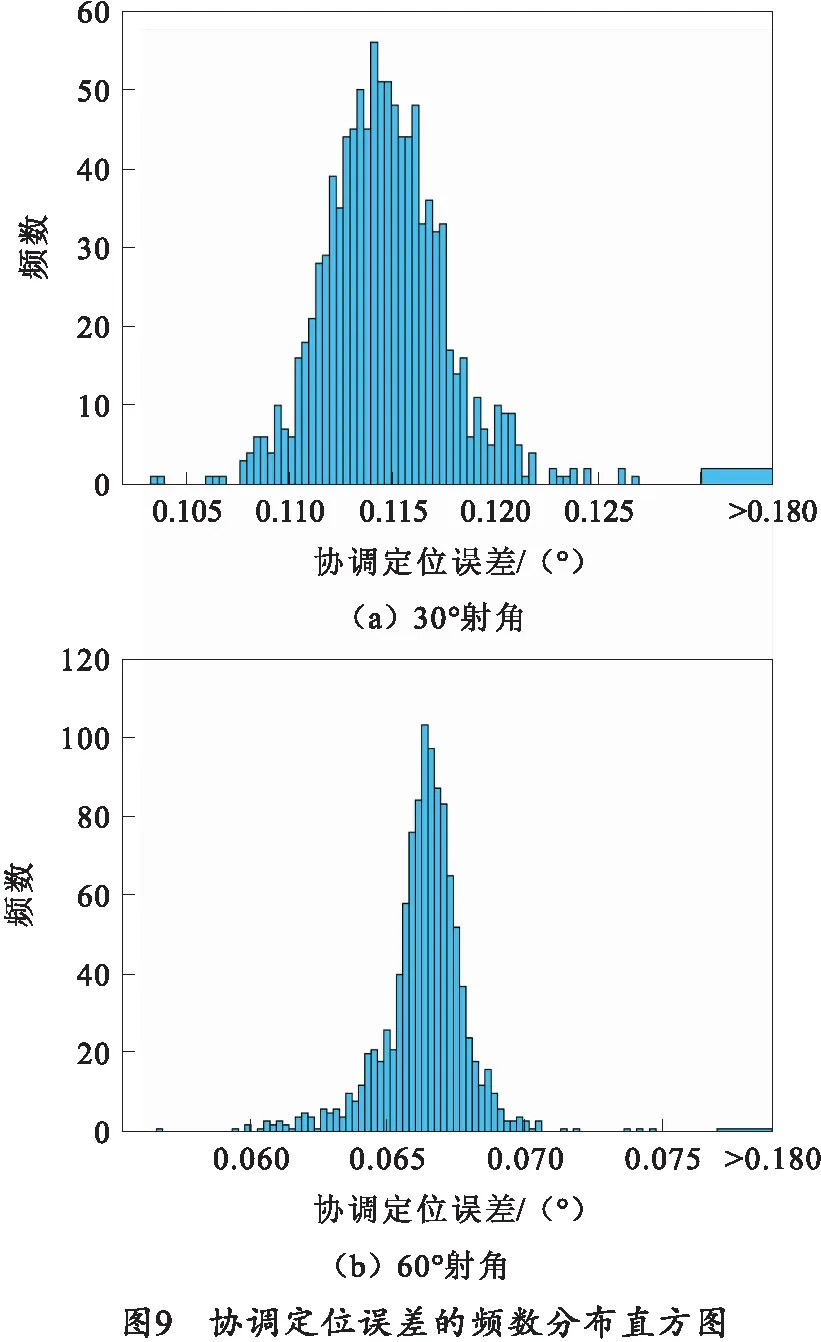
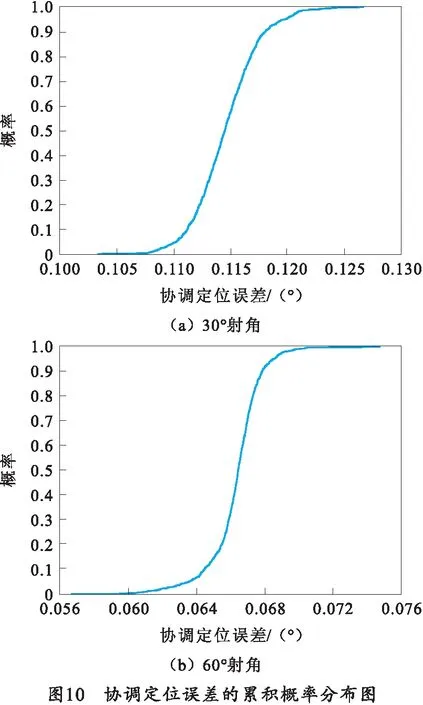
可以看到,考虑协调臂柔性后,实际协调角度有偏大的趋势,协调定位误差的整体分布向x轴正方向偏移。由于30°射角较60°射角时协调器负载对耳轴处的力矩更大,而装填的时序要求却缩短了,因此,60°射角的协调定位误差整体要小于30°射角,分布也更为集中,可靠性表现总体上优于30°射角。

在MCS模块里,失效率的影响因素可以通过软件后处理中的Pareto图表示,如图11所示。可以看出,30°射角时调姿轴转动副的间隙大小对协调器失效率的影响贡献最大,而60°射角时则是电缸支座转动副的间隙大小影响最大,二者与失效率均为正相关。

4 结束语

笔者建立了某火炮药协调器刚柔耦合动力学模型和控制模型,分析了药协调器动作可靠性的影响因素。基于随机惯性权重的粒子群算法,根据试验数据辨识系统中的参数并验证了仿真模型的准确性,也表明了该辨识方法的可行性。在考虑柔性体、控制误差和运动副间隙的条件下,对药协调器动作可靠度进行了估计。通过MCS得到在装填6块药、协调角度30°和60°的工况下,药协调器动作可靠度为99.8%和99.9%,总体失效概率较小。本文研究结果对类似结构自动装填系统的设计和可靠性分析具有一定的借鉴意义。