基于正弦函数的液冷板上流体流向对锂离子电池散热性能的影响

2023-08-29唐程波锁要红何昭坤

储能科学与技术 2023年8期

唐程波，锁要红，何昭坤

（福州大学机械工程及自动化学院，福建福州 350108）

电动汽车由于节能减排效果良好而备受关注[1]，其动力源为动力电池。与其他动力电池相比，锂离子电池在能量、动力密度、耐用性和安全性等方面均具有优势，是电动汽车的主要动力源[2-7]。但是锂离子电池在服役过程中产生大量的热，造成电池组温度升高(温升)，可能引发燃烧或者爆炸等。这不仅严重影响了锂离子电池的使用寿命，更造成财产损失及危害人的生命安全等问题[8-10]。

针对锂离子电池服役过程中的温升现象，目前采用的散热方式主要有空冷、液冷、相变冷却和热管冷却[11-13]。液冷因其良好的散热冷却效果受到越来越多电动汽车厂家青睐[9,14-16]。Karthik等[17]提出了多通道U形液冷板，采用多目标优化技术并结合计算流体动力学进行温度场模拟，获得了多通道中冷却剂的最佳质量流率组合。Amalesh 等[18]研究了7种不同结构的多通道液冷板(矩形槽、方波形、低波形、正弦波、弧形、圆槽和锯齿形)对电池冷却性能的影响。Monika等[19]用三维数值方法对6种不同的微通道(蛇形、U形、直形、南瓜形、螺旋形和六角形)进行对比分析，其中U形和蛇形是多通道，并根据压降、温度变化、无量纲因子j/f、平均温度以及均匀性因子对电池冷却性能的影响进行评估。以上文献研究了多通道对电池散热性能的影响，但流体流向对电池散热性能的影响未做探讨。

张继龙等[20]研究了流道面积、流道位置及流体流向对多蛇形变结构流道冷却板模型散热性能的影响，发现逆流流道能降低冷却板温度标准差。Sheng等[21]研究了冷却板中流体流向、质量流率和通道宽度对单个电池温度分布的影响，发现入口位置、出口位置以及流体流向对电池温度分布和冷却板功耗比有很大影响。Huo 等[22]对6 道直流道进行了流体流向的研究，指出改变流体流向可以改善电池温度的均匀性。以上文献研究了固定放电倍率、入口温度和入口流速下流体流向对电池散热性能的影响，实际上不同放电倍率、不同入口温度和不同入口流速下流体流向对电池散热性能也有重要影响。

基于以上问题，本工作以最高温度、温度均匀性、温度一致性和压降为评价指标，设计了一种正弦函数液冷板流道，利用COMSOL 软件分析正弦7 流道液冷板上流体流向对锂离子电池散热性能的影响并探讨不同放电倍率、入口温度和入口流速下电池散热性能(最高温度、温度均匀性和温度一致性)随流体流向变化的规律。

1 模型建立

如图1(a)所示，本工作选用方形锂离子电池，每5块锂离子电池放入一块液冷板(MCP)，锂离子电池尺寸为180 mm×100 mm×14 mm，液冷板尺寸为180 mm×100 mm×6 mm[23]。为了提高液冷板的散热效率，本工作设计了一种正弦函数流道{6 sin[(2/13)x]}进行冷却[图1(b)]，流道数量为7，流道宽度为6 mm，流道深度为3 mm。由于模型对称，仅取一半进行研究，如图1(b)所示。靠近液冷板的电池编号分别为B1、B2和B3。锂离子电池、液冷板和冷却液的热物理性能列于表1中。

表1 锂离子电池、液冷板和冷却液的热物理性能Table 1 Thermophysical properties of the lithium ion battery, liquid cooled plate and coolant

图1 电池组及设计的正弦冷却流道Fig.1 Battery pack and designed sine cooled channel

1.1 控制方程

假设流道内的流体为不可压缩流体，则连续性方程[18]为：

不考虑流体自身的重力影响，则动量守恒方程为：

流体、液冷板和电池的能量守恒方程分别为：

方程(2)～(5)中下标w、c和b分别表示水、液冷板和电池；μ、ρ、T、Cp、k、ν和P依次为动力黏度、密度、温度、比热容、导热系数、速度和压强；Q̇gen为电池的产热率，放电过程中其表达式[23]为：

式中，A1、A2、…、A7为常数，取值列于表2中。

表2 方程(6)中1 C、2 C和3 C的多项式系数[24]Table 2 Polynomial coefficients for 1 C, 2 C and 3 C in equation (6)[24]

温度标准差S被用作电池之间温度综合非均匀性指标以进一步比较温度分布。其值越小，电池组温度的一致性越好。为了探讨电池散热性能，分别引入温差ΔT和温度标准差S来描述单个电池的温度均匀性和电池组温度一致性，其表达式如下：

其中n为电池个数，ΔTi为第i个电池的温差，ΔTˉ为n个电池温差的平均值。

1.2 初边界条件

假设电池的初始温度为298.15 K；流体入口流速ν0为0.1 m/s，流体入口温度T0为298.15 K，流体出口相对压强P0为0 Pa，流道与流体交界处为无滑移边界，其他边界为绝热边界。

2 数值仿真与讨论

选水作为冷却液，正弦流道的最大水力直径Dh为4 mm。由于流体入口流速ν0为0.1 m/s，所以雷诺数Re=554.94<2300，故流道内流体的流动为层流。下面选用COMSOL 有限元中的层流与固体和流体传热耦合模块进行仿真分析。

为了确保计算结果的准确，以流体同向流动模型为例，通过整体电池最高温度和压降对网格进行独立性验证。网格数量分别设置为116773、228536、609200、965733、2014391 和2368228，所得电池最高温度Tmax和压降ΔP随网格数量的变化规律如图2所示。当网格数量大于2014391，电池最高温度和压降变化小于1%，趋于稳定。因此，网格数为2014391时仿真结果的准确性能得到保证，故本工作模拟选用网格数为2014391 进行仿真。此外，由于B1电池温度变化较为明显，故后续研究选择B1电池的最高温度、温差、电池组温度一致性以及压降为散热性能指标，且流道内流向的变化通过设计的4 种方案来表达(如图4 所示)。需要特别指出的是：这4种方案表示了流体流向交错改变的次数(交错流次数)，相邻流道流体流向不同即交错流次数记1次，这样方案1～4的交错流次数依次为6、4、3和2次。

图2 网格独立性验证Fig.2 Grid independence verification

2.1 正弦流道与直流道对电池散热性能的影响

图3为正弦流道与直流道B1电池的温度分布云图。显然，正弦流道的高温区域(红色)小于直流道的高温区域。正弦流道与直流道相比增大了电池与流道内流体对流换热的接触面积，由Q=hA(tw-tf)可知对流换热的热流量Q随A的增大而增大，这样电池中更多的热流量进入正弦流道，进而电池温度降低。此外，相比于直流道，正弦流道的T1max从28.8 ℃下降到28.5 ℃，下降了0.3 ℃；ΔT1从3 ℃下降到2.8 ℃，下降了0.2 ℃。这些表明正弦流道的散热效率更高。

图3 正弦流道 (a) 与直流道 (b) B1电池的温度分布Fig.3 Temperature distribution of B1 battery in sine channel (a) and straight channel (b)

2.2 正弦流道频率与振幅对电池散热性能的影响

为了探讨正弦流道频率和振幅对B1 电池散热性能的影响，图4(a)和(b)分别为B1 电池在不同频率下和不同振幅下的最高温度T1max和压降ΔP。显然，最高温度随着正弦流道频率的增大而减小，这说明增大正弦流道的频率有利于电池散热；然而，频率为4/26后压降上升幅度增大，如图4(a)所示，因此选择频率为4/26较为合适；选择低振幅时更有利于B1电池散热，这是因为如图4(b)所示，B1电池的最高温度和压降均随振幅的增大而增大。这样低振幅更有利于电池散热，故后面计算选择振幅为6。

图4 频率 (a) 与振幅 (b) 对B1电池散热性能的影响Fig.4 Influence of frequency (a) and amplitude(b) on heat dissipation performance of B1 battery

2.3 不同放电倍率下电池散热性能随正弦流道内流体流向的变化规律

放电倍率与放电过程中电池产热正相关，即放电倍率越大产热也越大，这样电池温度也会越高。因此，为了研究不同放电倍率下正弦流道内流体流向对电池散热性能的影响，设计了如图5 所示的4 种流体流向来考察B1电池的散热性能。

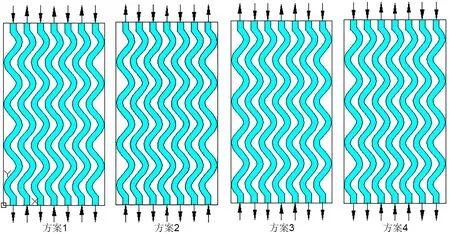
图5 四种流体流向方案Fig.5 Four flow direction of fluid schemes

图6(a)给出了最高温度T1max的变化规律。显然，所有方案与同向相比，T1max都有所下降，且T1max下降的幅度随着放电倍率的增大而增大，这说明流体流向对电池散热的影响随着放电倍率的增大而增大。以方案1 为例，与同向相比，1 C 放电倍率时方案1的最高温度下降了0.51 ℃，而3 C放电倍率时下降了2.3 ℃，是1 C时的451%。此外，方案1在各放电倍率下的T1max都是最低的，且在3 C放电倍率下对电池散热提升最大。

图6 不同放电倍率下电池散热性能 (a) 最高温度、(b) 温差、(c) 温度标准差和 (d) 压降随流体流向的变化规律Fig.6 The variation of heat dissipation performance (a) maximum temperature, (b) temperature difference, (c)standard deviation of temperature and (d) pressure drop with flow direction of fluid at different discharge rates

图6(b)为在不同放电倍率条件下，同向和4 种方案的B1电池温差ΔT1的变化规律。所设计的四种方案与同向方案相比，ΔT1都有所下降，且ΔT1下降的幅度随着放电倍率的增大而增大，这说明流体流向对电池温度均匀性的提升随着放电倍率的增大而增大。此外，随着交错流次数增多，流体流向对B1电池温度均匀性的提升越来越大，这是由于随着交错流次数增多，交错流流道之间的换热次数增多，使得每个流道带出的热量更均匀，进而B1 电池温度均匀性的提升显著。以3 C放电倍率为例，交错流次数为2 次的方案4 温差比同向方案的温差下降了2.88 ℃，而交错流次数为6次的方案1温差比同向方案的温差下降了6.12 ℃。与同向相比，方案1在3 C放电倍率条件下温差下降得最多，为6.12 ℃。

如图6(c)所示，除了方案4 在1 C 和3 C 条件下的温度标准差S略高于同向的S，其他方案相比于同向S都有下降。此外，S随着交错流次数的增大而减小，这说明高交错流次数有利于电池组的温度一致性，但交错流次数达到一定次数时对电池组的温度一致性提升是有限的。例如，在3 C放电倍率下的方案1和方案2，交错流次数为6次的方案1和交错流次数为4 次的方案2 的S由同向的3.61 分别下降到3.28 和3.33，方案1 和方案2 的S仅相差0.05。S随着放电倍率的增大而增大，这说明高放电倍率不利于电池组的温度一致性，而高放电倍率下的方案1能最大程度地改善电池组的温度一致性。

各方案的压降见图6(d)，可以发现：4 种方案的压降与同向流动的压降相比略微升高，但最大压降仅升高了6 Pa，这样流向改变对能量损耗的影响可以忽略。此外，压降不随放电倍率的变化而变化，这是由于动力黏度μ假设与温度无关，取定值。综合最高温度、温差、温度标准差和压降来看，3 C放电倍率下方案1最大程度地改善了电池的散热性能。

2.4 不同入口温度下电池散热性能随正弦流道内流体流向的变化规律

图7 给出了3 C 放电倍率时不同入口温度下流体流向对电池散热性能的影响。各方案和同向的B1 电池最高温度T1max的变化如图7(a)所示。各方案的T1max比同向都降低了，其中，方案1和方案2的T1max下降得最多，且T1max随着入口温度的增大而增大，这是因为入口温度越高，流体与电池的温度差越小，热传导越慢，进而电池温度较高。随着入口温度的变化，同一种方案的T1max下降幅度几乎没有变化，这说明流体流向对最高温度的降低不受入口温度的影响。

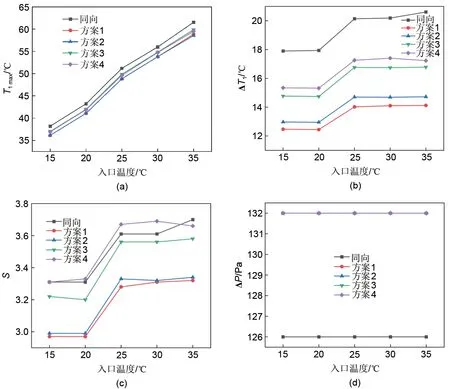
图7 不同入口温度下电池散热性能 (a) 最高温度、(b) 温差、(c) 温度标准差和 (d) 压降随流体流向的变化规律Fig.7 The variation of heat dissipation performance (a) maximum temperature, (b) temperature difference, (c)standard deviation of temperature and (d) pressure drop with flow direction of fluid at different inlet temperature

3 C放电倍率下同向和各方案的B1电池温差随入口温度变化的关系如图7(b)所示。从图中观察到：各方案的B1电池温差ΔT1都比同向流动的电池温差低，这说明交错流动有利于提高电池温度均匀性。当流体入口温度为15 ℃和20 ℃时，ΔT1较低；然而入口温度大于20 ℃时，ΔT1明显增大，这是由于入口温度越高，流体流动带出去的热量越少，距离流体近的电池温度上升较慢，远的电池温度上升较快，进而造成温差增大。入口流体温度为25 ℃和35 ℃方案1的ΔT1下降最多，但入口流体温度为35 ℃时大于环境温度25 ℃，不利于电池散热。因此，入口流体温度为25 ℃时方案1 对电池温度均匀性提高最大。

图7(c)为温度标准差S随入口流体温度的变化关系，仅有方案4 比同向的S高。在入口温度为15 ℃和20 ℃时，S较低，而入口温度大于20 ℃时，S较高。与同向相比，方案1 的S下降最多。在20 ℃和35 ℃时，同向的S分别为3.31和3.70，而方案1 的S为2.97 和3.32，分别下降了0.34 和0.38。但入口温度为35 ℃时大于环境温度25 ℃，不利于电池散热。因此，入口温度为20 ℃时方案1对电池组的一致性提高最大。此外，入口温度为25 ℃时S下降了0.33，与入口温度为20 ℃时相差不大。结合最高温度、温差和温度标准差来看，在方案1情况下，入口温度为25 ℃时，电池散热最佳。此外，图7(d)显示压降不受入口温度影响。

2.5 不同入口流速下电池散热性能随正弦流道内流体流向的变化规律

图8(a)为不同入口流速下流体流向对电池最高温度的影响，各方案的T1max都比同向的低。随着入口流速的增加，各方案的T1max都下降且T1max下降得越来越慢，而压降[如图8(d)所示]增大得越来越快，这是由于随着入口流速的增大，流体带出去的热量增多，从而造成电池温度下降，而流体与电池热交换的时间减少，造成电池温度下降越来越慢；压降与流速平方成正比，故压降增大越来越快。因此，入口流速增大到一定数值时，对提高电池散热性能是有限的。

图8 不同入口流速下电池散热性能 (a) 最高温度、(b) 温差、(c) 温度标准差和 (d) 压降随流体流向的变化规律Fig.8 The variation of heat dissipation performance (a) maximum temperature, (b) temperature difference,(c) standard deviation of temperature and (d) pressure drop with flow direction of fluid at different inlet velocity

3 C 放电倍率下同向和各方案的B1 电池温差ΔT1随入口流速的变化规律如图8(b)所示。各方案的ΔT1相比于同向都有减小。方案1的ΔT1在不同入口流速下都是最低的，且当入口流速大于0.1 m/s时，ΔT1下降的幅度已经很小，而压降增大得越来越快。同向与各方案的ΔT1之差随着入口流速的增大而减小，这说明高流速下流体流向对电池温度均匀性的提升是受到限制的。因此，从电池温差来看，入口流速增大到一定程度时对电池温度均匀性的影响也是有限的。

图8(c)为电池在不同入口流速下的温度标准差S，针对不同的入口流速，仅有方案4 在高流速下的S比同向的S高，这说明方案4 在高流速下不利于改善电池组的温度一致性。S随着入口流速的增大而增大，因此，高流速下不利于改善电池组的温度一致性。此外，方案1 能最大程度地减小S。从最高温度、温差、温度标准差和压降来看，方案1更有利于电池散热，且在入口流速为0.1 m/s 时电池散热和能量损耗最优。