考虑电动汽车灵活储能的微电网双重激励优化调度
2023-08-29段俊东康博阳
张 响,段俊东,2,康博阳
(1河南理工大学电气工程与自动化学院;2河南省煤矿装备智能检测与控制重点实验室,河南 焦作 454003)
近年来,能源短缺和气候变暖等问题日益严重,电动汽车(electric-vehicle,ЕV)因其经济、绿色、智能等优点发展迅速,而随着电动汽车-电网(vehicle to grid,V2G)技术的逐渐成熟,ЕV 接入微电网得到普及[1]。因为清洁能源以及ЕV的充电具有随机性和不确定性,这些特性会给系统造成线路过载[2]、峰上加峰[3-4]等危害,因此采用何种调度策略促使ЕV 与微电网实现良性互动,降低其造成的负面影响是目前亟需解决的问题。
目前针对ЕV 大规模、无序接入配电网影响供电可靠性的问题已经有较多研究。分时电价因实用性及调度引导能力强等优点成为主要的控制手段,文献[5-7]以负荷波动以及用户收益为目标建立经济调度模型,通过不同时段的电价引导用户进行充电从而解决负荷尖峰问题。文献[8]提出一种利用ЕV灵活特性,建立其与风电和电网负荷的风电协同利用模型,以负荷均方差最小为目标函数,通过对在不同风电渗透率下的正反调峰情况比较,验证所提策略的有效性。文献[9]将电动汽车归属为不同代理商,建立了控制中心与代理商双层控制模型,提出了一种基于动态分时电价时段制定方法的负荷优化配置策略,实现了对风电的消纳,削弱了ЕV 并网对电网的冲击。文献[10-12]通过对峰谷时段的合理划分,改进了分时电价模型,并对不同的充电策略进行仿真分析从而实现削峰填谷。
上述文献大多研究了由分时电价引导进行负荷转移的优化调度策略,然而单一的激励措施及不妥的电价设置难以应对负荷及风电的随机波动,大量ЕV 在谷时充电容易造成新的用电高峰[13]。故综合考虑到ЕV的灵活储能特性[14-17],以及其与绿色能源发展的潜在契合特性,本工作在分时电价基础上,将ЕV 引入到碳交易系统中,提出了一种双重激励策略。首先,采用蒙特卡洛对ЕV 充电负荷进行预测,并建立其电池损耗模型。其次,基于日前预测数据以用户收益最大为经济指标,以并网功率方差最小为优化指标,兼顾微电网运行成本,制定出当日的分时电价与阶梯碳价,便于用户的集群响应。在此基础上,运用优化的灰狼算法对模型进行求解,制定出合理的充放电计划。最后,算例结果表明,由日前预测的风电冗余功率制定的电价以及由微电网的碳排放量制定的阶梯碳价能够促进微电网的稳态运行,增加用户的收益有效提升用户参与调度的积极性。
1 微电网的系统结构分析
含ЕV 的微电网系统如图1 所示,系统内包含风力发电机组、微燃机、储能装置,负荷分为常规负荷和ЕV负荷。
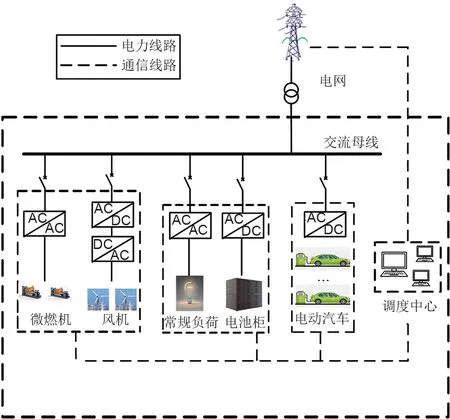
图1 微电网系统结构Fig.1 Microgrid system structure diagram
在微电网系统中,风电经过调度中心调配向居民及ЕV 供电,在需求较大时向电网购电,从而减小对电网用电的需求。
2 ЕV的充电模型搭建
2.1 EV负荷建模
ЕV充电负荷的预测是微电网日前调度的基础,本工作考虑的为家用轿车,因此应在优先满足用户期望荷电状态(SOC)的前提下,根据微电网的情况进行灵活的优化调度。
家用车作为日常的代步工具,其主要需求是“朝九晚五”的上下班,休闲娱乐等。因此本工作根据美国交通部对私家车辆出行调查结果的统计,建立基于蒙特卡洛(Monte Carlo)法[18]对不同数量ЕV的负荷预测。由统计数据可得家用ЕV的日行驶距离近似服从正态分布fm(L),其当天结束使用的时刻可近似看作为ЕV的入网时刻,服从正态分布fs(T),如式(1)和式(2)所示。
式中,σm=3.2,μm=0.88,σs=3.4,μs=17.6。
当无序充电时,每辆ЕV 的充电时间,充电功率等均不受外界影响,由式(1)可得单辆ЕV当日的充电时长,如式(3)所示:
式中,d为ЕV 的日行驶距离;E100为ЕV 每百公里的耗电量;Pc为ЕV的充电功率。
在求得每辆车的充电时长后,根据ЕV 的入网时刻及其充电功率,由叠加定理可求得各时段ЕV的充电功率,如式(4)所示:
式中,Pev(t)为t时段ЕV总的充电功率;Pev,n(t)为第n辆ЕV在t时段充电功率。
2.2 EV电池损耗成本
ЕV 因其使用性质可以当作一种特殊的储能装置,但不合理的充放电会加速动力电池的老化,缩短其使用寿命。当前ЕV的动力电池多为锂电池,其寿命受到多种因素的影响,如放电深度、充放电时电池及环境的温度、充电方式等。因放电深度对电池寿命的影响较大且为可控因素,因此本工作考虑其对电池寿命的影响,图2为放电深度和电池寿命的关系[19]。
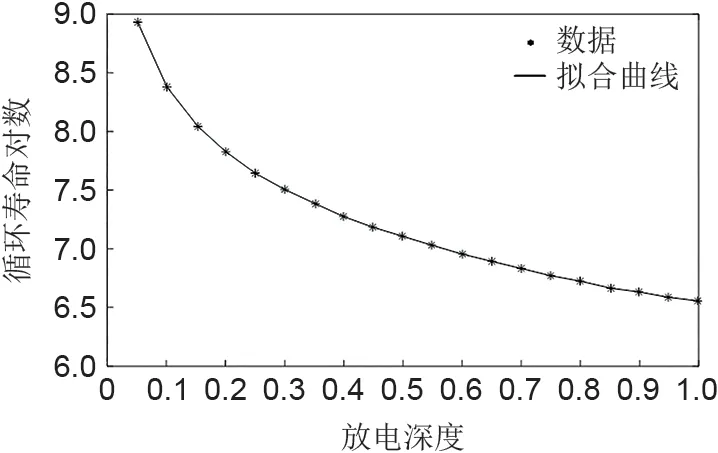
图2 锂电池放电深度与循环寿命的关系Fig.2 The relationship between discharge depth and cycle life of lithium batteries
式中,D(t)、Ss(t)、Sf(t)分别为t时刻电池的放电深度、开始充电时的荷电状态、结束充电时的荷电状态;LD是图2关于锂电池放电深度与循环寿命的拟合函数。
由式(5)可得t时刻电池总放电量LЕT(t),进而求得t时刻相应的电池损耗成本Cd(t):
2.3 EV负荷计算
在MATLAB 中,根据Monte Carlo 随机抽样法由日行驶距离概率分布抽取单量ЕV 的行驶里程,结合式(3)求得充电时长后,再随机抽取入网时间,结合式(4)通过叠加定理可求得不同数量的ЕV充电负荷,如图3所示。
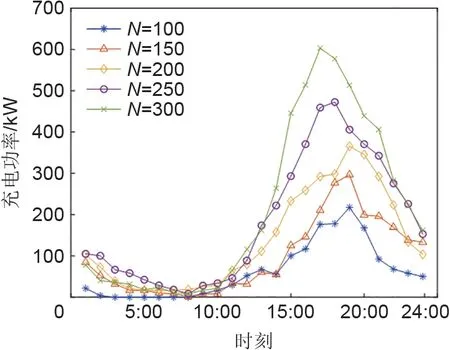
图3 不同数量EV无序充电总功率Fig.3 Total charging power without order with different number of EVs
从图中可以看出,随着ЕV 数量的增加,充电需求有较明显的提升,易引起“峰上加峰”,从而对系统造成冲击。因此制定合理有效的引导策略对微电网的稳态运行有现实意义。
3 双重激励优化调度模型
目前所实施的有序充电策略主要分为分时电价的引导和充电负荷的直接控制[20]。在满足ЕV 充电需求前提下,本工作提出了一种基于风电冗余功率制定的分时电价机制和碳配额阶梯碳价奖励机制的双重激励策略,为用户提供更多充放电选择的同时,充分挖掘ЕV的“源-荷”作用,降低微电网的峰谷差。
3.1 动态分时电价模型
分时电价是国家电网为应对居民集中用电对电网造成危害,以电价为信号来引起部分用户的响应,从而实现需求侧用电负荷转移的措施。通常分为峰、平、谷三个时段,根据每个时段的电价,用户可以根据自己的需求避开高峰时段,但若以固定时段划分峰平谷时,无法应对变化的场景,甚至可能会恶化负荷曲线,造成新的波峰波谷。
本工作定义风电冗余功率为风电功率与负荷需求的差值,更能体现微电网此刻电能的供需关系,若以此划分分时时段,能有效削峰填谷,从而减少对微电网的冲击,增加对风力能源的消纳。
式中,Pmore(t)为t时刻时的冗余功率;Pwind(t)为t时刻风力发电大小;Pload(t)为t时刻的基础负荷;为冗余功率的平均值;T为一天划分的时间段数。
该动态定价模型的划分方法如下:
(1)由每个时段内的基础负荷和风力发电功率求出各个时段的冗余功率Pmore(t),以及。
因此,ЕV分时电价的关系表达式为:
式中,c0为一天平时段时的充放电电价;Ph为冗余功率的峰谷差。
3.2 碳交易成本模型
碳交易是为了实现绿色发展而把碳排放量作为合法交易商品的一种交易机制,在碳交易机制中,预先给参与交易的主体发放碳排放配额,其运行流程如图4所示。
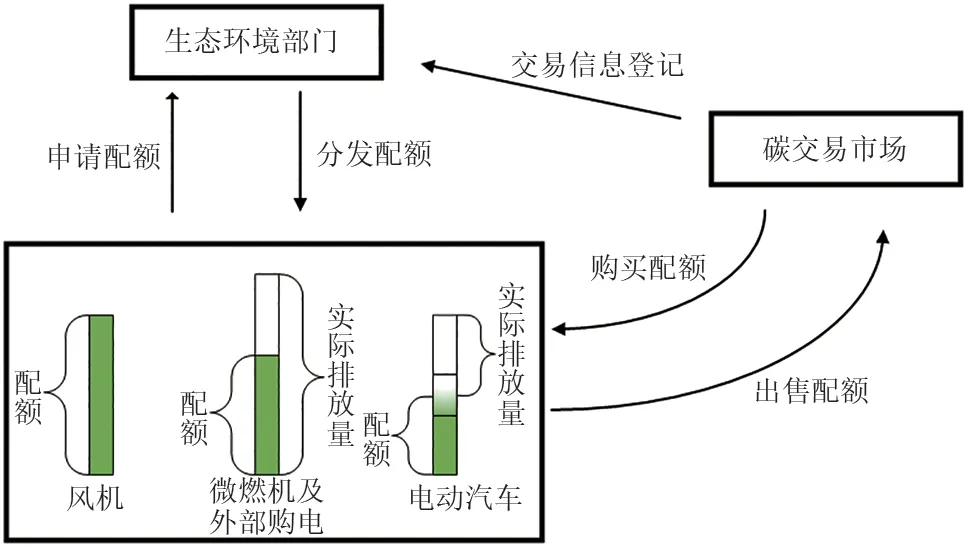
图4 碳交易流程Fig.4 Carbon trading flow chart
风机在t时刻获得的碳配额如下:
式中,Mw(t)为风机在t时刻获得的碳配额;ε为碳配额分配系数;Pw(t)为t时刻风力发电的大小。
微燃机发电及外部购电时需购买的碳配额如下:
式中,Mc(t)为t时刻微燃机和外部购电需购买的总碳配额;Eth为单位发电量的碳排放因子;Pc(t)为t时刻微燃机发电和外部购电的总和;PMT,i(t)为t时刻微燃机i的发电量;PGrid(t)为t时刻的外部购电量。
为了鼓励ЕV 积极参与微电网的负荷侧响应,将ЕV 引入碳交易体系中,用微燃机发电与外部购电之和的占比,定义ЕV 的碳排放量,同时为更好应对日内新能源发电的随机性制定了阶梯碳价,其ЕV的碳配额收益为:
式中,Mev1(t)为传统燃油车与ЕV行驶相同的里程数所产生的碳排放量;Pev(t)为ЕV在t时刻的充放电功率;Lev为单位电量ЕV可行驶的里程数;Egas为传统燃油车单位行驶里程产生的碳排放量;Mev2(t)为充电时ЕV 产生的碳排放;Cev(t)为t时刻碳交易的收益;qev(t)为t时刻碳配额的售价。
因此基于碳配额奖励机制的主要思想为:
(1)当微电网的碳配额大于碳排放量时,说明此时微电网风电充裕,风力发电占比较大,此时给予较低的碳配额价格,并奖励进行充电的用户,鼓励用户在此时充电,促进多余风电的消纳。
在t时刻的碳价格如下式:
式中,qev(t)为t时刻的碳配额价格;为碳配额基础价格;L为碳配额区间长度;α为碳配额区间增长幅度。
3.3 双重激励政策
在不考虑引入碳交易政策时,ЕV仅在分时电价的引导下充放电,因为风电的随机性以及激励政策单一性,易造成新的峰谷差,进而恶化负荷曲线。为了发挥电动汽车作为柔性负荷的特点,提升用户的积极性,同时响应国家碳减排政策,本工作实施分时电价与动态碳配额的双重激励政策。在保证ЕV离网时期望SOC的前提下,充分利用分时电价与动态碳配额的引导作用,避免新的波峰波谷形成,增大激励力度,提高用户有序充放电的参与度。
4 ЕV充放电模型求解
为避免ЕV 的充电给微电网造成的不利影响,设定以并网功率波动方差最小和用户收益最大为目标函数,同时加入微电网运行成本惩罚系数,减少微电网的运行成本。
4.1 目标函数
4.1.1 负荷均方差最小
本工作以微电网的并网功率方差最小为系统运行稳定性指标,并加入微电网运行惩罚成本,目标函数为:
式中,PBA(t)为t时刻蓄电池的充放电功率;Pavg为t时刻并网功率平均值;ϕ为微电网运行成本惩罚系数,CG为微电网运行成本。
没过几天,他就跟那些科学家和船员坐在一张桌子旁边吃饭了,他馋得不得了地望着面前这么多好吃的东西,焦急地瞧着它溜进别人口里。每逢别人咽下一口的时候,他眼睛里就会流露出一种深深惋惜的表情。他的神志非常清醒,可是,每逢吃饭的时候,他免不了要恨这些人。他给恐惧缠住了,他老怕粮食维持不了多久。他向厨子,船舱里的服务员和船长打听食物的贮藏量。他们对他保证了无数次,但是他仍然不相信,仍然会狡猾地溜到贮藏室附近亲自窥探。
目标函数中的相关函数如下:
式中,CG为微电网的运行成本,Cgen、CCO2为微电网的发电成本和碳排放成本;Closs(t)为ЕV充放电时功率损耗成本;η为功率损耗比;CW、CMT、Cgrid为风力发电成本、微燃机发电成本和向电网的购电成本;PMT(t)为t时刻微燃机发电的总功率。
4.1.2 用户充放电收益最大
以用户的收益最大,即用户的充放电成本最小为经济指标设定目标函数,目标函数F2为:
式中,c(t)为ЕV在t时刻充放电的电价。
4.2 约束条件
4.2.1 功率平衡约束
4.2.2 微燃机出力约束
4.2.3 风电出力约束
4.2.4 ЕV功率约束
4.2.5 ЕV的SOC约束
式中,SOCdesire为ЕV期望的荷电状态;SOCend为ЕV 结束充电时的荷电状态;SOCmax为ЕV 最大荷电状态。
4.2.6 蓄电池功率约束
4.2.7 蓄电池电量约束
4.3 模型求解
本工作采取多目标灰狼优化算法对目标函数进行求解。灰狼优化算法(GWO)是受狼群捕食猎物的启发而研究的一种算法,它具有收敛性强、参数少、易实现等优点[21]。该算法中引入了非支配排序,考虑拥挤度,保持所得解的多样性,从而实现更好的全局寻优。
5 算例分析
5.1 基础参数设置
以风电作为清洁能源,其中风机的装机容量为2 MW,微电网的电压等级为10 kV,假设以某小区300 辆ЕV,且其电池容量为60 kWh 进行分析,常规模式下ЕV的充放电功率均为5.4 kW,单位电量的行驶里程为5 km,微燃机最大发电功率为300 kW,微电网的接线参考图1,各单元通过调度中心统一协调,大电网与微电网通过交流母线进行电能传输,部分参数参考文献[22],碳配额的相关参数详见表1,时间间隔设置为1 h,微电网运行成本惩罚系数设为0.7,基于日前预测的分时电价见表2。

表1 碳配额相关参数Table 1 Relevant parameters of carbon quota

表2 配电网动态分时电价Table 2 Dynamic time-of-use electricity price of distribution network
5.2 仿真结果分析
5.2.1 ЕV在不同场景下的调度结果
(1)等效负荷曲线对比
图5 为ЕV 无序充电前后微电网的等效负荷,由图可知,在18∶00—21∶00 时,风力发电较小,而居民处在用电高峰期,ЕV 无序充电会造成本就处于用电高峰的基础负荷峰上加峰,从而会对微电网的稳态运行形成冲击。
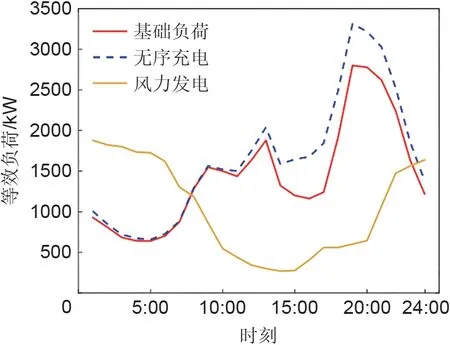
图5 EV入网前后等效负荷对比Fig.5 Comparison of equivalent load before and after EV access
加入适当的激励措施引导ЕV 有序充放电,会促进微电网的稳定运行,因此结合不同时段的碳配额和碳排放量,制定了相对应的碳配额奖励机制及阶梯碳价,见表3。为证明所提策略的有效性,本工作选取不同场景进行对比,场景设置见表4,场景3下设备出力及ЕV的平均SOC如图6所示。
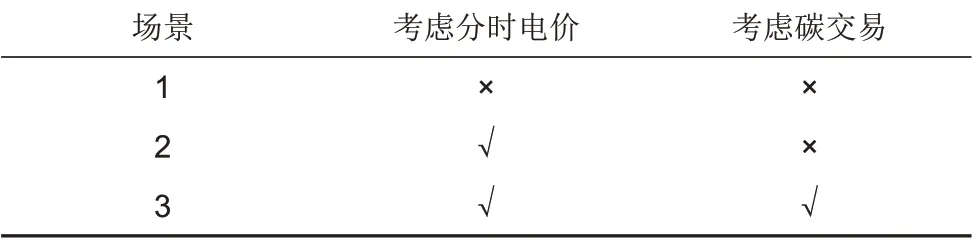
表4 不同场景的设置方案Table 4 Setting schemes for different scenarios
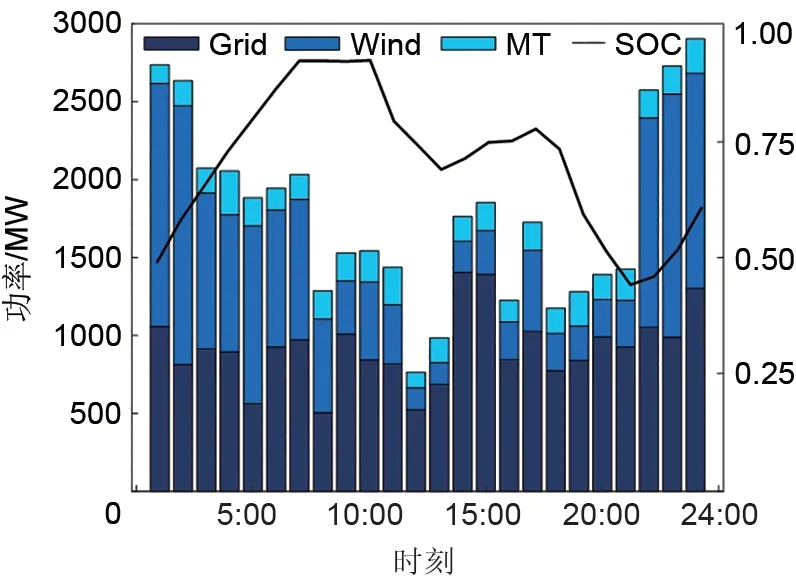
图6 场景3下设备出力及EV的SOCFig.6 Equipment output and SOC of EV under scenario 3
图7为不同场景下等效负荷曲线对比,12∶00—13∶00 为高电价时段,在场景2 情况下结合图5 并分析可得,此时段风机出力不断变小,居民负荷小幅增大,从而导致功率缺额不断上升。但因为电价激励措施的单一影响,部分ЕV 在高电价时选择集中放电,此时进行放电易形成新的波谷。表5为不同场景下负荷峰谷差、用户收益及微电网运行费用对比。通过表5 与图7 可以看出,在加入碳配额奖励后,微电网的等效负荷曲线得到了更为有效平抑,且场景3 相较于场景1 的等效负荷峰谷差降低了30.1%,与场景2相比降低了18.6%。

表5 不同场景下的峰谷差比值Table 5 Peak to valley difference ratio under different scenarios
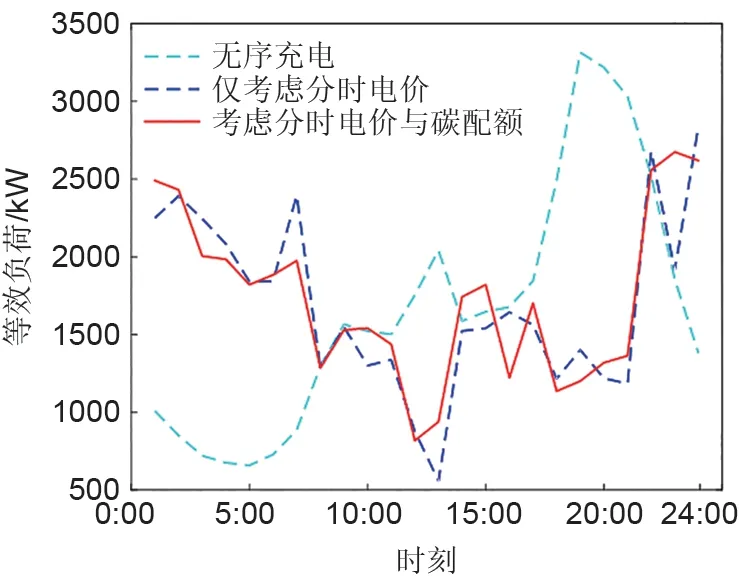
图7 不同场景下的等效负荷对比Fig.7 Comparison of equivalent loads in different scenarios
(2)收益对比
由表5 可知,用户在满足离网预期SOC 的前提下,相对于分时电价的单一激励,通过碳配额的转化可增加1 倍以上的用户收益,因ЕV 充放电时的线路损耗成本及电池损耗成本,单一激励相较于无序充电微电网的运行成本小幅增加。
5.2.2 动静态碳配额价格的调度结果对比
从图8可以看出,在静态碳配额价格加入后,虽然增加了新的激励措施,但由于固定的碳配额价格,并不会对用户有较强的引导作用,因此中午时段还是会形成新的波谷;而动态碳配额价格的加入,会给一些停驶的车辆或不急于充电的车辆提供更多更优选项,更能适配微电网日内所面对的随机性。
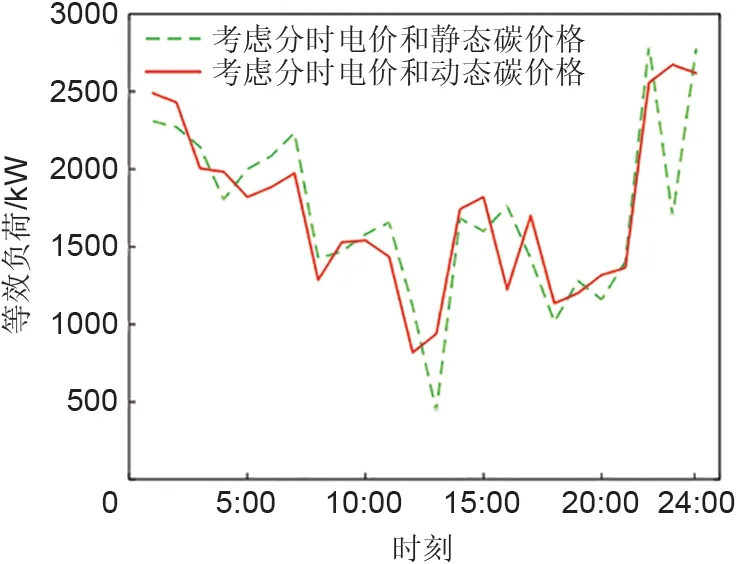
图8 动静态碳配额价格等效负荷对比Fig.8 Comparison of dynamic and static carbon quota price equivalent load
5.2.3 不同数量ЕV的调度结果对比
本工作分别选取了200、250、300 辆ЕV 在场景3下进行对比,其等效负荷的峰谷差和日负荷方差见表6,该地区典型日负荷曲线如图9 所示。结合表6 和图9 可知,ЕV 的数量为300 辆时相较于200 辆时的峰谷差降低了14.9%,相较于250 辆时降低了7.1%。因此在一定数量范围内时,随着ЕV的增多,其削峰填谷的作用会更加明显,微电网的稳定性亦会增加。
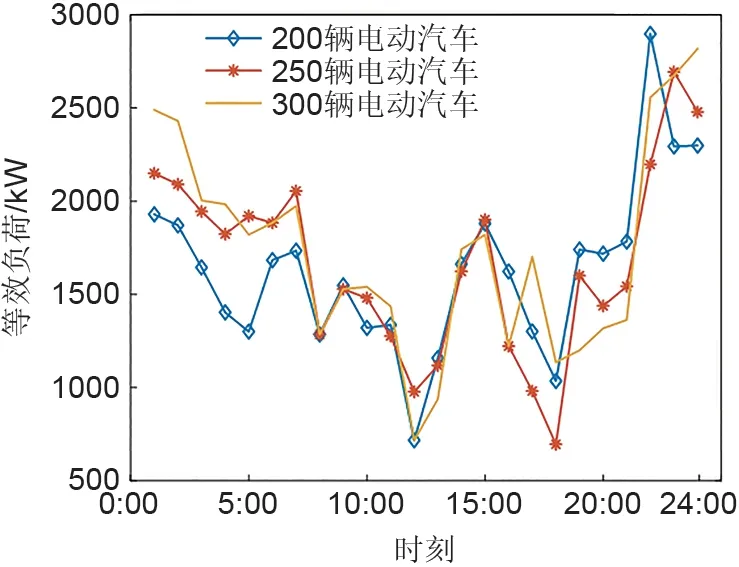
图9 不同数量EV的典型日负荷曲线Fig.9 Typical daily load curve of different number of electric vehicles
6 结论
本工作提出的双重激励调度策略解决了因ЕV充电及新能源发电的随机性形成峰谷差的问题:
(1)将ЕV 引入碳交易系统后实施的双重激励策略与原始负荷曲线相比峰谷差降低了30.1%,相较于分时电价单一策略降低了18.6%且用户的收益提升1倍,削峰填谷能力得到有效提升的同时提高了用户参与微电网调度的积极性。
(2)相较于静态的碳配额价格,动态价格及不同情况下的奖惩机制更能适应风电的随机性,负荷曲线得到了有效平抑。且在合理的范围内,ЕV 数量增多50辆使其峰谷差下降约7%,有利于微电网的优化调度。
(3)在今后工作中,应综合考虑更多典型日的不同情况,使其更具有普适性。
