“正方体截面的探究”教学设计

李新国 _ 北京市铁路第二中学

案例分享

教学目标

结合正方体截面设计的一系列问题，引导学生完成探究、发现、证明新问题的过程，积累数学探究的经验。

教学情境

用一个平面截正方体，思考截面的形状将会是什么样的。学生自主或在教师引导下提出问题，解决问题，培养深刻思考的能力。

教学过程

1.知识准备

复习相关概念：截面、截面的边、平面与平面平行的性质定理、等角定理等。

问题：用一个平面去截一个正方体，会得到什么形状的截面图形？

分析：如果构成多边形，平面与正方体最少有3条交线，最多有6条交线，所以，截面图形可以是三角形、四边形、五边形和六边形。

设计意图：为后面逻辑推理作铺垫。

2.教学过程

【探究1】若截面图形是三角形，可以截出几类不同的三角形？为什么？

分析：如图1所示，可以是等边三角形，也可以是非等边的等腰三角形，不可以是直角三角形和钝角三角形。直角三角形不成立的证明，可以使用反证法，利用线面垂直推导出矛盾，也可以使用余弦定理证明截面三角形只能是锐角三角形。

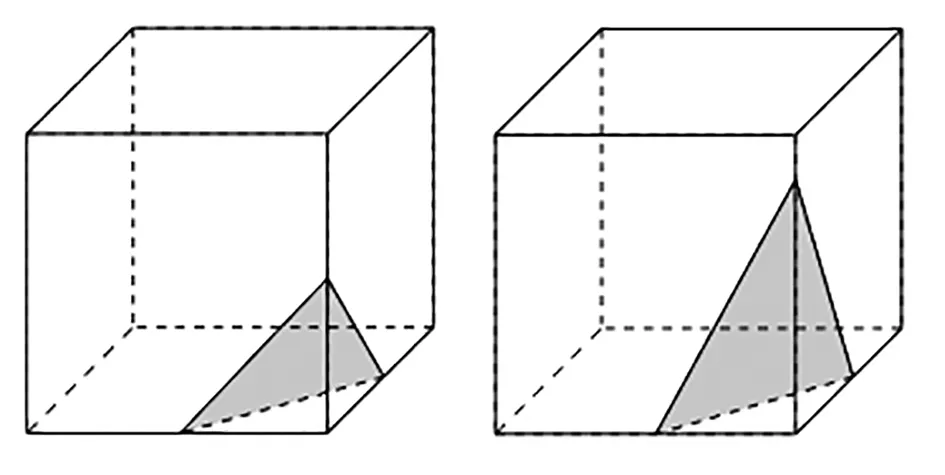
图1

【探究2】

问题1：截面图形是否可以是平行四边形？若成立，可以截出几类不同的平行四边形？

分析：如图2所示，可以截出正方形、矩形、菱形和一般的平行四边形。

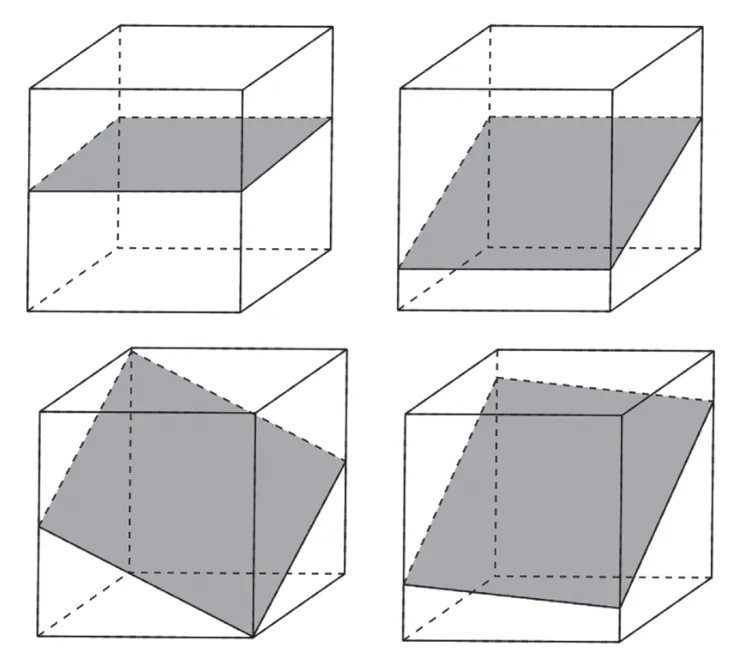
图2

问题2：截面图形是否可以是梯形？若成立，可以截出几类不同的的梯形？

分析：截面图形可以是一般的梯形，可以是等腰梯形（如图3所示），但不能是直角梯形，证明方法类似截面不能是直角三角形。

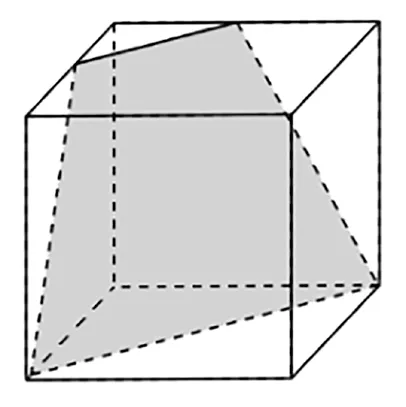
图3

问题3：截面图形是否可以是一般的四边形？

分析：不可以，由于正方体六个面中，上下、左右、前后两个面互相平行，若一个平面与四个面相交，至少与其中一对平行平面相交，则至少有一组对边平行，所以只能得到梯形和平行四边形。

设计意图：先从简单的四边形入手，从易到难，从特殊到一般，学生容易理解，然后再理性思考截面四边形为什么一定是平行四边形和梯形。

【探究3】若截面图形是五边形，则五边形的边、角之间有什么特征？

分析：若截面图形是五边形，需要和正方体的五个面相交，其中一定和上下、左右、前后中的两对平行，平面相交，所以，得到的五边形有两组对边平行，根据等角定理得到两个角相等（如图4所示），不能是正五边形。

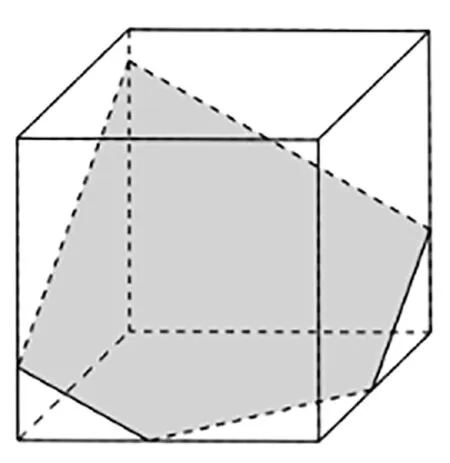
图4

【探究4】若截面图形是六边形，则六边形的边、角之间有什么特征？

分析：类比探究3可知，截面六边形有三组对边平行，三对角相等，可以是正六边形（如图5所示）。

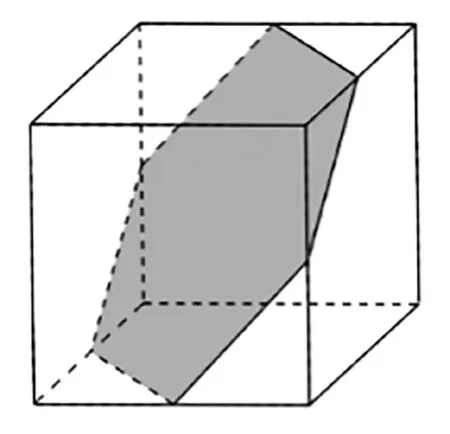
图5

设计意图：由于有截面是四边形的研究过程作铺垫，比较容易过渡到五边形和六边形截面问题，引导学生利用两个平面的交线准确作图，画出五边形和六边形。

3.拓展探究

【探究5】若与正方体对角线垂直的平面截正方体，截面面积最大的图形是什么图形？为什么？

设计意图：截面面积最大的图形是类似图5的正六边形。探究5是一个综合性较强的问题，若学生认知水平比较高，可以在前4个探究问题的基础上进一步深入；若学生接受起来比较困难，可以将该问题放置在以后的教学中再进行探究。

教学反思

1.教学中要帮助学生建立直观想象

可以利用几何画板、玲珑3D几何、GeoGebra等软件，做好动态演示的课件，作为辅助学生理解的材料，让学生通过信息技术软件进一步直观理解正方体的截面形状。

2.要由直观想象过渡到逻辑推理

观察不能代替严格的数学证明，探究的难点是分类找出所有可能的截面，并证明哪些形状的截面一定存在或一定不存在，此时需要用学过的数学理论知识进行证明。在研究中，鼓励学生通过操作观察形成猜想，然后给出证明结论，完成从感性认知到理性思考的过程，对前面所学的空间中平行和垂直关系的判定和性质有进一步认识。

3.问题的设置要循序渐进、因材施教

在教学前要复习回顾之前学过的知识，在探究的过程中遵循先易后难、由特殊到一般的顺序。正方体的截面问题可以引申出很多问题，这是一个跨度很大的系列问题，在教学过程中，要针对学生的情况选择适合学生认知水平的内容。

闻岩老师点评

高中数学必修部分立体几何内容的学习，重点是对空间图形性质的研究，通过直观感知、操作确认、推理论证、度量计算，可以实现由表及里、从定性到定量的认识，使学生逐步建立空间观念。其中，作图是立体几何学习中培养直观想象素养的重要契机。立体几何教学要求学生“认真读题，根据题意先作出直观图”，并且要把图画得尽量准确，以利于看出，进而理性分析、论证各种关系。这节课的教学设计借助解决正方体截面问题，开展问题探究活动，学生可以直接进行抽象研究，也可以借助技术演示进行直观观察、理性分析，但都需要学生认真作图，完成“在研究问题的过程中，要给出合理的作图；并结合几何图形，对结论给出合理解释”的任务。

本节课研究的内容不是一个题的解法，而是对一个“数学问题”的研究，这在数学教学中意义重大。立体几何往往要研究某一类几何图形的结构特征，一般情况下，要通过对具体实例的组成元素及其相互关系的观察、分析，归纳出共性，再概括到一般，形成一类几何图形的定义，在此基础上给出“三种语言”进行表示，并从“特殊的组成元素”“特殊的位置关系”入手，对这类几何图形进行更细致的分类。本节课中正方体截面的研究过程就体现了立体几何中数学问题的一般性的研究规律。

本节课的教学内容也非常适合改写成学习资源，供学生在单元学习时使用。