浅谈门座式起重机变幅机构运动规律

马明楠

（江南造船（集团）有限责任公司，上海 201913）

门座式起重机是船舶造修企业的主要起重设备，其运行正常与否，直接关系到船舶修造的进程及生产任务的完成。为了保证门座式起重机的安全运行，在每台起重机上都安装有力矩限制器，用以指示当前起吊的重量、工作幅度。当起吊重量和工作幅度超出了允许的力矩范围，力矩限制器就会发出控制指令，限制起重机的工作，保证起重机的安全。

如果起重机力矩限制器的幅度指示发生故障，显示错误的幅度值，就会影响正常的生产。当显示幅度值大于实际值时，就会限制起重机的起吊能力，在实际可以起吊的情况下，由于显示幅度值的偏差而不能起吊。当显示幅度值小于实际值，力矩限制器会允许起吊较大的重量，从而引发起重机的超载，直接影响安全生产。

对此，需对每台门座式起重机制作用于指示起重机实际工作幅度的机械式幅度指示器。机械式幅度指示器由指针和表盘组成，安装在起重机臂架上。表盘与臂架固定，跟随臂架的转动；指针的一端用转轴与臂架相连接，另一端（指针尖端）靠自重保持向下的状态；当臂架摆动到某个幅度时，表盘也跟随臂架转动到某个位置，此时，指针即指示出起重机的实际幅度值。

制作机械式幅度指示器，关键是绘制幅度指示器的表盘刻度。为了绘制表盘刻度，需要获得臂架角度与起重机工作幅度的对应关系，即臂架角度与工作幅度的对照表。通常，对照表采用现场取值的方法获得。即把指针安装于臂架上，然后，根据地面实测幅度值，在刻度盘上做上刻度记录。这种方法不但需要花费很长的时间进行取值，而且由于读取、记录、制作等多重环节的误差积累，最终结果误差较大。另外，由于这种方法需要现场作业，将占用大量起重机工作时间，在生产繁忙的现在，如果每台起重机都采用这样的方法，必将严重影响生产。因此，我们提出采用较为简单的方法—运用数学几何计算的方法来获取对照表，即利用几何原理建立门座式起重机臂架角度与起重机工作幅度之间的函数关系，并通过设定不同的臂架角度，求算对应的幅度值。

现有的门座式起重机中，起重机的臂架系统主要有2 种结构形式：（1）单臂架结构；（2）四连杆结构。单臂架的结构形式较为简单，其幅度与臂架角度之间存有简单的余弦关系，因此，建立单臂架门座式起重机的幅度和臂架角度数学关系式也就比较简单（见图1）。而四连杆结构的门座式起重机，其臂架夹角与幅度的关系较为复杂，需要通过几何分析等数学方法加以推导。

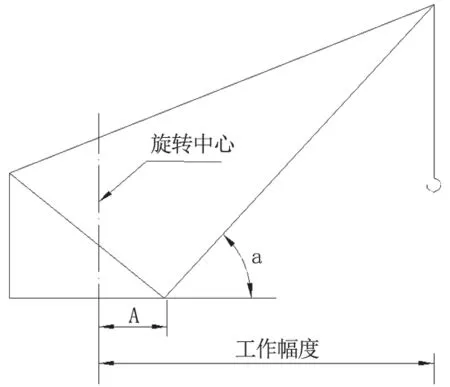
图1 单臂架门座式起重机臂架结构

首先，我们来看一下四连杆机构的结构图（如图2），O 点为臂架下铰点，A 点为人字架上铰点。OC 为臂架、AB 为大拉杆、BCD 为象鼻梁。

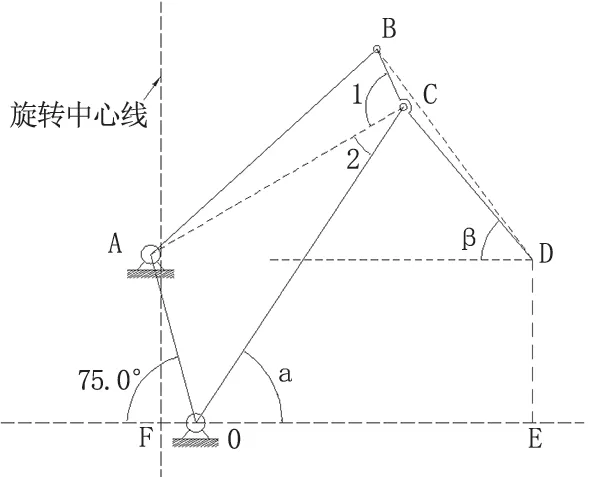
图2 120T 变幅四连杆结构图

由图可知，杆OA 是起重机机架，为不动件，杆OC是起重机的臂架，为主动件，随着OC 的运动，即臂架角度（∠COE）的变化，象鼻梁BCD 做相对运动，起重机的工作幅度（FE）亦随之变化。本文以某公司120T门座式起重机为例来求算臂架角度α（∠COE）与幅度FE 之间的关系。

根据120T 门座式起重机的图纸，我们可以获知，∠AOE=105°，OA=15.013m，OC=32.538m，AB=26.307m，BC=5.498m，CD=17.19m，BD=22.532m，OF=3m。

在图2 中添加辅助线连接AC 两点，并设∠ACB=∠1，∠ACO=∠2，过D 点做OE 的平行线，设其与CD的夹角为β。

根据三角余弦定理，在△AOC 中有

同理，在△ACB 和△ACO 中可写出：

由此可得：

在图3 中， 延长BC 和DH 相交于G， 并设∠GCD=∠4，∠CGH=∠5。

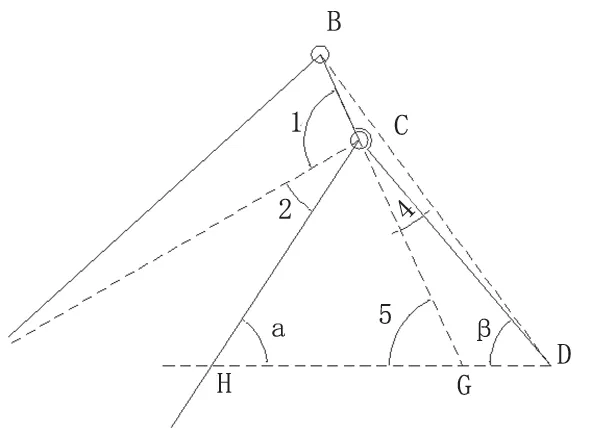
图3

由△BCD，可得

式中，BC、CD、BD 为已知，代入上式后可得

由图3 可知：

由图1 可知

由式（1）～（6）可立方程式

此方程组即为起重机臂架角度α 与起重机工作幅度FE 之间的数学关系。

数学关系是建立以后，如何求解也是一个问题。如果采用常规的计算方法，对每个臂架角度都一步一步地进行计算，将耗费很长的时间，并且容易产生计算错误。因此，我们利用Microsoft Excel 的函数计算功能，把各个已知量输入表格，并在相应的表格中建立函数关系式，利用Excel 帮助计算。图4 是输入已知量后的状况。

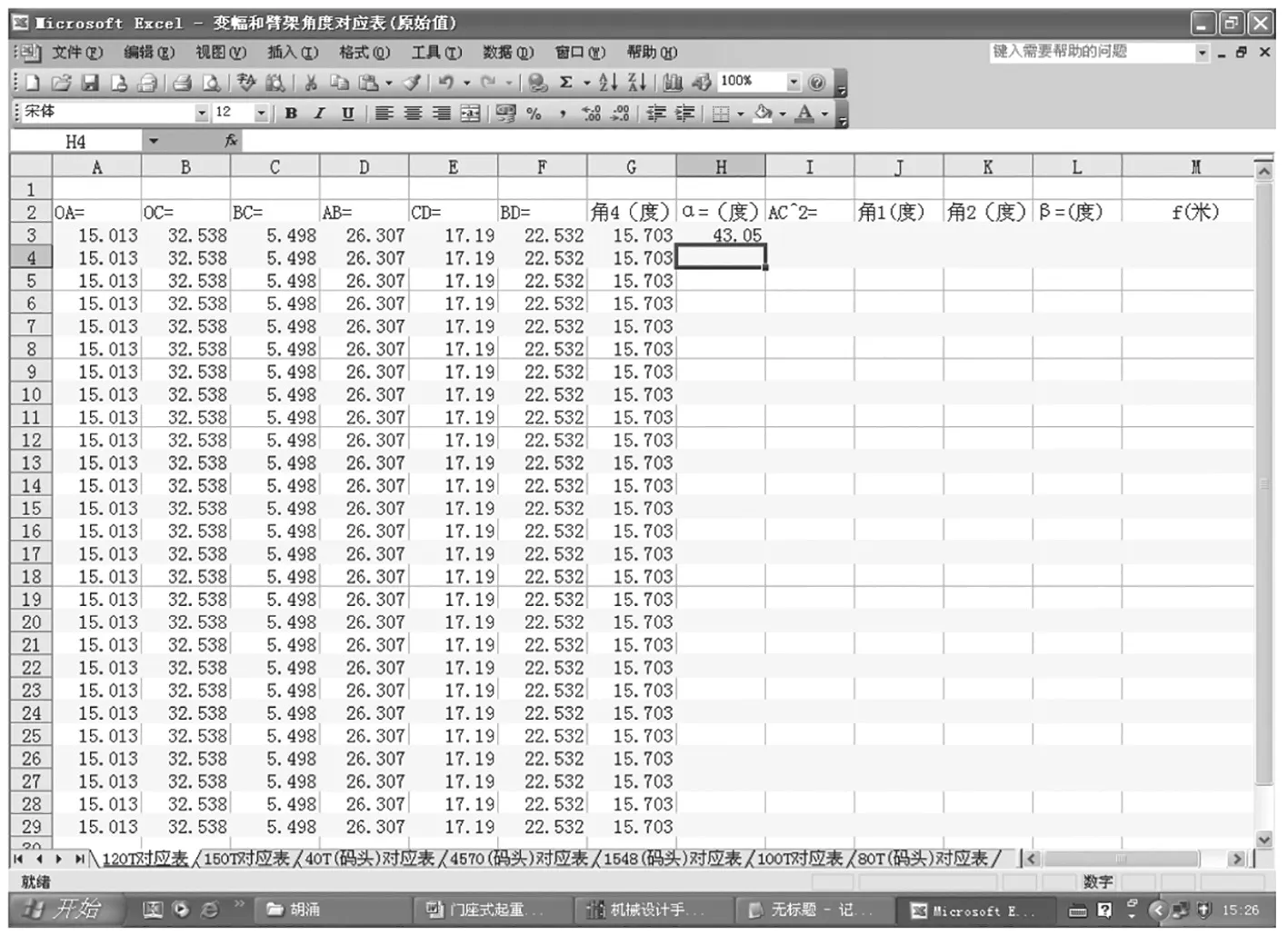
图4

然后在第3 行的其他对应表格中根据方程组建立未知量与已知量间关系。

在AC2下面的I3 格中输入以下方程：

= P O W E R ( A 3 , 2 ) + P O W E R ( B 3 , 2 ) -2*A3*B3*COS(105*PI()/180-H3*PI()/180)。

在角1 下面的J3 格中输入：

=A C O S((I 3+P O W E R(C 3,2)-P O W E R(D 3,2))/(2*SQRT(I3)*C3))/3.1415926*180。

在角2 下面的K3 格中输入：

=A C O S((I 3+P O W E R(B 3,2)-P O W E R(A 3,2))/(2*SQRT(I3)*B3))/3.1415926*180。

在β 下面的L3 格中输入：=J3+K3-H3-G3。

最后在f（即FE）下面的M3 格中输入：=B3*COS(H 3*PI()/180)+E3*COS(L3*PI()/180)+3

Excel 自动帮助我们计算出各个未知量。如图5 所示。

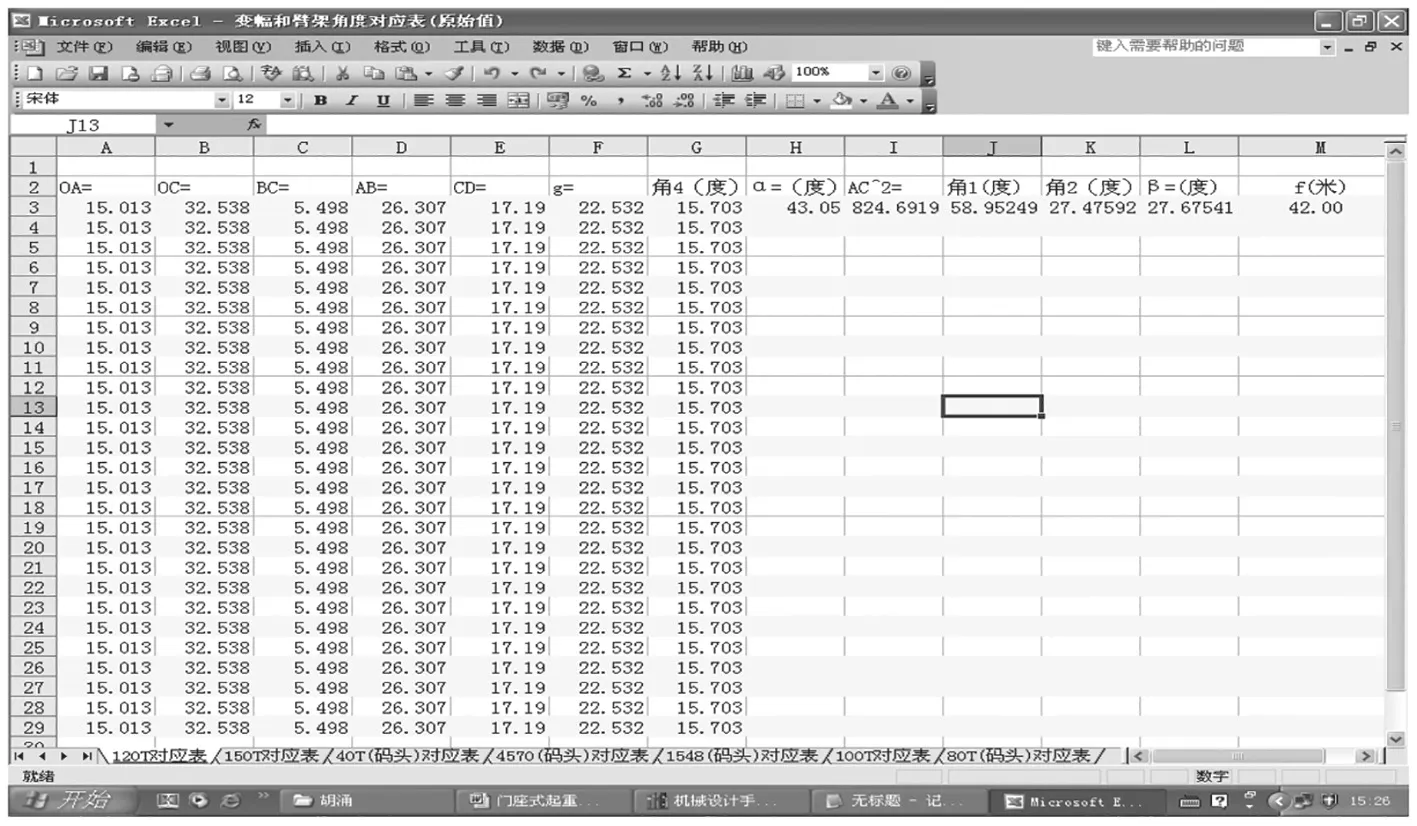
图5

利用Excel 的拖放复制功能，可以很容易地将输入的计算公式复制到下面的行列中。

在Excel 表格的H 列中，我们根据变幅的角度范围（40°～70°），在变幅范围内以每一增量为0.01°输入不同的臂架角度α 值，即可获得在对应角度下各个相关参数的值（中间计算值），以及我们所需要的变幅幅度值（f）。

为了验证计算结果的正确性，我们选择几个臂架角度，在AUTOCAD 中绘出臂架系统并测量幅度FE 的值，结果和Excel 中的计算结果一致。同时，为保证理论计算值和实际状态下数值的一致性，我们通过对一台门机的几组数据进行现场实测，证实理论数据和实际数据间的差值，在误差范围以内。

通过Excel 的计算，我们得到许多不同α 值下的幅度值，并根据实际位置需要进行了筛选，表1 如下。

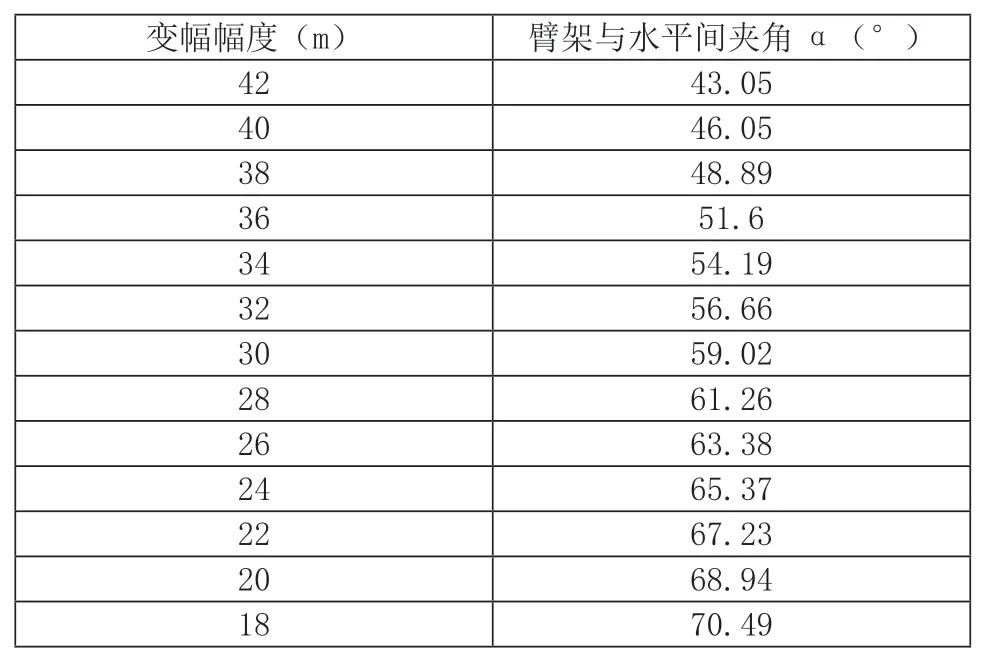
表1

最后，根据表1 在CAD 中绘制刻度盘的样式，为表盘的制作做好模板。

通过上述推导，我们不仅完成了工作，同时获得了四连杆结构的运动方程式，提高了工作的效率。我们运用此方程式不仅完成了120T 门座式起重机幅度值的计算，同时也很快完成了其他多台门座式起重机的幅度值的计算。通过计算机计算，我们可以把误差控制在较小的范围内，并且不占用起重机的工作时间，不影响起重机的正常生产活动。