江苏苏州碳排放演化特征及影响因素分析

叶晓岚 刘坤 庄斯宇

摘 要：本文以江苏苏州为研究对象，据不同能源的排放系数核算苏州能源消费的碳排放，通过对数平均迪氏指数法分解模型（Logarithmic Mean Divisia Index， LMDI）对苏州2011—2021年碳排放量及其影响因素进行分析研究。结果显示：经济建设发展是促进苏州碳排放增长的主要因素，效率因素对苏州碳排放彰显遏制作用，能源结构因素对碳排放的抑制作用与日俱增，工业结构因素对苏州碳排放影响效果不显著。因此，优化经济增长方式，实现经济增长与碳排放的脱钩；通过技术进步，实现能源强度的降低；推进结构性变革，实现能源消费和产业结构的低碳化是实现苏州碳减排的主要方式和重要路径。

关键词：碳排放因素分解；能源强度；能源结构；LMDI；苏州

本文索引：叶晓岚，刘坤，庄斯宇.<变量 2>[J].中国商论，2023（16）：-164.

中图分类号：F124.5 文献标识码：A 文章编号：2096-0298（2023）08（b）--04

2020年9月，我国明确提出2030年“碳达峰”与2060年“碳中和”目标。苏州作为我国内地最强地级市，在高能耗、环境负担重的现状下实现低碳转型面临巨大困境。为积极稳妥地推进“双碳”目标，苏州市政府制定印发《关于加快转变发展方式做好碳达峰碳中和工作的实施意见》，提出2030年前达到目标。

本文以苏州为研究对象，核算其在2011—2021年能源消费引起的碳排放，采用因素分解法分析苏州碳排放变动趋势及影响因素，探讨时间性差异，基于上述制订相关政策。

1 文献综述

如今，碳排放已成为国际学者与低碳减排学界的研究热题，影响碳排放的因素研究有分解与分析方法体系和回归分析方法体系两种。

一是分解与分析方法体系。通过构建碳排放恒等式，采用因素分解法分析影响碳排放的原因。其中，对数平均迪氏指数分解法（LMDI）是广泛使用的分解法，可在时空双维度展开分析研究，有效对各因素解析。从空间上来看，我国学者大多聚焦碳排放负载较大、经济较发达地区，如北京、上海等，通过能源消费数据对碳排放驱动因子进行分析。林晓洁等（2022）利用LMDI对香港地区能源消费演变趋势进行研究；姚永玲（2011）对北京市能源碳排放因素分解分析；孙燕燕（2020）对上海市旅游碳排放效應分解进行研究；杨燕、武戈（2013）基于南京市和苏州市比较分析，研究长三角城市工业碳排放因素分解模型。从时间上来看，孙冬营等（2023）利用LMDI方法探究城市生活用水量变化的驱动效应；纪义虎等（2022）通过LMDI因素分解法分析了沁河流域近20年碳排放增速变化趋势；宋辉等（2019）借助对数平均迪氏指数因素分解法，研究产业节能效应；张鸿武等（2016）从时间维度对工业碳减排技术效应进行研究；韩钰铃、刘益平（2018）基于LMDI探究在时间维度下区域碳排放中各驱动因子的贡献度。

二是回归分析方法。以计量经济学为基础，系统评估分析对象，其中IPAT和STIRPAT两大模型应用最为广泛。如龚利等（2018）基于STIRPAT模型的能源消耗影响因素研究；孙义等（2020）基于STIRPAT模型的辽宁省碳排放影响因素研究；彭芳（2023）基于IPAT模型对绿色建筑短期碳排放进行预测；王丽等（2017）基于IPAT模型的城市碳排放分析。

总之，关于碳排放影响分解因素的研究文献不在少数，从时间到空间、从局部到整体，研究文献极为丰富。基于LMDI因素分解模型的特征，不能同时对三个或更多结构性因素进行分析和考量，故为解决此缺点，本文使用二阶段LMDI因素分解法，一齐划分出包括效率因素（能源强度）、结构因素（能源结构，工业结构）、经济发展（人均GDP）多种影响因素对苏州碳排放的影响。

2 数据整理分析

2.1 碳排放核算方法

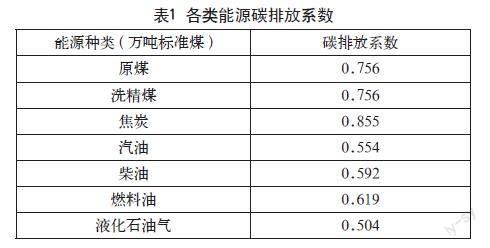
本文对苏州整体的碳排放量进行估算，参照徐国泉等（2021）基于各类能源碳排放系数的估算公式，公式如下：

其中，C表示碳排放总量；Fi表示第i类能源的碳排放系数（见表1）；Ei表示第i类能源消费量。能源种类不同，F值也不同。

2.2 数据来源

鉴于对比性强，通过实物量和《苏州统计年鉴2022》的能源折算系数，将苏州各类能源消费量换算为标准煤，其中数据来源于《苏州统计年鉴》2012—2022年。

2.3 苏州碳排放演化趋势

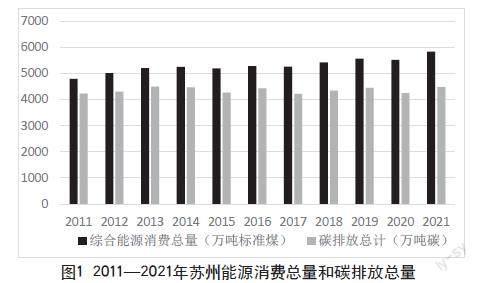
根据碳排放估算公式，可以得到苏州市2011—2021年能源消费的碳排放总量（见图1）。由图1可知，2011—2021年苏州市能源消费总量呈现逐年增长的趋势，且煤炭这种碳排放系数较高的能源仍然占据苏州总能源消费比重的首位。

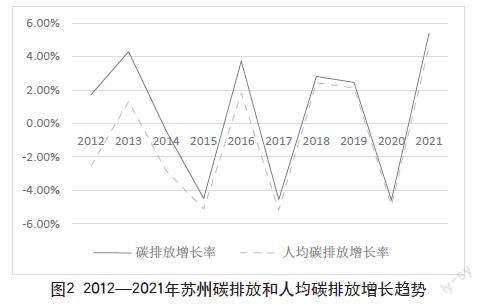
苏州碳排放总量及人均碳排放量增长率如图2所示，2012—2021年苏州有关能源消费的碳排放总量增长率大致呈现双“W”型，个别年份呈现负增长趋势，同时2021年达到增长峰值4478.8万吨。从人均碳排放总量增长率趋势来看，增长趋势大致为双“W”型，其中2018—2019年增长率趋于平缓，2021年同样达到增长峰值3.486吨煤每人。综上所述，苏州近十年的碳排放总量和人均碳排放总量均在进行曲折变化，且变化趋势跨度较大，预测未来几年会逐步达到平缓期。

3 因素分解和分析

3.1 因素分解法

kaya Y（1989）提出碳排放量的基本式：

其中，C代表碳排放量；E代表综合能源消费量；G代表工业生产总值；P代表人口数。

图2 2012—2021年苏州碳排放和人均碳排放增长趋势

人均碳排放量为；能源排放强度为 ，即消费单位i种能源的碳排放量（其中，能源结构因素为，即第i种能源在能源总消费中所占的比例）；碳排放系数为 ，即第i种能源的碳排放系数。

能源强度因素为，即单位工业生产值的能源消耗总量（其中，是第j种工业的能源强度）。工业结构因素为，即第j种工业生产值在总生产值中所占的份额；经济发展因素为。

因此，人均碳排放量为：

其中，人均碳排放量取决于SEi（能源结构）、Fi（碳排放系数）、Ij（能源強度）、SGj（工业结构）及R（经济发展）的变化。

并且，第t期相对基期的人均碳排放量的变化量为：

其中，是能源结构因素，是能源排放强度因素；是能源强度因素；是工业结构因素；是经济发展因素；是分解余量。

式（3）中，能源结构因素和工业结构因素需要分别分解，即将式（3）分解成二阶段分解模型：

能源结构是第一阶段的分解因素，得到式（5）：

工业结构是第二阶段的分解因素，得到式（6）：

采用LMDI因素分解法，分别对以上两个模型进行二阶段因素分解。

第一阶段分解结果如下：

其中，。

第二阶段分解结果如下：

其中，。

3.2 2012—2021年苏州碳排放的因素分解分析

本文采用二阶段因素分解分析，对2012—2021年苏州人均碳排放进行因素分解分析，结果如表2和图3所示。

（1）经济发展的贡献份额分析

经济发展影响不稳定，其贡献份额先降后升且处于较高水平。2014—2017年，工业总产值逐年增长，人口也在逐年增长，致使贡献率小于零，在2017年后由负转正，并在2021年经济发展的贡献率达到0.7238吨碳/人。这表明，经济发展仍是碳排放量不断增加的主要原因，如何实现在经济发展的同时，控制碳排放的增长，是需要解决的重要问题。

（2）能源强度的贡献份额分析

能源强度贡献份额总体呈现下降趋势，是抑制苏州碳排放增长的主要原因，其贡献份额在2016年后由正转负，在2021年达到最低值-0.3689吨碳/人。虽然提高能源效率是实现碳排放控制的重要途径，但是单靠提高能源效率并不能完全实现对碳排放的控制，还需要结合其他措施，如推广清洁能源等。

（3）工业结构的贡献份额分析

工业结构贡献份额呈现逐年下降趋势，其调整对减少碳排放的影响越来越大。根据数据可知，工业结构贡献份额处于较低水平，2016年前轻重工业贡献份额基本持平在零附近，2016年之后重工业贡献份额始终大于轻工业贡献份额。这说明，工业结构的优化调整并未对碳排放的改善产生明显影响，因此需要加快推进工业结构调整，尤其是对重工业。

（4）能源结构的贡献份额分析

能源结构贡献份额逐年递减且始终小于零，说明在过去10年，能源结构调整对碳排放的降低起了一定的作用，但该数值不断加深，说明调整的速度和强度不够。经济发展、能源效率和工业结构调整对减少碳排放的影响较大，因此未来减少碳排放的主要方向应是提高能源效率、调整工业结构和加快经济发展。

4 结语

本文采用二阶段因素分解分析法，分析苏州碳排放演化特征及其影响因素，探讨并比较苏州碳排放的时空差异性，据此得出以下结论：

（1）经济发展是碳排放增长的主要因素，其贡献份额在过去10年中总体趋势上升且增长最多，如不加以调整就会不断增加。

（2）能源强度对碳排放的影响不稳定，其总体趋势下降，即对碳排放起到抑制作用。虽然提高能源效率是实现能源消耗强度控制的重要途径，但只提高能源效率并不能完全实现能源消耗强度的控制。

（3）工业结构和能源结构对碳排放的影响趋势同样下降，但相对较小，表明通过产业结构调整抑制碳排放增长的潜力仍有待挖掘。

基于以上研究结论，本文提出以下相应对策建议：

（1）优化经济增长方式，实现经济增长与碳排放的脱钩。完善法律法规和标准体系，如提高能源排放标准、实行碳排放许可证制度等。例如，针对二氧化碳排放量的监管，推动制造企业研发和生产更环保的产品。

（2）通过技术进步，实现能源强度的降低。淘汰老旧设施，革新高能耗设备，减轻煤炭消费，降低高强度碳排放。例如，通过推广高炉煤气制氢技术、新型冶金技术和废钢资源回收利用等技术，降低钢铁生产过程中的煤炭消耗和碳排放。

（3）推进结构性变革，实现能源消费和产业结构的低碳化。减少化石能源消费，推广普及新能源消费，降低高能耗产业比重，发展低能耗产业结构。例如，推广新能源汽车能够减少对石油等化石燃料的依赖，同时减少污染物和碳排放。

参考文献

林晓洁，王长建，汪菲，等.香港地区能源消费碳排放的演变趋势及其影响因素[J].科技管理研究，2022，42（21）：231-238.

姚永玲.北京城市发展中的能源消耗影响因素分析[J].中国人口·资源与环境，2011，21（7）：40-45.

孙燕燕.上海市旅游碳排放估算及其效应分解[J].地域研究与开发，2020，39（1）：122-126.

杨燕，武戈.长三角城市工业碳排放因素分解模型及实证分析：以南京和苏州两市比较分析为例[J].经济研究导刊，2013，204（22）：230-233+258.

孙冬营，王炎霄，丁绪辉，等.长三角城市生活用水量的时空变化与驱动效应研究[J].水利水电技术（中英文），2023（4）：1-19.

纪义虎，左其亭，马军霞.基于Tapio和LMDI模型的沁河流域水资源利用与碳排放关系脱钩分析[J].水资源保护，2023（4）：1-14.

宋辉，黄波，袁征.基于LMDI的中国行业节能机制研究[J].软科学，2019，33（7）：106-110.

张鸿武，王珂英，殳蕴钰.中国工业碳减排中的技术效应：1998—2013年基于直接测算法与指数分解法的比较分析[J].宏观经济研究，2016，217（12）：38-49.

韩钰铃，刘益平.基于LMDI的江苏省工业碳排放影响因素研究[J].环境科学与技术，2018，41（12）：278-284.

龚利，屠红洲，龚存.基于STIRPAT模型的能源消费碳排放的影响因素研究：以长三角地区为例[J].工业技术经济，2018，37（8）： 95-102.

孙义，刘文超，徐晓宇.基于STIRPAT模型的辽宁省碳排放影响因素研究[J].环境保护科学，2020，46（5）：43-46.

Peng Fang. Short-term carbon emission prediction method of green building based on IPAT model[J]. International Journal of Global Energy Issues，2023，45（1）.

王丽，欧阳慧，马永欢.经济社会发展对环境影响的再认识：基于IPAT模型的城市碳排放分析[J].宏观经济研究，2017，227（10）： 161-168.

徐国泉，蔡珠，封士伟.基于二阶段LMDI模型的碳排放时空差异及影响因素研究：以江苏省为例[J].软科学，2021，35（10）：107-113.

Kaya Y. Impact of Carbon Dioxide Emission on GNP Growth： Interpretation of Proposed Scenarios[Ｒ]. Prias： IPCC Energy and Industry Subgroup， 1989.