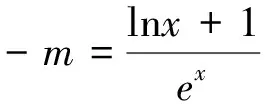导函数零点不可求问题的破解策略
2023-08-26江苏省金湖县第二中学211600梁加林
江苏省金湖县第二中学 (211600) 梁加林
我们在利用导数求函数的单调区间或者极值时,经常会遇到导函数方程f′(x)=0是一个超越方程或是一个含有参数的二次方程,使我们无法求出方程根或者无法清晰的表述方程根的情况,此时我们可能是束手无策,无法继续下去了,其实问题并非是无从下手,而可能是我们知识储备不够丰富,方法研究不够透彻,针对这个常见的解题现象,本文通过对典型例题的分析探求,介绍常用的五种处理手段,供读者朋友参考.
一 赋值探求
如果导函数涉及的是关于lnx的复合函数时,一般可令x=et,特别的是令x=1或者x=e进行试探;如果导函数涉及的是关于ex的复合函数时,一般可令x=lnt,特别的是令x=0或者x=1进行试探求解.
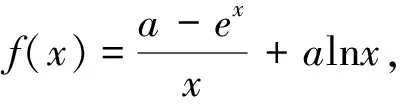
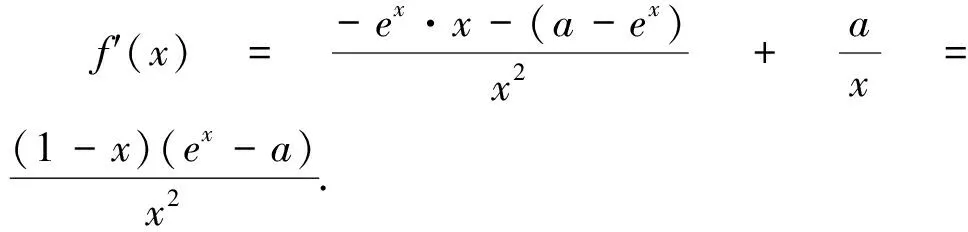
点评:如果导函数方程是超越方程,不应该用常规解方程的方法求解,需要灵活地使用相关的特殊值验算得出,这是一个重要的解题共识.
二 虚设零点
通过假设x0是方程f′(x)=0的根,然后将x0代入方程并设法消去参数,重新构造出关于零点的一个单一函数,这样就能把题目转化为常规的方程问题了.
例2 已知函数f(x)=lnx+x,g(x)=x·ex-1,求证:f(x)≤g(x).
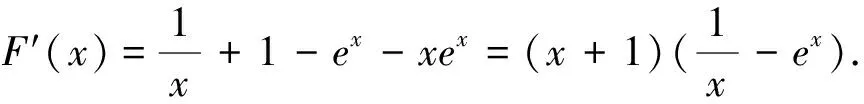
点评:在解题过程中,要时刻记住假设的根的意义和用途,许多情况下,这个假设对后面解题会起到关键作用,如本题中得到了F(x0)=0.
三、多次求导
在通过第一次求导后无法确定导函数的零点,可以设一个新的相关函数并再一次或又一次的求导,这样就使导数式变得越来越简单,为成功解决零点问题化解了难点.
例3 已知函数f(x)=xlnx-ex+1.试证明:f(x) 析解:要证f(x) 点评:多次求导也是导数题中的重要解题技巧,尤其是在含有lnx和ex的函数式中会经常得到使用,而此法是以能够解导函数方程为目的,必须得到正确运用. 在整体形式上很难判断出f′(x)正负和求出零点时,可以采用分离构造函数g(x),使f′(x)=g(x)·h(x),其中h(x)恒正或恒负,这样下一步只需对g(x)进行研究就可以了. 点评:运用此法的目的是使解题过程简化、优化,所以必须先对导函数式进行有效的变形转化,在能确定其中一部分函数式的符号后,再设一个新函数. 如果在直接求导函数的零点难以达到的情况下,可以通过对导函数进行代数变形、整合重组,转化为一个与原题意一致的并且新函数求零点容易解决的问题. 例5 已知函数f(x)=xlnx+mex有两个极值点,求实数m的取值范围. 点评:通过对导函数式的变形,创造了重组的条件,而重组的目的是方便解决下面的问题,如本题中的参数范围,所以重组必须有一部分是比较简单的,这是解题原则. 前面通过典型例题的分析,介绍了导函数零点不可求问题的五种求解策略,其核心就是围绕如何确定相关的超越方程的解所施展的破题手段,而抓住问题特点,精准分析、重点突破是关键.只有在平时的教学过程中注重点解题方法的研究、解题规律的探索,就可使学生思维能力获得较大提高.四 拆分构造
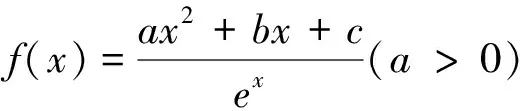

五 整合重组