阿波罗尼斯圆的逆向探究及应用

浙江省宁波华茂高级中学 (315192) 崔华梅 孙续桂 戴宏照

一、提出问题

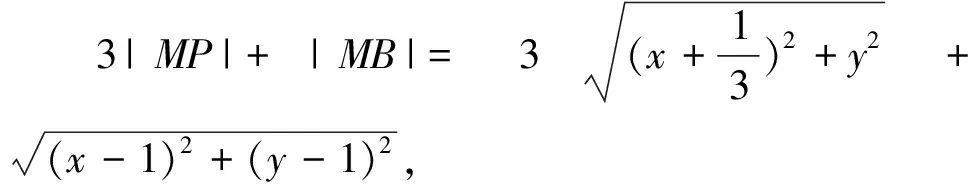
二、阿波罗尼斯圆及逆向探究

平面内到两个定点A、B的距离之比为定值λ(λ>0,λ≠1)的动点的轨迹是圆,称之为阿波罗尼斯圆.在解析几何有关问题中,经常是已知圆的方程,那么,对于一个定圆,A、B两点是确定的吗?

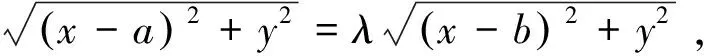
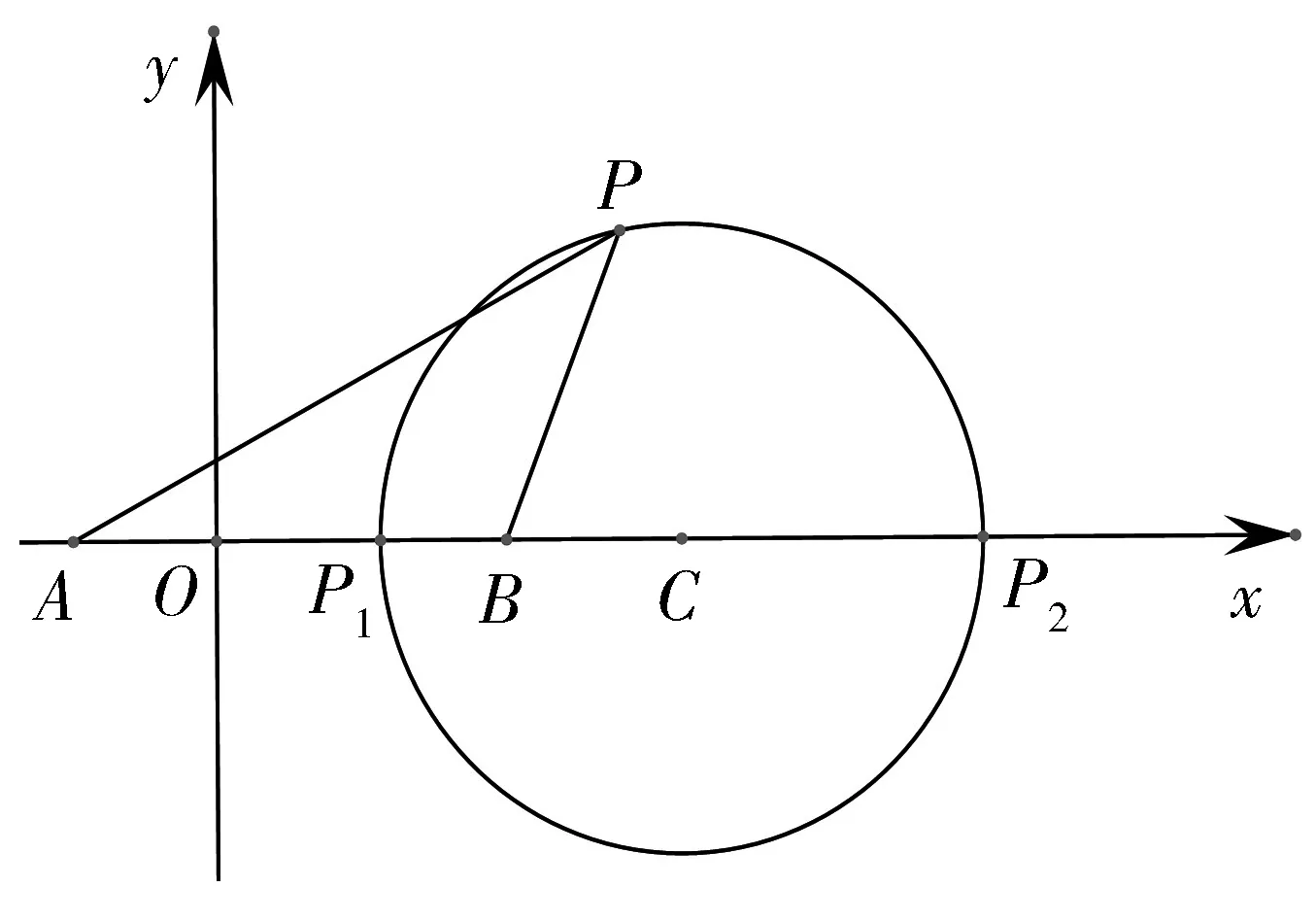
图1

探究1 当圆C和定比λ确定时,A、B两点唯一确定吗?

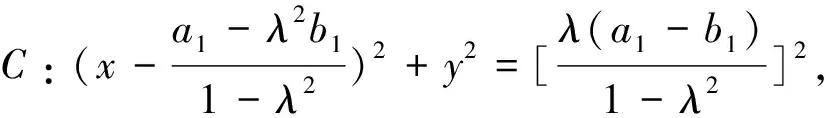
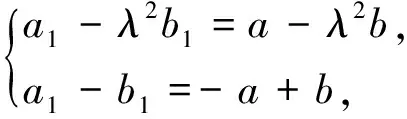
探究2 当定圆和以圆心为端点的射线确定时,比值λ和A、B两点唯一确定吗?

例如对于圆C:x2+y2-8x=0,当|PA|=2|PB|时,A(-4,0),B(2,0);当|PA|=3|PB|

探究3 当定圆与过圆心的定直线交于P1,P2两点时,如果比值λ确定,能否确定A、B两点的坐标?

根据阿波罗尼斯圆的推导过程可知,x1=

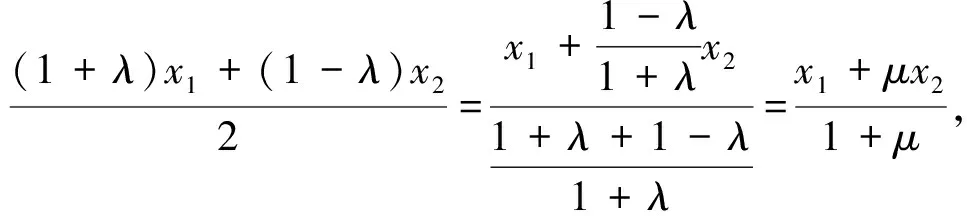
三、问题解决及推广

通过以上探究,我们得到如下结论.

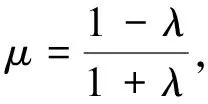
于是,就可以利用过圆心的直线与圆的两个交点坐标求出该圆上任意一点都使|PA|=λ|PB|成立的A、B两点的坐标.下面,我们应用此结论解决一类线段长度之和或向量模之和的最值问题.

因此,求两条线段长度之和的最值问题,如果线段前的系数不相等,就可以考虑用阿波罗尼斯圆逆向求解,先把系数转化成相等的两条线段长,再利用三角形三边的不等关系,继续转化成过这点的一条线段长的最值问题.为了加深理解,我们再看一例:

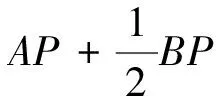
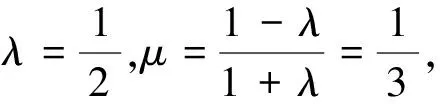
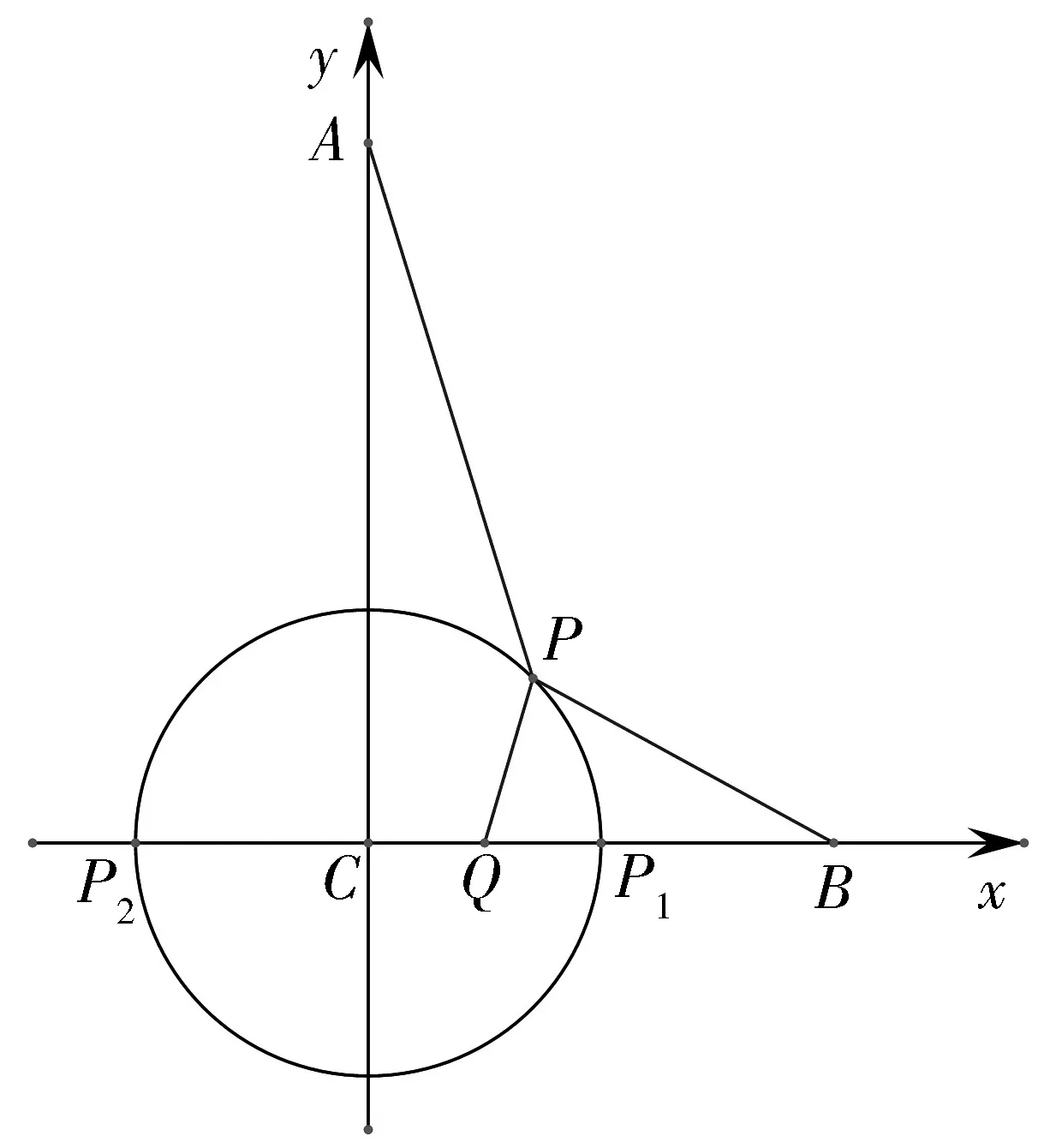
图2

向量的模就是有向线段的长,所以这个结论也用来解决有关向量的模求和的最值问题.

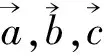
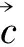
图3

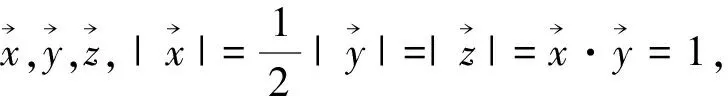
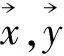
图4

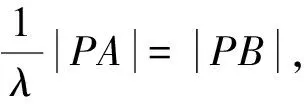
逆向思维有利于破除思维定势,有利于认识数学问题的本质,是创新思维的一种形式;从数学核心素养上讲,阿波罗尼斯圆逆向探究是建立新的数学模型,使数学问题从数学抽象,经过数学推理,易于直观想象.