数学文化融入试题的路径
2023-08-26浙江省象山县第二中学315731
浙江省象山县第二中学 (315731) 林 琪
《普通高中数学课程标准(2020年修订)》,明确指出数学文化应融入数学教学活动,在教学活动中,教师应有意识地结合相应的教学内容,将数学文化渗透在日常教学中,引导学生了解数学的发展历程,认识数学在科学技术、社会发展中的作用.根据数学文化试题背景与数学知识的关联程度,将试题中数学文化的融入方式分为复制式、顺应式和重构式三大类.纵观近年高考,可以发现,数学文化类试题比重逐渐增加,而且每年的高考文化题都充满“数学味”.因此教师应在平时的教学中让学生逐步接触文化类试题,并掌握命题思路.本文以数列为例,论述数学文化融入试题中的路径.
例1 (2022届云南师大附中适应性考试)《九章算术》是我国秦汉时期一部杰出的数学著作,书中第三章“衰分”有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共出百钱.欲令高爵出少,以次渐多,问各几何?”意思是:“有大夫、不更、簪裹、上造、公士(爵位依次变低)5个人共出100钱,按照爵位从高到低每人所出钱数成递增等差数列,这5个人各出多少钱?”在这个问题中,若不更出17钱,则公士出的钱数为( ).
A.10 B.14 C.23 D.26
解析:设大夫、不更、簪裹、上造、公士所出钱数构成递增等差数列{an},公差为d,由题意可知a2=17,S5=5a3=100,∴a3=20,d=a3-a2=3,所以公士出的钱数为a5=a2+3d=26.故选D.
评注:本题以古代数学名著《九章算术》中提出的问题为背景,考查了等差数列基本量的关系式,本题注重考查考生的阅读理解、提取信息、数学建模以及通过计算解决问题的能力,属于基础题.
笔者仿照例1,选取等比数列求某项为知识点,寻找素材,以“毕达哥拉斯树”为背景,尝试命题如下:
例2 毕达哥拉斯树是据勾股定理所画出来的一个可以无限重复的图形,如图1所示.因为形状好似一棵树,被称为毕达哥拉斯树,也叫“勾股树”.毕达哥拉斯树以如下方式生长:以边长为1的正方形的一边作为斜边,向外作等腰直角三角形,再以等腰直角三角形的两直角边为边向外作正方形,得到2个新的小正方形,实现了一次生长;再将这两个小正方形各按照上述方式生长,如此重复下去.则经过10次生长,可形成新小正方形个数为( ).
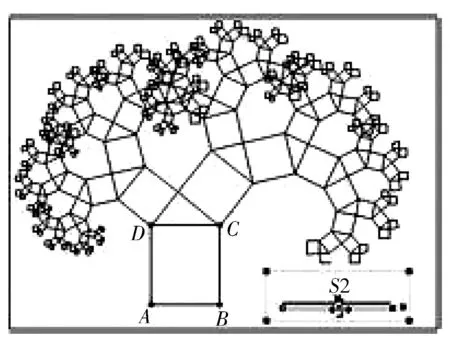
图1
A.128 B.256 C.1024 D.2048
解析:由题意得an+1=2an且a1=2,所以,数列{an}为等比数列,且该数列的首项和公比均为2,因此,an=2n,因此,则经过10次生长,可形成an=210=1024个新小正方形.故选C.
评注:复制式命制试题往往难度较低,前半部分一般都是以论述的形式,给出背景,对之后的解题影响不大,学生很容易找到数学本质,进行求解.
例3(2022长沙市模拟,多选题)对于正整数n,φ(n)是小于或等于n的正整数中与n互质的数的数目.函数φ(n)以其首名研究者欧拉命名,称为欧拉函数,例如φ(9)=6(1,2,4,5,7,8与9互质),则( ).
A. 若n为质数,则φ(n)=n-1
B.数列{φ(n)}单调递增
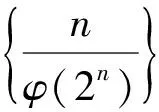
D.数列{φ(3n)}为等比数列

评注:本题以数学文化“欧拉函数”为背景,考查数列的通项及求和、判断数列的单调性、等比数列的判断方法等,考查考生的运算能力和逻辑推理能力,属于中档题.且此题为多选题,考察学生考虑问题的全面性和周全性,选项的设置更是引导考生由浅入深考虑问题.另外,多选题考察的知识点更多,更难,学生不易得全分,这也体现了数学的选拔功能.
笔者仿照例3,选取“冰雹猜想”为背景,考察学生对分段数列求值问题,尝试命题如下:
例4 任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2,反复进行上述两种运算,经过有限次步骤后,必进入循环圈1→4→2→1.这就是数学史上著名的“冰雹猜想”(又称“角谷猜想”),若取正整数m=5,根据上述运算法则得出5→16→8→4→2→1共需经过5个步骤变成1(简称为5步“雹程”)则( ).
A.若m=17,则需要12步“雹程”.
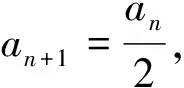
C.若对于正整数m,共需8个步骤变成1,则满足条件的所有m构成的集合为{20,128}.
D.存在连续的两个正整数m1,m2,使得两者的“雹程”一样.
解析:对于A,若m=17,则上述运算法则得出17→52→26→13→40→20→10→5→16→8→4→2→1共需经过12个步骤变成1.对于B,根据题意,显然正确.对于C,可采用逆向思维,所有m构成的集合为{128,21,20,3},如图2.

图2
对于D,由C可知存在连续的两个正整数,m1=20,m2=21使得两者的“雹程”都是8.因此选ABD.
评注:顺应式命制试题往往难度中等,是某一知识点的性质和应用,往往既考察知识点,也考察建模能力,往往比较灵活,学生也容易失分.
例5 (2020·临沂三模)意大利数学家斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,…,即F(1)=F(2)=1,F(n)=F(n-1)+F(n-2),(n≥3,n∈N+),此数列在现代物理、化学等方面都有着广泛的应用.若此数列被2除后的余数构成一个新数列{an},则数列{an}的前2019项的和为( ).
A.672 B.673 C.1346 D.2019
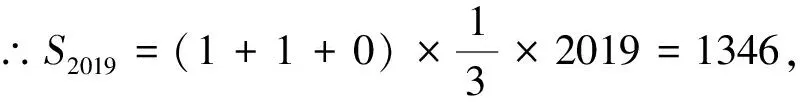
评注:本题以“斐波那契”数列为背景,考察周期函数求和.考察学生阅读理解、数学模型能力,学生需要脱去背景,找到实质是利用斐波那契数列的各项除以2的余数特征,得出新数列的周期性,进而求出结果.属于中档题.另外,此题以著名的“斐波那契”数列为背景,增强了学生对数学史的理解,扩宽了学生的眼界.
笔者仿照例5,在斐波那契数列的基础上加以延伸,以“黄金螺线”为背景,结合扇形的弧长公式,尝试命题如下:
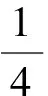

图3
共有7个扇形组成,则整个黄金螺线长度为.
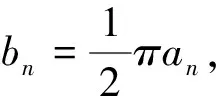
评注:重构式命制试题往往难度较高,是某一知识点或者方法的迁移,常涉及多个知识点,能较好考察学生阅读理解能力、建模能力.
综上分析可见,文化类试题更多考察到学生的阅读理解能力,无论那种命题方式,都应该学会脱去背景,寻找文化背景后的数学考点.教师应在日常教学中经常渗透此类题,让学生更好的经历数学历程、理解数学知识、感受数学思维、体会数学精神.同时,亦可引导学生关注我国社会的进步与发展,增强民族自豪感,增强爱国情怀,培育和践行社会主义核心价值观,实现数学“以德树人”的教育宗旨.
