摭谈数学“潜在优生”变优策略*

江苏省睢宁县第一中学 (221200) 管 勇

数学潜在优生是指那些感官和智力较优,但其数学成绩暂时低于其智力所能及的水平的那部分学生.本文探讨数学潜在优生变优的策略.

1 重视情感教育

富有情感的教育对学生会产生较大的正面影响.俗话说:“良言一句三冬暖,恶语伤人六月寒.”但有些数学教师对学生缺乏情感的投入,不尊重学生,总爱挖苦、体罚、指责学生,特别是对于那些数学成绩不佳的学生,经常当很多学生或教师的面“明嘲热讽”,致使这些智力正常的学生对数学教师产生对立情绪和逆反心理,师生关系紧张,抗拒上数学课,不愿意做数学作业,久之,数学成绩下滑,变成了数学潜在优生.

任何一个人除了衣、食、住、行以外,还有情感的需要,还有被尊重、被认同、被关心和被帮助的需要,所以对学生要给予足够多的信任、宽容、包容、关爱、激励、欣赏、理解、肯定和帮助,建立和谐融洽的师生关系.

当学生取得进步时,教师要给予“公开”鼓励表扬,让学生体验到被欣赏、被肯定的愉悦感、成就感,增强学好数学的信心;当学生做错题、做错事时,应“私下”批评,并动之以情,晓之以理,避免“当众”指责,避免因生气而说出一些挫伤学生自尊心的话.让数学潜在优生能感受到数学教师的可亲可敬,必要时还可对数学潜在优生进行面批面改面指导,让数学潜在优生感受到来自数学教师的“更多”的情感支持,进而喜欢学习数学,变为优生.

2 重视非智力因素的培养

想要数学潜在优生变优,必须重视培养他们克服困难的意志、毅力等,磨炼出持之以恒的良好品质,激发学好数学的斗志、热情和兴趣,驱散数学学习过程中过度的焦虑、茫然、烦躁、不安、紧张等生理上和心理上的不良情绪,提高抗击因数学成绩不理想或下滑带来挫败感的能力,增强数学成绩可以提升的信心,以愉快的情绪、活泼的性格、饱满的热情、宽阔的胸怀投入到数学学习中去.

3 重视学法的指导

“学法不当”是数学潜在优生的一个重要成因.比如,不预习或不会预习,不会听课,不会记课堂笔记,不重视基础知识、基本方法技能和基本活动经验的牢固掌握,不重视解题后反思、归纳和整理,不擅于复习回顾,没有错题本,死记数学结论、解题类型,没有阅读数学教材的习惯或不擅于阅读,解题不规范,不掌握考试技巧,不能批判性地对待教师所讲或课本上所给的解法、结论等等.在教学中,教师应经常性地对学生进行数学学法指导,让学生变得会学数学,从而变优.

4 重视发挥学生主体作用

课堂上,有些数学教师爱搞“一言堂”“满堂灌”,对学生不放心,不让学生阅读、探究、讨论,学生总是被动接受,造成对数学知识方法“消化不良”.对于较难理解的数学概念、数学思想方法,教师的讲解变得责无旁贷,而且要讲透、讲够,好让学生少走弯路;而对于较易理解、学生独立思考就可搞懂的教学内容,完全可以放手让学生自主学习,给学生独立思考时间和空间,让学生既能学进去又能讲出来,擅于讨论、探究,成为课堂主角,发挥主体作用,教师再“以学定教”,这样学生学到的知识、方法,才能理解深刻,记忆长久,才能让数学潜在优生变优.

5 重视“一题多法”解题教学

一题多法教学可训练学生运用不同方法解决同一个问题的能力,提高学生对问题、方法的本质的认识,这对数学潜在优生变优尤其有用,因为“一题多法”可放慢教学节奏,让学生有充分时间体会、质疑、比较和批判,加深对基础知识、基本方法技能和基本活动经验的理解.

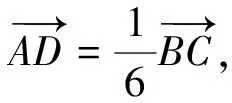
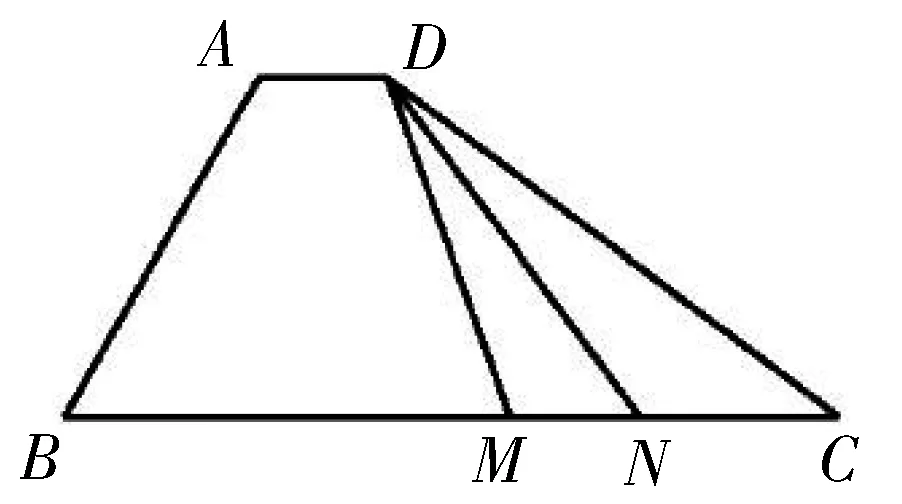
图1

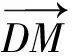
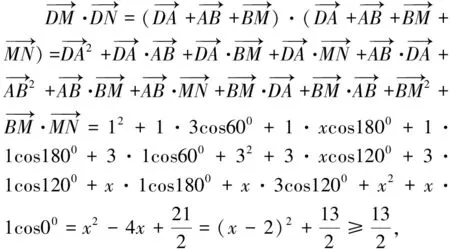
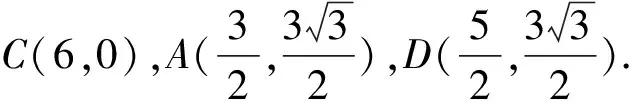
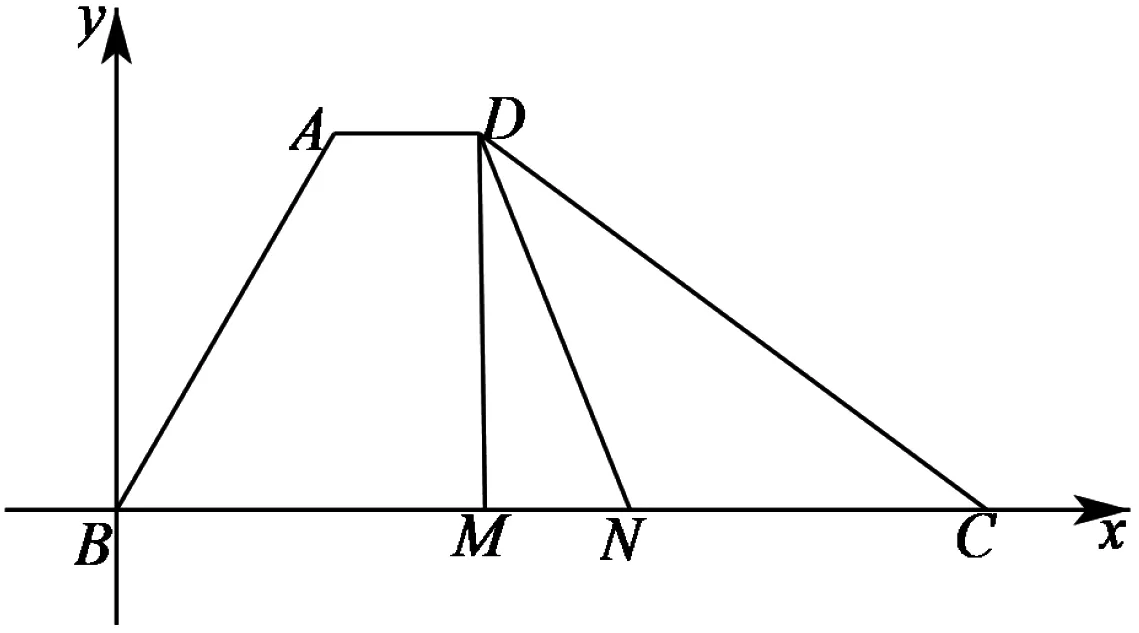
图2

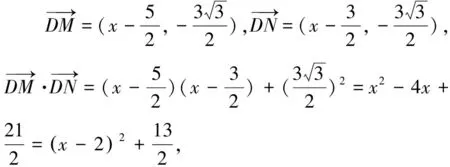
点评：上述解法一先利用向量加法法则进行转化,然后再利用向量数量积的定义求解,在此法解题过程中,常因两向量夹角大小判断错误而功亏一篑;解法二通过建立合适的坐标系,利用坐标法求向量数量积,此法简单,不易出错.此题不宜用基底法,解题时,要用批判性思维选择合适的求法.持之以恒地进行优法采撷,对培养学生的高阶思维能力,特别是批判性思维能力,具有不可小觑作用.

6 重视暴露易错题的解题过程

在数学解题教学中,数学潜在优生往往听得“津津有味”,似乎“懂了”,但自己解题时往往不知如何下手.在进行解题教学时,若教师能重视暴露解题过程特别是学生易错的解题过程,并引导学生亲身感受、体验解题思路的探究过程和纠错的过程,让学生“知其然,且知其所以然”,则可让学生有效规避易错的解题方法,久之,数学潜在优生不但听得“懂”而且“会”做题,久之,必可变优,且批判性思维也会得到培养.

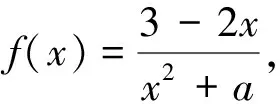
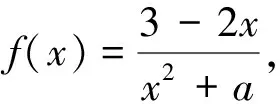
x(-∞,-1)-1(-1,4)4(4,+∞)f′(x)+0-0+f(x)增极大值减极小值增

画草图,如图3,所以f(x)无最大值和最小值.

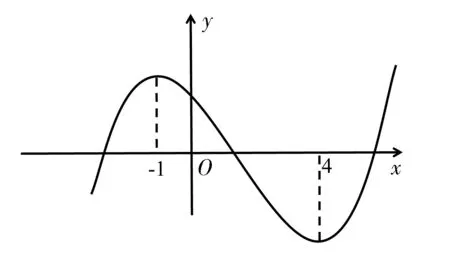
图3

剖析：上面解法有两处错误.

错误一：求出a值后没有验证,虽然此题验证后没有舍掉a值,但“验证”这一步不可少,数学解题中的推理要讲究“严密性”“严谨性”,要确保每一步的转化都是等价的.

事实上,当导函数f′(x)在x=x0处有意义时,则f′(x0)=0是函数f(x)在x=x0处有极值的必要不充分条件,而不是充要条件.也就是说,若函数f(x)在x=x0处有极值,且导函数f′(x)在x=x0处有意义,则一定有f′(x0)=0;但是当f′(x0)=0时,x=x0不一定是函数f(x)的极值点:当x=x0是方程f′(x)=0的偶次重根时(即在x0的左、右两边附近f′(x)同号),则x0不是函数f(x)的极值点;当x=x0是方程f′(x)=0的非偶次重根时(即在x0的左、右两边附近f′(x)异号),则x0才是函数f(x)的极值点.只要在求出a值后,若写上“经验证,当a=4时,在x=-1左右两边附近f′(x)异号,所以函数f(x)在x=-1处能取得极值,符合题意”,则解题过程完善严谨!

错误二：草图过“草”,导致错误判断函数f(x)无最大值和最小值.数形结合思想应用得当,有时可达事半功倍之效,但应用不当,即画图不准或太过随意性,则会事倍功半,甚至前功尽弃.

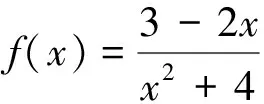
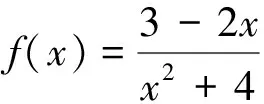
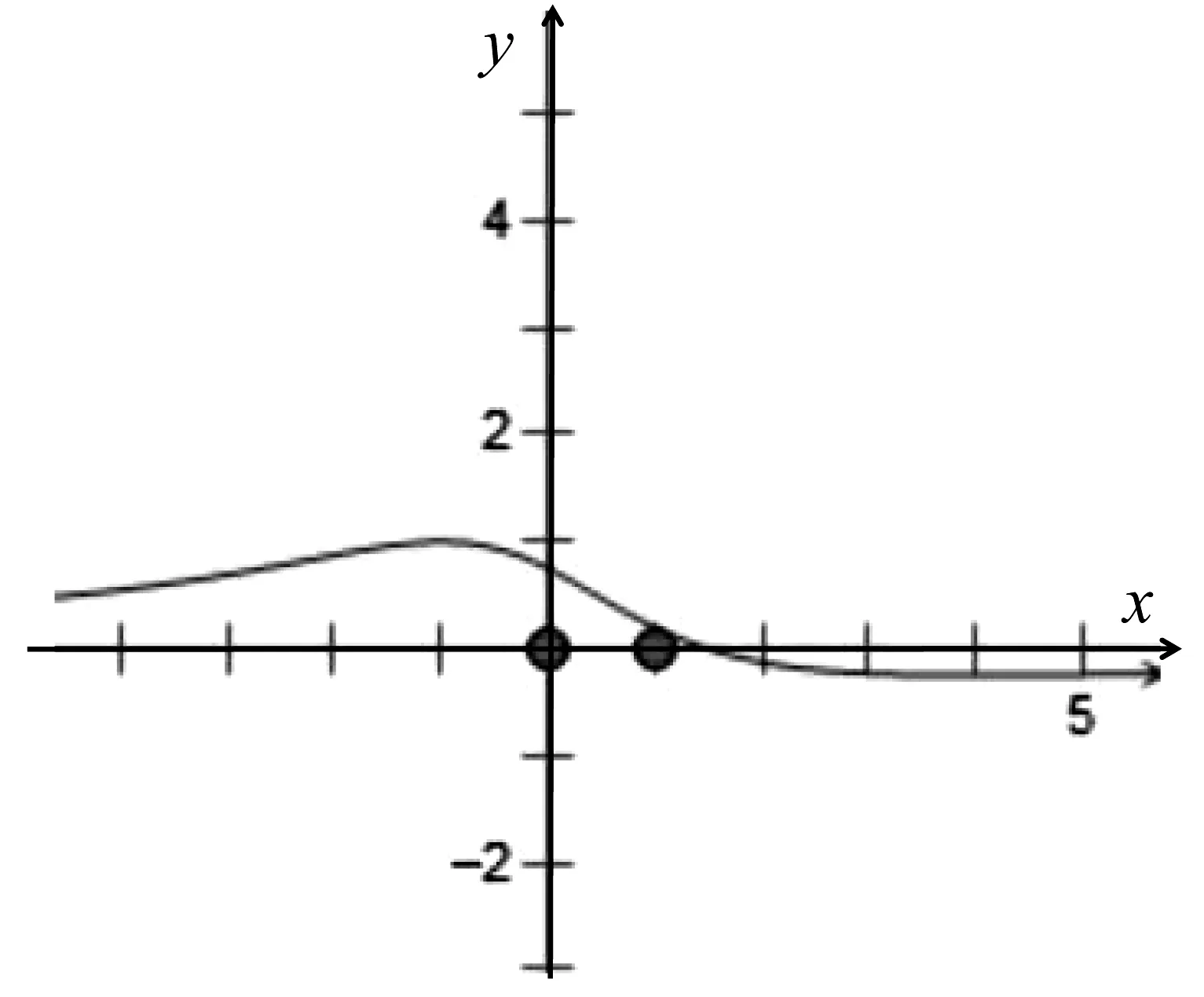
图4

另外,重视变式题教学、重视数学思想与方法的渗透、重视数学思维能力培养、重视引导和启发、重视知识建构过程、增强责任心、因材施教、分层教学、个别课后辅导,…,等等都是数学潜在优生变优的有效教学策略.