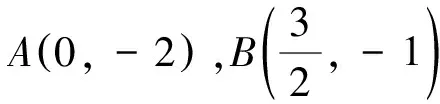妙用“三化”提升解题效益
2023-08-26福建省漳州第一中学363000林志展
福建省漳州第一中学 (363000) 林志展
“三化”是指特殊化、极限化、一般化.通过“三化”解题,可化难为易,化繁为简,避免“小题大做”,甚至实现“大题小做”.
本文结合历年全国卷的高考试题,谈谈“三化”在解题中的应用,供大家参考.
1 运用“三化”快速准确选定结果
由于解答选择题与填空题无须在卷面上书写解答过程和理由,因此为了提高作答速度,一般通过取特殊值,特殊点,特殊函数,特殊方程,特殊图形等进行简单的运算、推理或判断,可快速得到问题的答案,或者否定错误的选择支.
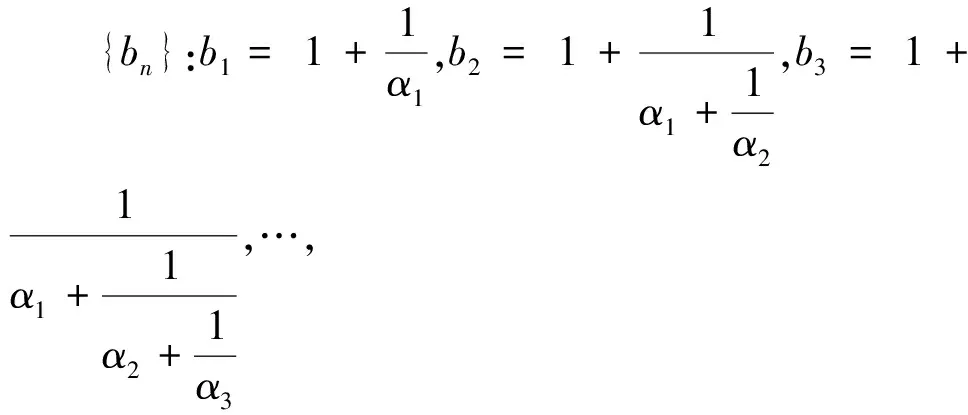
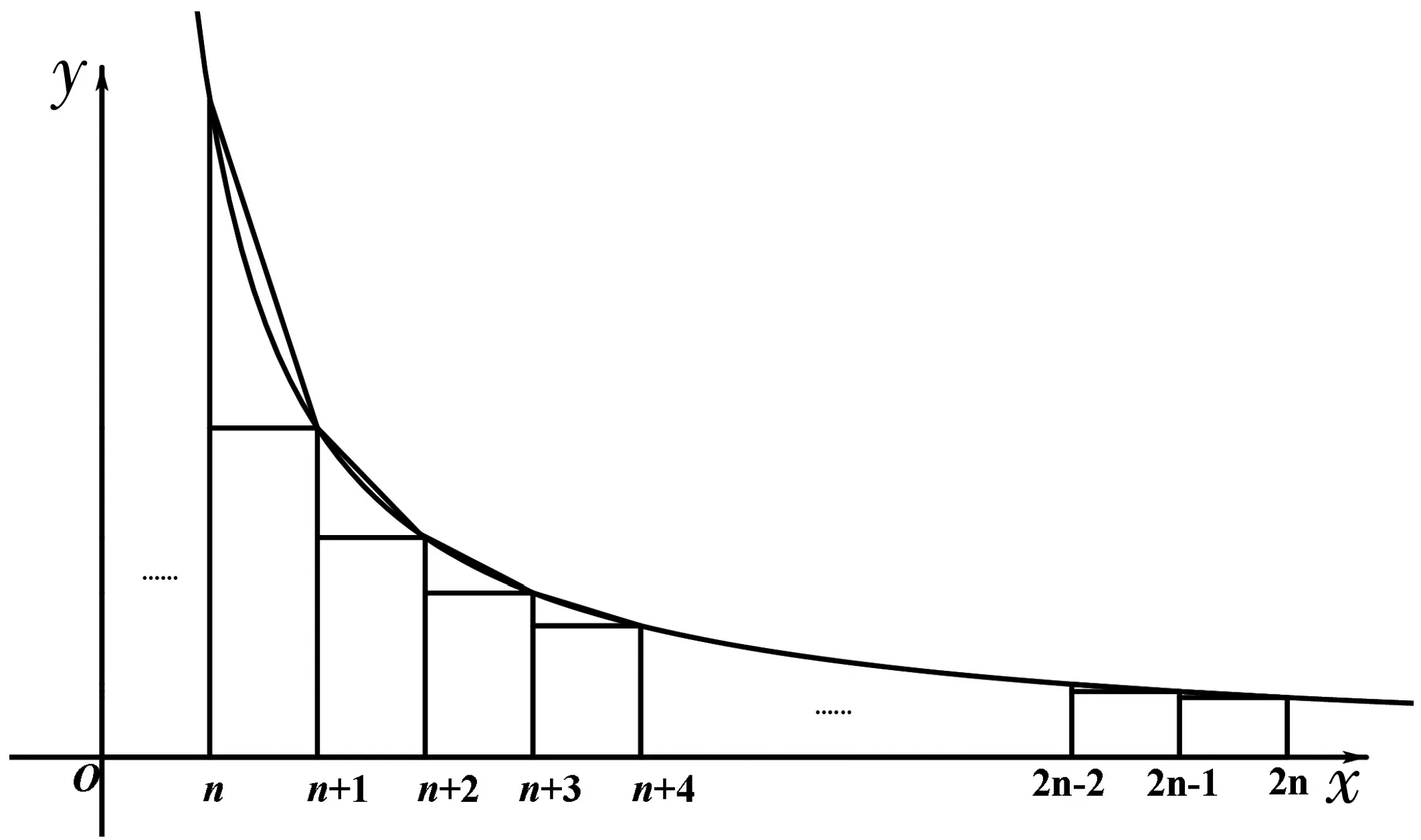
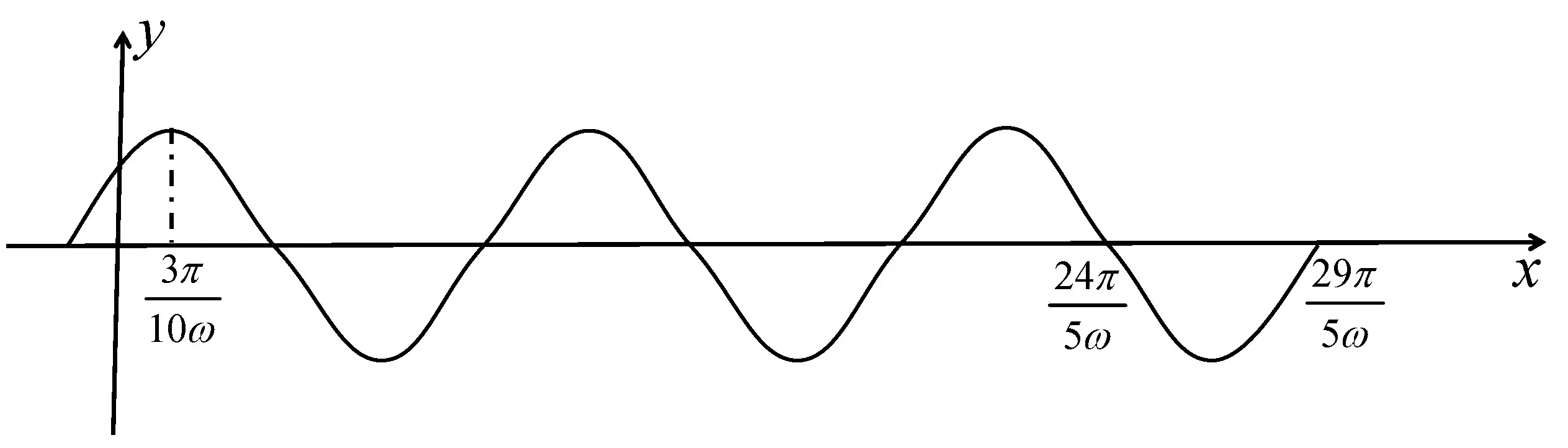
A.b1 A.-3 B.-2 C.0 D.1 例3 (2023年四省联考,第8题)已知a,b,c满足a=log5(2b+3b),c=log3(5b-2b),则( ). A.|a-c|≥|b-c|,|a-b|≥|b-c| B.|a-c|≥|b-c|,|a-b|≤|b-c| C.|a-c|≤|b-c|,|a-b|≥|b-c| D.|a-c|≤|b-c|,|a-b|≤|b-c| 分析与解:题目有三个变量,有关于三个变量的两个方程,如果给定其中一个变量的值,那么另外两个随之确定.由于a,c都可用b表示,又注意到b的范围是(0,+∞),为此令b→0,则a→log52>0,c→-∞,则|a-c|≥|b-c|,|a-b|≤|b-c|,选择B. A.①④ B.②③ C.①②③ D.①③④ 分析与解:由于题中函数f(x)是由解析式给出,为了理解题意,我们通过伸缩变换做出f(x)的图象,如图1. 图1 图1 为了理解问题,寻找解法,我们必须回到片面情况、具体情况、特殊情况甚至极限情况,将问题以直观的形式呈现,从不同视角理解题意,明确这道题的解题方向,但具体到解答步骤,还是要回到数学的抽象表达,运用严密的数学推理. 下面只需验证:当直线MN的斜率存在时,直线HN过定点A(0,-2). 综上,直线HN过定点A(0,-2). (1)若x≥0时,f(x)≤0,求λ的最小值; 从上面几道高考题可以看出,善用“三化”解题可化难为易,化繁为简,避免“小题大做”,甚至实现“大题小做”.特别地,对于没有思路或等价转化后不易求解的问题,我们可考虑利用“三化”寻求解题思路或者优化解答的过程,往往能使解题峰回路转,或达到事半功倍的效果.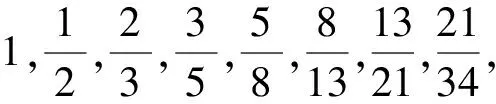
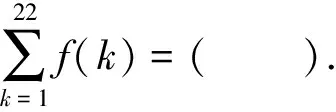

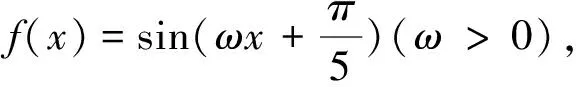
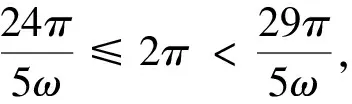
2 运用“三化”为问题的证明提供方向