基于“问题链”情境下的习题教学
2023-08-26安徽省砀山中学235300盖传敏宋永清
安徽省砀山中学 (235300) 盖传敏 宋永清
在复习备考中,除了复习梳理知识点外,习题教学是必不可少的一个重要环节.在以往的习题教学中,都是老师拼命地讲,学生努力地听,师生彼此陷入了“教师担心讲不到位,学生担心练不全面”的焦虑之中.如何真正地让师生从题海中走出来,实现双减的目标,是笔者一直在思考的问题.在近期的课堂教学中,笔者通过尝试设置适当的问题链,在问题链的引领下进行教学,可指导学生进行深度学习.本文结合教学中的典型习题谈谈基于“问题链”情境下如何进行有效教学.
一、通过设置启发式问题链确定解题方法
在习题教学中,当学生遇到解题障碍时,我们教师不应急于给出正确的解题答案,而应从宏观的角度给学生指明解题方向,可通过设置启发式问题链唤醒学生的已有认知,引导学生确定解题方法,明确解题方向.
例1 (2022年新高考全国Ⅱ卷12题,多选题)对任意x,y,x2+y2-xy=1,则( ).
A.x+y≤1 B.x+y≥-2
C.x2+y2≤2 D.x2+y2≥1
分析:该题是有关二元变量的取值范围问题,融基础性、综合性和创新性于一体,解法灵活多样,是很好的一道练习题,可同学们却在求解时四处碰壁,不知所措,下面通过设置启启发诱导形式的问题链引导学生从三个不同的角度进行求解.
问题1 能否利用不等式性质建立选项与题设条件之间的联系?
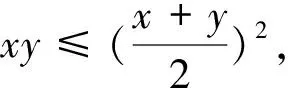
点评:运用不等式性质求解的关键是将已知条件进行适当的配凑,建立已知与未知之间的联系.
问题2 能否将双变量问题转化为单变量问题?
分析:直接消参无从入手,能否利用换元法将双变量转化为单变量?
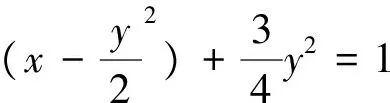
问题3 能否挖掘出该题的几何背景,利用几何意义进行求解.
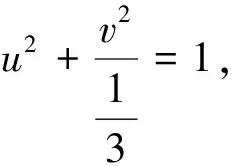
点评:此解法的关键是通过换元把已知条件转化为椭圆标准方程形式,进而借助几何意义求解,方法快捷有效.
二、设置递进式问题链厘清解题思路
在习题教学中,对于一些难度较大的试题,学生一时很难厘清解题思路,即使听老师讲解也很费力.这时若能根据学生的认知水平,把复杂问题进行分解,通过环环相扣递进式地设置问题链,循序渐进地帮助学生消除思维障碍,这样学生接受起来较为轻松,同时可消除学生学习数学的畏难心理,增强学生学习数学的信心.
例2 (2020课标Ⅰ理11题)如图1,已知⊙M:x2+y2-2x-2y-2=0,直线1:2x+y+2=0,P为l上的动点.过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( ).
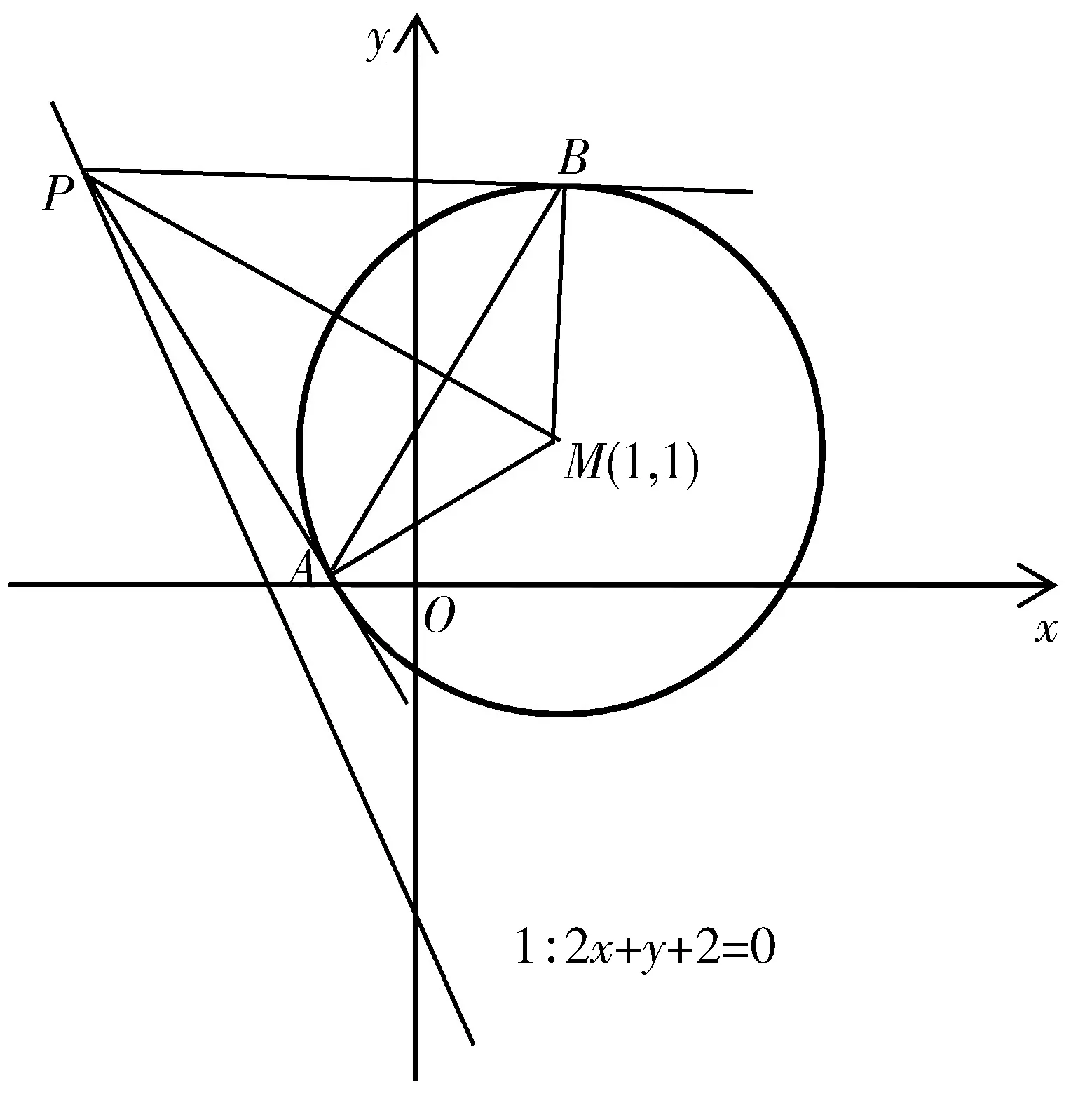
图1
A.2x-y-1=0
B.2x+y-1=0
C.2x-y+1=0
D.2x+y+1=0
分析:该题作为高考压轴题,综合性强,难度大,学生一时找不到正确的解题思路,但认真思考后会发现,该题可分解成若干个小问题进行求解,通过设置递进式问题链的形式将“大事化小,小事化了”.
问题1|PM|·|AB|的几何意义?

综上所述,本施工方案在工期上节省了每道工序的超前管棚施工时间和吊罐出渣时开挖等待时间;在投资上节省了管棚钢管材料费,且减少了门机、吊罐、门机操作人员、人工开挖人员等的投入;在安全方面,减少了吊装设备、钢丝绳等危险源,避免了安全事故的发生。
问题2 如何求解四边形PAMB的面积SPAMB?
分析:四边形PAMB是一个不规则的四边形,在求解四边形PAMB的面积时,不妨采用分割法,即SPAMB=S△PAM+S△PBM.又因为△PBM≅△PAM,所以S△PAM=2S△PAM.
问题3 如何求S△PAM面积的最小值?
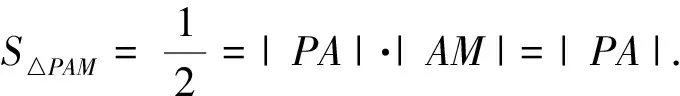
问题4 过点P(-1,0)作⊙M的切线PA,PB,切点为A,B,如何求直线AB的方程?
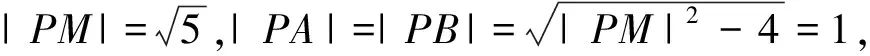
方法二:(利用同构求解)设A(x1,y1)B(x2,y2),则⊙M在点A处的切线方程为(y-y1)(y1-1)+(x1-1)(x-x1)=0,因为切线过点P(-1,0),将点P(-1,0)代入可得2x1+y1+1=0①,同理可得2x2+y2+1=0②,由①②可得直线AB的方程为2x+y+1=0.
三、设置发散式问题链拓展学生思维
例3 (2018年全国Ⅰ卷文20题)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.(1)当l与x轴垂直时,求直线BM的方程;(2)证明:∠ABM=∠ABN.
分析:本题难度适中,大部分同学能很快得到正确答案.在课堂教学中,如果就题论题,简单帮助学生厘清思路,给出答案,那就显得操之过急了.这时如果能够通过问题链的形式将该题进行发散延伸,不仅可帮助同学们理解问题本质,还能促进学生思维的深层发展.类比发现新的问题.
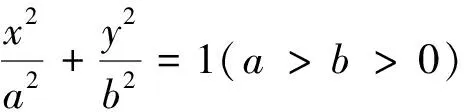
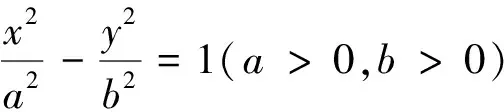
问题3 已知抛物线y2=2px(p>0)上两点A,B(不关于x轴对称),点N(-m,0)(m>0),若∠ANO=∠BNO,证明:直线AB恒过定点M(m,0).
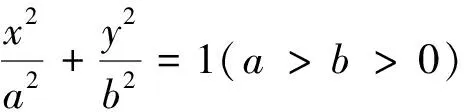
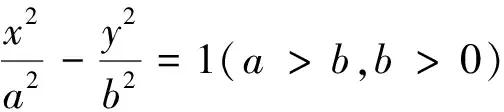
结束语问题是数学的心脏,不论是新课讲授还是习题教学,我们都可通过设置问题链的形式培养学生发现问题、提出问题、分析问题和解决问题的能力.通过问题链教学还能激发学生的内驱力,引导学生从“想学”到“学会”,再到“会学”的跨越.除此之外,作为一线教师我们要不断地探索和创新教学模式,通过我们的努力,让学生会学数学、热爱数学,同时感悟数学的科学价值与应用价值.
