Arbitrary Decode-Forward Relaying with Re-Encoded Bits Selection Strategy for Polar Codes

Di Guan,Kai Niu,Chao Dong

Key Laboratory of Universal Wireless Communication,Ministry of Education,Beijing University of Posts and Telecommunications,Beijing 100876,China

Abstract: In this paper,we propose an arbitrary decode-forward single-relay scheme for finite blocklength polar codes,which can be applied to the general symmetric discrete memoryless relay channel with orthogonal receiver components.The relay node decodes the received message.The relay node selectively re-encodes the message and transmits it to the destination node.Furthermore,in order to minimize the upper-bound of the block error probability,we propose a selection strategy to decide the proper re-encoded bit set by the relay.Simulation results are presented to illustrate the improvement in decoding performance of the proposed scheme compared to conventional relay schemes in both additive white Gaussian noise(AWGN)channel and Rayleigh fading channel(RFC).

Keywords: polar codes;decode-and-forward relaying;arbitrary relay channel;block error rate estimation

I.INTRODUCTION

Polar codes,proposed by Arıkan [1],were proved to achieve the symmetric capacity of the binary-input discrete memoryless channels (B-DMCs) under the successive cancellation(SC)decoder.For a given code rate and code length,the most reliable bit subchannels are used to carry the information bits.In order to construct the polar codes,one needs to calculate the reliabilities of all the bit subchannels.Several works have been proposed to obtain the reliabilities for the bit subchannels in any BDMC,of which density evolution[2]is adopted while having a relatively high computation complexity.Gaussian approximation (GA)algorithm,a simplified version of the density evolution,is proposed in [3] to construct the polar codes in the binary input AWGN channel(BIAWGNC).For other channels,such as the Rayleigh fading channel(RFC),the average mutual information(AMI)equivalence method[4]can be applied to construct the polar codes.In[5],parity-check-concatenated(PCC)is proposed.In addition,with the heuristic construction proposed in the paper,the PCC polar codes have evident performance gains over the cyclic redundancy check(CRC)-concatenated polar codes.In[6],a new framework for constructing polar codes based on the genetic algorithm(GenAlg)is proposed and achieves the same error-rate performance as the CRC-aided SCL decoding over both the AWGN channel and the Rayleigh channel,respectively without CRC-aid.As for high reliability polar decoding methods,successive cancellation list (SCL) [7,8] decoders aided with the CRC[9] were introduced to improve the decoding performance of polar codes.

In [10],it was proved that polar codes are applicable for the degraded wiretap and relay channels and outperform the performance of LDPC codes.In[11],polar codes were designed for degraded relay channels.In[12],construction methods of polar codes for both decode-forward(DF)and compress-forward(CF)relaying were proposed.In [13],a smart decodingforward relaying was proposed to further improve the decoding performance.However,these schemes are designed for physically degraded relay channel.In[14],a decode-forward relaying scheme in the singlerelay channel was developed,which achieves full theoretical rates in general relay channels with an infinite block length.Nevertheless,to the best of our knowledge,polar coded DF relaying with finite block length for general relay channel is still an open problem.

In this paper,we propose an arbitrary decodeforward relaying by using polar codes with finite block length.The relay determines whether to transmit information to the destination based on the decoding results of the CRC-aided polar decoder.If the decoding results at the relay node pass the CRC check,the relay node selects part of the decoded information bits and re-encode them.The re-encoded bits are transmitted to the destination to assist the decoding of the original information.We derive the upper-bound of the block error probability of the proposed method.Furthermore,according to the estimation of the decoding error probability,a re-encoded bits selection strategy is applied.The proposed strategy figures out the bit sub-channels corresponding to the proper re-encoded bits first,and then it determines the re-encoded bit set.

Throughout this paper,boldface uppercase (lowercase)letters are used to denote the matrices(vectors).Sets are represented using calligraphic letters.Given a vector u=(u1,...uN)and a setA ⊂{1,...,N},the notation uAdenotes the sub-vector of u consisting of elements inA.Acdenotes the complementary set ofA.Let u=(uA,uAc)denote that the vector u consists of two concatenated sub-vectors uAand uAc.Given an eventε,its complementary event is denoted as.C⊗ndenotes then-th Kronecker product of the matrix C.

The remainder of the letter is organized as follows.Section II gives a brief description of polar codes.The proposed arbitrary decode-forward relaying for polar codes is described in Section III followed by the analysis of decoding error performance.A re-encoded bits selection strategy is addressed in Section IV based on the estimation of the block error probability.Section V describes the simulation results.Finally,Section VI concludes the paper.

II.PRELIMINARIES AND NOTATIONS

In this section,we provide a description of the system model of the RFC and the polar codes.

2.1 System Model

In the RFC,the received signal can be given as follows

wheres(b)=1−2b,b ∈{0,1}is the channel input,andnis a Gaussian noise with the mean 0 and the varianceσ2.The channel parameterhobeys the independent Gaussian distribution and the envelope of that obeys the Rayleigh distribution.Whenh=1,RFC degenerates into AWGN channel.

2.2 Polar Codes

III.ARBITRARY DECODE-FORWARD RELAYING

In this section,we propose an arbitrary decodeforward (ADF) relaying based on polar codes for the RFC.We provide detailed description of the ADF relaying method,and the performance analysis is addressed following.

3.1 Arbitrary Decode-Forward Relaying Design

According to [4],we apply the average mutual information equivalence (AMIE) method to transform the RFC into an equivalent BIAWGNC.The main concern of the AMIE method in[4]is to find an equivalent BIAWGNC with the same AMI as the RFC as

Firstly,we give an overview of the structure of the ADF relaying.

As shown in Figure 1,the ADF relaying contains a source nodeS,a relay nodeR,and a destination nodeD.The source-relay channelW(ySR|x) is denoted asWSR,where x=(uA,uF)GNis theN-length transmitted codeword,and ySRis the received message at the relay node.The information bit set and the frozen bit set are denoted asAandFrespectively.The relay-destination channelW(yRD|xR)is denoted asWRD,where xR=(uB,uBc)GNis the re-encoded codeword transmitted at the relay node,and yRDis the received message at the destination node.The reencoded bits denoted by uBare selected according to the decoding resultsat the relay node,whereBdenotes the re-encoded bit set.The re-encoded bit setBis selected to minimize the error probability of sourcedestination channelWSD,that is,

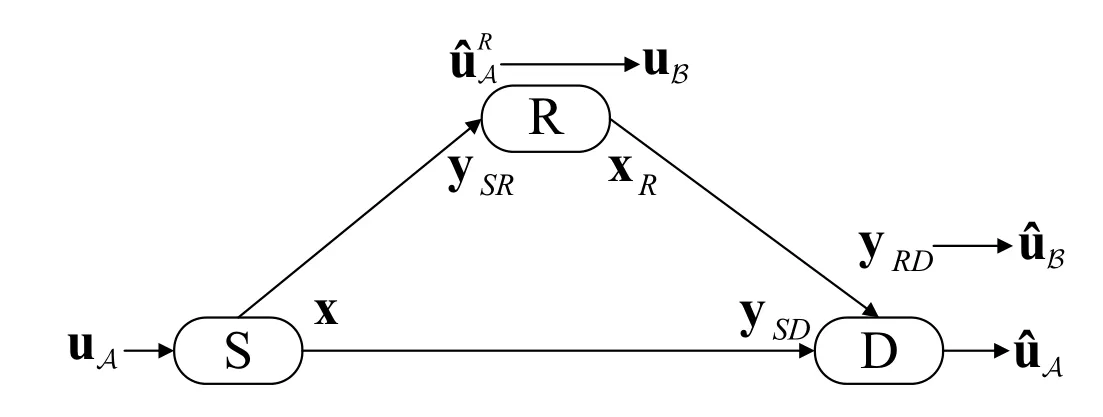
Figure 1.Structure of the ADF relaying.

Based on the symbols defined above,we provide a high level description of the ADF relaying as following:

1.Source node polar encodes the original information into codeword x;

2.Source node broadcasts x to relay node and destination node;

3.Relay node receives message ySRand performs polar decoding.The decoding results are selected byBand re-encoded into xRand transmitted to destination node;

4.Destination node performs polar decoding according to the received messages ySDfrom source node and yRDfrom relay node and obtains the decoding results.

The information bits setAand frozen bits setFare obtained according to channelWSDby the GA.The re-encoded bits setBcan be calculated online or off-line by Eq.(4),which is known to the relay node and the destination node during the ADF decoding.The source node encodes the information vector uAto codeword x and broadcasts x to the relay node and the destination node.The received messages at the relay node and the destination node from the source node transmission are defined as ySRand ySDrespectively.The relay node performs re-encoding on the received message ySR,and select the re-encoded bits from the decoding results according toB.The re-encoded codeword xRis transmitted to the destination node.At the destination node,decoding resultsare obtained by polar decodings on received messages ySDand yRD.

Two algorithms are provided to give detailed descriptions of the processes at relay node and destination node.

In Algorithm 1,the detailed description of the reencoding processes at the relay node is provided.The relay node performs a CRC-aided polar decoding on the received message ySR.If the decoding results pass the CRC checking,the relay node re-encodes the decoding results as xR=(uB,uBc)GNand transmit xRto the destination node.On the contrary,if the decoding results fail to pass the CRC checking,the relay node remains silent.

In Algorithm 2,the polar decoding performed at the destination node are introduced.The destination node performs CRC-aided decoding on the channel outputs ofWRD.The decoding bits are viewed as frozen bits if they pass the CRC checking.Thus,the frozen bit set of u is updated asFD=F∪B.Then the destination node decodes the received message from channelWSDand obtain the decoding resultsuAB.Otherwise,the destination decodes the outputs of channelWSDwithFas frozen bit set and obtain the decoding results.

Based on the algorithms above,we provide a summary of the ADF relay processing as follows.Firstly,the source node polar encodes the original information and broadcasts the encoded message to the relay node and destination node.At the relay node,message transmitted from the source node is decoded.If the decoding results pass the CRC check,the relay node will re-encode part of the decoded bits and transmit the reencoded message to the destination node.Otherwise,the relay node remains silent.At last,the destination node performs CRC-aided decoding on the transmitted codeword from the relay node.If the decoding results pass the CRC check,it will be viewed as frozen bits and help the decoding of the message from the source node.Otherwise,the destination node discards the message from the relay node and performs a direct polar decoding on the message from the source node.

3.2 Analysis on Decoding Performance

We now provide an estimation of the decoding performance of the ADF relaying scheme.To simplify the analysis,we use an oracle-ADF(ORA-ADF)relaying model.In this model,we assume that the relay node and the destination node always know that whether the received messages are correctly decoded.In realistic scenarios,blind detection [15,16] can be applied to figure out if the decoding results are correct or not.

Letεdenote the error event of SC decoding of the original message by the ORA-ADF with the relay node working,andP(ε)denote the probability of the event.LetεSD,εSRandεRDdenote the error event of SC decoding of the transmitted information overWSD,WSRandWRDrespectively.

Proposition 1.For the ORA-ADF relaying with orthogonal receiver components,P(ε)≤ P(εSD)holds for arbitrary symmetric discrete memoryless relay channel.

Proof.For the ORA-ADF relaying with orthogonal receiver components,we have

Since in ORA-ADF relaying,the relay node and the destination node always know that whether the received messages are correctly encoded.Therefore,we haveP(εSD)=P(ε|εSR) andP(εSD)=P(ε|εRD).Substituting the equations into Eq.(5)and Eq.(6),we derive that

It is proved that in arbitrary relay channels with orthogonal receiver components,the decoding performance of the proposed ADF is not worse than that of the decoding that only uses the message from the source node.

IV.RELAY RE-ENCODED BITS SELECTION STRATEGY

In this section,we propose a relay re-encoded bits selection strategy that based on the error probability estimation of polar codes.This strategy can figure out the proper set of re-encoded bitsBwith acceptable computational complexity.

We designate the candidate re-encoded bit set withkre-encoded bits as

to denote the incremental error rate when the reencoded bit setB′is added a new sub-channel indexik.

Proposition 2.For the ADF relaying,start from B′=∅and k=1,add ik into B′ till it satisfies δ(B′)≥0,so that the proper re-encoded bit set is obtained as B=B′.

Finally,the algorithm outputsB′as the proper reencoded bits set.

As shown in the algorithm,an iterative method is applied to search the reasonable re-encoded bit setBwith O(K) computational complexity.Compared to the brute-force search which takes O（K2）calculations,the strategy we proposed reduces the online computational complexity with a negligible performance loss.

V.SIMULATION RESULTS

In this section,we provide the simulation results to verify the advantage of the proposed ADF relaying in both AWGN channel and RFC.The polar codes with the code lengthN=512 and the information bit lengthK=256 are applied.8-bit CRC codes are applied at the relay node and the destination node to check if the received message is correctly decoded.For the AWGN channel,the polar code is constructed by the GA method according to channelWSD.For the RFC,AMI equivalence is applied to construct the polar code based on the GA algorithm.The ADF relaying applies the re-encoded bits selection strategy (RBSS).For ADF relaying without this strategy,the relay node selects the re-encoded bits number asKR=128.SC decoder and SCL decoder with list sizeL=8 are used at the destination node.

Figure 2 depicts the BLER performance of the proposed ADF relaying for AWGN channel.The channelWSDis physically degraded by 2dB compared to the channelWRD,while the channelWSRis physically degraded by 1dB compared to the channelWSD.The performance curves of SC decoders are marked by solid lines and those of SCL decoders are marked by dotted lines.The performance of the ORA-ADF with SC decoding is marked by maple curve.When channelWSRis degraded with respect to channelWSD,the proposed ADF relaying with SC/SCL decoder marked by the red curves performs better than SC/SCL decoding(marked by black curves).Thus,it is verified that the proposed ADF relaying is available when channelWSRis degraded to channelWSD.On the contrary,the conventional DF relaying schemes such as the smart DF (SDF) relaying in [13] performs worse than normal SC decoding that without the help of the relay node.When channelWSRis degraded to the channelWSD,transmit all of the information bits at the relay node could cause unacceptable decoding errors.Thus,conventional DF relaying schemes are usually reliable when the channelWSRis upgraded to the channelWSD.The DF relaying in[14]requires a very long block length to achieve full theoretical rates.Thus it does not perform as well as the proposed ADF relaying for short or medium block length.The ORAADF is slightly better than the proposed ADF relaying with SC decoding(marked by the red curve)since that in ORA-ADF,the relay node and the destination node always know that whether the received messages are correctly decoded.The performance difference between the ORA-ADF and the proposed ADF is negligible.Thus,it is reasonable to apply the ORA-ADF model to simplify the analysis of the decoding performance and figure out the re-encoded bits number in the paper.

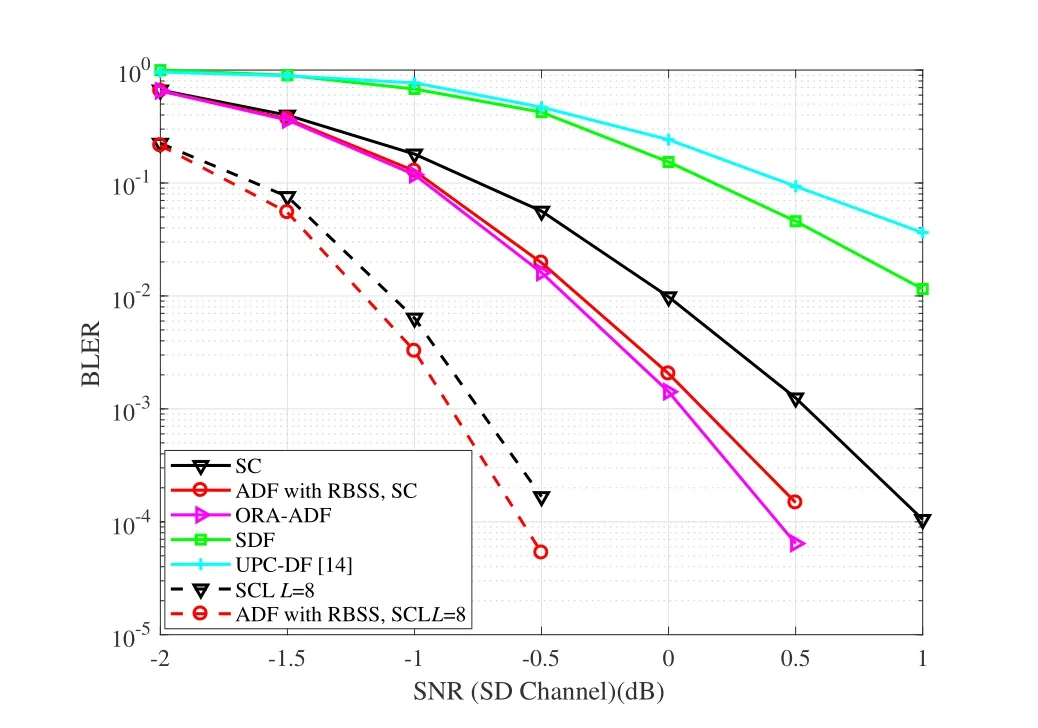
Figure 2.Performance comparison in AWGN channel with channel WSR degraded to channel WSD.

As shown in Figure 3,with channelWSDdegraded by 2dB to channelWSRandWRD,the ADF relaying outperforms the SDF relaying in[13]with SC decoder(marked by solid lines)or SCL decoder(marked by dotted lines).Furthermore,the ADF relaying with the relay re-encoded bits selection strategy (RBSS,marked by the red curves)achieves the similar performance as that with an exhaustive search to select the best re-encoded bit set.(marked by the blue curves).Thus,the proposed RBSS reduces the computational complexity with a negligible performance loss.The ADF relaying with the RBSS achieves a similar performance as the ADF relaying without the strategy(marked by the black curve).In this case,the incorrect decoding in channelWSRis the dominant error event.Thus the relay re-encoded bits selection strategy aimed at reducing the errors in channelWRDhas a marginal effect.

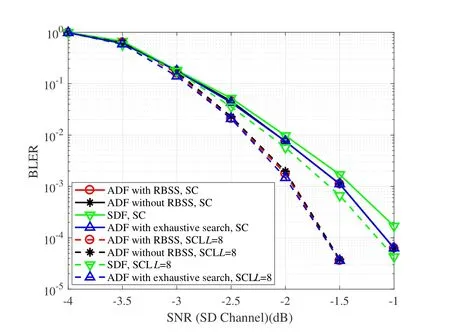
Figure 3.Performance comparison in AWGN channel with channel WSD degraded to channel WRD.

As shown in Figure 4,with channelWSDdegraded by 2dB to channelWSR,and channelWRDdegraded to channelWSDby 2dB,the ADF relaying with the relay re-encoded bits selection strategy (RBSS) outperforms the SDF relaying method in [13] and the ADF relaying without the strategy,and achieves similar performance as the ADF with an exhaustive search method for AWGN channel.Compared to the channel condition with a high reliability channelWRD,in this case,the incorrect decoding in channelWRDalso plays an important role.Thus,the relay re-encoded bits selection strategy aimed at reducing the errors in channelWRDefficiently reduces the overall decoding errors of the whole scheme.

Figure 4.Performance comparison in AWGN channel with channel WRD degraded to channel WSD.

TheKRdecided by RBSS in simulation results are provided in Table 1.WhileWRDis in a lower SNR regime,the relay re-encodes fewer bits to avoid introducing too many errors inWRDtransmission.ForWRDin a higher SNR regime,more bits can be reencoded and transmitted with guaranteed decoding performance.

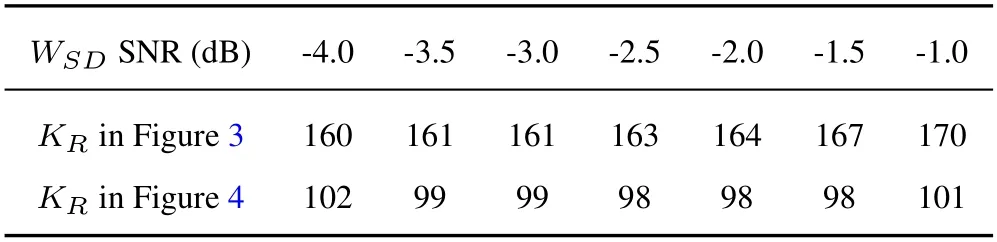
Table 1.KR decided by RBSS in simulations.

In Figure 5,simulation results with differentKRvalues are provided.Since the relay re-encoded bits selection strategy is mainly aimed at reducing the errors in channelWRDand is efficient when channelWRDwithout an ideal channel condition,we pick the channel conditions as channelWSDdegraded by 2dB to channelWSR,and channelWRDdegraded to channelWSDby 2dB.As shown in Figure 5,the ADF applied proposed re-encoded bit selection strategy(marked by red curves)outperforms improperKRvalues,such asKR=0.75K,KR=0.25KorKR=0.5K(marked by blue,maple and black curves respectively).Intuitively,an improperly highKRvalue causes high decoding error probability over channelWRD.On the contrary,an improperly lowKRvalue causes the relay re-encoded word carries few information and provides limited help to the decoding of the source information at the destination node.

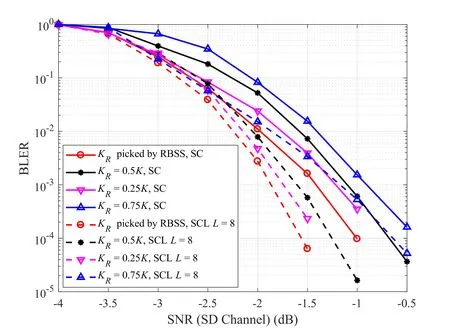
Figure 5.Performance comparison in AWGN channel with channel WRD degraded to channel WSD.

For the RFC,the proposed method can also be applied and the conclusions are consistent.As shown in Figure 6,with channelWSDdegraded by 2dB to channelWSR,and channelWRDdegraded to channelWSDby 2dB,the ADF relaying with the relay re-encoded bits selection strategy (RBSS) outperforms the SDF relaying method in[13]and the ADF relaying without the strategy,and achieves similar performance as the ADF with an exhaustive search method for RFC.

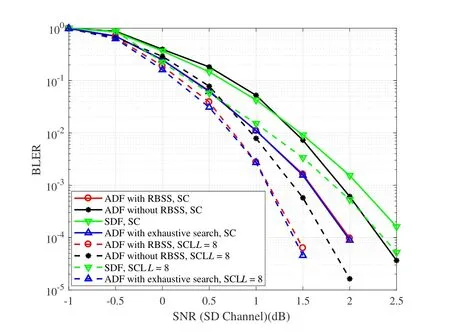
Figure 6.Performance comparison in RFC with channel WRD degraded to channel WSD.

VI.CONCLUSION

In this letter,we propose an arbitrary decode-forward single-relay scheme for finite blocklength polar codes.Based on the estimation of the decoding error probability,we propose a selection strategy to decide the proper set of bits to be re-encoded and transmitted by the relay.Simulation results verify the efficiency of the proposed designs for both the AWGN channel and the RFC.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China under Grant 92067202,Grant 62071058.