Predictive Tracking Implementation for Mobile Communication Using Programmable Metasurface

Yueheng Li ,Sven Bettinga ,Lucas Giroto de Oliveira ,Mohamad Basim Alabd ,Joerg Eisenbeis ,Xiang Wan ,Xueyun Long,Tiejun Cui,Thomas Zwick

1 Institute of Radio Frequency Engineering and Electronics(IHE),Karlsruhe Institute of Technology,Karlsruhe 76131,Germany

2 Southeast University,Nanjing 211100,China

Abstract: The programmable metasurface(PM)is an antenna array architecture that realizes flexible beam steering.This functionality is achieved by controlling the unit cells designed with micro components such as positive-intrinsic-negative (PIN) diodes,which offers potential cost reductions in the next generation wireless communication systems.Although PM has been a popular topic in antenna design,its implementations in real-time systems accompanied by signal processing algorithms are challenging.In this paper,novel predictive tracking algorithms for mobile communication scenarios using a PM are created and implemented in a real-time system operating at 28 GHz.An angular speed prediction(ASP)algorithm is proposed to compute the position of user equipment(UE)based on the previously recorded beam directions.As another solution,an angle correction (AC) algorithm is proposed to further improve the prediction and tracking accuracy.As a benchmark,the comparisons to a previous PM tracking algorithm without prediction are presented.Both simulation and measurement results show that the prediction algorithms successfully improve the tracking performance,which also prove the feasibilities of PM-based systems to solve complex real-time signal processing problems.

Keywords: signal processing;mobile communication;antenna arrays

I.INTRODUCTION

Since the beginning of the 21st century,mobile communication generations have been developed rapidly.To satisfy the demands of massive data traffic,wider bandwidths are required than ever before.As a solution,the 3rd generation partnership project new radio (3GPP NR) standards [1] have licensed the fifthgeneration (5G) wireless bands close to millimeterwave frequencies,for example,the NR band n261 from 27.5 to 28.35 GHz.However,signal propagations at higher frequencies suffer from stronger free space path loss (FSPL).To maintain a sufficient received signal quality,one solution is to implement small cell mobile access scenarios with base stations(BSs) serving user equipment (UE) in smaller coverage areas [2].Another solution would be the utilization of large-scale antenna arrays which validates beamforming technologies to concentrate power towards desired direction of departure/arrival (DoD/-DoA).Both of the aforementioned solutions lead to higher hardware efforts.Thus,for mobile and wireless communication networks,technologies that reduce the system costs and power consumptions guarantee great commercial benefits.From the antenna design point of view,an architecture called programmable metasurface (PM),has been studied in [3] as an antenna array candidate in wireless communication scenarios.The steerable beamforming can be realized by electronically controlling the states of the unit cells designed with cheap micro components such as positiveintrinsic-negative(PIN) diodes.In[4–9],the PM has been utilized in communication systems to prove its beamforming functionalities.For the most recent publications,PMs are taken into consideration as a part of the signal processing algorithms.In [10],the PM is implemented to achieve phase shift keying modulation schemes.Furthermore,the time division multiple access has been implemented into the PM-supported wireless communication systems in [11,12].The space and frequency division multiplexing has been realized by PM in [13].The multiple input multiple output(MIMO)functionalities are achieved using dual polarized PM as presented in[14].These studies build up a solid fundamental of experimental PM research.

Beamforming technologies realized by PM and other antenna array architectures enhance the received power but narrow the coverage width.Therefore,besides the aforementioned studies,ensuring the alignment of beam direction with the UE in mobile communication scenarios using PM becomes a necessary task.For UE tracking algorithms,literatures can be found at lower frequencies in[15,16].These articles have shown that the localization resolution benefits from rich scattering due to multiple reflection paths.However,such algorithms are not directly applicable to the systems operating at millimeter-wave frequencies,since sufficient rich-scattering is hard to be maintained due to the stronger FSPL.So far,studies regarding 5G tracking systems at 28 GHz have been demonstrated in [17–20] based on the 3GPP 5G NR beam training standards[21].Fruitful results have been delivered by utilizing conventional MIMO or phased array architectures.However,these architectures suffer from higher costs in comparison to the PM.Therefore,in[22]the authors firstly presented a tracking system utilizing the PM from[23]by adapting 3GPP 5G NR standards to exhaustive beam training refinements.In this paper,such system will be further improved and studied with the contributions listed as follows:

• Novel predictive PM tracking algorithms are created and analyzed.The angular speed prediction(ASP) algorithm realizes a prediction based on the computation of the angular speed using the measured beam direction as reliable benchmark.The angle correction(AC)algorithm improves the prediction preciseness of the ASP counterpart by implementing an angle correction according to the local power maximum.Comparisons to previous tracking systems are analyzed to show the features and improvements.

• Although PM is a popular topic in recent years,its functionalities are mostly at the proof of concept stages.Therefore,the proposed algorithms in this paper consider PM beamforming constraints to ensure their experimental possibilities.As the first system using PM predictive tracking,measurement results gathered from the real-time system match the theoretical expectations.This is an important milestone to examine the feasibilities of PM to perform complex beamforming tasks,which were rarely discussed before.

• Comparable results are delivered to the existing phased array or MIMO tracking systems in training time and the number of beam candidates.The results prove the potential commercial benefits of low-cost PM systems with proper performance.

The paper is organized as follows.In Section II,the beamforming basics of PM will be introduced to support the tracking algorithms descriptions in Section III.The system setup is stated in Section IV.The simulation and measurement results are analyzed in Section V.In the end,we conclude the paper by Section VI.

II.PM BEAMFORMING PROPERTIES

In this section,the influence of PM beamforming on the received power in the context of the proposed channel and propagation model is introduced.The practical PM beamforming constraints are further discussed to verify the necessity of adaptive PM tracking algorithms.

2.1 PM Beamforming Basics

A PM is a type of reflect-array consisting of electronically controllable unit cells,that are illuminated by a feed antenna.The beam direction is thereby controlled by the phase distribution of the unit cells.According to [22,24],the desired PM beam direction is defined withφ′andθ′,whereφ′is the azimuth axis of the PM plane,andθ′is the elevation axis.This leads to

withmandnto be the two-dimension unit cell indexes with the uniform spacing between unit cells asD.The termκ=is the wave number withλto be the wavelength at the carrier frequency.The variableψ′(m,n)represents the additive phase shift due to the distances between the phase center of the feeding antenna to the unit cells on the PM.In this condition,the simplified far-field pattern for the PM beamforming can be expressed as

Based on [25],assuming a lossless condition,the antenna gain of the PM is expressed as

In this paper,a line-of-sight (LoS) path is assumed to exist between transmitter and receiver.Due to the high FSPL and the low power leakage by the sidelobes of PM beamforming[22,23],the scattering caused by reflections only leads to weak interference which is neglected for the received power consideration.Therefore,the received power for the UE at positionθr,φrwith the beam directed towardsθ′,φ′after the free space propagation is

2.2 Practical PM Beamforming

So far,the signal model is only considering an optimum situation.In practice,the phase resolution of the PM unit cells should be considered.As stated in[3,23] and other existing PM literature,the mostly used PM structure is realized by a single PIN diode on each unit cell,which yielding a 1-bit phase resolution.This cheap architecture highlights the costeffectiveness of the PM,while still providing very good beamforming capabilities.Therefore,the quantized PM phase distribution assuming 1-bit phase resolution can be described as

By replacing the quantizedψqfrom(5)to the optimumψin(2),the realized PM beamforming contains quantization error for each unit cell.This leads to the fact that not all the beam directions can be reached with infinite angular resolution.On the other hand,a practical PM based on printed circuit boards suffers from side effects such as dispersion,inter-element coupling,etc.These effects may influence the quality of beamforming,which needs to be verified.Defining the tracking only alongθ′axis in this paper,a codebook for all the desired beamforming patterns can be generated by examining the set withφ′=0◦andinto(5).Here,gis the beamforming angular resolution from the start angleto the end angle.Figure 1 shows some beamfor candidates for our PM with the maximum achievable angular resolutiong=2◦.According to these observations,the PM achieves an accurate and uniform coverage over the area of interest,which is considered acceptable to realize proper beam tracking.

Figure 1.Measurement results of PM beamforming patterns with 2◦angular resolution along θ′ axis from −10◦to 10◦.

III.BEAM MANAGEMENT

In this section,the different PM tracking algorithms are introduced in detail.The general goal of a beam tracking system is to direct the beam to the optimum path between the transmitter and receiver.In practice,due to the quantization error from(5),the beamforming angular resolution from Figure 1,and the real-time signal processing latency,PM tracking cannot continuously achieve perfect beam alignment to a moving target.Therefore,algorithms are required to achieve the beam alignment as precise as possible during the entire tracking duration.This methodology is known as beam management[21].In general,a performance metric of the system is observed as a reference,for example,the received power.The received power at the UEP(θr,φr,θ′,φ′) is being observed while the PM phase distribution is set to beψq(m,n,θ′,φ′),withθr,φrdescribing the actual relative azimuth and elevation angle of the UE from the BS point of view.Sinceφ′=0◦is considered,P(θr,φr,θ′,φ′)is simplified to beP(θr,θ′).Then,a threshold needs to be defined as the minimum acceptable performance of the system.Once the performance metric falls below the threshold,beam refinement is triggered to update the beam direction to overcome the misalignment caused by the UE movement.This method is operated iteratively until the end of tracking duration[22].

3.1 Angular Speed Prediction (ASP) Algorithm

The first algorithm introduced in this paper is called angular speed prediction(ASP).Its detailed introduction is given in the following sections.

3.1.1 Predictive Tracking

The aforementioned beam management has been investigated in[22],as the first PM tracking system approach.However,there are two possible aspects can be studied to improve the system performance.Firstly,each beam refinement in [22] is accompanied by a beam refinement scan,which selects the best beam from a reduced set of beam candidates with respect to the chosen performance parameter.This leads to training overhead,as scanning might not always be necessary if sufficient knowledge about the UE movement is available.Secondly,as mentioned in[22],the system suffers from failures when the beam refinement scans are triggered too often,which requires a renewed initialization to re-define the UE position.Overall,the key to the solution is trying to avoid beam refinement scans as much as possible.If algorithms with predictive features can be employed,and realize beam alignments based on the predicted UE position,the training overhead caused by the beam refinement scans are expected to be reduced.

3.1.2 Main ASP Algorithm

The ASP algorithm is defined in Algorithm 2,which also shows how predictive tracking is applied to the proposed system.Since only one-dimensional tracking is performed.The variabletis defined as the time flow for the tracking algorithm.To initialize the system,a exhaustive full scan takes place in order to localize the initial UE positionbased on the peak received power,which consumes a time duration oftf.The counterscfandcrrecord the number of full scans and refinement scans for later performance analysis.Instantly,the selected beam direction is recorded with a time stamp and added to the beam tracking history as[1]=andT[1]=t,respectively.The reference powerPBfis noted after the scan based on the newly selected beam,and the observation through timetstarts with a predefined thresholdσ.The termPBfchanges for every observation stage to make sure that the current beamforming only depends on the most updated reference power,which makes the proposed algorithm suitable for flexible power levels.The beam directionis maintained until the received power drops belowσ·PBfdue to UE movement.During the observation stage,the reference powerPBfis also corrected upwards if the received power increases.This is designed for the reason that if the UE moves toward the BS with lower FSPL,the received power can be increasing even if the main beam is not properly aligned to the UE,which possibly worsens the system performance.As soon as the received powerP(θr,)[t] falls belowσ·PBf,a beam refinement scan is triggered within a narrow rangekconsuming a time oftr.By implementing another peak detection for the received power within the angle set,is updated and added to the tracking history in the form of[cr],T[cr].When there are more than one recordings in the tracking history list,which yieldsct=cf+cr >1,the angular speedvais estimated following(6)based on the two latest beam directions and time recording with indexesct −1 andct.Based on this angular speed,the angle prediction throughtis computed in (7).Once the current beam directionhas a mismatchof more than half of the angular resolutiongfrom the predicted DoD,beam steering is triggeredgdegrees towards the predicted direction[t],which is updated without heading to beam refinement scans.However,the beam refinement scans can be still initiated once the received power falls below the threshold to adjust the tracking,which normally means the prediction is no longer accurately following the UE movement.

3.2 Angle Correction(AC)Algorithm

The ASP algorithm described in the last subsections strongly relies on the accuracy of its beam scanning results.Hence,it cannot prevent the prediction from being gradually offset to the real UE position during the observation phase,as the PM only has a limited angular resolution that already impairs the initial speed estimate.Therefore,a fine tuning algorithm is required to increase the preciseness of the prediction.As a solution,we developed an angle correction (AC) algorithm which provides additional angle and timing information during the observation stage.Firstly,mathematical descriptions are presented to show the tracking condition and the spaces for further improvements considering PM constraints.Afterward,the AC algorithm is introduced in detail.

3.2.1 Angle Prediction Estimator Model

3.2.2 Statistical Considerations

First,we compute the expectation of our velocity estimate

whereby we made use of the following properties of the variance

(a) Var{a·X}=a2·Var{X}

(b) Var{X − Y}=Var{X}+Var{Y} −2 cov{X,Y}

(c) cov{X,Y}=0,if X and Y are statistically independent.

If we now regard the calculated variance as a measure for the scattering of the estimated speed values around their expectation,we can conclude that the scattering is inversely proportional to the square of time difference between two position measurements and directly proportional to the square of the angular resolution.In other words,shorter time intervals between two angle measurements will make the impact of the angle quantization error on the speed estimate much more severe if no additional measures are taken.In addition,due to the fixed angular resolution of the PM,this result fundamentally limits the ability of the system to correctly follow highly dynamic target movements with sufficient accuracy.Since we only employ a first order prediction model,the system has to deal with shorter beam refinement intervals in order to track dynamic targets,which in turn reduces the prediction accuracy and thus the ability to follow the target with optimum beam alignment.This directly motivates the need for an AC algorithm,that tries to compensate for the quantization errors by retrieving additional angle and timing information during the observation stage.

3.2.3 Main AC Algorithm

To derive the highest average received power for the PM tracking with limited angular resolution,any update of beam direction should be slightly ahead of the UE movement.As a consequence,the received power will firstly increase to the optimum beam direction for the ideal instant=θr,and then decrease again until the beam direction is adjusted.The AC algorithm aims to subsequently correct the quantization errors within the tracking history and keep its entries as close as possible to this instant of ideal beam alignment.Since the AC algorithm shares the same angle initialization and beam refinement stages as the ASP algorithm,we only focus on the observation and prediction stage in Algorithm 4.In addition to the ASP algorithm,a local maximumPmaxis recorded by observing the received power,and interpreted as a reliable reference for the optimum beam alignment.This information can be used to improve the position estimation and speed prediction,as it does not contain a spatial discretization error like the scan and gives access to the exact time of perfect alignment.Thus,it minimizes the error terms from(8),(9)and ultimately(10).For each tracking duration within an unchanged beamforming angle,the received powerP(θr,)is utilized not only for updating the reference power,but also for identifying local power maximum.The direct method to determine the local maximum can be realized by searching for the peak received power level and the time index through one entire tracking observation stage.However,this approach would add a lot of latency to the processing as the power could only be interpreted in retrospect,and the angle correction would require a significant amount of memory.Instead,we choose to constantly updatePmaxfor each time indext,similar to the floating threshold that controls the beam reallocation.Once>Pmaxholds,the algorithm regards the beam alignment as ideal and setsPmax=As long as the received power increases,this happens for every time step and thus shifts the entryT[ct]=tin the tracking history towards the actual time of optimum beam alignment,while resetting the angle predictionto the current beam direction.After the beam direction is updated satisfying≥g/2,Pmaxis set back to 0 and the angle correction algorithm starts over again.

The expected AC algorithm always observes a finite time interval between two steering operations.If the beam is aligned slightly ahead of the target movement,the target will move towards the center of the beam and the receive power will thus increase.When the target is perfectly aligned with the beam,the receive power reaches its maximum which we therefore want to detect and try to make use of with the AC algorithm.When the target is moving out of the beam again,the receive power will successively decrease until the beam is adjusted.In case the beam is aligned behind the target after,the received power will only be monotonically decreasing and the local maximum will be detected immediately at the start of the time interval under consideration.In this case,the angle correction will not be triggered and the system continues to operate with the ASP prediction,because it is impossible to deduce the time of perfect beam alignment with out having it occurred within the observation time.

IV.HARDWARE SETUP

In this section,the measurement setup that realizes the aforementioned tracking algorithms will be introduced.

4.1 Measurement Environment

Figure 2 shows the block diagram of the proposed 28 GHz PM beam steering system,with the system setting parameters listed in Table 1.The signal propagation starts with the host PC generating root-raisedcosine (RRC) filtered quadrature phase-shift keying(QPSK)symbols.The signal is fed into the softwaredefined radio (SDR) of type USRP X310 which realizes the signal conversion from baseband (BB) to the intermediate frequency(IF).The conversions between IF and radio frequency(RF)are realized by RF frontand and back-end modules.At the output of the RF front-end,a horn antenna illuminates the PM and the desired signal is propagated to the receiver via beamforming.The boresight of the horn antenna is thereby 45◦inclined in elevation,illuminating the PM slightly from below,with a distance of 150 mm between the phase center of the PM and the phase center of the antenna as in[23].This spatial setup is realized by a precisely printed holder.At the receiver side,the signal is recovered by a similar setup consisting of a mobile antenna,a RF back-end module and a receiver USRP.To avoid local oscillator (LO) offsets,both RF modules share the same LO input.In addition,a 10 MHz reference signal and pulse-per-second (PPS) clock is necessary for the synchronization between the transmitter and receiver USRPs.The required unit cell voltage levels for these beam candidates are controlled bya field-programmable gate array(FPGA),and are obtained from a pre-calculated codebook.The FPGA in turn receives beam steering commands from the host PC via a serial peripheral interface(SPI).As expressed in Figure 2,the PM transmitter serves as the BS at a fixed position,performing UE tracking and beam steering.The UE on the other hand is represented by a horn antenna moving along a mechanical trace with controllable speed.The vertical distance between the trace and the PM is 1.9 m,yielding a DoD range from 20◦to−25◦.The system is set in an indoor environment as shown in Figure 3.

Table 1.System setting parameters.

Table 2.Comparison for different tracking algorithms.

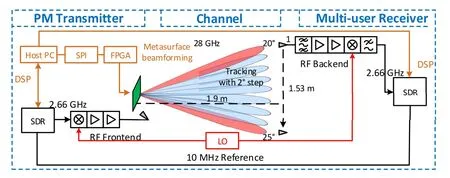
Figure 2.System model of a PM-based beam tracking system at 28 GHz.

Figure 3.Indoor system setup of PM mobile communication tracking based on[22].

4.2 Tracking Flow

To clarify the methodology of the proposed tracking algorithms,a flow graph is presented in Figure 4 to indicate the cooperation between PM and PC.Before tracking,the beamforming codebook of the FPGA has to be initialized based on(5)and the SPI beam steering commands from the host PC have to be defined.These host PC commands not only encompass fixed beam directions,but also more complex beamforming tasks like scanning over a range of beam candidates to simplify the interaction.Once the tracking starts,the target is initially localized by an exhaustive full scan initiated by the host PC.The PM has a fixed full scan duration which can be regarded as the start of beam selection for PC.Once the optimum beamforming angle is derived,a command to fix the beam direction is sent to PM and the observation of received power starts.Whenever the beam direction needs to be updated,either a refinement scan or a predictive update realized by Algorithm 2 or Algorithm 4 takes place.If no refinement scan is necessary,the system continuously loops the observation and beam management stages until the end of the tracking.

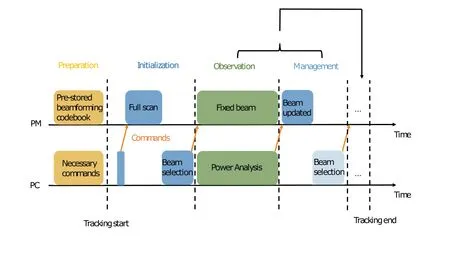
Figure 4.Flow graph for the tracking operation between PC and PM.

V.RESULT ANALYSIS

In this section,simulation and measurement results are analyzed to prove the feasibilities of the proposed tracking algorithms using the parameters mentioned in Table 1.These parameters are set in simulations to derive comparable results to the measured data.All the results are presented in Figure 5 with the simulation results from Figure 5a to 5c,and measurement results from Figure 5d to 5f.The time indexthas the resolution of 1µs which formulates the x axises of Figure 5.In these figures,blue curves denote the received powerand the yellow curves show the reference powerσ·PBf.For the simulation the power is a normalized value and for the measurement the power is measured at the input of receiver USRP.Each sudden drop of received power indicates one refinement scan.As a benchmark,the conventional algorithm in[22] is named as non-prediction (NP) algorithm for further analysis.

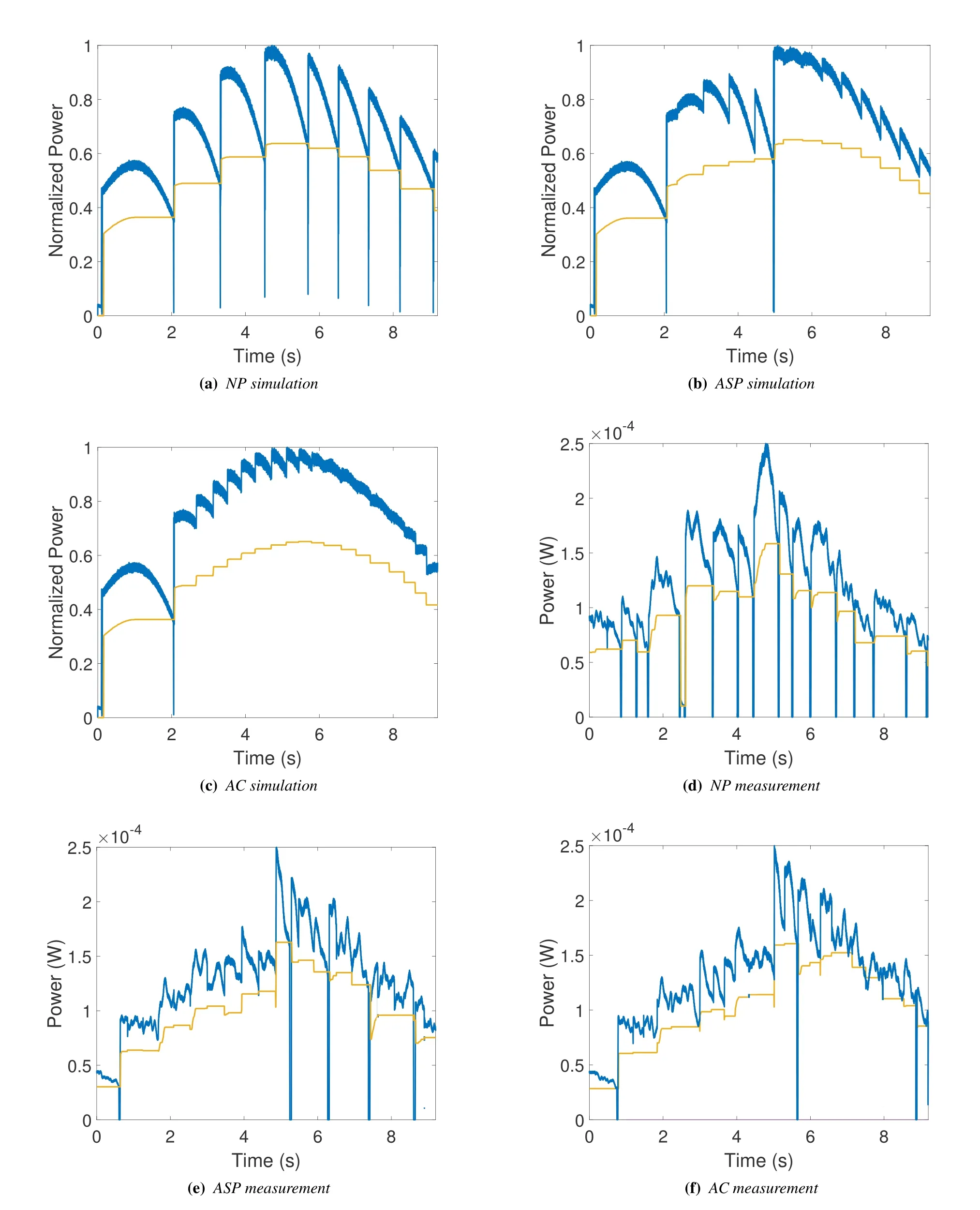
Figure 5.Figures for PM tracking system performance analysis.(a) to (c): Simulation results.(d) to (f): Measurement results.Blue curves denote the received power and yellow curves denote the tracking reference power.

5.1 Simulation Results

The results of NP algorithm are presented in Figure 5a,showing the highest number of refinement scans.In Figure 5b,the number of beam refinements is largely reduced by the ASP algorithm with with an exemplary refinement scan at around 5 s.At this moment,the reference power is reached and a refinement scan is triggered to search for reliable position information.Afterward,a sudden increase of power level can be seen,which means that the beam directions from the last angular resolutions were sub-optimum due to the prediction mismatch.The solution of this problem can be clearly observed in Figure 5c.With the help of the AC algorithm,there is only one necessary refinement scan at around 2 s that initialized the prediction.Afterward,the update of local maximum of the algorithm offers reliable UE speed and position estimation so that no further refinement scan is necessary.The aforementioned results prove that the implemented algorithms reduce the number of beam refinement successfully,which supports further experimental analysis.

5.2 Measurement Results

For each tracking algorithm,one example is depicted from Figure 5d to 5f focusing on the received power in blue and reference power in yellow.Starting with the NP algorithm,the most number of beam refinements can be observed.In Figure 5d,a typical failure can be observed for the beam refinement at approximately 2.5 s.In this case,the real-time computation loses track of the UE position,and has to carry out an exhaustive full scan to reacquire the target direction.The more beam refinements are operated over the entire tracking duration,the more such failures will occur statistically.This shows exactly why beam refinements times are aimed to be reduced in this paper.It can be clearly seen in Figure 5e that the number of beam refinement scans is largely reduced by the ASP algorithm.It also becomes evident that beam refinements are triggered more often during the UE movement away from the PM BS because the threshold levels are easier to be violated with fast power degradation.However,the threshold can not be reduced casually as this increases the probability of losing beam alignment with the target.This problem can be addressed using the AC algorithm in Figure 5f.With the angle correction using the constantly updated local maximum,the number of refinement scans becomes very low also when the UE moves away.However,due to noise and multi-path effects associated with the indoor environment,and the target movement contribution towards or away from the PM,there can be still mismatches which means the beam refinements can not be fully eliminated.Nevertheless,in comparison to the other two algorithms,the performance improvement is obvious.The functionalities of tracking reference power can be also clearly observed in Figure 5.Its level is softly set for each beamforming duration and changes based on the UE received power condition.This reference controls the beam training triggers,which validates the prediction algorithms with expected performances.Overall,both received power and reference power change as expected for all three algorithms.

5.3 Key Performance Parameters

To further analyze the performance of these tracking algorithms,we calculate the training overhead,average power,average angle mismatch,and average prediction mismatch as standards inspired by [22].The training overhead is defined to be the total training duration spent on beam scans over the entire tracking duration.The total training duration is expressed by

withtfandtrcan be further extended tots ·(()/g+1) andts ·(k/g+1),respectively.Here,tsis the time slot for each beam direction through the exhaustive search,andtdis the computation latency spent for the peak detection.In our system,tsis set to 0.3 ms andtdis measured to be 4 ms.The terms+1 and (k/g+1) denote the number of beamforming candidates in full scans and refinement scans.Afterward,by dividingTtrby the 9.18 s total tracking time,the training overhead is derived.To compute the averaged parameters,the total number of samples along timetis defined asNa.The average power is denoted by

To observe the angle parameters in this paper,the example corresponding to the AC algorithm measurement in Figure 5f is presented by Figure 6.The red line denotes the real position of the UE,while the blue curve shows how the PM beamforming changes its direction.The difference between the aforementioned curves expresses the angle mismatch given by the yellow curve.For tracking prediction,the purple curve shows the predicted angle and the difference to real UE position is the prediction mismatch sketched with the green curve.It can be observed that both prediction and beamforming have a small angle mismatch.When the angle initialization and beam refinements are triggered,the predicted angle and beam direction overlap with each other as expected.To mathematically analyze these parameters,the average angle mismatchAaand average prediction mismatchApare computed based on their differences with real UE position,which is expressed as

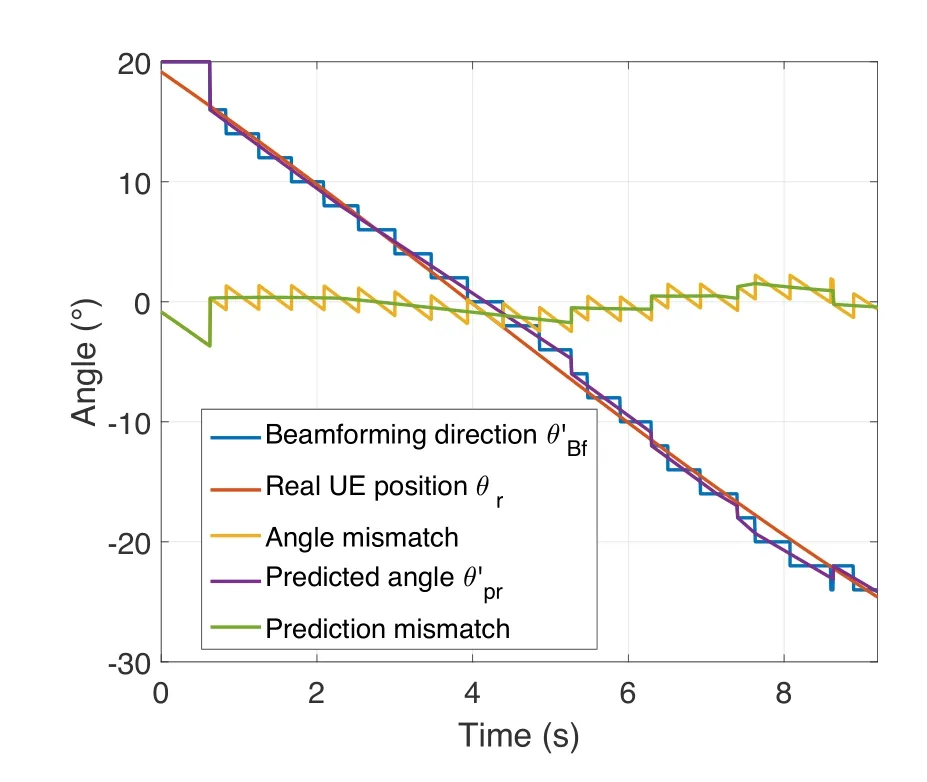
Figure 6.Angle analysis for AC algorithm corresponding to Figure 5f.

As mentioned in[22],the PM tracking system with NP algorithm outperforms former tracking systems due to its flexible training overhead which always keeps the redundancy as low as possible.In Table 3,we compare how the novel prediction algorithms further improved the system performance.The performance parameters are derived by averaging the values over several measurements.The training overhead is reduced around 3 times by ASP algorithm and further improved by AC same as the conclusion in Figure 5.This reduction is lower in comparison to simulation results in Figure 5d,due to the imperfect environment and measurements in practical of our proposed system and scenario.A higher average powerPacan be derived with lower training overhead since the data propagation during the beam refinement stage is not considered as effective power.Following the same logic,the angle mismatchAais improved by two aspects,especially when the system manages to perform all calculations and steer the beam towards target while the target is actually moving.Firstly,the latency caused by beam scans will introduce degradation of angle accuracy because during the scan and beam selection the beam aims at the sub-optimum direction.Secondly,with reduced number of beam refinements,failures are less likely to occur.The NP algorithm has no prediction mismatch since no prediction is operated.The prediction mismatch is lower in comparison to the practical angle mismatch due to the reason of limited angular resolution of the implemented PM as well as system latency.It can be concluded that the tracking ability is improved with increasing order by NP,ASP,and AC algorithm.The proposed new algorithms keep the beam refinement complexity at the level ofO{n}.As a trade-off,the system is required to observe the received power and compute the prediction information simultaneously.In comparison to theNP algorithm,ASP introduces the calculation of the speed estimate and the update of the tracking history after each scan.Furthermore the prediction of the UE angle and the subsequent comparison with the current beam direction has to be carried out for each observation time step.The memory to support a tracking history list is required and it has to be updated after every beam refinement scan.Upon that,AC introduces one comparison between the current power level and the maximum power per observation time step,as well as possibly an update of the maximum power level.When a local maximum is detected the history has to be updated.

Table 3.Comparison to tracking performances in other literatures.

Next,a further comparison including other tracking systems is shown in Table 1 and described as follows.The benchmark literature cover beamforming tracking measurements for variant wireless communication at 28 GHz for fair comparisons.Since the fastest angular speed of 37.5◦and the low angle mismatch is already presented in[22]and Table 2,we focus on the training overhead and the number of beam candidates in this paper.In the previous works,the algorithms are based on the implementation of certain number of time slots for tracking localization.It can be observed that in our work,after the implementation of AC algorithm,the training overhead maintains low even with the most number of beams in the codebook.The reason herefore is that many scans can be avoided by implementing prediction algorithms.In addition,the property of floating training overhead from[22]is maintained,which keeps the minimum amount of training time and high tracking accuracy in comparison with other works using a fixed amount of pre-assigned training slots being operated periodically over time.

5.4 Reproducibility Details

To provide reproducible measurements for further studies,the detailed equipment information and alternatives are given as follows.The implemented PM is controlled by an Altera Cyclone IV FPGA board with the core chip type EP4CE30F.This chip offers 400 general-purpose input-output (GPIO) pins that control the voltage levels to each unit cell of the PM.A codebook containing the phase distribution with the angle set is pre-stored in this FPGA and commands from the PC via SPI with type MCP2210 trigger the reconfigurable beam steering.To control the SDR and the SPI from Figure 2 simultaneously,out-of-tree modules supported by Gnu Radio Companion software are programmed using Python/C++.To support the real-time signal processing covering the 1 MHz bandwidth,10 G Ethernet cables have to be connected between the SDRs and the PC.In principle,different types of SDR or Radio Frequency System-on-Chip (RFSoC) can be implemented instead of USRP for signal generation and SPI commanding.If the computation ability outperforms the current system setup,the computation latencytdcan be further reduced which gains an even lower training overhead.For the implemented PM tested in [11],the maximum beam refresh rate of 0.04 ms is sufficient for the tracking system and the communication and settling time for beam steering is underµs range which is the reason why it was neglected.Any design of PM with proper beamforming ability and prompt responses can be an alternative.The RF frontend and backend modules are custom designs using low noise amplifier with the type HMC751LC4,power amplifier with the type HMC863ALC4,and mixer with the type HMC264LC3B[26].Other modules for conversion between IF and RF with sufficient noise figures will be also suitable.For the receiver side,the horn antenna is placed with a fixed orientation therefore the maximum power is reached in Figure 5 when the Rx horn antenna and PM are looking straight at each other.Since the algorithms consider flexible changes of power level,the problem of orientation angle can be solved.Nevertheless,different types of antennas operating at the correct frequency for the receiver can be also implemented.For changing the RF frequency of the system,some concerns have to be considered.For tracking and localization systems working at lower frequencies,more scatterings caused by reflection paths exist.This leads to more fluctuations of the received power which results in imperfect decisions of≥σ·PBfin the algorithms.As a result,the system may start the beam refinement or prediction earlier or later than the expected time point.To implement the proposed algorithms in these situations,a promising solution is to extend the observing duration.Instead of entering the beam refinement or prediction stage immediately when the threshold is triggered,more samples can be taken into recording.If a sufficient number of samples continuously hit the threshold in a period,this proves the sub-optimum of current beam direction and beam management should start.If in any case,a system has the ability to detect more precise channel state information using MIMO and multicarrier technologies,or offers other reference metrics such as error vector magnitude instead of received power,the proposed algorithms in this paper could be still applied.

VI.CONCLUSION

In this paper,a novel low-cost PM-based mobile communication system operating at 28 GHz is studied and developed.Novel prediction algorithms which consider PM-based system constraints improve the tracking performance of the system.Analysis based on simulation and measurement results has been performed and a good agreement between both has been observed.By implementing the novel tracking algorithms,the system performance is significantly improved.The achievements of this paper prove the ability of PM-based systems to perform complex beam management tasks even in real-time,which offers potential for future wireless communication technologies.