含初始缺陷海底管道侧向屈曲临界力的参数解

李 英，王 维，韩 宇

（1.天津大学 水利仿真与安全国家重点实验室，天津 300350；2.中海油能源发展股份有限公司采油服务分公司，天津 300452）

海底管道是世界油气运输的主要方式之一，管道内保持高温和高压的运行条件以加速碳氢化合物的流动防止凝固。受地基土体的约束，海底管道在温压联合作用及泊松效应下不能自由膨胀而产生轴向力，当轴向力大于管道临界屈曲荷载时，裸置于海床上的管道将发生侧向屈曲。不可控的侧向屈曲可能造成的严重后果，譬如油气泄露、强度破坏以及随之而来的疲劳失效等会对海洋环境、海底管道正常运行造成很大的影响。

基于理论分析和试验测试，Palmer 和Baldry［1］阐述了管道发生侧向屈曲的原因。Kerr［2-3］采用刚性平面的假设，建立了理想铁路轨道的侧向屈曲理论模型，并推导了前四阶屈曲模态的解析解。Hobbs［4-5］基于Kerr［2-3］对铁路轨道屈曲的研究，假设刚性海床具有恒定的摩擦阻力，推导得出了侧向屈曲临界荷载的解析解。Taylor 和Gan［6］、Taylor 和Tran［7］进行了一系列试验和解析解研究，提出了3 种初始缺陷模型和这3 种初始缺陷模型对应的临界载荷计算公式。基于理论分析和试验观察，Maltby 和Calladine［8］扩展了Hobbs［4-5］关于刚性海床上直管道的解析解，推导了临界屈曲载荷与海底管道初始缺陷的振幅、波长有关的无量纲参数解。基于量纲分析法，Zeng 等［9］将缺陷不平直度作为一个整体考虑，提出了新的垂向屈曲临界载荷公式，并给出了一个应用实例。基于缩比尺试验，陈志华等［10］通过热油模拟管道实际运行情况，研究了不同初始缺陷对管道垂向屈曲的影响。Wang等［11］提出了一种用于模拟含缺陷海底管道分布浮力模块触发侧向屈曲的分析模型，并通过试验数据进行验证，推导出了半解析解。Miles 和Calladine［12］基于小比例模型试验研究了含初始缺陷管道侧向屈曲问题，并提出了指数模型和双线性模型两种管土相互作用模型。基于动力显示分析方法，李成凤等［13］分析了土体约束力系数对长管和短管整体屈曲变形的影响。Wang 等［14］基于刚—塑性管土相互作用的假设，推导出了侧向屈曲临界力的解析解，与数值分析结果对比表明除预屈曲状态外，解析解与数值解具有极好的一致性。

上述研究成果为刚性或弹性海床上直管或某些含有初始缺陷管道的临界屈曲荷载估算奠定了基础。然而管土相互作用，管道初始几何缺陷以及自身材料特性对侧向屈曲临界力综合影响的明确函数表达式尚未被提出。因此分析了极限侧向土壤阻力、管道缺陷不平直度（缺陷波高与波长的比值）和管道截面几何尺寸对侧向屈曲临界力的影响。通过开展量纲分析，提出了一个包括这些相关参数的计算海底管道发生侧向屈曲所需临界屈曲荷载的一般表达式。

1 数值模型

1.1 管道模型

开展海底管道侧向屈曲研究的管道为X65钢，其几何与力学属性如表1所示。

表1 管道参数Tab.1 Pipeline parameters

应用ABAQUS 软件建立裸置海底管道侧向屈曲的数值分析模型。综合考虑管道的边界效应及计算效率，建立长度为2 000 m 的管道模型，中部通过Python 以脚本的形式导入初始几何缺陷，缺陷形态如式（1）所示。采用Pipe31划分管道单元，划分精度为1 m。

式中：Δ为初始缺陷的波高；L为缺陷的波长，取100 m；x则代表缺陷位置距离管道中点的距离。

为了研究管道材料非线性对侧向屈曲的影响，采用Ramberg-Osgood 本构关系［15］模拟管道钢材料的应力—应变关系，其中X65钢的应力—应变关系如图1所示。

图1 X65钢应力—应变关系Fig.1 The stress-strain relationship of X65 pipeline steel

1.2 侧向屈曲管土相互作用模型

采用非线性弹簧Spring1 模拟管土侧向与轴向相互作用。管土相互作用模型如图2 所示。考虑了土壤破裂的摩擦分量和被动阻力，横轴代表管道滑移距离，s表示管道位移突破值进行管土侧向分析时取0.1D，轴向分析时取0.01D或0.005 m［16］；纵轴代表突破临界力，其与管道淹没重量N的比值为摩擦系数μ（通常取0.2～0.8）［17］，临界力与突破位移的比值即为k。由于管道发生屈曲时的屈曲长度相较于整体长度而言较小，摩擦力对管道两端几乎没有任何影响，因此管道两端设为全约束。

图2 双线性管土相互作用模型Fig.2 Bilinear pipe-soil interaction model

1.3 数值方法

针对海底管道侧向屈曲的分析，在ABAQUS 中常采用3 种有限元计算方法，即静力、动力和Riks 算法［18］，三者各有优劣。静力算法使用增量牛顿法求解技术，但对于高度非线性问题，如侧向屈曲，使用静力算法容易出现不收敛的问题。之前的研究人员对这3种方法进行了比较［19-21］，发现这3种方法在预测峰值屈曲载荷方面非常一致。由于文中针对的是临界屈曲荷载的求解而不是屈曲后分析，因此动态解相对于Riks法［18］不会提供任何额外的优势。几何非线性静态问题有时发生跳跃形屈曲失稳现象，荷载—挠度响应显示为负刚度，结构必须释放应变能以保持平衡。Riks 法［18］使用载荷大小作为标量，允许确定完整的荷载—挠度曲线，包括荷载路径的反转。因此，为了分析屈曲前材料非线性和几何非线性有关的屈曲问题，采用Riks算法［18］。以50℃的变温荷载作为参考荷载，当屈曲发生时，“载荷比例因子—弧长”曲线出现拐点，以此求得侧向屈曲临界力。

1.4 数值模型验证

Taylor和Gan［6］对裸置于平坦海床上的管道进行了解析分析，并在分析过程中引入了初始缺陷。采用文献中的管道参数，利用有限元模型分别计算缺陷不平直度Δ/L为0.003、0.004和0.005的临界屈曲温度。表2给出了数值结果与解析结果的对比，结果表明两种方法计算的临界屈曲温度误差在8%以内，由此验证了所建立的数值模型的正确性和可行性。

表2 海底管道侧向屈曲在不同不平直度下临界屈曲温度Tab.2 Critical buckling temperatures of lateral buckling of submarine pipeline under different out⁃of⁃straightness

1.5 数值计算结果

基于上述管土相互作用模型，侧向摩擦系数与轴向摩擦系数均为0.6，针对缺陷幅值为0.25 m 的管道开展数值分析，得到的屈曲应力与管道变形如图3和图4所示。图3表明，管道的最大应力为148 MPa，发生在管道侧向位移最大的位置，图4表明最大位移为0.459 8 m。

图3 屈曲应力云图Fig.3 Buckling stress contour

图4 屈曲变形云图Fig.4 Buckling deformation contour

2 侧向屈曲参数分析

由于管道在制造和铺设等过程中产生的初始缺陷以及海床与管道之间的相互作用、管道自身的几何特性等都会对管道的侧向屈曲行为产生一定的影响［22-23］。因此，针对裸置于平坦海床上的管道进行有限元数值模拟，分析极限侧向土壤阻力、缺陷不平直度、管道截面几何尺寸等参数对管道侧向屈曲的影响。

2.1 极限侧向土壤阻力的影响分析

管土侧向相互作用采用双线性模型，在管道有效重度一定的情况下，侧向极限土壤阻力与侧向摩擦系数成正比。针对缺陷不平直度为1/400 的管道，不同侧向摩擦系数时管道轴向力—侧向位移关系如图5 所示。海床极限侧向阻力增大会导致海底管道临界屈曲轴向力增大；在该不平直度下，管道发生屈曲的过程都较为平缓，屈曲前后的轴向承载力并没有显著下降，所引发的后屈曲应力集中现象亦不明显。

图5 不同侧向摩擦系数下管道轴向力—位移曲线Fig.5 Axial force-displacement curve of pipeline under different lateral friction coefficients

为了分析临界侧向土壤阻力对临界屈曲轴向力的影响，图6 给出了不同侧向摩擦系数（μy= 0.2、0.4、0.8）条件下，管道不平直度Δ/L与临界屈曲轴向力的关系。由图6 可以看出，同一不平直度下临界屈曲轴向力随着侧向摩擦系数的增大而增大，表明侧向屈曲受到侧向极限土壤阻力的影响显著；随着侧向摩擦系数从0.8 降到0.2，不平直度为1/800 的管道，其临界屈曲轴向力从2.17 MN 减低到1.02 MN，而不平直度为1/100的管道，其临界屈曲轴向力从1.07 MN减低到0.72 MN。

图6 侧向摩擦系数对临界屈曲轴向力的影响Fig.6 Influence of lateral friction coefficient oncritical buckling axial force

2.2 初始缺陷不平直度的影响分析

海底管道在制造和铺设及运行过程中不可避免地会产生局部或整体初始几何缺陷。标准长度（12 m）的单根管道，初始缺陷不平直度通常小于1/500［24］。因此，综合考虑这种情况以及海床的不平直度，文中针对初始缺陷不平直度为1/800～1/100范围内的管道，开展初始缺陷不平直度对侧向屈曲的影响分析。

图7给出了不同不平直度的管道侧向位移与轴向力的关系。图7表明缺陷不平直度为1/100和1/200的管道，管道发生分岔型屈曲失稳，侧向屈曲前后管道轴向力并无明显变化；其他缺陷不平直度下的管道发生跳跃型屈曲失稳，屈曲后管道通过变形释放轴向力，并且轴向力下降的梯度随着不平直度的降低而变大。图8 给出了不平直度对临界屈曲轴向力的影响。随着不平直度的增加临界屈曲轴向力降低，并且两者呈现类似线性相关的关系，与不同摩擦系数时临界屈曲轴向力与不平直度的关系一致。

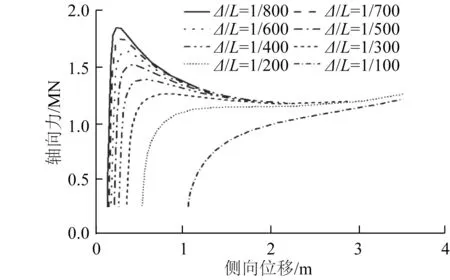
图7 不同不平直度管道侧向位移与轴向力的关系Fig.7 Relationship between the lateral displacement and the axial force of pipelines with different out-of-straightness

图8 不平直度对临界屈曲轴向力的影响Fig.8 Influence of out-of-straightness on critical buckling axial forces

图9显示了不同不平直度的管道在发生侧向屈曲时沿着管道长度方向的侧向位移。管道发生屈曲时屈曲的形式符合Hobbs第三阶侧向屈曲模态，并且变形最大处发生在初始缺陷中间位置。图10给出了管道初始缺陷不平直度对屈曲位移的影响。侧向屈曲发生时，屈曲位移随着不平直度的增加而增加，缺陷不平直度为1/100的管道，屈曲位移较不平直度为1/800的管道高了接近7倍。

图9 不同不平直度管道屈曲时沿管道长度方向的侧向位移Fig.9 Lateral displacement along pipelines with different out-ofstraightness during pipelines buckling

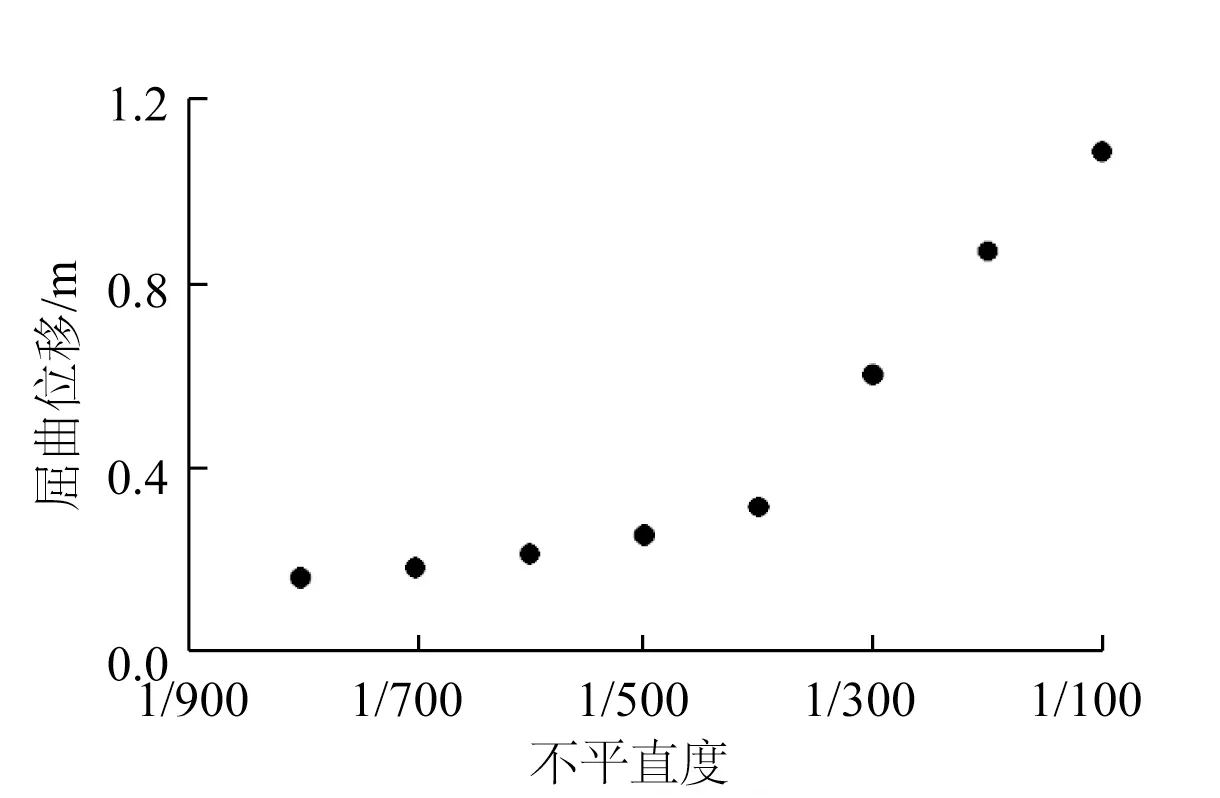
图10 不平直度对屈曲位移的影响Fig.10 Influence of out-of-straightness on buckling displacement

2.3 管道截面几何尺寸的影响分析

由于海底管道横截面几何尺寸对管道刚度有直接影响，因此，针对直径为323.9、457和650 mm，初始缺陷不平直度均为1/500 的3 种管道，通过改变壁厚来改变径厚比(D/t= 10、20、30、40、50)的方式研究管道截面几何尺寸对侧向屈曲的影响。

图11 给出了同直径管道在不同径厚比下，侧向位移与轴向力变化曲线。管道屈曲后通过变形的方式释放轴向力，并且随着径厚比的增加轴向力释放的过程愈加趋于平缓。

图11 D=457 mm管道不同径厚比下管道侧向位移—轴向力曲线Fig.11 Lateral displacement vs.axial force of pipelines with D=457 mm under different diameter-thickness ratios

图12 显示了3 种直径管道径厚比对临界屈曲温度的影响。相同直径的管道，径厚比越大临界屈曲温度越低；径厚比相同的管道，直径越大临界屈曲温度越高。这是由于截面积越大横截面刚度越大，管道的临界屈曲温度越高。图13 显示了相同直径管道，不同径厚比对临界屈曲轴向力的影响。随着径厚比的增大，管道临界屈曲轴向力降低。通过对比分析图12 和图13 可知，相同直径管道，径厚比D/t= 10 相较于D/t= 50，临界屈曲温度下降8.7%，临界屈曲轴向力下降46%。

图12 径厚比—临界屈曲温度曲线Fig.12 Relationship between diameter-to-thickness ratio vs.critical buckling temperature

3 侧向屈曲临界力公式

3.1 量纲分析

为了提出一个具有一般性的海底管道侧向屈曲表达式，基于量纲分析将管道侧向屈曲临界力表示为各种输入参数的函数。

根据欧拉屈曲理论和现有关于管道隆起屈曲的研究结果［23-24］，已知对于特定缺陷形状的管道，隆起屈曲的临界力仅与管道横截面刚度EI，管道水下单位重量q，以及缺陷的不平直度有关。考虑到文中研究的是侧向屈曲，因此，参考Maltby和Calladine［8］将上述q换为极限侧向土壤阻力F。表3总结了开展量纲分析时考虑的各种输入参数以及主要输出参数，即临界屈曲轴向力，共计4个输入变量，1个输出变量。

根据量纲分析的一般步骤［25］，先确定重复变量。根据表3给出的输入与输出参数的量纲，可知这个问题考虑的基本量纲为长度（L）和力（N），因此，选定缺陷波高Δ和管道横截面刚度EI为重复变量用于构造其他3个无量纲量，具体形式如式（2）所示。

将表3 中的量纲代入式（2），根据量纲齐次性原则，即可求得a1，a2，a3，b1，b2，b3，从而可以得到以下无量纲量：

量纲分析参考Maltby和Calladine［8］的屈曲解公式，用土壤的极限侧向阻力代替管道重量，给出了位于刚性（光滑）海底的直管屈曲临界载荷：

式（5）变形为：

另外，初始缺陷标称长度如式（7）所示：

式（7）变形可得：

在Maltby和Calladine［8］的分析中，由于对边界条件的设置，缺陷波长用侧向屈曲临界力与管道横截面刚度的函数形式表示，然而，一般数值模拟分析或试验中，缺陷波长作为一项独立的输入变量来考虑。因此，为了反映出缺陷波长L的影响，将式（6）右侧拆开，无量纲表达式转换为式（9）。

3.2 公式拟合

根据上述量纲分析得到的无量纲表达式式（9），可以得到拟合公式的一般形式：

两边取对数可变形为如下形式：

式（11）符合传统意义上的多元线性回归模型。因此，采用最小二乘法进行多元线性回归分析以求得参数a0、a1、a2。所采用的数据是通过使用一系列管道和管道—土壤参数（包括不同的Δ/L）对数百个独立响应的数值模型进行分析得出。数值模拟考虑的管道参数范围如表4所示。

运用Matlab 进行多元线性回归分析，得到的结果如表5和表6所示。对表5和表6所得结果进行显著性检验。首先进行拟合模型的整体显著性检验，所得的多重可决系数R2=0.997，其数值较大，检验得到的观测值F对应概率远小于显著性水平0.01，因此，拟合模型整体上来说高度线性相关；回归系数的显著性检验，截距、lnx1与lnx2所得检验观测值t对应概率P均远小于显著性水平0.01。因此，说明回归变量都对因变量影响显著。

表5 多元线性回归分析结果Tab.5 Multiple linear regression analysis results

表6 其他参数分析结果Tab.6 Other parametric analysis results

应用最小二乘法进行多元线性回归分析时，需满足一个最重要的假设性要求，即残差要满足正态分布的规律。因此，对拟合结果进行诊断分析，以检验其是否满足要求，提取拟合得到残差直方图与正态分布的重合曲线图，如图14和15所示。

图14 残差直方图Fig.14 Residuals histogram

图15 残差正态分布检验Fig.15 Residuals normal distribution test

由图14 和15 可以看出拟合模型基本符合最小二乘法的正态性假设，因此证明整个线性回归分析的正确性，从而得到海底管道侧向屈曲临界力的最终一般公式为：

3.3 拟合公式检验

为检验式（12）的拟合效果，分别开展管道在不同极限侧向土壤阻力、缺陷不平直度和管道截面尺寸下临界屈曲轴向力的拟合公式解与数值解的对比分析。图16给出了管道直径D=608 mm，不平直度为1/200情况下，不同侧向摩擦系数的管道数值计算与拟合的临界屈曲轴向力公式计算结果的对比关系，两者的最大相对误差为2.65%。图17 给出了管道直径D=608 mm，侧向摩擦系数为0.6 的情况下，不同不平直度的管道数值计算与拟合的临界屈曲轴向力公式计算结果的对比关系，两者的最大相对误差为 3.67%。图18给出了直径D=608 mm，侧向摩擦系数为0.6 的情况下，不同径厚比的管道数值计算与拟合的临界屈曲轴向力公式计算结果的对比关系，两者的最大相对误差为 1.83%。

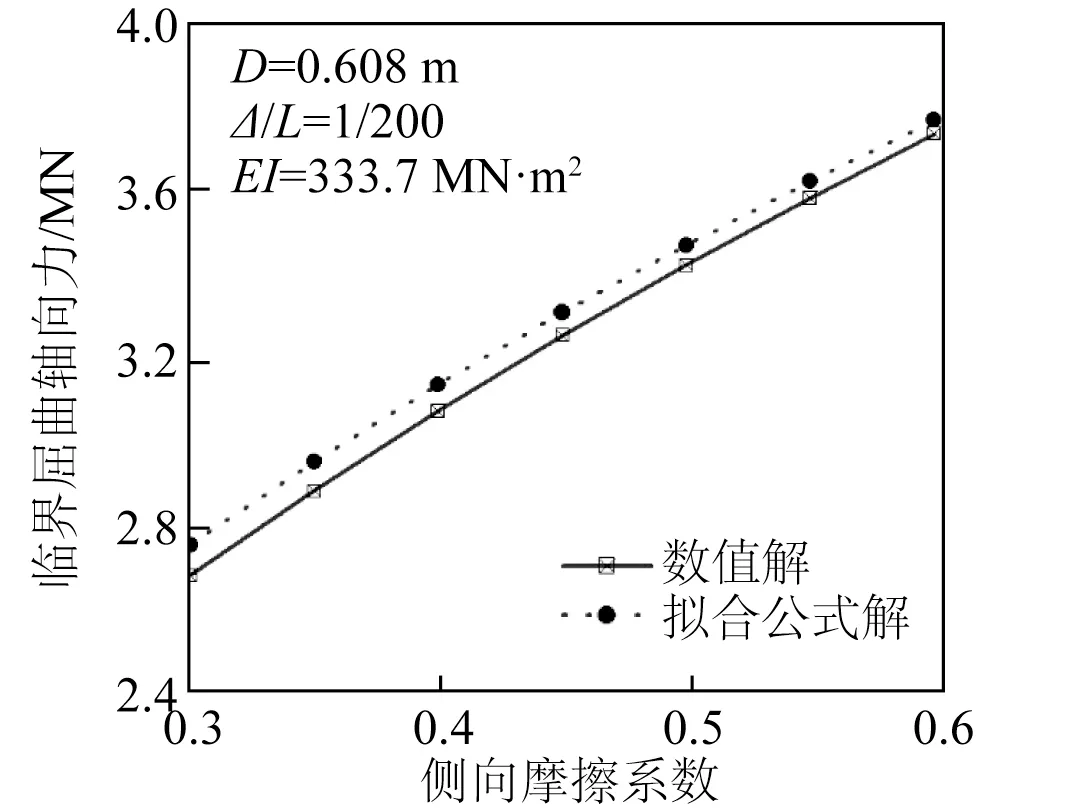
图16 不同极限侧向土壤阻力时数值结果与拟合结果对比Fig.16 Comparison of numerical results and fitting results for different limit lateral soil resistances

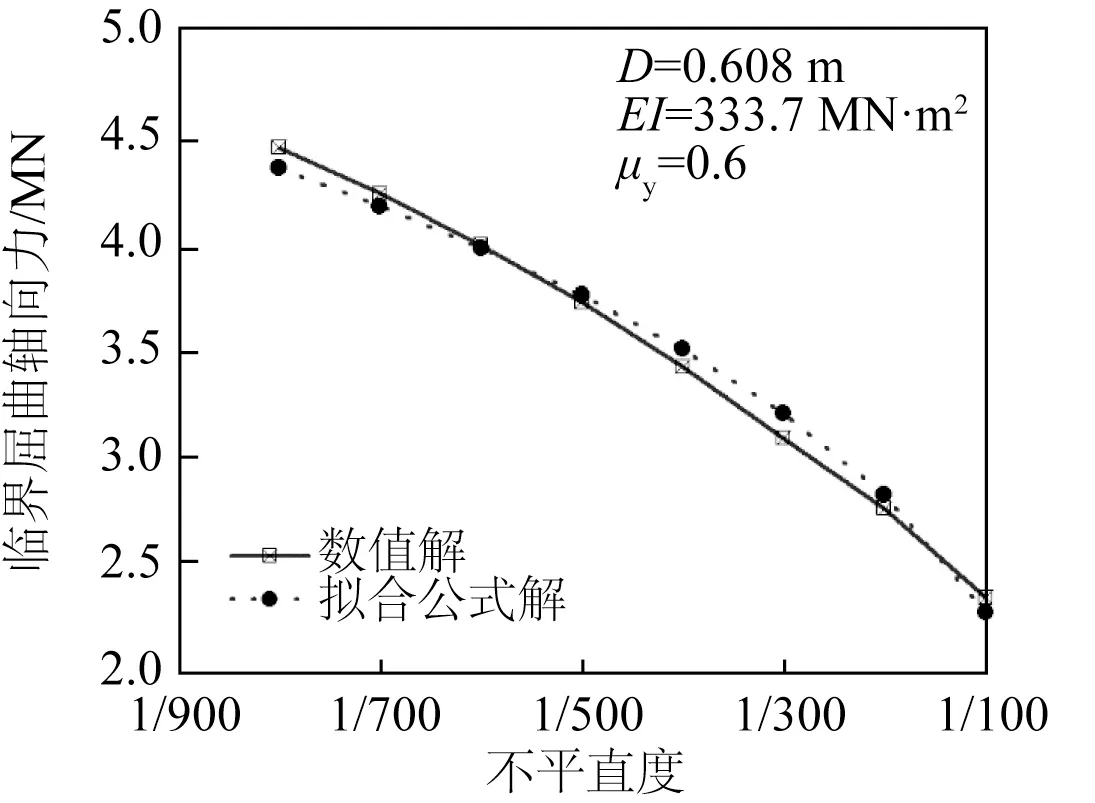
图17 不同不平直度的管道数值结果与拟合结果对比Fig.17 Comparison of numerical calculation and fitting results for different out-of-straightness pipelines

图18 不同截面尺寸的管道数值结果与拟合结果对比Fig.18 Comparison of numerical results and fitting results for different cross-section pipelines

综上，数值解与拟合公式解非常接近，最大相对误差为3.67%。由此表明由上述多元线性回归分析得到的临界屈曲轴向力一般表达式在参数研究涵盖范围内有效。

4 结 语

基于ABAQUS 有限元计算软件内置的Riks 算法，采用非线性弹簧模拟管土作用，对管道的侧向屈曲进行了数值模拟，并针对影响临界屈曲轴向力的管土侧向相互作用、管道缺陷不平直度、管道截面几何尺寸3个关键因素进行了参数分析。在量纲分析的基础上，结合数百组侧向屈曲数值模拟数据，采用多元线性回归分析得到侧向屈曲临界力的一般表达式。结论如下：

1）含有初始缺陷的海底管道，其初始缺陷的不平直度是影响海底管道侧向屈曲的重要因素。不平直度越大的管道临界屈曲轴向力越小，越容易发生屈曲；不平直度小于1/300 的管道可能会发生跳跃型屈曲，屈曲前后轴向承载力变弱，容易引发后屈曲应力集中现象。

2）极限侧向土壤阻力影响着临界屈曲轴向力，不平直度较小的管道受到的影响更显著，随着侧向摩擦系数从0.2增大到0.8，不平直度小于1/500的管道临界屈曲轴向力增幅超过50%。

3）管道的截面几何尺寸直接影响着横截面刚度，侧向屈曲临界力随着横截面刚度的增大而增大。

4）在量纲分析的基础上，基于非线性回归分析方法推导的侧向屈曲临界力一般计算公式，在参数研究涵盖的范围内能够很好用于海底管道侧向稳定性设计。