浸没式可移动外输终端系泊系统优化研究

2023-08-24陈国龙窦洪波张佳敏

海洋工程 2023年4期

李英，王坤，陈国龙，窦洪波，张佳敏

（1.天津大学水利仿真与安全国家重点实验室，天津 300350；2.中海油研究总院有限责任公司，北京100027）

我国边际油田较多，这些油田年产量小、开发年限短，且周围无可依托设施的油田，对“蜜蜂式”开发模式有一定需求［1］。“蜜蜂式”开发模式选择灵活且投资小的可移动采油设施对海上油田进行开发，可移动采油设施可以在多个油田重复利用，从而有效降低开发投资［2］。由于目前常用的CALM 系统受海域的气象条件影响较大，在台风或季风较大的海域，有效作业时间会相对减小，导致维护和运营成本增加。为了有效降低边际油田的开发投资，提出了一种新型外输系统用于边际油田的开采，此系统形式与CALM 系统类似，但为了减小我国南海恶劣环境对其外输终端的影响，外输终端浸没在水面以下并采用张紧式系泊系统。可移动外输终端桩基础采用吸力锚，在初始设计阶段，为了进一步降低成本，尝试将一组（两根）系泊缆系泊在同一个吸力锚上。如果此外输系统能成功应用于工程实际，将大大降低边际油田开发成本，对我国边际油田开发具有十分重要的意义。因此，文中对概念设计的浸没式可移动外输终端的系泊系统进行研究。

在系泊系统设计中，影响系泊系统安全的设计变量众多，如预张力的大小、导缆孔的位置、锚点的位置等。一个设计良好的系泊系统不仅可以降低系泊成本，还可以在满足自身强度要求的同时有效降低浮体的水平位移。因此，对系泊系统设计变量进行合理的优化具有十分重要的意义。郑纯亮［3］、辛露［4］、王莹［5］、马远［6］、张会良［7］采用人工试算方法对系泊系统进行了优化，但此种方法设计周期长，且所得结果并不一定是最优结果。智能算法发展迅速，可以用来对系泊系统进行快速优化。目前已有多位国内外学者应用智能算法对系泊系统进行了优化设计。早在2007年Shafieefar 和Rezvani［8］就提出了一种基于遗传算法的浮体系泊优化设计方法。Felix-Gonzalez 和Mercier［9］、孙丽萍等［10］也应用遗传算法对系泊系统进行了优化设计。Li等［11］提出了一种Kriging模型与基于梯度的搜索算法相集成的系泊系统优化方法。Giron等［12］提出了一种系泊系统和立管的集成设计方法，Monterio等［13］在Giron等［12］的基础上提出了一种基于粒子群算法的系泊系统优化方法。但上述学者仅考虑了浮体运动响应这一个优化目标，并未对系泊系统进行多目标优化。基于遗传算法，秦川［14］对CALM 系统的系泊系统进行了多目标设计优化，其利用加权法对两个目标函数进行归一化，将多目标优化问题转化成了单目标优化问题。Liang等［15］提出了一种NSGA-Ⅱ算法和船舶—系泊耦合模型相结合的系泊系统设计方法，建立了系泊系统设计的多目标优化问题。王颢然等［16］基于NSEA+算法，将传统锚泊定位分析方法和Optimus平台相结合，对某深海半潜式平台锚泊定位系统进行了多目标优化。

目前，针对系泊系统的优化设计研究主要集中在常规的浮体，浸没式浮体从设计到安装都面临着诸多新问题和新挑战，充分的优化设计至关重要。另外，系泊系统优化设计方法的适用性也需要通过对比分析来验证。文中以可移动外输终端最大水平位移及系泊缆最大张力最小为优化目标，以系泊系统结构安全为约束条件，分别应用第二代非支配排序遗传算法NSGA-Ⅱ和多目标粒子群算法对概念设计的浸没式可移动外输终端的系泊系统进行了优化，并对优化结果进行了对比分析。

1 可移动外输终端系泊系统时域耦合分析

1.1 可移动外输终端系泊系统参数及环境参数

概念设计的可移动外输终端由高1.5 m 的上部圆柱体与半径为4.5 m 的下部半球体组成，下部半球体球心距离水面14 m。其系泊缆布置采取3×2 的方式，各组系泊缆之间的间隔为120°。每组两根系泊缆间隔4°，且连接在同一个吸力锚上。可移动外输终端整体布置如图1 所示，正视图如图2 所示。表1 给出了其主尺度和具体计算参数。

表1 可移动外输终端参数Tab.1 Parameters of the submerged mobile offloading terminal

图1 系泊系统布置三维效果示意Fig.1 3D design skecth of the mooring system layout

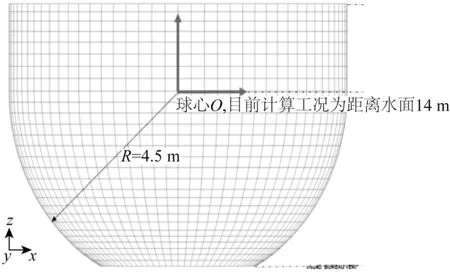
图2 可移动外输终端正视图Fig.2 Front view of the submerged mobile offloading terminal

系泊缆由锚链和钢缆两部分组成，其中，锚链端与可移动外输终端连接，导缆孔距可移动外输终端底部3.5 m，钢缆端与海底锚点连接，其各自主要参数见表2。

表2 系泊缆参数Tab.2 Parameters of the mooring lines

文中研究的可移动外输终端作业海域位于我国南海北部湾海域，设计水深40 m（相对于海图深度基准面），其坐标系定义如图3 所示，其百年一遇环境参数如表3 所示。所研究海域位于热带风暴地区，根据BV规范［17］，当波浪为主导海况时，要考虑0.5 倍的流速折减。这里通过线性插值确定了流速随水深的变化，结果如图4所示。

图3 坐标系定义Fig.3 Coordinate system definition

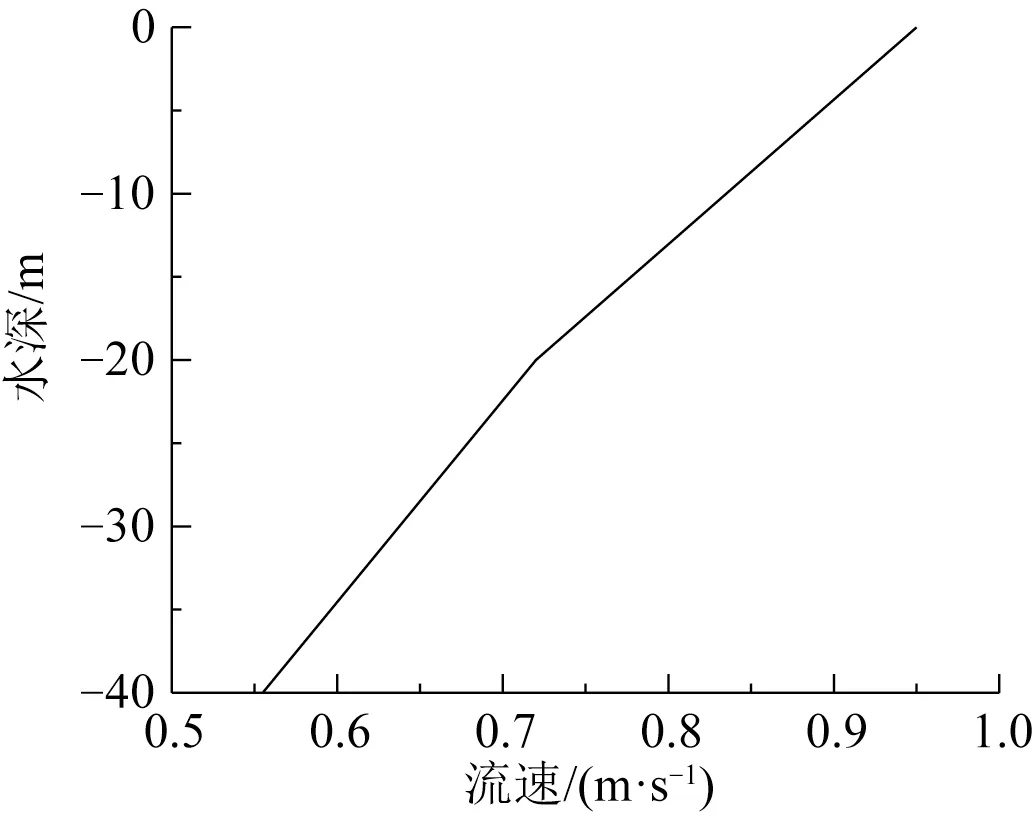
图4 流速随水深变化Fig.4 Variation of current velocity with water depth

1.2 可移动外输终端系泊系统时域耦合分析

在系泊系统数值分析中，常用的系泊系统分析方法主要有准静态非耦合时域分析法和动态时域耦合分析法两大类［18］。准静态非耦合分析法假定系泊系统静态地影响上部浮体的运动，仅提供回复力刚度，这种方法在每一个时刻根据计算上部浮体的位置确定系泊缆的形状，再用静力平衡的方法计算系泊缆的受力。动态耦合分析法将系泊系统和上部浮体整体考虑为动态系统联合求解，浮体运动分析中考虑系泊系统的阻尼和惯性效应，计算精度较高，相应的计算量也相对较大。准静态非耦合分析法计算方便快捷，但忽略了浮体波频运动对系泊系统的影响和系泊缆本身的动态效应，导致计算精度较差。由于浸没式浮体需要系泊系统上的张力保持静态平衡，浮体的波频运动受系泊缆影响较大，准静态非耦合分析方法不适用，所以采用动态时域耦合分析方法对系泊系统进行分析。

利用SESAM 对可移动外输终端进行了水动力分析。由于可移动外输终端浮力和重力不平衡且采用张紧式系泊系统，所以通过施加tether 单元来模拟可移动外输终端导缆孔处的初始预张力和各方向的系泊刚度，tether单元上施加的预张力237.8 kN，轴向刚度为6 375 kN/m。其水动力模型如图5所示。

图5 水动力分析模型Fig.5 Hydrodynamic analysis model

应用Orcaflex对可移动外输终端进行了时域耦合分析，其时域耦合动力分析模型如图6所示。因为可外输终端位于小尺度结构物到大尺度结构物的过渡范围，所以不能仅考虑依据势流理论计算出的非黏性波浪力，还需要考虑作用在可移动外输终端上的拖曳力。通过在可移动外输终端上施加莫里森单元的方法来模拟未包括的作用在可移动外输终端上的拖曳力。在系泊计算时，使用的黏性阻尼按照各自由度临界阻尼的10%进行取值，具体参数见表4。

表4 黏性阻尼取值Tab.4 Values of viscous damping

图6 时域耦合的动力分析模型Fig.6 Time domain coupled dynamic analysis model

选用JONSWAP 谱来模拟百年一遇的波浪，参数γ取1.45，模拟时长为3 h。由于波浪具有随机性，同样的波浪谱参数在不同波浪随机数工况下波浪力结果也存在差异，进而影响系泊缆最大张力和可移动外输终端最大水平位移。因此，依据BV规范［17］，针对同一海况选取5个波浪随机数进行数值模拟，最终结果由多次模拟结果的平均值和标准差定义。

在实际工程中系泊系统会受到来自各个方向的波流力，为了减小工作量和计算成本，在进行系泊系统优化设计时通常提取出响应最大的关键工况进行分析。根据经验和规范［19］，出于保守考虑，文中研究考虑波流同向。考虑可移动外输终端和系泊系统对称性，开展了入射角在0°～105°的范围内，间隔15°的波流方向工况分析。研究了波流入射方向对可移动外输终端最大水平位移和系泊缆最大张力的影响，结果如图7所示，此处的系泊缆指6根系泊缆中受力最大的缆，下同。

图7 波流方向敏感性分析Fig.7 Sensitivity analysis of wave and current direction

图7表明可移动外输终端最大水平位移和系泊缆最大张力都在波流方向为0°时最大。因此将波流方向为0°作为关键工况进行分析，文中的系泊系统参数敏感性分析及优化设计均是在此工况下进行的。

Study on the strategy of “separation” and “fusion” problem between new and old cities---A case study of Zhongshan Road in Qingdao City

2 系泊参数敏感性分析

为了确定系泊系统多目标优化设计变量，在一定范围内针对预张力大小、导缆孔位置等系泊参数开展敏感性分析，研究其对系泊系统性能的影响。表5给出了各系泊参数取值范围。其中，预张力的大小通过改变系泊缆中钢缆段的长度来调节，系泊缆总长等其他参数保持不变；改变锚链段长度时保证总长不变，钢缆段长度相应变化；改变导缆孔距可移动外输终端底部距离时，保持预张力不变，但系泊缆总长相应变化；系泊缆夹角发生变化时，系泊缆总长不变，锚点位置和预张力随夹角自然变化。

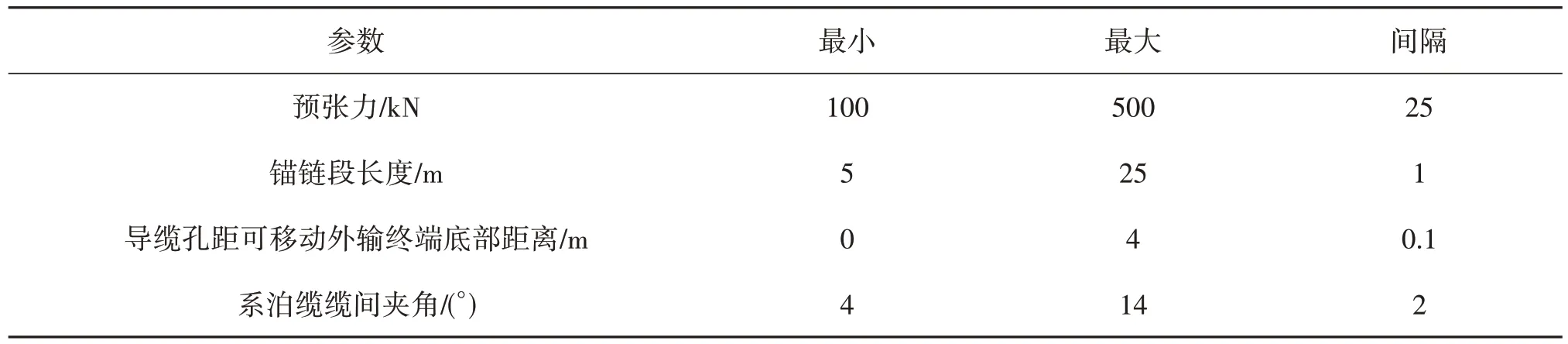
表5 系泊参数取值范围Tab.5 Value range of mooring parameters

图8给出了可移动外输终端最大水平位移和系泊缆最大张力与系泊缆缆间夹角的关系。图8表明随着系泊缆缆间夹角的增大，可移动外输终端的最大水平位移和系泊缆最大张力都逐渐减小。图9～11分别给出了预张力大小、锚链长度和导缆孔位置对可移动外输终端最大水平位移和系泊缆最大张力的影响。单独改变预张力大小、系泊缆中锚链段长度或导缆孔位置均无法满足可移动外输终端的最大水平位移及系泊缆最大张力最小。

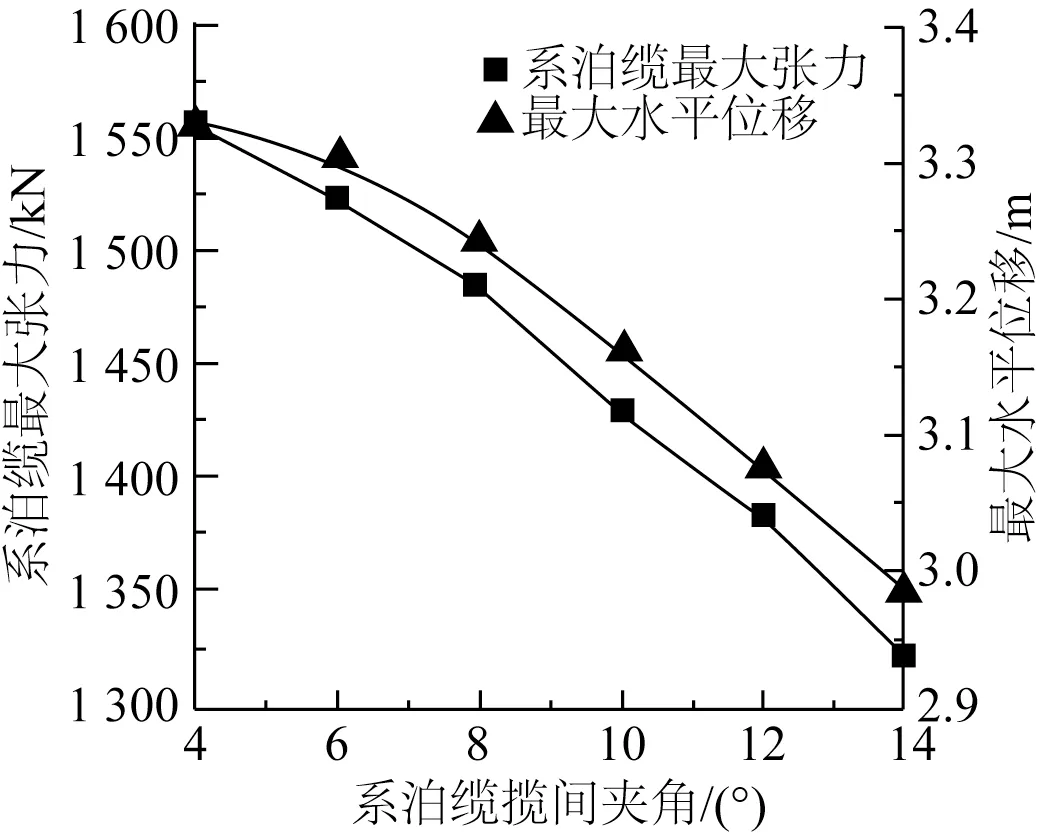
图8 系泊缆缆间夹角敏感性分析Fig.8 Sensitivity analysis of angle between mooring lines

图9 预张力大小敏感性分析Fig.9 Sensitivity analysis of pretension

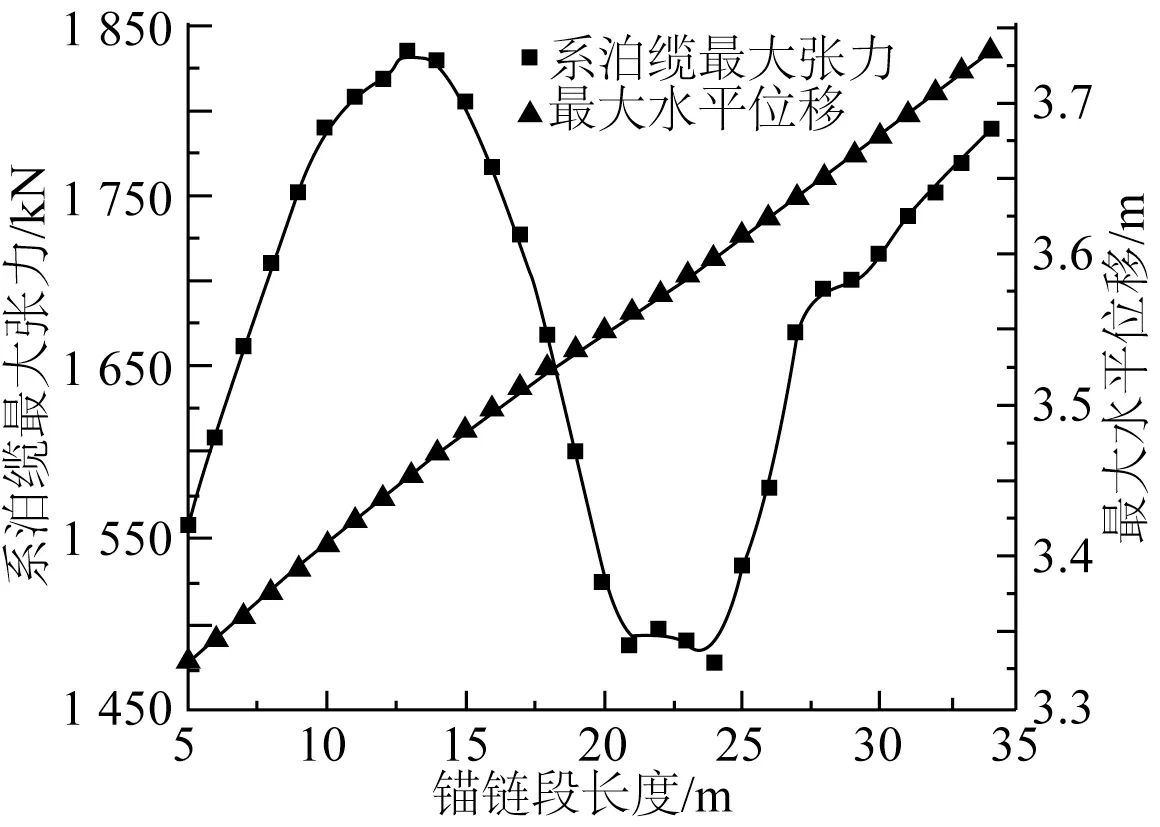
图10 锚链段长度敏感性分析Fig.10 Sensitivity analysis of the length of anchor chain segment

图11 导缆孔位置敏感性分析Fig.11 Sensitivity analysis of the location of fairleads

3 系泊系统优化设计

3.1 系泊系统多目标优化问题数学模型

BV 规范［17］中提出的锚泊设计衡准包括平台的水平偏移、系泊缆的张力、锚系统抓力和疲劳寿命等，其中最关键的是平台的水平偏移和系泊缆张力。系泊系统的主要作用是平衡作用在浮体的外力，为浮体提供回复力，减小浮体水平运动。系泊缆最大张力决定了系泊缆的等级，进而影响了系泊缆成本。因此，选取可移动外输终端的最大水平位移和系泊缆最大张力为优化目标。

系泊参数的敏感性分析表明预张力大小、系泊缆中锚链段长度、导缆孔位置、系泊缆缆间夹角都会对可移动外输终端的最大水平位移及系泊缆最大张力产生较大影响。由图8～11可知，只有当系泊缆缆间夹角这一变量增大时，系泊缆最大张力和外输终端最大水平位移同时减小，而当改变其他参数时，二者的变化趋势并不一致，即某个目标的改善可能导致其他目标性能的降低。由于系泊缆夹角超过6°后，若不改变初步设计选用的吸力锚直径和系泊半径，同一组系泊缆无法系泊在一个吸力锚上。基于此，综合考虑系泊功能需求及经济性，将系泊缆缆间夹角设为6°，将预张力大小、系泊缆中锚链段长度和导缆孔位置作为优化变量对系泊系统进行多目标优化设计，这3个设计变量间彼此相互独立。

由于系泊系统优化的目的是寻找比初步设计更优的系泊系统，因此将系泊缆最大张力小于1 800 kN，可移动外输终端最大水平位移小于4 m也作为系泊系统多目标优化问题的约束条件。系泊系统多目标优化问题的数学模型可以定义为：

式中：Pr为预张力大小，L为锚链段长度，Z为导缆孔距可移动外输终端底部距离，S为可移动外输终端最大水平位移，T为系泊缆最大张力。

3.2 基于NSGA⁃Ⅱ的系泊系统优化框架集成

采用NSGA-Ⅱ对系泊系统进行多目标优化设计，需集成NSGA-Ⅱ和系泊系统时域动力分析模型。Orcaflex 内含Matlab 等自动化编程软件接口，并能批量计算和提取结果，适用于解决系泊系统多目标优化问题。文中应用Matlab 编写NSGA-Ⅱ程序调用Orcaflex，构建系泊系统模型和开展时域动力分析，实现系泊系统多目标优化。整体优化框架如图12所示。

图12 基于NSGA-Ⅱ的系泊系统优化框架Fig.12 Optimization framework of the mooring system based on NSGA-II

优化过程如下：

1）基于NSGA-Ⅱ得到系泊系统优化变量值，通过Matlab 调用Orcaflex，根据得到的系泊系统优化变量值构建新的系泊系统模型。

2）在Orcaflex 中进行时域耦合动力分析，通过Matlab 提取可移动外输终端的最大水平位移及系泊缆最大张力，并将结果返回NSGA-Ⅱ。

3）NSGA-Ⅱ根据约束条件和适应度函数对结果进行选择和判断。

4）重复步骤1）～3）直至满足终止条件，即进化代数达到 40 代或连续3代种群内的个体全是 Pareto 最优解，输出Pareto最优解和系泊系统优化变量。

3.3 基于多目标粒子群算法的系泊系统优化框架集成

采用粒子群算法对系泊系统进行多目标优化设计需要解决两个问题，一是粒子群算法运行过程中找到的Pareto 最优解的保存，二是引导粒子飞行的个体最优粒子和全局最优粒子的确定。为了解决上述两个问题，参考Coello 等［20］的做法，在粒子群算法中引入外部档案的概念，并基于自适应网格法根据粒子拥挤程度在外部档案中确定全局最优粒子。基于上述算法，文中应用Matlab 调用Orcaflex，构建系泊系统模型和开展时域动力分析实现系泊系统多目标优化。其整体优化框架如图13所示。

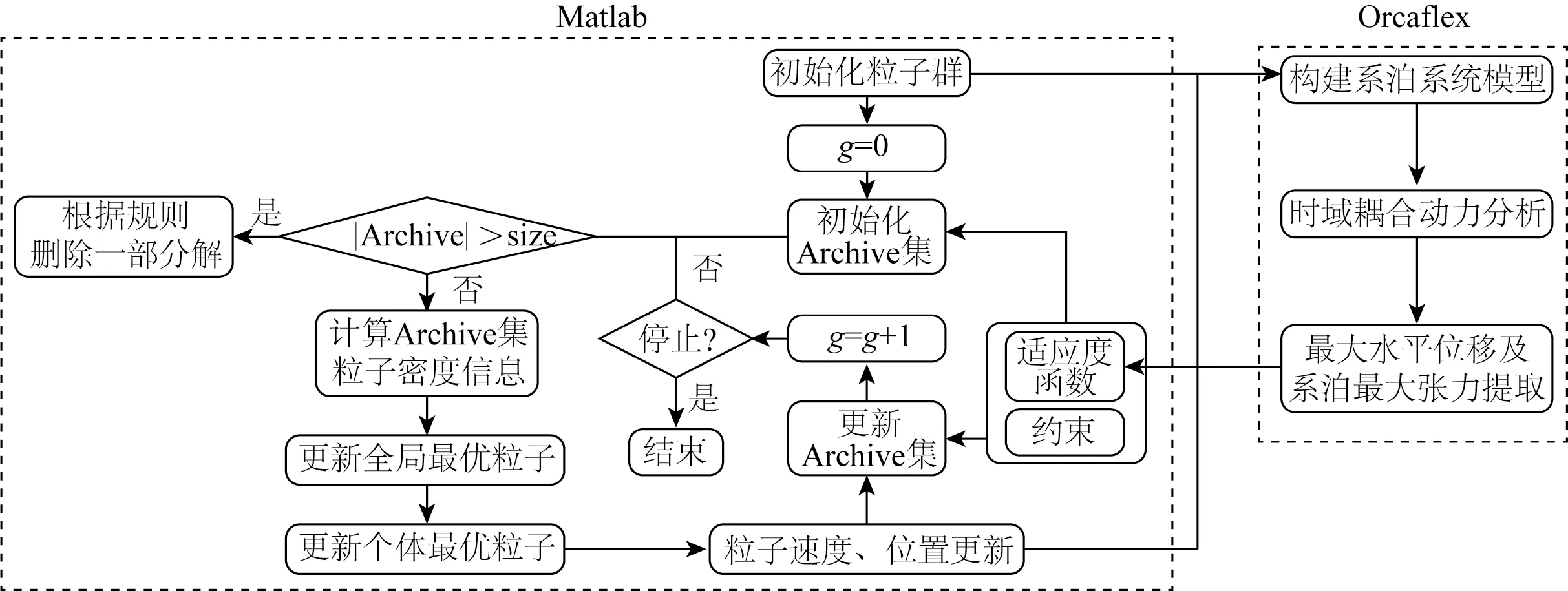
图13 基于多目标粒子群算法的系泊系统优化框架Fig.13 Optimization framework of the mooring system based on multi-objective particle swarm optimization

优化过程如下：

1）基于多目标粒子群算法得到系泊系统优化变量值，通过Matlab 调用Orcaflex，根据得到的系泊系统优化变量值构建新的系泊系统模型。

2）在Orcaflex 中进行时域耦合动力分析，通过Matlab 提取可移动外输终端的最大水平位移及系泊缆最大张力，并将结果返回多目标粒子群算法。

3）多目标粒子群算法根据约束条件和适应度函数对外部档案即Archive 集中的系泊系统优化变量值进行更新。

4）重复步骤1）～3）直至满足终止条件，即进化代数达到40 代或连续3 代外部档案内的Pareto 最优解数量超过其规定大小，输出Pareto最优解和系泊系统优化变量。

4 系泊系统优化设计结果分析

图14 给出了基于NSGA-Ⅱ和粒子群算法得到的系泊系统多目标优化Pareto 前沿，图中的每一个点都是Pareto 最优解，代表着一种系泊系统设计方案。图14 可以看出，相同系泊缆最大张力下，采用NSGA-Ⅱ算法进行优化得到的外输浮筒的最大水平位移较小，表明基于NSGA-Ⅱ得到的系泊系统多目标优化Pareto前沿优化效果更明显。在NSGA-Ⅱ中，染色体之间共享信息，种群分布较为均匀，得到50 个Pareto 最优解共进行了4 500 次计算。而粒子群算法整个搜索过程跟随当前找到的最优解，得到50 个Pareto 最优解只进行了2 400次计算。因此，用粒子群算法解决系泊系统优化问题比用NSGA-Ⅱ计算量更小，速度更快。

图14 系泊系统多目标优化Pareto前沿Fig.14 Pareto frontier of multi-objective optimization of the mooring system

综上所述，NSGA-Ⅱ和粒子群算法都能解决系泊系统多目标优化问题，但两者各有优缺点。粒子群算法原理简单运行速度快，NSGA-Ⅱ 迭代过程较为复杂导致运行较为耗时，但得到的Pareto 前沿优化性能更好。因此，针对系泊系统多目标优化问题，若更加关注优化性能的提高，NSGA-Ⅱ算法更具优势；若想在较短时间内达到不错的优化效果，则可以选择粒子群算法。因为这里更关注系泊系统的优化效果以在初步设计阶段获得性能最优的系泊系统，所以采用NSGA-Ⅱ解决浸没式可移动外输终端的系泊系统多目标优化问题。

实际工程中，系泊系统的设计需同时兼顾浮体最大水平位移和系泊缆最大张力这两个优化目标。系泊系统的预张力越大，锚端上拔力越大，对吸力锚的要求也越高，因此，在系泊系统能提供较好位移控制的情况下，选取预张力较小且位于Pareto前沿中间位置的方案为最优设计方案，确保对浮筒浮力需求较小并能有效控制浮体位移，具体如图14中的圆圈所示。

表6给出了系泊系统优化前和优化后的设计变量值。表6表明优化后的系泊系统导缆孔位置更靠近可移动外输终端底部，锚链段长度增加，预张力增大，更接近维持可移动外输终端静态平衡所需的系泊缆张力。

表6 系泊系统优化前后设计变量值Tab.6 Design variable values before and after mooring system optimization

系泊系统优化前后两个优化目标可移动外输终端最大水平位移和系泊缆最大张力值如表7 所示。表7表明，通过优化系泊系统可移动外输终端最大水平位移减小了31%，但系泊缆最大张力仅降低了3%。这是由于该可移动外输终端采用张紧式系泊，且完全系泊在水面下，其受到波浪作用时不能通过调节吃水来改变可移动外输终端所受浮力，系泊缆始终处于张紧—松弛状态，系泊缆张力容易出现较大的极值响应。因此，优化对可移动外输终端最大水平位移具有明显效果，对系泊缆最大张力效果不明显。