着眼于问题解决的小学数学“读思达”课堂教学模式探究
2023-08-24朱桂云

摘 要:培养学生核心素养已成为新时代基础教育的基本理念。余文森教授把握新时代特点,提出“读思达”教学法。阅读、思考、表达过程正是认知输入、认知加工和认知输出的过程。在此过程中,学生发现问题,提出问题,分析问题,解决问题,由此建构良好的数学认知,同时发展数学学科核心素养。文章以“探索活动:梯形的面积”为例,详细论述着眼于问题解决的小学数学“读思达”课堂教学模式和相关策略。
关键词:小学数学;问题解决;“读思达”课堂教学模式;教学策略
中图分类号:G427 文献标识码:A 文章编号:2097-1737(2023)20-0005-03
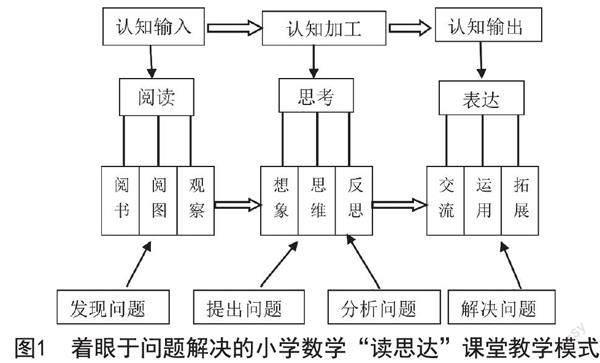
“核心素养究竟如何落地”“怎样培养学生的核心素养”是新时期迫切需要解决的教育问题。福建师范大学的余文森教授在《核心素养导向的课堂教学》一书中回答了这两个问题。他强调:阅读能力、思考能力和表达能力是构成核心素养的关键能力;阅读是一种接受式学习,思考是一种探究式学习,表达是一种讨论式学习;学生经历阅读、思考、表达,可以实现对核心素养的“完整学习”[1]。基于此,余文森教授总结出“读思达”教学法:阅读即认知输入,学生在认知输入阶段要阅读文字或图画,细心观察,发现问题;思考即认知加工,学生在认知加工阶段要积极想象、认真思维、自觉反思,由此提出问题、分析问题;表达即认知输出,学生在认知输出阶段要进行交流、运用、拓展,不断解决问题。鉴于此,教师应彰显教学智慧,归纳出着眼于问题解决的小学数学“读思达”课堂教学模式,具体如图1所示。
下面,笔者以北师大版小学数学五年级(上册)第四单元第五节“探索活动:梯形的面积”为例,探索教师应如何践行此模式。
一、数学阅读——认知输入阶段,发现问题
数学阅读是学生进行认知输入的途径[2]。本文的数学阅读是指阅读数学教材中的文字、图画内容,认真观察,捕捉信息,发现问题,输入新知的活动。在“读思达”数学课堂上,教师要依据教学需要,呈现相关的数学“读物”,引导学生阅读。
“探索活动:梯形的面积”这节课的教学重点是使用转化法探索梯形的面积公式。基于此,教师要在课前为学生发放本节课的阅读提纲,助力学生自主阅读。
“探索活动:梯形的面积”阅读提纲
思考问题:可以怎样推导出梯形的面积公式?
阅读任务:请阅读教材内容,勾画关键信息。
阅读观察:在阅读文字信息时,请观察插图,提炼推导梯形面积公式的方法。
阅读思考:在阅读文字和插图的过程中,你有哪些疑问呢?请写下来。
我的问题:
在阅读提纲的指引下,学生自主阅读。尤其,在阅读的过程中,学生做到动脑、动眼,捕捉关键信息,了解推导梯形面积公式的过程和方法,同时发现问题并认真书写记录,做好课堂学习准备工作。
二、数学思考——认知加工阶段,提出、分析问题
(一)提出问题
在前面的认知输入阶段,学生认真阅读,观察并发现了问题。而在认知加工阶段,学生要提出问题。教师是学生提问的引导者。教师要紧抓认知加工阶段,采用适宜的方式提出问题、提出任务等,驱动学生提出问题。
在“探索活动:梯形的面积”这节课上,教师提出任务:“请大家依据‘探索活动:梯形的面积阅读提纲,分享自己发现的问题,并就此说明自己发现的关键信息。”在任务的推动下,学生踊跃表达。有的学生说:“我想知道梯形的面积公式是什么?”其他学生则迁移阅读认知,描述梯形的面积公式。教师趁机引导:“通过阅读教材,大家都了解了梯形的面积公式。看来,我们貌似可以下课了。”此时,大部分学生纷纷表示自己尚有未解决的问题。教师此时应把握时机,鼓励学生提问。在学生提问时,教师在黑板上书写,统计有价值的问题,如“梯形的面积公式为什么要用上底加下底?”“梯形的面积公式是如何推导出来的?”“梯形的面积公式中为什么要‘除以2?”等。在不断提问的过程中,学生的思维愈加活跃,不少学生还由此产生了强烈的探究兴趣。
(二)分析问题
分析问题是学生解决问题的前提。在分析问题时,学生会联想相关内容,并试着提出猜测。在学生提出问题后,教师要给予他们分析问题的机会。
在学生提出系列问题后,教师提出任务:“请大家想一想我们之前学习的平行四边形的面积和三角形的面积内容,归纳推导面积公式的方法,试着分析我们这节课提出的问题,猜想推导梯形面积公式的方法。”在任务的驱动下,学生开放思维,认真想象,在脑海中想象推导平行四边形和三角形面积公式的过程,归纳出方法——将未知面积公式的图形转化为已知面积公式的图形。在归纳方法后,学生自主反思,设想“可以将梯形轉化为哪些已知面积公式的图形”。在设想后,学生继续思考,阅读黑板上的不同问题,认真分析。有的学生说:“可以将两个完全一样的梯形拼成一个平行四边形。这样,梯形的面积就是平行四边形面积的一半,所以梯形的面积要在该平行四边形的面积基础上除以2。”还有的学生提道:“可以将一个梯形切割成一个平行四边形和一个三角形。平行四边形的上底是梯形的上底,平行四边形的下底加三角形的底就是梯形的下底。平行四边形的面积加三角形的面积就是梯形的面积。”在种种猜测下,学生探究欲望高涨,迫切地想要解决问题(可以怎样推导出梯形的面积公式)。同时,在整个问题分析过程中,学生不断想象、反思,灵活地迁移了已有认知,提出猜想,实现了认知加工,无形地锻炼了思维能力。
三、数学表达——认知输出阶段,解决问题
(一)集体交流,解决学习问题
集体交流是学生合作解决问题的方式。集体交流过程包括小组交流、班级交流。在不断交流的过程中,学生会碰撞思维,理清问题解决思路和方法,顺利地解决问题,由此建立良好的数学认知。在“读思达”数学课堂上,教师要在学生分析问题后,组织集体交流活动,使学生合作解决学习问题。
比如,在分析问题的过程中,大部分学生达成共识——要想推导出梯形的面积公式,需要将梯形转化为已知面积公式的平面图形。立足于此,教师鼓励学生与小组成员合作,设想不同的转化方法,并动手操作。在小组合作时,学生纷纷彰显个性化思维,提出不同的看法。面对不同的看法,小组成员进行激烈的交流,得到不同的转化方法。同时,小组成员分工合作,实践不同的转化方法,得出结论。
在既定的小组交流时间结束后,教师组织班级交流活动。在组织活动时,教师鼓励小组毛遂自荐,登台展示本组的交流成果。例如,有小组代表借助电子白板展示了成果。
结合作品,小组代表介绍方法:“我们组使用了拼组法,将两个完全一样的梯形拼成了一个平行四边形。梯形的面积是平行四边形的一半。从图(如图2)中可以看出,平行四边形的底为梯形的上底加下底。平行四边形的高和梯形的高一样。平行四边形的面积是‘(上底+下底)×高。所以,梯形的面积计算方法是‘(上底+下底)×高÷2。”其他小组代表按照如此方式,介绍其他的方法。
经过班级交流,学生了解了“拼组”“割补”法,强化了认知——推导梯形的面积公式,在整个交流过程中,学生积极思维,踊跃表达,锻炼了逻辑思维能力和语言表达能力。
(二)随堂练习,迁移运用
随堂练习是学生解决数学问题的途径。在课堂上,学生体验阅读、思考、表达活动,建构了数学认知。教师要依据学生认知情况,组织随堂练习活动,引导学生迁移运用课堂认知,解决难度不同的问题,借此深化课堂认知,提高问题解决能力。
例如,在学生掌握梯形的面积公式后,教师设计难度不同的随堂练习题。
(1)一张平行四边形白纸底长10 cm,对应高是7 cm。假设将这张平行四边形白纸平均分为两个完全一样的梯形。其中一个梯形的面积是( )cm2。
(2)用两个完全一样的梯形拼出一个平行四边形。所拼出的平行四边形的高是4 cm,底是10 cm。每个梯形的上底与下底之和是( )cm,面积是( )cm2。
(3)一个梯形的面积是78 cm2。如果这个梯形的上底增加3 cm,下底减少3 cm,高不变。那么,这个梯形的面积是( )cm2。
在解决练习题时,学生发散思维,回想课堂学习内容,紧扣梯形的面积公式,分析题目中的已知条件,
把握关键信息,梳理问题解决思路,进而列出算式,细心运算,解决问题。
在学生完成练习题后,教师随机选择代表,鼓励他描述问题解决过程和方法。依据学生的描述情况,教师耐心点拨,助力他们查漏補缺。在体验随堂练习活动的过程中,学生不断思维、表达,锻炼了思维能力、数学运算能力、问题解决能力,同时提高了数学学科核心素养。
(三)布置作业,拓展运用
布置家庭作业的目的之一是使学生拓展思维,灵活运用所学知识。教师要依据学生学习情况,结合数学教学内容,设计开放性的数学作业,驱动学生迁移认知,使用不同的方法解决问题。
例如,在学生学习了梯形的面积公式后,教师紧扣生活背景,设计开放性作业。
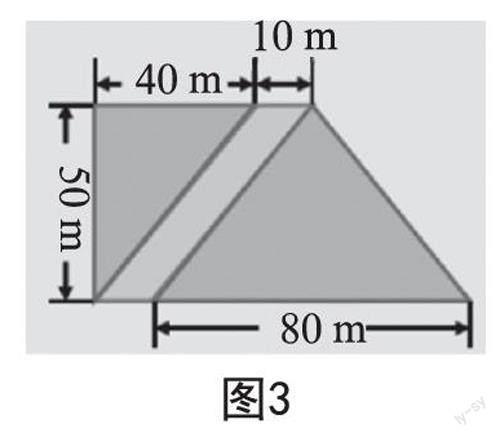
本市准备修建一个综合性公园。公园里有一块梯形草坪,一条景观河穿过这个梯形草坪(如图3所示)。工程队准备为这块草坪铺设草皮。请算出所需要铺设的草皮面积。(至少使用两种方法)
在开放性问题的作用下,学生积极思维,设想不同的思路。
思路一:铺设草坪的面积=左三角形的面积+右三角形的面积。
思路二:去掉景观河,将两个三角形拼凑在一起,得到一个上底为40 m、下底为80 m、高为50 m的梯形。
思路三:用整个梯形草地的面积减去平行四边形(景观河)面积。
在理清思路后,学生有针对性地列出不同的算式,认真运算,得出结果。
在完成作业的过程中,学生始终发挥思维的作用,综合运用数学所学(梯形的面积公式、三角形的面积公式、平行四边形的面积公式),使用不同的方法解决了问题。如此,学生既加深了对所学内容的理解,建构了知识体系,还锻炼了思维能力、数学运算能力、问题解决能力。
四、结束语
总而言之,教师有效实施“读思达”教学,可以使学生经历发现问题、提出问题、分析问题、解决问题这一过程,实现由认知输入到认知加工再到认知输出,由此建构良好的数学认知,发展数学学科核心素养。在小学数学教学中,教师可以将着眼于问题解决的小学数学“读思达”课堂教学模式作为教学“工具”,以阅读、思考、表达过程为切入点,联系数学教学内容,
应用多样的策略,引导学生发现问题、提出问题、分析问题、解决问题,提高学生数学认知水平,发展学生的数学学科核心素养。
参考文献
严慧敏.为“达”而“读” 为“达”而“思”:“读思达”教学法在小学数学解决问题教学中的运用[J].福建教育学院学报,2022,23(2):95-96.
欧健群.读思达教学法在小学数学教学中的应用策略探究[J].考试周刊,2021(96):64-66.
基金项目:本文系2022年度教育部福建师范大学基础教育课程研究中心课题“着眼于问题解决的小学数学‘读思达课堂模式探究”(课题编号:KCA2022245)的研究成果。
作者简介:朱桂云(1975.2-),女,福建邵武人,任教于福建省邵武市水北中心小学,一级教师,本科学历。
