基于“教—学—评”一致性的初中数学概念课教学初探

文/吴 南

初中知识“正方形”为几何概念性知识点，依据笔者以往的教学经验，学生展开此类知识点学习，仍以死记硬背、生搬硬套为主，因此，学生在此知识点的学习过程中，极易出现基本数学概念辨析不清的问题，这就导致在解决问题的过程中思路混乱、概念混淆，甚至解题时无处下手，数学概念课学习效率较低。因此，笔者基于现实需要，一直致力于研究和分析如何有效帮助学生改变这些现状，引导学生跳出机械记忆的桎梏，让学生在自我思考、体会、实践的基础上将抽象概念转变为自我的内在知识，引导学生养成良好的概念学习习惯。因此，在磨课过程中，笔者积极调整思路，总结经验，完善自身对概念教学的理解。

一、教而有基础

教师教学旨在促进学生学习，因此，教师教学设计应以教学课程标准与学生实际学情为基础展开[1]。“正方形”部分知识，作为几何教学的基础图形和重要工具，具有形象直观、知识抽象的特征，因此，《义务教育数学课程标准（2022 年版）》（以下简称《课程标准》）明确指出，要实现对学生逻辑思维能力、几何直观、空间观念等数学思维和核心素养的培养，确保学生学会认识、分析和解决“正方形”相关问题。初中生已经初步具备了几何图形的基础学习能力，有了相对较强的逻辑思维、发散思维、联想、空间想象等能力。此时，学生对类比、归纳、迁移等技巧，也已经有所掌握，所以可以进行难度更大的几何图形概念及性质的学习。在循序渐进的学习之后，学生的概念学习、理解与应用能力必定会有所提升[2]。

二、学而有目标

教师需以《课程标准》与学生实际学情为基础设计教学目标，具体如下。

目标：充分掌握正方形概念、性质及判定；学会用正方形相关知识参与计算；理解正方形与平行四边形、梯形等的关联和区别；基于正方形与平行四边形、梯形等的关联和区别，获得辩证唯物主义教育；逻辑思维能力得以强化。

重点：充分掌握正方形概念、性质及判定，并学会运用相关知识进行解题；正确认识正方形与平行四边形、梯形等的关联和区别。

难点：正确认识正方形与平行四边形、梯形等的关联；学会正方形性质与判定的灵活应用。

三、评而融入教与学

（一）问题驱动学习法

基于问题驱动，从学生较为熟悉的情境或知识出发，引导学生展开“正方形”知识的学习，并让学生通过学与用将问题串联起来，每组问题对应不同的教学目标，既实现了教学目标，也完成了对教学目标是否实现的评价。

问题1：分析下列图形（如图1），简要说明图形的名称、作用，并思考除了矩形与菱形外，生活中还有哪些常见的特殊四边形？这些特殊四边形有什么特点？

图1 看图思考

问题2：下列说法中正确的是（ ）

A.相等角必定为对顶角

B.四角均相等的四边形一定为正方形

C.平行四边形对角线互相平分

D.矩形对角线一定垂直

问题3：已知四边形BCDF为平行四边形，现有以下①BC=CD，②∠BCD为90°，③BD=CF，④BD⊥CF作为补充条件，试选其二，让平行四边形BCDF为正方形，则下列选项中错误的是（ ）

A.选①② B.选②③ C.选①③ D.选②④

问题4：如图2 所示，正方形ABCD中，E、F分别为过AB、BC的点，若存在AE+CF=EF，试求出∠EDF。

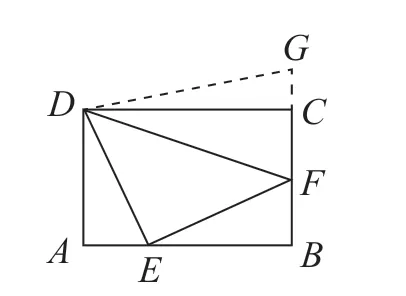
图2

问题5：如图3，在△ABC中，AB=AC，点D是边BC的中点，过点A、D分别作BC与AB的平行线，并交于点E，连接EC、AD。求证：四边形ADCE是矩形。

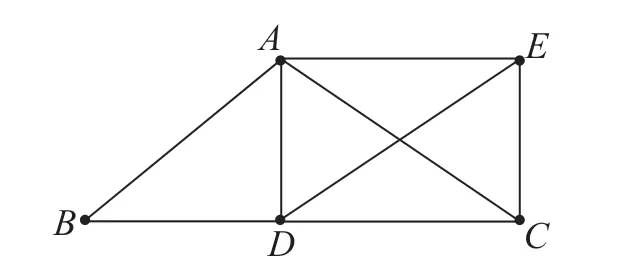
图3

思考：（1）生活中经常会见到哪些图形？哪些更特殊？（2）正方形的特征是哪些？如何判定？（3）是否掌握了正方形的概念、判定及与菱形等的联系区别？

在此环节中，学生可以通过小组讨论的形式，对正方形的相关概念展开学习。教师还可以鼓励学生针对同一个例题进行创新，让学生发现数学学习的趣味性。另外，教师还应该进行适度拓展，将与现实生活相关的数学题目引入课堂教学，丰富学生学习领域和方法，引导学生学以致用。

设计说明：在教学中，教师需尽量避免强迫学生学习，应该采用灵活、有针对性的办法来激发学生的学习兴趣，让学生学会主动学习。如此，学生的内生学习动力才能充足，学习效率才会有所提升。当然，数学教学亦不可单纯强调对学生的学习兴趣培养，而是应该将兴趣培养与学习内容、学习方法、学习结果等融于一体，这样才能够基于学生被激发的学习兴趣，而将知识引入其他教学活动中，让学生将知识与生活连接起来，进而达到学以致用的目的。

（二）动手实践学习法

教育心理学研究表明，学生在处于丰富探究活动中时，才能更好地学习空间概念和几何图形等[3]。因此，教师还应该重视组织学生参与动手实践，让学生在这一过程中尝试、想象、推理、验证、思考、抽象，掌握概念的实质。

问题6：如图4 所示，将正方形ABCD四边的中点顺次连接，得到四边形EFGH，试求证EFGH四边形为正方形。

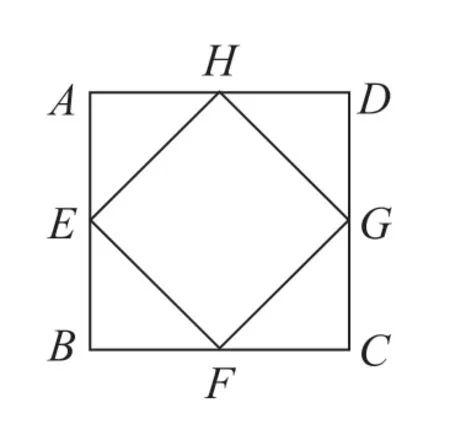
图4

问题7：如图5 所示，将正方形ABCD四边的四个点E、F、G、H顺次连接起来，且AE=BF=CG=DH，此时得一四边形EFGH，试求证此四边形EFGH为正方形。

思考：（1）动手将抽象问题通过裁剪具象化；（2）两个四边形各自有何特点？是否均为正方形？该如何证明？

在此环节中，学生需要将动手与观察、思考、推理证明等学习行为结合起来，这对于引导学生通过数学符号进行严谨的逻辑推理有积极价值。

设计说明：让学生在初中数学学习中动手操作，既可以启迪学生思维，让学生思维充分为操作服务，也能够引导学生手眼、手脑、眼脑并用，让学生实现知识掌握感性到理性的认知升华，推动学生反复思考、论证数学概念和知识，提升学生的数学学科核心素养。

（三）评价承前启后法

教师评价任务的实施，应强调承前启后，为学生后续学习奠定基础。

后来她读书，进城，毕业，工作，再后来她遇见秦川。一颗英俊的脑袋从出租车里探出来，对她说，顺路。她立即汗透全身，心中酥痒。她知道她爱上了他。

问题8：如图6 所示，边长为2 的5 个正方形如下摆放，其中A、B、C、D均为正方形对角线交点，求图中阴影部分面积大小。

图6

问题9：如图7 所示，正方形ABCD对角线AC、BD均交于点O，两点E、F分别在边线AB、BC上，∠EOF=90°。

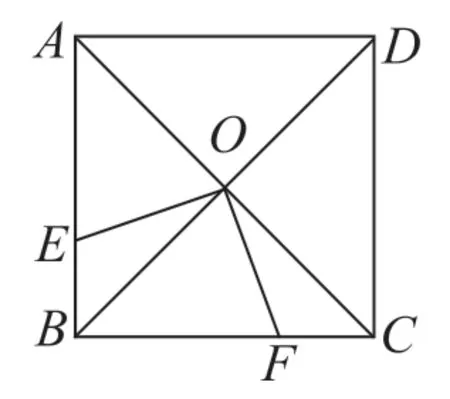
图7

（1）试证明OB=OF；

（2）AE=BF是否成立，如成立请证明；

（3）BE=BF是否成立，如成立请证明；

（4）AE2+CF2=OE2是否成立，如成立请证明。

学生仍以小组讨论研究的形式完成此部分练习内容，在此过程中，教师及时进行巡视，解答学生发现的问题。

设计说明：问题8 与问题9 除了涉及正方形的概念、判定等内容外，还涉及“证明相关线段长度的等量关系”等知识，这样的问题设计及解决，既达到了对学生课堂已学知识的检测和巩固，也在一定程度上增加了试题难度，考虑到了对不同层次学生的问题解决能力和学习现实需要的考查，对于提升教师教学质量有积极价值。

四、课后启示与反思

第一，知识学习以概念为伊始，知识获得则需要学生进行感知、观察、实践、体会与总结。在新课设计中，教师使学生深刻认知到知识形成的过程是自然的、循序渐进的、水到渠成的。因此，教师的教学设计至关重要。教师务必以《课程标准》为基础和依据，充分结合学生的实际学情，细致深入地分析教材，为“教好”奠定基础。

第二，教师是教学引导者，学生是学习主体，合理的教学设计极有必要。在教学设计中，教师应关注具体的设计是否达到了促进学生学习的目的。此外，教师还应积极鼓励学生自主探索，凸出学生的学习主体地位，积极动员学生主动参与，认真讨论问题，提出疑问，有效解决问题，促成学生合作学习，让学生在多元化的学习方式中感受数学学习的乐趣。

第三，在教学过程中，教师还应该学会充分利用“旧知识”与“旧知识的形成过程”，在引导学生及时复习已学知识的同时，充分利用“旧知识”，探索出全新的待学知识，在此过程中引导学生获得新知识，体会“新旧”知识间的关联性和变化性，在无形中达到学生数学学科思维方式锻炼和培养的目的，提升学生的思维能力。

五、结束语

要实现“教—学—评”一致性，教师一方面应做好自身教育实践工作，弱化自身的教育主导地位，体现自身的教学引导作用，做好对学生的学习引导，让学生在自主学习提升过程中，及时纠错和优化；另一方面，应凸显学生的学习主体地位，尽可能鼓励学生自主学习、自主探究、自主解决问题，以学生对知识的渴求为内生动力，让学生获得良好的学习能力，而不再是跟着教师步伐进行学习。另外，在教学中，教师还应高度落实教学评价，采用课堂评、课后评、作业评、表现评、参与评等多元化的评价形式来构建全面的、完整的数学概念学习评价体系，及时验证教学模式的可行性，为教学实践的优化完善提供思路，推动教育改革发展。