分类讨论法在初中数学二次函数教学中的运用

2023-08-23黄建武

名师在线 2023年21期

文/黄建武

分类讨论法作为初中阶段应用较多的教学方法，是数学思想的具体体现，也是数学课堂的教学重点[1]。帮助学生在分类讨论教学活动中学习教学知识，是教师可以采取的一种教学方法，也是教师在教学中的创新。二次函数是函数知识学习的基础。笔者结合自身教学实践经验，对分类讨论法在初中数学二次函数教学中的应用展开探讨，并结合实际教学案例加以分析，以供各位读者阅读参考。

一、分类讨论思想在正向型函数教学中的应用

正向型函数是指已知二次函数的定义域及区间，求取二次函数的最值。为高效完成这一问题的讲解，教师可以根据题目中函数对称轴与定义域区间之间的位置关系组织学生展开分类讨论活动。正向型函数教学的讨论过程可以分为三个项目，即轴定区间定、轴定区间动和轴动区间定。

（一）轴定区间定

“轴定区间定”这一情况是指，在已知二次函数的情况下，根据所给出的固定定义域区间，计算二次函数在定区间上的最值。

例1：函数y=-x2+4x-2 在区间[0，3]上的最大值和最小值分别是多少？

首先，教师可引导学生根据所给出的函数进行简化，要求学生将题目中的函数转化为另一种常见形式。在学生将函数转化为y=-x2+4x-2=-（x-2）2+2 后，教师便可以进一步要求学生根据函数方程式的特征，对函数的图像进行简单的分析。学生在教师的提醒下可以得到相应的信息，如函数对称轴方程式为x=2，顶点坐标为（2，2），且函数图像开口向下。之后，教师便可以引导学生将基本信息与题目要求相结合。学生根据题目所给出的区间判断顶点横坐标与区间之间的位置，并得到题目中函数的顶点横坐标位于给定的区间范围之内。当明确顶点横坐标与给定区间范围之间的位置关系之后，教师便可以进一步引导学生根据之前所获得的函数图像信息，绘制出简单的函数图像，并结合题目要求得到题目答案。学生作图如下：

如图1 所示，函数的最大值为f（2）=2，最小值为f（0）=-2。

在讲解完例题之后，教师便可延伸题目，应用分类讨论思想，帮助学生学习更多不同题目的解题方法。仍以这道题为例，教师可以更换题目中的区间范围，并延伸出顶点横坐标不位于区间范围之内的另一种情况。结合以上解题过程以及解题过程中所绘出的图像，学生能够在较快时间内掌握相应的解题方法，并得到答案。

（二）轴定区间动

“轴定区间动”是指在已知二次函数的情况下，根据所给出的定义域区间，计算二次函数在区间上的最值，题目中所给出的定义域区间随参数变化。

例2：求函数f（x）=x2-2x+3 在x∈[a，a+2]上的最大值和最小值。

与“轴定区间定”问题的解题思路相同，首先教师可引导学生将函数方程式进行格式上的转化，并根据所转化出的方程得到函数图像的基本信息。学生在完成函数方程式的转化之后，可知这一函数图像开口向上，其对称轴为x=1。之后教师便可引导学生根据所给区间进行分类分析。教师可引导学生将定区间中的a值与对称轴x=1 联系，并延伸出不同的分类讨论内容。

首先，学生分析当x=a时，a距离对称轴x=1 最近，a+2 距离对称轴x=1 最远。因此，当x=a时，ymin=-a2+3，ymax=a2+2a+3。

其次，学生便可进行分类分析：①当0＜a≤1 时，1距对称轴x=1 最近，a+2 距离x=1 最远。因此，当x=1时，ymin=2，x=a+2 时，ymax=a2+2a+3。②当-1＜a≤0时，1 距对称轴x=1 最近，a距x=1 最远。因此，当x=1 时，ymin=2，ymax=a2-2a+3。 ③当a≤-1 时，a+2距对称轴x=1 最近，a距x=1 最远。因此，当x=a+2时，ymin=a2+2a+3，x=a时，ymax=a2-2a+3。

最后，教师可以组织学生根据二次函数区间图像进行总结：

当a＞0 时，

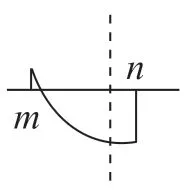
图2

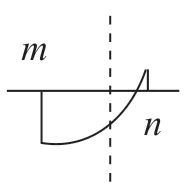
图3

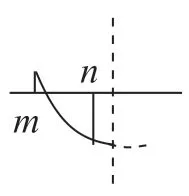
图4

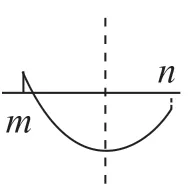
图5

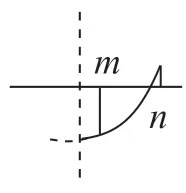
图6

当a＜0 时，

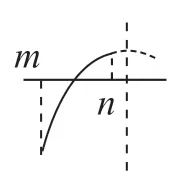
图7

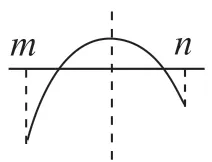
图8

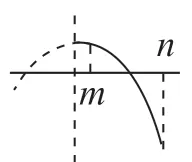
图9

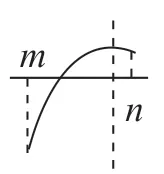
图10

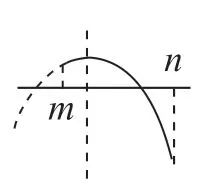
图11

（三）轴动区间定

“轴动区间定”这一情况是指，在已知二次函数的情况下，根据所给出的定义域区间，计算二次函数在区间上的最值。定义域区间为题目给定区间不变，但二次函数图像随参数变化而变化。

例3：求函数f（x）=x2-2ax+3 在x∈[0，4]上的最值。

首先，教师可引导学生将函数方程式进行格式上的转化，并根据所转化出的方程得到函数图像的基本信息。其次，学生在完成函数方程式的转化后，可知这一函数的图像开口向上，其对称轴为x=a。最后教师便可依据分类讨论流程，组织学生根据题目要求和所给信息进行分类讨论：①当a＜0 时，0 距对称轴x=a最近，4 距对称轴x=a最远。因此，x=0 时，ymin=3，x=4时，ymax=19-8a。②当0 ≤a＜2 时，a距对称轴x=a最近，4 距对称轴x=a最远。因此，x=a时，ymin=3-a2，x=4时，ymax=19-8a。③当2 ≤a＜4 时，a距对称轴x=a最近，0 距对称轴x=a最远。因此，x=a时，ymin=3-a2，x=0时，ymax=3。④当4 ≤a 时，4 距对称轴x=a最近，0距对称轴x=a最远。因此，x=4 时，ymin=19-8a，x=0时，ymax=3。

通过讲解这三种正向型函数的题目，学生能够简单了解分类讨论思想在数学解题过程中的应用，有意识地将分类讨论的方法应用于自己的实际解题过程中。

二、“二次函数y=ax2（a ≠0）的图像与性质”案例研究

（一）课程分析

1.教学内容分析

本课内容要求学生能够应用描点法画出二次函数y=ax2（a≠0）的图像，并能够根据图像认识和理解二次函数的相关特征。在课堂教学过程之中，教师应培养学生的探究能力，引导学生探索二次函数y=ax2的图像和图像特征，并引导学生体会分类讨论的思想和方法。

2.学生需求分析

学生通过学习本课内容能够掌握二次函数y=ax2基本的图像与性质。除此之外，通过课堂学习过程中体会分类讨论思想，学生能够在数学学习方面获得更加多样的学习方法，同时也能够在合作和分工的过程中体会到合作的重要性，综合发展自身的素质和能力。

3.教学工具需求分析

在教学过程中，教师需要借助多媒体向学生展示二次函数y=ax2（a≠0）的图像，同时也需要在黑板或多媒体显示屏上向学生示范二次函数y=ax2图像的绘画过程，并借助图像对二次函数的性质展开讲解。

（二）实际教学流程

1.环节一：描点绘图

首先，教师可通过提问的方式，引导学生复习之前的内容，并引入本堂课教学知识：“我们在之前学习了二次函数这一概念，那么二次函数的定义是什么呢？今天的学习内容是二次函数的图像，我们在之前学习过一次函数的图像，那么一次函数的图像是什么形状呢？我们又是怎样绘制出一次函数的图像呢？教师”通过这样的复习提问引入，能够使学生在课堂上提出描点绘图。

（1）列表：设定x取值并计算y值，列出函数的对应值表（见表1）。

表1

（2）描点：根据所列出的函数取值与对应值，在平面直角坐标系中画出点的位置。（点位如图12 所示）

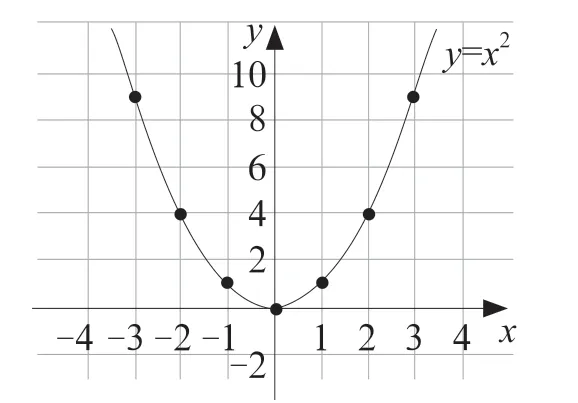
图12

（3）连线：连接各点，并保证曲线光滑，得到函数y=x2的图像。

在班级内所有学生完成二次函数y=x2的图像之后，教师便可以将学生分为若干个小组，并要求学生依据相同的方法绘制y=2x2、y=-2x2与y=-x2的函数图像。

2.环节二：归纳共性

教师可提问学生：“刚刚大家依照描点绘图的方法绘制出了二次函数的图像，请大家以小组为单位，将这4 个函数图像汇总在一起并讨论归纳这些函数图像的共性。”学生在讨论过程中加以总结归纳：“这4 个函数图像的对称轴都是y轴，函数顶点位于原点，函数图像的开口方向与x前的数字正负值有关。”

3.环节三：探究本质

教师可以将这四个函数图像展示在黑板或多媒体显示设备上，并引导学生共同归纳y=ax2的图像与性质。

4.环节四：例题解析

（1）写一个顶点在原点，开口向上的二次函数关系式。（2）画出图像并回答问题：抛物线y=2x2顶点坐标是什么？对称轴是什么？当x=？时，函数值最小，函数最小值是多少？抛物线y=2x2（顶点除外）在x轴的上方还是下方？（3）请你在不画出图像的前提下写出y=-3x2和y=3x2的顶点坐标、对称轴以及函数图像的开口方向。

5.环节五：课堂总结

教师：“这堂课上，我们对二次函数y=ax2（a≠0）中的a的值进行分类，并展开了关于对应图像的讨论。通过这一分类讨论过程，我们总结出y=ax2的顶点是原点，坐标轴是y轴，开口方向与a的值之间的关系。”