变中抓不变——较复杂的分数应用题教学策略

江苏江阴市晨光实验小学（214433） 陈 英

较复杂的分数应用题中往往有很多变化的量，教师可以变问题、变条件、变内容，通过举一反三，引导学生主动联结知识间的联系，深入分析问题，在比较辨析中真正领悟“变中抓不变”的数学思想方法，切实提高学生分析问题、解决问题能力。

一、问题凝视

教材在六年级分数单元编排了思考题：学校田径队女生人数原来占田径队总人数的后来有6名女生加入，这样女生人数就占田径队总人数的现在田径队有女生多少人？

初读题目，学生以为很简单，误认为单位“1”总人数没有发生变化，6 人对应的分率是导致错误。事实上，“又来了6 名女生”使得数量关系发生了变化和两个分率对应单位“1”的实际数量也就不同。

二、成因透视

1.题目数量关系复杂

上题以思考题的形式出现，就说明它具有一定的综合性，体现在“又有6 名女生加入”这个动态变化的量，一下子提高了题目的难度系数。学生理不清数量关系，自然找不到正确的解题方法。此题从字面上看只描述了女生人数和总人数，其实还隐藏着男生人数这个量。由于有6 名女生加入，引起女生人数发生了变化，总人数也随之发生了变化。如果还是从总人数这个变量入手，会给解题带来很大的困难。若仔细分析题中的条件，就会发现男生人数不变这个条件，也就是男生人数前后都没有发生变化。因此，解题关键是紧抓男生人数这个不变量，巧妙计算现在女生人数。

2.学生思维水平不足

小学生的思维正处于直观形象思维向抽象逻辑思维的过渡阶段。教材中只编排的单位“1”已知的两步计算的分数应用题教学，而省略了单位“1”未知的两步计算的分数应用题教学。学生对需要两步计算的分数除法问题还处在通过画线段图来理解单位“1”的阶段，而一下子跃到动态变化的量——单位“1”发生改变，需要跳跃性的思维，但大部分学生的思维还没达到这水平。

三、出路审视

1.找准知识衔接点

学生觉得分数应用题很难，这很正常，因为学生在生活中很少遇到关于分数的问题。对此，教师不妨换个角度，从学生实际的认知水平入手，把分数知识转化成学生擅长的整数知识。比如，利用分数和比的联系将“学校田径队女生人数原来占田径队总人数的的“转化成1∶3，也就是把学校田径队女生看作1份，总数看作3份；当然还能把男生看作2份，所以女生人数是男生人数的同理，当女生人数发生变化，占田径队总人数的时，把学校田径队现在女生人数看作4份，总数看作9份，男生人数就可以看作5 份，所以女生人数是男生人数的

2.紧扣知识关键点

对较复杂的分数应用题，用常规的分析思路解题往往比较困难，教师可引导学生在变化中抓不变，让不变量化隐为显。女生人数和总人数是思考题中动态变化的量，但变化中隐含着某个不变量，就是男生人数始终不变。找准男生这个不变量是解题的关键点，求出男生人数后，女生人数也就顺利得到解决。

3.挖掘知识发散点

数学教学，不仅仅是让学生学会解答某一个思考题，更要让学生掌握解决这类问题的数学思想方法和举一反三的能力。可把题目变“三变”，引申出题组练习，让学生在变化中真正理解“变中抓不变”的数学思想方法。一变，变问题。把问题变成“原来田径队有女生多少人？”“现在田径队一共多少人？”；二变，变条件。本题是男生人数不变，也就是其中一个量是不变量，改变条件后，呈现另外两种类型：和是不变量，差是不变量。三变，变内容。把问题拓展到浓度问题、百分率问题等，这些问题虽然情境不同，但本质相同，都是需要抓住不变量来解题。通过这些“变”，就能切实提高学生解决实际问题的能力。

四、教学重构

1.深入浅出，理解本质

（1）旧分率转化成份数

师：根据分数和比的联系，看到这句话“学校田径队女生人数原来占，你能想到什么？

生2：除了女生人数和总数，还能想到男生人数占了2份。师：看到“女生人数就占田径队总人数的这句话呢？

生3：可以把学校田径队女生人数看作4份，男生人数看作5份，总数看作9份。

师：根据分数和比之间的关系，可以把分数应用题转化成整数应用题来解答。女生人数前后发生变化，总人数也随之发生变化，什么没变？

生4：男生人数没变。

生5：虽然把原来的男生人数看作2份，把后来的男生人数看作5 份，但是男生人数不变，为方便计算，把男生人数统一成10份。

师：把男生人数前后统一成10 份，根据比的基本性质，女生人数前后的份数发生什么变化？

生6：原来的女生人数调整为5份，现在的女生人数调整为8份。

师：正因为有6 名女生加入，所以女生人数由原来的5份增加到8份，你想到了什么？

生7：3 份女生人数是6 人，所以一份女生人数是2人。

生8：现在田径队女生人数占8 份，一份2 人，所以现在女生有16人。

师：我们可以把解题思路整理成表格。（见表1）

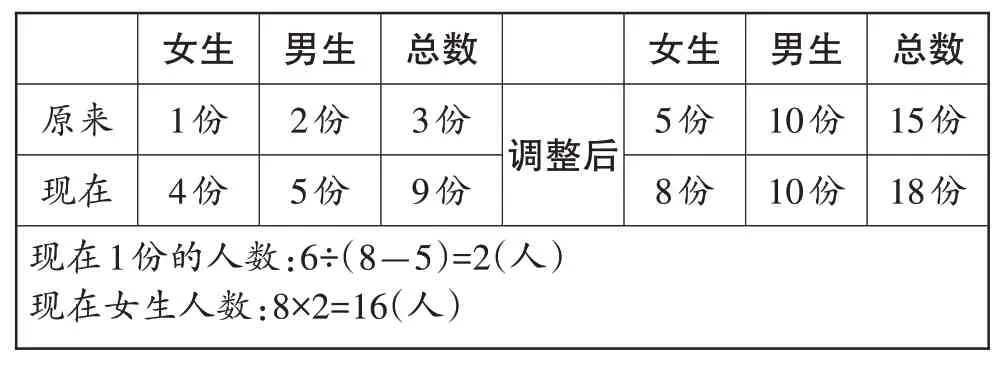
表1 解题思路分析表

（2）旧分率转化成新分率

师：刚才我们紧扣不变量，把旧分率转化成份数来解决问题。其实也可以把旧分率转化成新分率来解决问题。大家都试一试。

生9：男生人数是不变量，把男生人数看作单位“1”。

2.变式练习，举一反三

（1）变问题

师：如果把问题改成现在田径队一共有多少人？你会解答吗？

生1：解题思路不变。现在田径队人数一共有18份，所以总人数为2×18=36（人）。

师：你还能提什么问题？如何解答你提出的问题？

生2：原来田径队一共有多少人？原来田径队一共占15份，所以田径队一共有2×15=30（人）。

生3：原来田径队女生有多少人？原来田径队女生占5份，所以原来田径队女生有2×5=10（人）。

生4：田径队男生多少人？田径队男生占10份，所以田径队男生有2×10=20（人）。

师：大家真了不起，提出了这么多问题。这些问题有什么共同点？

生5：问题虽然有变化，但解题思路相同，都是先找准男生人数这个不变量，再求出一份有几人，最后看有这样的几份。

（2）变条件

师：如果把条件改一改，你还能看出谁是不变量吗？

生6：因为训练人员发生了变化，休息人员也跟着变化，而田径队总人数没有发生变化，也就是本题的不变量是总数。

师：把条件再改一下，看看不变量是什么？学校田径队女生人数是男生的，各离队6人，这时女生人数是男生的田径队原有男、女生各多少人？

生7：因为各离队6 人，男生人数发生了变化，女生人数也发生了变化，总人数也随之变化，但男女人数的差没有发生变化，也就是本题的不变量是男生和女生人数的相差数。

题目千变万化，会做一道题，并不代表掌握了。通过“三变”条件，让学生真正领悟“变中抓不变”思想：求变是为了更好地建构，在变化中迅速捕捉不变量，不变量可以是“和不变”“差不变”“部分量不变”等。

（3）变内容

出示题目：有一杯200 克的盐水，盐的质量占盐水的20%，加了一些水后，盐的质量占盐水的12.5%，求加了多少克的水。

生8：加了一些水后，水的质量变化了，随之盐水的质量也变化了，但盐的质量是不变的。

师：刚才是加水使浓度降低，如果是通过蒸发使水减少呢？

出示题目：宾宾在科学课上配制了含盐16%的盐水200 克。结果发现盐水的浓度低了，需要用酒精加热，使水蒸发。如果要使盐水的含盐率提高到20%，需要蒸发掉多少克水？

生9：蒸发了一些水后，水的质量变化了，随之盐水的质量也变化了，但盐的质量是不变的。

生10：在盐不变的情况下，不管是添加水还是蒸发水，都会引起浓度变化，要解决问题，还要在变化中紧扣不变量，抓不变量是解题关键。

师：同一种零件，张师傅做了20 个，经检验，合格率为80%。为使合格率提高到95%，张师傅应连续生产多少个合格产品？这题的变量和不变量又是什么呢？

生11：合格率由80%提高至95%，合格的产品数量发生变化，零件总数也发生变化，但不合格的产品数量不变。抓住不合格产品数量是解题关键。

通过变问题、变条件、变内容，让学生深入分析问题实质，精准把握解题关键。学生通过举一反三，感悟更加深刻，解题思路更加清晰，认知结构也更加完善，在变化中抓不变量这一数学思想方法已在心中生根。

综上所述，解决较复杂的分数应用题时，要让学生根据题中的已知条件分析数量关系，以不变量作为突破口，以达到事半功倍的效果。“变中抓不变”的数学思想方法不仅可以拓宽学生的解题思路，还可以在解题过程中加深学生对基础知识的理解、建立知识之间的联系、提高解决实际问题的能力。