依托几何直观 助力数学理解——一道题引发的思考

江苏无锡市锡山实验小学（214104） 安 蕾

在一次毕业考试中有这样一道题：

小明学习了乘法分配律之后，这样来计算“25.2×4.5”：

25.2×4.5

=2.5×4+0.2×0.5

=100+0.1

=100.1

后来他用竖式验算，发现这样计算的结果是错的。你能结合下图（如图1）来说明为什么这样计算“25.2×4.5”是错的吗？

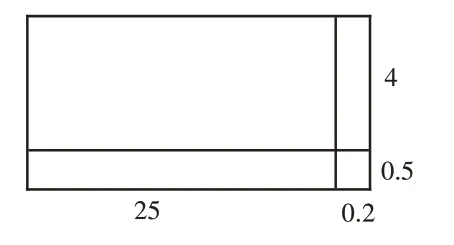
图1

笔者抽取了本校参加毕业考试的学号末位是3 和5 的学生的答题情况，发现得分率是57.6%，学生的错误主要有三种情况：（1）完全不懂如何结合图形来解释，也不知道错在哪里；（2）会用乘法分配律解答，但不懂如何用图形来解释；（3）能结合图形来解释长方形的面积，但是不能用数形结合的方式解读算理和算法。

心理学研究表明，小学生以直观形象思维为主，面对抽象的数学知识，需要借助直观的感性材料，让数学问题由抽象转化为形象，让数学道理从感性走向理性。结合教学实践，笔者从以下三个方面来谈谈自己的所思与所得。

一、依托几何直观，理解算理分析

数学算式是数学问题的高度概括，是抽象化、符号化的语言，而算理指的是计算过程中的道理。简而言之，就是让学生明白“为什么这样算，运算的意义和逻辑是什么”。几何直观是利用图形描述和分析数学问题，让学生在直观图形的基础上理解运算的可行性和逻辑性。教学过程中，教师可引导学生依托直观的“图”去思考抽象的“理”，通过自主探索、发现和再创造，经历体验和感受数学发现的过程，使学生最终实现对算理的深层建构。

【案例】苏教版教材三年级上册“两、三位数除以一位数”的例题1 是首位能整除的两、三位数除以一位数，学生解题时往往不明白建构“两层楼”的必要性，只是按照教师的要求依葫芦画瓢。笔者在教学时将教材中的例2 前置，带领学生经历“16 除以2”“46 除以2”“56 除以2”三个阶段，引导学生细细品味三个“除以2”的不同，从而明白“计算过程需要分两步，竖式计算分两层更加清晰”。

出示题目（如图2）：将16 个羽毛球平均分给两个班，每班分得多少个？

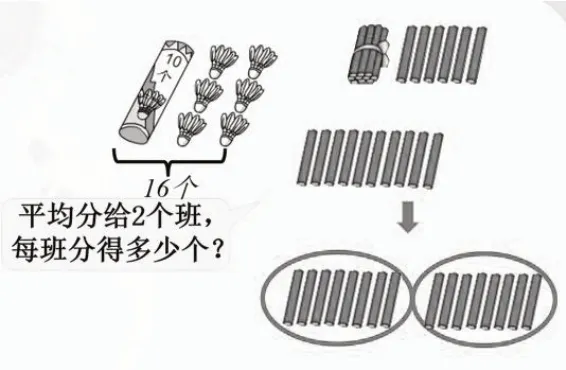
图2

师：为什么要将一捆拆开？

师：16÷2 竖式怎么写？（出示图3）商“8”表示什么？二八十六，一共分掉了几个？

图3

师：一般先想想商几，再乘一乘，看看分掉了多少，最后减一减，看看有没有分完。

出示题目：将46 个羽毛球平均分给两个班，每班分得多少个？

师：46÷2 等于多少？同桌合作，用小棒摆一摆，说一说是怎么算的。

师：有位同学写的是“40÷2=20，6÷2=3，20+3=23”。从算式中可以看出他分了几次？

师：不管是用小棒分，还是用算式算，我们都是先分4 个十，再分6 个一。像这样分的过程可以用竖式来表示，46÷2先算十位，4÷2=2，2写在十位上；再算个位6÷2=3，3写在个位上，等于23。

出示题目：将56 个羽毛球平均分给两个班，每班分得多少个？

师：尝试用竖式计算，有困难的同学可以借助分一分小棒理解。

师（出示图4）：理一理分的过程和每一步的含义。

图4

师：不知不觉间，我们像造楼房一样，把竖式写成了2 层。为什么要创造2 层的竖式呢？显然，第一层解决分十位的5 个十时，还剩1 个十；第二层，把十位余下的1 个十和6 个一合起来再分，很清楚地表示分了两次。

师：现在回过来想想，46 除以2，平均分了两次，用“一层楼”很快就算出了答案。那么，怎样能一眼看出分了两次呢？

……

通过几何直观引导学生以图解数、以图思数，把算式变成图形，用图形来解释算理，化抽象为形象。对于“笔算两三位数除以一位数竖式为什么这样写？”，学生在由数到图，又由图回到数的过程中找到了答案。这样的表征使学生对竖式的每一步算理都了然于心，对竖式的每一步算法都明明白白。

二、依托几何直观，理解问题表征

从数学知识的角度来看，几何直观是借助直观的图形将已知信息进行分析，并且找到数学要素之间的关联性，深化对数学问题的理解，把复杂的数学问题变得简明、形象，真正把握问题的实质。

【案例】苏教版教材五年级下册“解决问题的策略（转化）”

师：比一比，看谁算得又对又简单。能不能用转化成图形的方法说明道理？（学生给出了画圆形图、线段图、正方形图等方法）

师：还记得我们学习分数和小数时，借助哪个图形最能化繁为简，润数于形？（学生纷纷想到了正方形）

图5

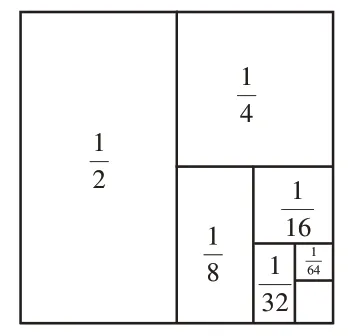
图6

师：192+96+48+24+12，你会算吗？请画图说明。

学生作品（如图7-1、7-2、7-3）：

图7-1

图7-2

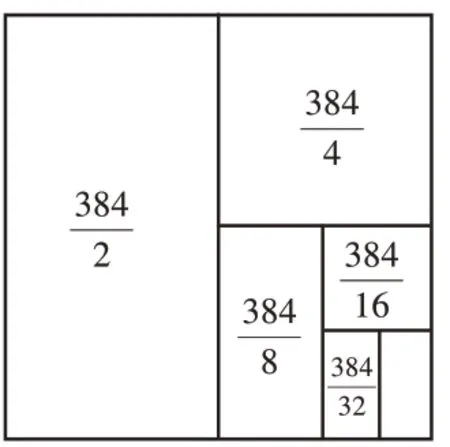
图7-3

师：结合例题，想想我们画的这些图，你有什么想说的？

……

借助几何直观将数学问题形象化，将数和形巧妙结合起来，化隐为显，使学生亲历转化的过程，在对图形理解中完成自我知识框架的重建。看似与图形没有任何关系的数学问题，转化成图形后不仅避开了复杂的运算，还提升了学生思维的深度。有了这样的体验，学生再遇到类似的题目，就能通过图形理解计算原理。

三、依托几何直观，理解概念本质

概念教学是数学教学的难点，因为小学生以形象思维为主，所以理解抽象的概念有很大的难度。借助直观图形能把抽象的概念形象化，帮助学生在直观中理解抽象的数学知识。

【案例】苏教版教材六年级下册“认识正比例”在例题中呈现的是静态的关于时间和路程的表格（如图8）：

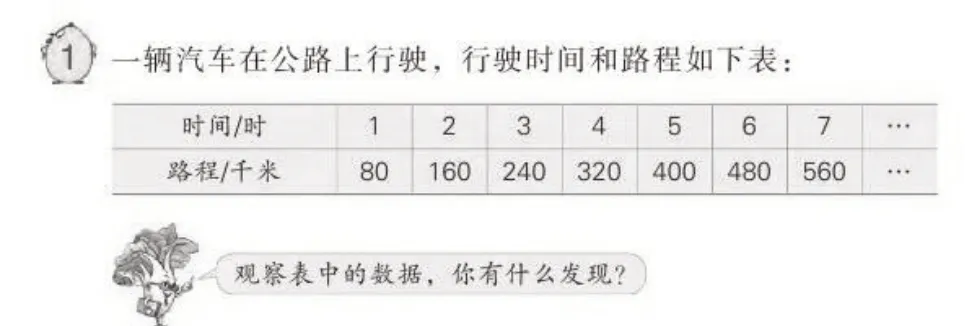
图8

这是以静态的表格方式，从数据分析的角度来揭示正比的概念。然而，任何概念的获得都需要经历充分的感知过程，感知越充分，概念的本质越清晰，理解越深刻。

师（出示直观的注水动态情境，如图9 所示）：你看到了哪些量？什么变了？什么没变？

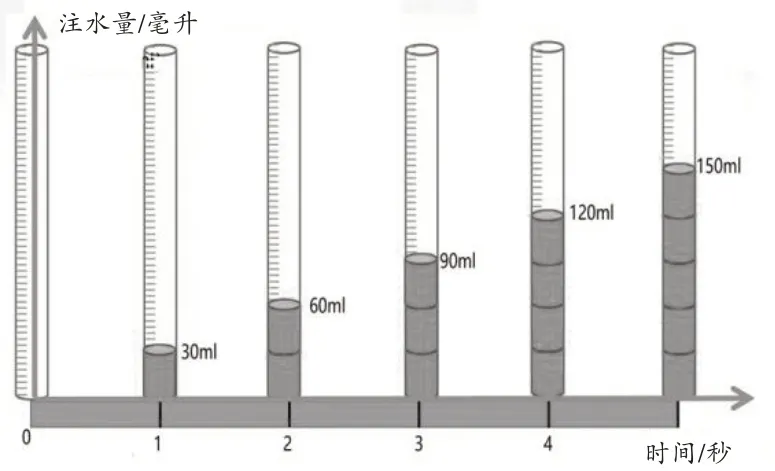
图9

师：时间在变，注水量也在变，但是注水速度不变，都是每秒30 毫升。照这样计算，6 秒呢？7 秒呢？……100 秒呢？（利用图形表征变量，展现两个量之间的相互依存关系，正比例的意义不再局限于“数”式的计算，更从“形”意上得到了诠释）

师（出示图10）：总价和数量是两种相关联的量，随着数量的增长（减少），总价也在增长（减少），即它们是同增同减的。

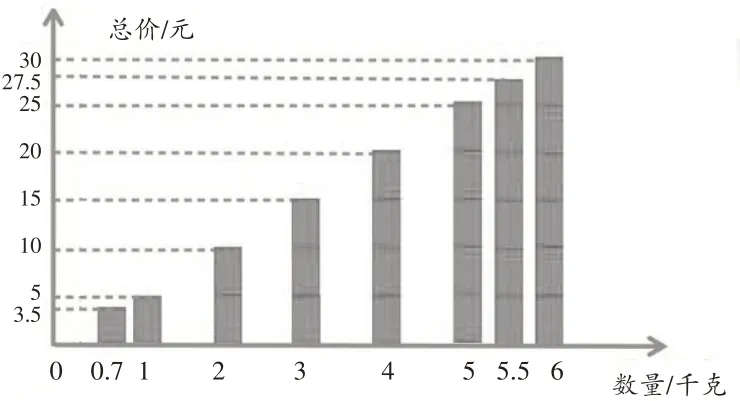
图10

师：照这样计算，如果购买的是0.7 千克，对应的总价是多少？购买5.5千克，对应的总价是多少？……

（当图10 中的数量取值越变越多，总价所对应的柱形像小树林一样有序生长，越来越密集，学生从直观图中感悟到“正比例的特征除了对应性还存在连续性”）

师（出示图11）：随着时间、路程对应的变化，表示速度的点（条状的上端点）越来越密集，直到最后变成一条直线……

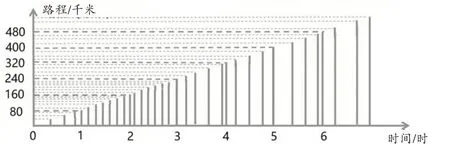
图11

在图形展示的环节中，通过形象的“图说”到抽象的正比例概念的深度表征，几何直观让无形的概念本质显形，既加深了学生对正比例概念的理解，又回归到知识发生的源头，沟通了知识元素之间的联系。

曹培英在《跨越断层走出误区——“数学课程标准”核心词的解读与实践研究》一书中提到：“一方面，直观是数学抽象的基础与数学认知的有力支撑；另一方面，直观又是数学理解，乃至数学抽象的重要内涵与数学本质认识的深化。”在教学中，教师要善于结合教材资源，基于学生的认知水平，帮助学生自觉运用几何直观探究数学问题，将抽象的数学知识转化为图形、符号，化抽象为具象，从无形到有形，提高学生对数学知识、逻辑的理解能力，提升学生的数学素养。