电弧增材制造封闭路径控制策略研究

卢楚文，牛犇，王凯，曹运成，易江龙

1.佛山科学技术学院 广东佛山 528225

2.广东省科学院中乌焊接研究所，广东省现代焊接技术重点实验室 广东广州 510650

1 序言

电弧增材制造技术是以焊接电弧为热源，按规划好的运行轨迹在运动执行结构的带动下逐层堆积，直到获得符合要求的成形件，是一种从无到有的逐层累积叠加制造技术[1-3]。合理的路径规划是保证电弧增材制造中金属件成形的重要环节，也可以减少或消除成形过程产生的内应力。目前，电弧增材制造环节中存在封闭路径闭合处搭接不平、非封闭路径熄弧端塌陷、单道多层成形件两端塌陷，以及中间凸起等成形问题。

为解决电弧增材制造环节的成形问题，国内外学者都进行了相应的研究，美国肯塔基大学ZHANG等[4]对堆焊工艺研究后，提出了自适应切片方法，自动分析模型结构的特点，进而确定切片的厚度，最终制造出的实体零件和零件三维模型的尺寸差异较小。哈尔滨工业大学熊俊[5]采用GAM增材制造技术研究了工艺参数对单道多层成形形貌的影响，针对起弧端和熄弧端高度差距大的问题，提出封闭路径采用搭接长度过度补偿的熔敷方式，并给出了搭接长度的具体数值；非封闭路径采用平行往复的熔敷方式。南京理工大学尹凡[6]在对多层堆敷成形工艺及尺寸控制研究时，直壁体的堆敷成形采用了往复成形的熔敷方式，封闭路径在堆敷成形时将熄弧端放在起弧端的后面，两者之间的距离为8mm，保证能形成封闭路径，减小高度差。堆积的高度增加后，采用了补差的方法来保证成形。在解决电弧增材制造封闭路径成形问题上，现有的解决办法主要是采用补偿的方式，但在进行补偿时往往是基于工艺经验或高端仪器，不具有高效且低成本的普适性。

因此，本文针对封闭路径在电弧增材制造成形过程中出现的闭合处缺陷，提出了基于多元回归模型的过度补偿方法来解决起闭合处塌陷的问题，并准确计算过度补偿距离。该方法能够有效防止电弧增材制造封闭路径成形中出现的闭合处缺陷，且具有成本低、局限少、普适性高等优势。

2 试验方法

为获取电弧增材制造封闭路径成形过程中的焊接参数及成形件尺寸参数，设计了相应的试验计

划。以退态火Cr5钢为母材（150mm×100mm×15mm），其化学成分见表1。Cr5钢母材在堆焊前需要先去除表面氧化层、油污，用酒精进行清洗，并在120℃的鼓风干燥箱中进行2h干燥后待用。选用焊丝的牌号是ER308L，化学成分见表2。采用松下Panasonic YD-500GS电弧堆焊机进行试验，98%Ar+2%CO2混合气体作为保护气体。

表1 Cr5钢化学成分（质量分数） （%）

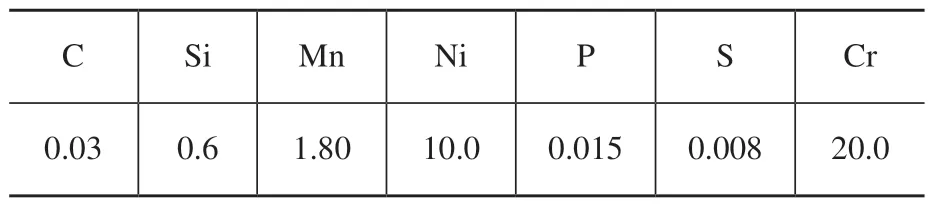
表2 ER308L主要化学成分（质量分数） （%）

3 封闭路径成形参数研究

3.1 封闭路径

根据弧坑塌陷长度确定补偿距离设计了试验方案，为了方便测量熄弧处塌陷的长度，设计的封闭路径为长60mm、宽25mm的长方形路径。先开展的试验是未采用补偿策略的长方形路径的成形试验，如图1所示。另外，对熄弧处塌陷的长度和余高与对称位置处焊缝的余高用游标卡尺进行了测量并记录，见表3。其中弧坑长度就是熄弧处塌陷的长度，高度差是指熄弧处余高与对称位置处余高的差值。

图1 未补偿的焊接结果及弧坑长度

3.2 焊接参数的回归分析

为有效计算过度补偿距离，采用回归分析探究焊接参数与弧坑长度之间的关系。本次回归分析中采用多元回归进行建模，焊接参数作为自变量，弧坑长度作为因变量，共选取27条样本量作为研究数据集，构造回归方程用于探索自变量与因变量之间的关系，建立多元回归模型用于计算有效的过度补偿距离。

在电弧增材制造过程中，根据回归分析的基本理论确定的变量之间的关系表达式为

式中y——弧坑长度（mm）；

x1——焊接电流（A）；

x2——焊接速度（m/min）；

x3——焊接电压（V）。

利用SPSS软件进行回归分析可以得出弧坑长度的常数项为5.507，焊接电流的系数为-0.001，焊接电压的系数为0.343，焊接速度的系数为-1.001。

弧坑长度的数学表达式为

式中L——弧坑长度（mm）；

I——焊接电流（A）；

U——焊接电压（V）；

S——焊接速度（m/min）。

图2所示为计算值和实际值的对比。从图2中可知，实际值和计算值之间的误差值是很小的，这说明上述回归方程表达式可以很好地解释焊接参数与熄弧处塌陷长度之间的关系，当焊接速度、电弧电压和焊接电流中任意一个发生变化时，弧坑长度都会随之发生变化。

图2 弧坑长度的计算值与实际值对比

4 补偿策略成形试验

4.1 补偿距离的确定

根据弧坑长度的回归方程表达式，可知弧坑长度随焊接参数而变化的规律，因此可以根据此规律进行补偿距离计算的研究。以未采用补偿策略的弧坑长度为依据，在此基础上对每一组焊接参数下的封闭路径进行多次过度补偿试验，即让焊枪在熄弧处往前多走一段距离，让熄弧端覆盖在起弧端的上面，如图3所示。同时测量记录在相应的焊接参数下，每一道闭环焊道的补偿距离及补偿高度差，见表4。

图3 补偿后的试验结果

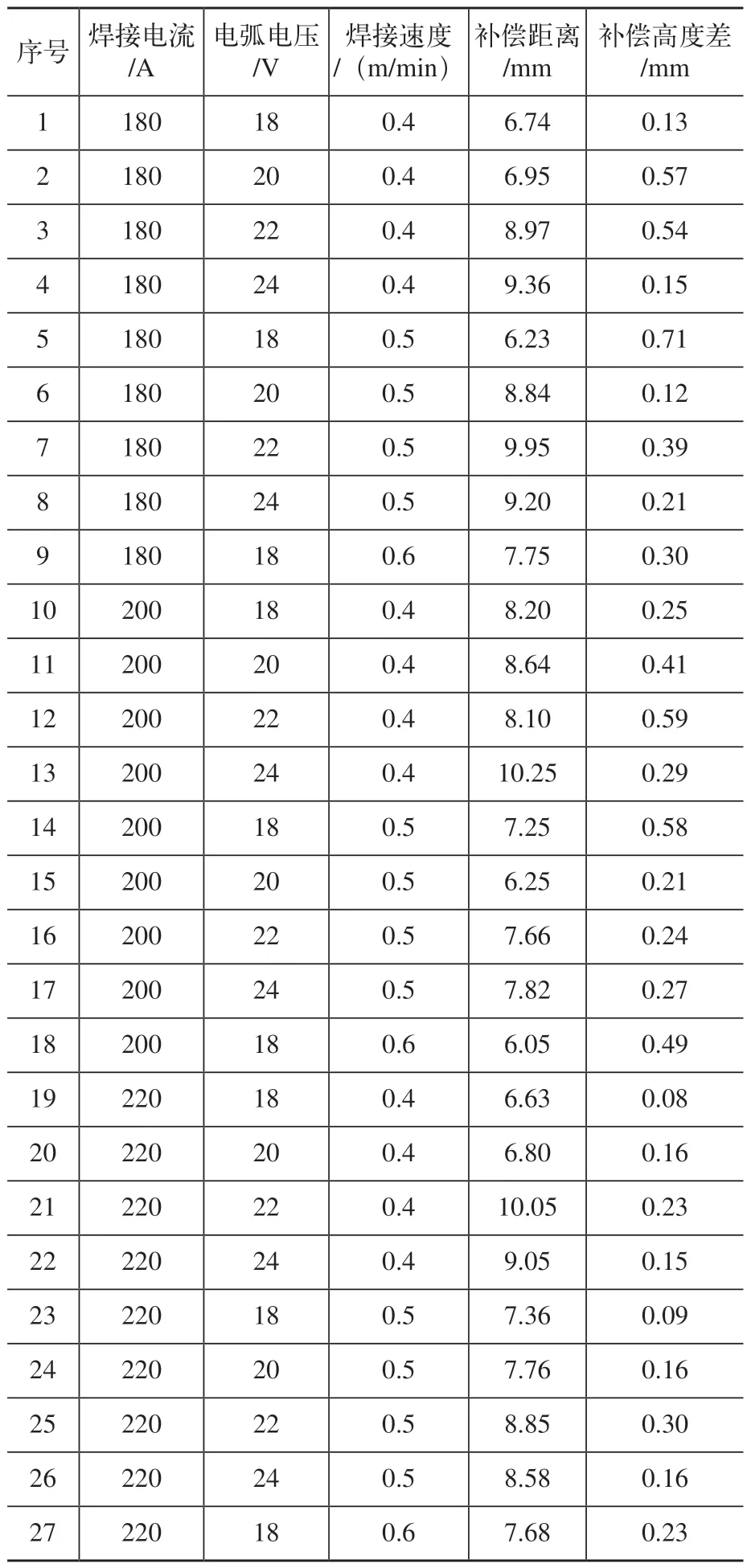
表4 补偿后的试验数据

从未采用补偿策略的焊接结果和采用补偿策略的焊接结果对比可以看出，采用补偿策略后，在起弧点和熄弧点闭合处塌陷的缺陷起弧端与熄弧端闭合处的塌陷缺陷得到了明显的改善。根据补偿前的高度差和补偿后的高度差两组数据，可以充分说明过度补偿策略解决封闭路径闭合处搭接不平的缺陷是可行的。

由表4可知，补偿后的高度差值均在1m m之内，在误差允许范围内，对最终成形件的影响很小，说明补偿时依据弧坑长度确定的过度补偿距离是合适的。为了表明补偿距离与弧坑长度之间的具体关系，对补偿距离和弧坑长度这两组数据进行了一元线性回归分析，将补偿距离作为因变量，弧坑长度作为自变量，并利用SPSS软件进行回归分析计算，得到了补偿距离的常数项为-3.931，弧坑长度的系数为0.997，因此两者之间的关系

式中I——补偿距离（mm）；

L——弧坑长度（mm）。

将测量后的弧坑长度数值代入上述关系式中，可以计算出补偿距离具体数值，然后将计算值与实际试验策略值进行对比，如图4所示。从图4可看出，两者数值几乎重合，误差均值接近于零。说明该关系式计算出的补偿距离合理。

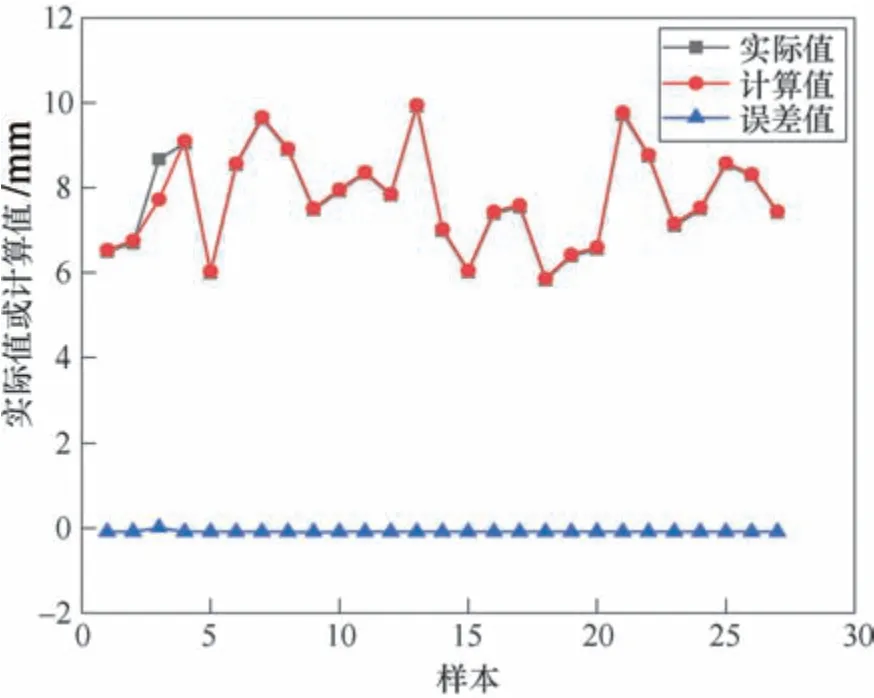
图4 过度补偿距离的计算值和实际值对比

在一定的焊接参数范围内，根据弧坑长度和补偿距离的关系式，可以对不同尺寸和形状的封闭路径进行补偿距离的计算，能够有效达到控制成形形貌的效果，避免了大量补偿距离的试验，从而提高了工作效率，节约了试验用材料。

4.2 圆形路径补偿策略验证试验

在进行圆柱薄壁结构堆积试验时，随着高度的增加，往往会出现明显的阶梯效应，很大程度影响了成形形貌，甚至有可能会出现焊枪碰撞事故，因此采用闭环路径补偿策略来减少阶梯效应的出现。用游标卡尺对未采用补偿策略的圆弧构件熄弧处塌陷长度进行了测量，测得熄弧处塌陷的长度为15.05mm，将测量得到的塌陷长度带入补偿距离的计算公式，得到的结果为11.07385mm，由于机器人系统的限制，因此在程序中设置的补偿距离为11.08mm，通过弧长计算公式将补偿距离转换成旋转角度，旋转角度为21°，在圆弧焊接程序中将机器人的旋转角度设定为360°+21°，采用补偿距离后的圆弧闭合构件成形效果如图5所示。

图5 圆弧补偿堆积结果

从图5可看出，焊枪旋转的总体角度>360°，圆弧闭合处成形良好，无明显的塌陷缺陷。对搭接位置处的高度与对称位置处的高度进行测量对比，两者的高度差值为0.66mm，对最终成形质量影响很小。该试验说明了过度补偿距离的计算公式可以用于圆弧补偿距离的计算。

由于采用补偿策略后圆弧成形形貌良好，在此基础上进行直径为60m m的圆柱薄壁件堆积成形。根据上述补偿策略公式计算结果，在焊接过程中每一层在成形时焊枪都会在闭合处往前多走11.08mm，也就是让焊枪从起始点开始旋转，旋转方向为逆时针方向，旋转角度为360°+21°，每焊完一层，用测温计测量温度，温度降低至150℃时开始下一层焊接，直到焊接结束。圆柱薄壁件如图6所示，从图6中可看出，采用补偿策略后，圆柱薄壁件在搭接处成形良好，没有明显的阶梯效应出现，能形成平整的封闭特征。在圆柱薄壁件上取8个位置（见图7）测量其高度，将测量得到的高度值利用绘图软件绘制成点线图（见图8），这8个位置的高度差值均在1mm左右，对成形件影响很小，这充分说明了确定的补偿距离在实体件成形过程中也是可行的，能够解决熄弧塌陷问题。

图6 圆柱薄壁件成形示意

图7 圆柱薄壁件高度测量

图8 圆柱薄壁件高度测量结果

5 结束语

1）针对电弧增材制造封闭路径在电弧成形时闭合处会出现阶梯效应的塌陷问题，采用了基于多元回归分析模型的过度补偿策略解决，并给出了回归方程计算的具体流程，适用于封闭路径规划下的电弧增材制造，能够计算出封闭路径成形件闭合处的塌陷弧坑补偿距离，并使用计算值与试验值的误差计算进行了证明。

2）选用圆柱形薄壁结构进行电弧增材制造试验，并应用回归方程对其进行了补偿策略的距离计算，通过对圆柱形薄壁结构的电弧增材制造试验，规划和试验结果表明，所提出的补偿策略精度较高、普适性强。