考虑阻抗比影响的三维沉积盆地地震动时-频放大特征

2023-08-18吴烨钦于彦彦丁海平

世界地震工程 2023年3期

吴烨钦,于彦彦,丁海平

(苏州科技大学江苏省结构工程重点实验室,江苏苏州 215009)

0 引言

国内外多次大地震的震害经验和相关研究表明:沉积盆地对其内部的地震动有显著的放大效应,进而导致盆地内的震害更加严重。盆地对于地震动的放大作用已被大量的观测记录、震害调查及数值模拟结果所证实[1-6]。研究表明:沉积盆地的边缘效应、聚焦效应和共振效应等会导致盆地内局部或整体地震动放大,地面运动持续时间显著延长。

在盆地地震效应的研究方法中,数值模拟方法以其简便、高效、可考察整个盆地范围等优点而成为主要手段[7-12]。相较其他模拟方法,谱元法兼具有限元法的几何适应性好以及伪谱法的高精度、低频散的优势,因此得以广泛应用。于彦彦[13]采用谱元方法结合并行计算技术,研究了真实三维盆地在设定或真实地震作用下的响应特征,分析了地震波在盆地内的传播过程、盆地内的地震动分布以及面波的形成与传播;PILZ等[14]基于谱元法模拟了智利盆地在地震破裂下的地面运动放大特征;JAYALAKSHMI等[15]利用谱元法模拟了潜在大地震作用下印度-恒河盆地的三维地震波放大效应。

需指出的是:以上三维盆地地震效应模拟研究多针对特定震源下特定盆地的地震响应,以预测或解释盆地内的强烈地震动,重点集中于盆地对地震动的影响之上,而对于介质参数引起的阻抗比差异对盆地放大效应的影响关注不多。刘中宪等[16]基于谱元法和动力学震源模型研究了盆地内外介质的波速比对地表地震动时程和峰值的影响;李雪强[17]和强生银[18]建立了一系列具有不同介质阻抗比的理想盆地模型,详细研究了平面波入射下盆地内外介质阻抗比对盆地内地震动及面波强度的影响。这些研究均表明盆地内外介质阻抗比对地震放大作用有较显著影响。不同的介质阻抗比会影响地震动的强度,产生的地震动分布情况可能完全不同。但以往的阻抗比影响研究大多针对二维盆地模型,有必要开展阻抗比对三维沉积盆地地震效应影响的研究。

本文拟基于设定盆地和震源模型,采用谱元法模拟不同阻抗比下三维沉积盆地的地表地震动[19],通过分析不同阻抗比模型的地面峰值速度(PGV)及时域和频域放大系数的分布,研究阻抗比对三维盆地在时域和频域内的地震动放大效应的影响。

1 计算模型与计算方法

建立如图1所示的计算模型,模型尺寸为27 km×9.3 km×15 km,盆地形状为三维梯形。网格划分时对盆地-基岩分界面进行了精确构建,即采用标准倾斜平面构建介质分界面,在此基础上进行单元划分。盆地长宽分别为6 km和2 km,斜面倾角为45°,盆地深度为200 m。取矩震级为 5级的点震源(图1中黑色圆点所示),其位置坐标为(-11, 0, -12)km,震源倾角90°,滑动角和走向均为0°。震源参数基于经验统计公式确定[20]:地震矩为3.548×1016N·m,上升时间为0.14 s。震源时间函数如图2所示。

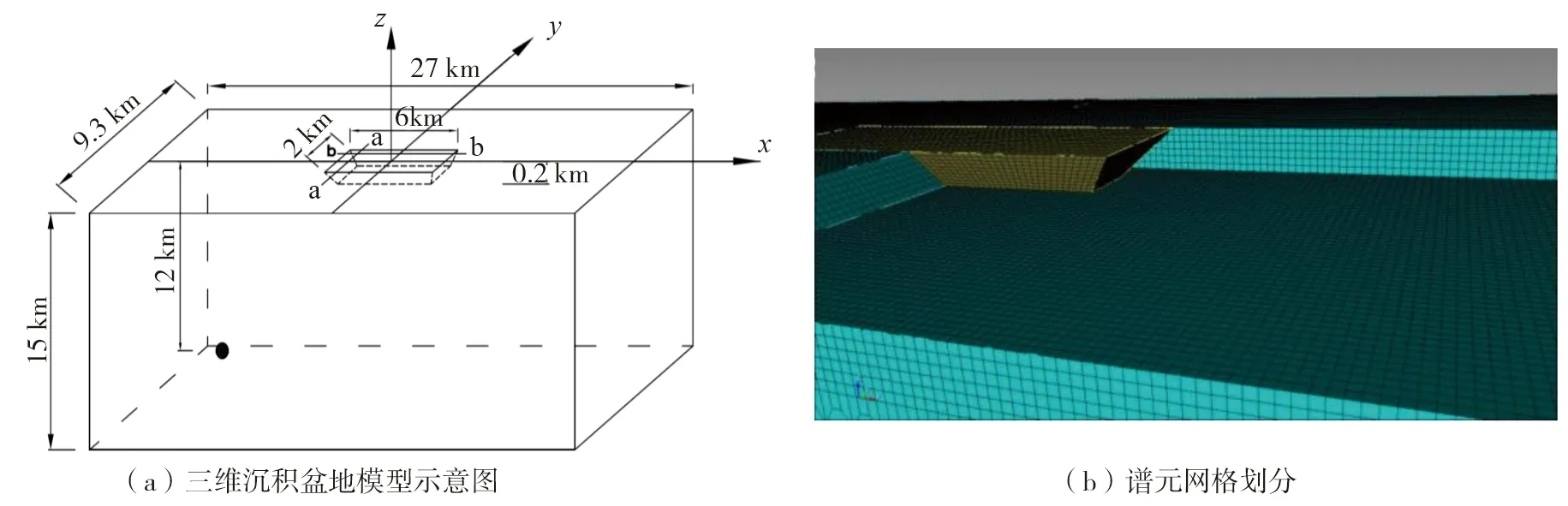
图1 三维沉积盆地模型示意图及谱元网格划分Fig. 1 Schematic diagram of 3D sedimentary basin model and spectral element meshing

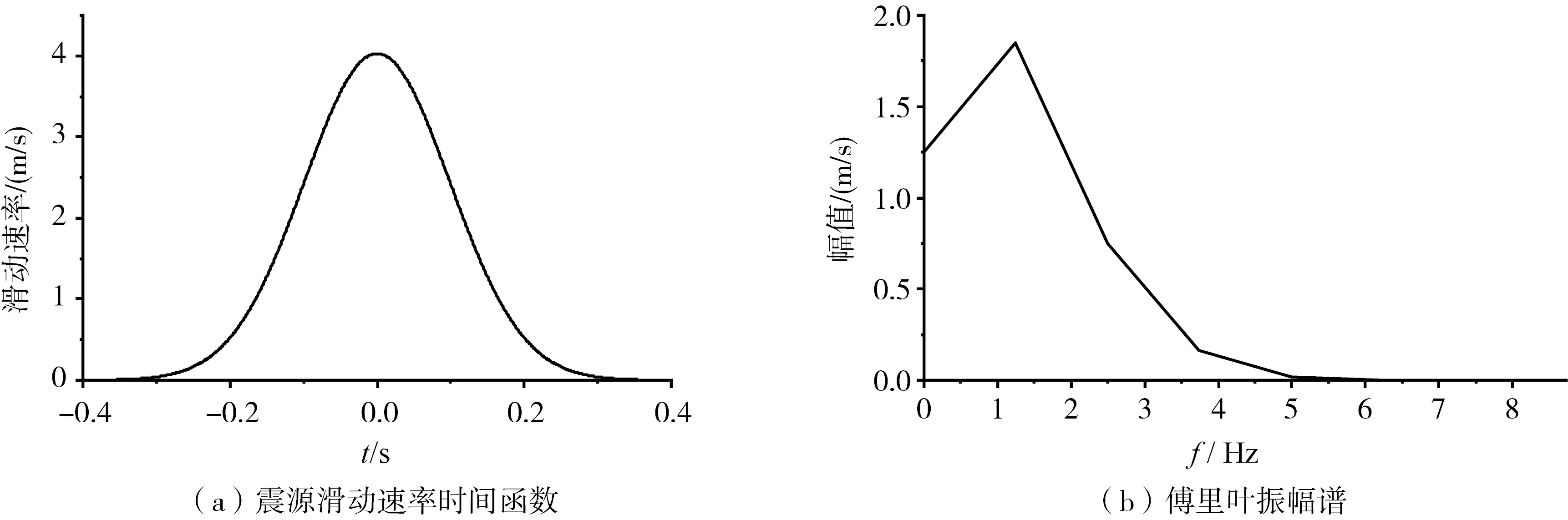
图2 震源滑动速率时间函数及其傅里叶振幅谱Fig. 2 Time function of the source sliding rateand its Fourier amplitude spectrum

图3 剖面a-a 的EW(左)、NS(中)和UD(右)分量的速度时程Fig. 3 Velocity time histories of EW, NS and UD components of profile a-a

图4 剖面b-b 的EW(左)、NS(中)和UD(右)分量的速度时程Fig. 4 Velocity time histories of EW, NS and UD components of profile b-b

在盆地内和外地表处共布置2442个观测点,其中盆地内每隔100m布置一个观测点,共1342个测点;盆地外每隔500m布置一个观测点,共1100个测点。

为了分析阻抗比对三维沉积盆地地震动的影响,本文考虑了6组不同的阻抗比模型,盆地覆盖层及其外部基岩介质的参数列于表1。其中仅改变盆地内土层的剪切波速,盆地外基岩的波速和密度恒定为:Vp=4330 m/s,Vs=2 500 m/s,ρ=2 500 kg/m3。盆地内土层的密度恒定为1 700 kg/m3,介质剪切波的品质因子Qs由经验公式Qs=Vs/10确定[21],其中:Vs为介质剪切波速。表中:f0为根据盆地介质剪切波速及盆地的最大深度(200 m)算得的盆地最深处土层的一维自振频率。

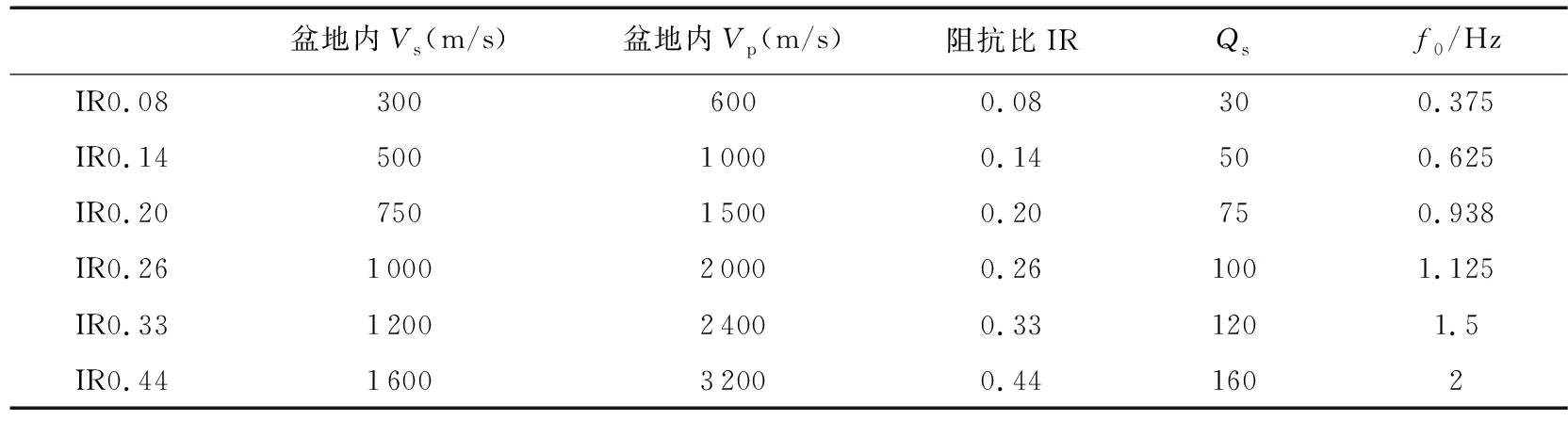
表1 不同阻抗比模型的介质参数Table 1 Numerical simulation parameters of ground shaking in the basin model

本文采用四阶谱元法模拟三维沉积盆地的地震动,插值函数采用 Lagrange 多项式,单元节点,即插值点,取为 Gauss-Lobatto-Legendre 积分点(GLL 点)[13]。为了保证模拟精度,确定网格时须满足以下条件:1)一个最短波长内至少包含一个网格单元。2)观测点到震源之间必须包含两个或两个以上的网格单元[22]。因此盆地内部平均网格尺寸为100 m,基岩最大网格为300 m。计算模型单元463140个,时间步长为0.0003 s,模拟时长为30 s。

2 结果分析

2.1 不同阻抗比下三维沉积盆地的剖面时程

选取横穿盆地长和短边的剖面b-b和a-a(位置见图1)的速度时程分析不同阻抗比下的波动传播特征。图3-4分别为剖面a-a和b-b的三分量的速度时程。图中同时给出了对应剖面的沉积层厚度以及PGV的分布。

从剖面a-a的速度时程来看:三分量时程中都可见明显的盆地次生面波震相,且S波转换的次生面波(8s左右)强度显著大于直达P波引起的面波(5s左右)强度。此外,面波强度总体上随阻抗比的增大而减小。随盆地内外阻抗比的增大,波场由复杂变得相对简单。这是由于阻抗比较小时,盆地内次生面波较为发育[13],同时入射到盆地内的体波及盆地边缘的次生面波在松软的沉积层内衰减缓慢,并在盆地-基岩分界面发生多次反射,不同波型的叠加干涉导致波场更为复杂。对EW分量,各阻抗比下均有明显的盆地边缘效应,同时IR0.08到IR0.44对应的盆地中心区域的地震动强度也始终较大。对NS分量,如前所述,由于震源辐射方式的影响,盆地中心点在该分量的直达体波的地震动幅值基本为0,但阻抗比小于0.2的模型在该区域处均表现出较强烈地震动,其中:IR=0.14模型在该位置处由于地震波的叠加干涉而出现局部的强地震动区,反映出三维盆地效应的影响。比较而言,垂直分量的地震动时程最为复杂,地震动强度整体随阻抗比增大而衰减。

剖面b-b横穿盆地长边,其地震动主要受邻近的盆地边缘地震动的影响。在4 s和7 s以后P波和S波分别抵达盆地左侧边缘,在盆地边缘衍生出相对复杂的面波,面波与体波的叠加干涉显著放大了该区域的地震动。体波从左至右抵达盆地,因此时程图中可见按恒定时差倾斜排列的体波震相。同时,可以看出S波在传播过程中的衰减作用相比P波强烈。当体波到达盆地右侧边缘后,同样有次生面波出现并向盆地内传播,但在小阻抗比模型下,由于更强的品质因子,其传播距离相对更短。

2.2 不同阻抗比下三维沉积盆地地表峰值速度和放大系数分布特征

基于上述盆地模型模拟得到的点源作用下地表峰值速度(PGV)的分布如图5所示,其中:图5(a)～图5(f)为IR0.08至IR0.44对应的结果(下同)。图中最外侧线为盆地范围,白色框线所示为盆地基底的地表投影。

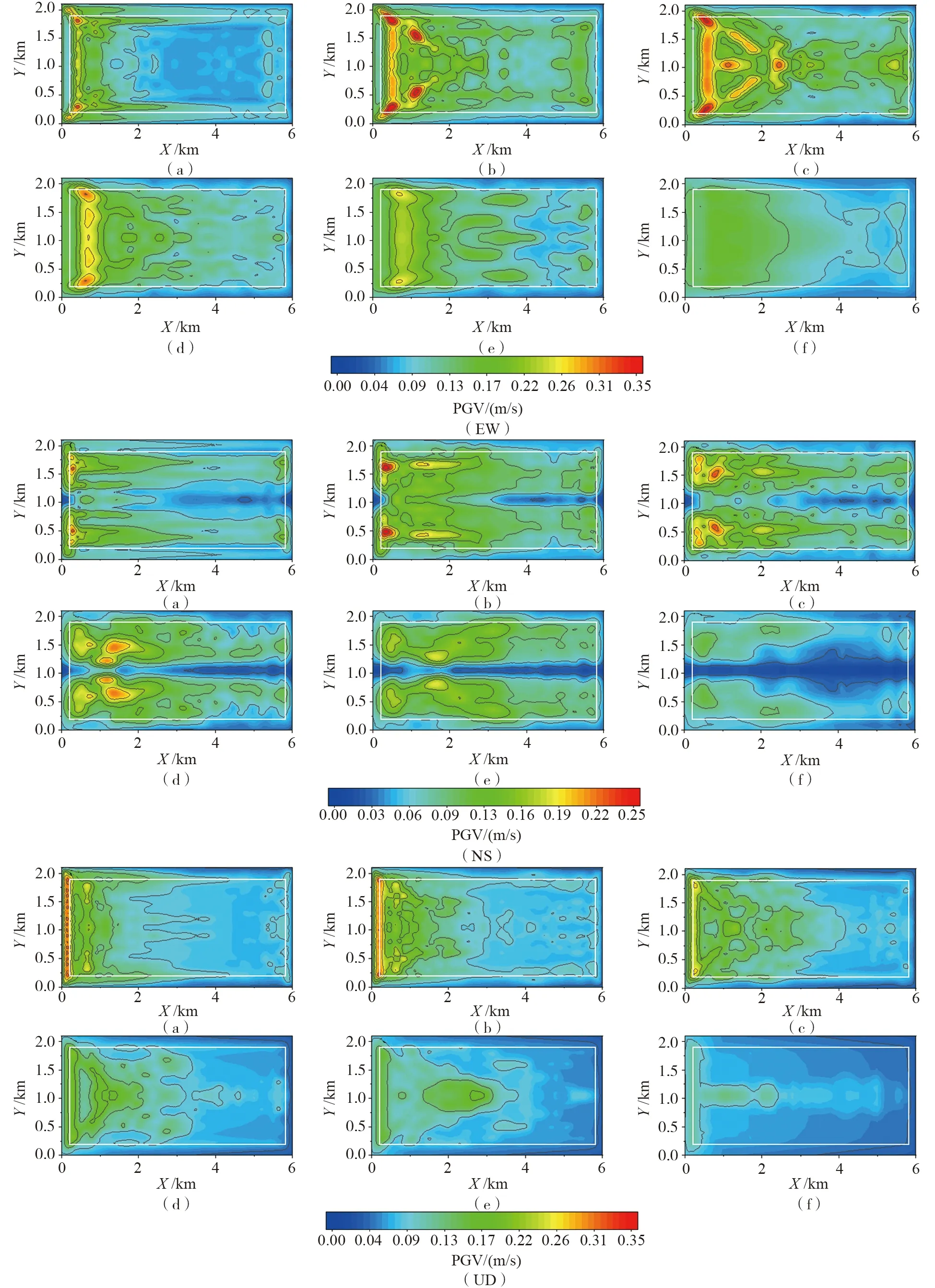
图5 不同阻抗比模型下EW、NS和UD分量的PGV分布Fig. 5 PGV distributions of EW, NS and UD components for different impedance ratio models

对比图5中EW分量的结果可以看出:阻抗比IR=0.08时,盆地模型左侧边缘区域的速度峰值明显大于其他区域,并且紧靠基底地表迹线的内侧。在左侧两个角点处的地震动最为强烈,其处于两斜边的交界位置,受到体波和面波多次叠加,因此在数值上明显高于其他区域。当阻抗比由0.08增加到0.14时,盆地边缘区域的速度峰值急剧增大,并且在角点向盆地中心区域延伸线上速度峰值也非常显著。随着阻抗比继续增大,速度峰值较大区域向盆地中心位置继续发育,但IR大于0.2以后最强烈地震动又集中在盆地左侧边缘区域,且速度峰值的最大值随IR增大逐渐减小。此外,从图中可以看出随着阻抗比的增加,盆地边缘速度峰值较大区域逐渐向盆地中心移动。

从图5中NS分量的结果来看:其速度峰值较大区域在盆地上下两侧呈带状分布。阻抗比IR=0.08时,盆地左侧边界处的速度峰值也明显高于盆地其他区域;当阻抗比由0.08增加到0.14时,地表地震动幅值增大为所有阻抗比模型中的最大值,速度峰值较大区域在靠近上下两侧基底迹线附近出现,这与EW分量不同。随着阻抗比的继续增大,地表速度峰值减小,且速度峰值较大区域向前移动并逐渐靠近盆地长边中轴线。

对于垂直分量图5中(UD),在阻抗比IR=0.08时,速度峰值强烈区域集中在盆地左侧边缘及基底地表迹线外侧。当阻抗比增大但小于0.2时,地震动最强烈区域整体向盆地内部略微移动,但总体集中在盆地左侧边缘至盆地基底短边迹线附近。随阻抗比的进一步增大,最强烈地震动转移至盆地中心区域。垂直分量的速度峰值最大值出现于阻抗比IR=0.14的模型,达到了0.38,随IR增大,该分量地震动峰值减小。此外,无论是水平分量还是垂直分量,都存在阻抗比较小时盆地内部的速度峰值分布较复杂的现象。

根据一维成层介质波动理论,地震波由硬介质(基岩)传播至软介质(土层)时,透射波的幅值E′满足以下关系[23]:

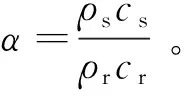
显然,由于土层相比基岩软弱,因此α<1,故E′>E,即波由基岩进入土层时幅值会变大。且随α增大,E′的值会相应减小。这可在一定程度上解释地震动幅值随阻抗比增大而减小的原因。但对于三维盆地模型,其盆地内部还存在有次生面波,面波与直达波或多次反射波的叠加干涉使得阻抗比对三维盆地内地震动幅值的影响规律更加复杂。

巴振宁等[24]研究了逆断层作用下三维半椭球沉积盆地的地震动,发现沉积内外介质波速比对盆地竖直向地震动的影响显著,介质波速比降低时,盆地内部地表峰值增大。本文垂直分量的结果与之一致。但考虑本文的盆地形状、断层形式及研究的阻抗比范围的不同,水平分量的地震动峰值并非随阻抗比的减小而单调增加,如对于本文模型,水平分量上均是IR=0.14时的速度峰值最大。

为进一步研究盆地内外阻抗比对盆地地震动放大效应的影响,采用基岩均匀半空间模型为参考模型,并定义放大系数为盆地模型与半空间模型地表峰值速度之比。图6给出了不同阻抗比下,计算模型EW、NS和UD三个分量的放大系数分布。

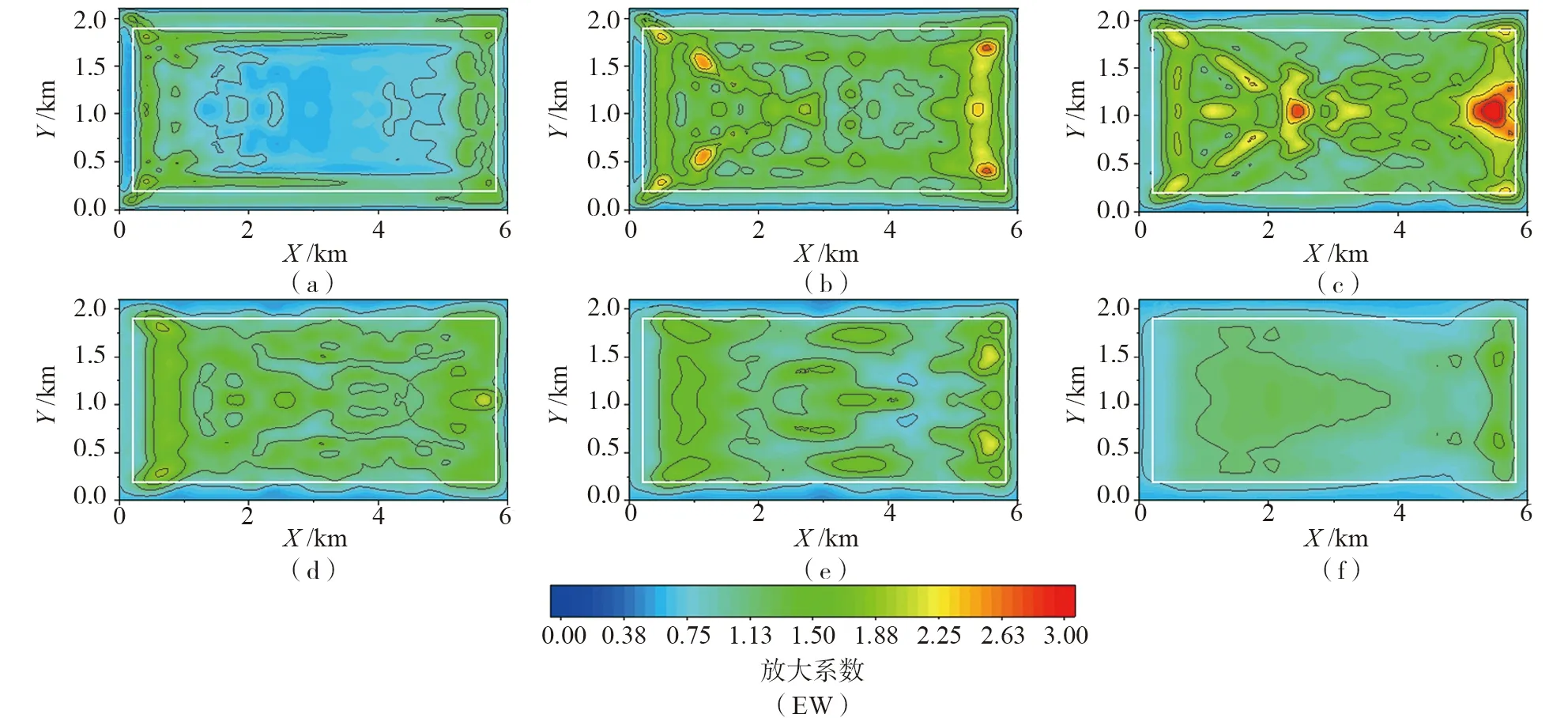
图6 不同阻抗比模型下EW、NS、UD分量的放大系数分布Fig. 6 Distribution of the amplification coefficients of EW, NS and UD components for different impedance ratio models

分析图6中EW分量的放大系数分布,放大系数的最大值达到了3.0左右,可以看出放大效应强烈区域与PGV分布图中速度峰值较大区域基本一致,不同的是盆地右侧区域也出现了放大效应强烈的区域(并可能是放大系数最大的区域),且随着阻抗比的增大从右侧上下角点区域向右侧中心区域汇聚。

图6中NS分量的放大效应强烈区域位于盆地长边中线处,呈现一狭长区域。同时,相比其它两分量,NS分量的放大倍数相对要大得多。考虑采用的震源模型的辐射方式(基岩半空间模型在盆地长边中线处的地震动值基本为0),这一放大效应归结于盆地的存在,或三维盆地效应导致的长边中线处的明显地震动。对于UD分量,其放大系数最大值达到了3.68,且放大系数的分布与PGV的分布也较为一致。此外,除IR=0.44的模型外,其余阻抗比下的放大系数均较大。

2.3 不同阻抗比下三维沉积盆地频域放大系数分布特征

图7-9给出了阻抗比变化时,沉积盆地内部在0.5 Hz、1.0 Hz和1.5 Hz三个特征频率处的频域放大系数分布,即地表观测点与均匀半空间对应观测点在以上特征频率处的时程谱比值。

可以看出:对EW分量(图7),在0.5 Hz时,盆地的放大效应在阻抗比IR=0.08时为最大(6.34),位于盆地左侧边缘区域,随阻抗比的增大,盆地内的放大效应迅速减小,当阻抗比大于0.2时,盆地内的放大作用已十分不明显;在1.0 Hz时,盆地内的放大效应在阻抗比IR=0.14和0.2时为最大,而阻抗比IR=0.08对应的盆地放大效应有所减弱,当IR大于0.2时放大系数逐渐减小;1.5 Hz时,盆地放大效应最大值出现于阻抗比IR=0.26所对应的盆地模型。随阻抗比的减小或增大,放大系数都相应减小。

图8给出了NS分量的结果。盆地的放大效应在0.5 Hz和1.0 Hz时分别在阻抗比IR=0.08与IR=0.14时达到最大值,分别为5.06与7.1。对于大多数情况,NS分量的放大效应位于盆地上下两侧区域,在短边中线附近的狭长的区域内,其放大效应相比盆地其他位置要小很多。但1.5 Hz下IR=0.33的结果(图e)除外,其放大系数整体上显著大于其他阻抗比的情况,结合盆地中心土层的自振频率推测该频率等于盆地自振频率,因此地震动被强烈放大,导致其在整个盆地内的显著放大效应。

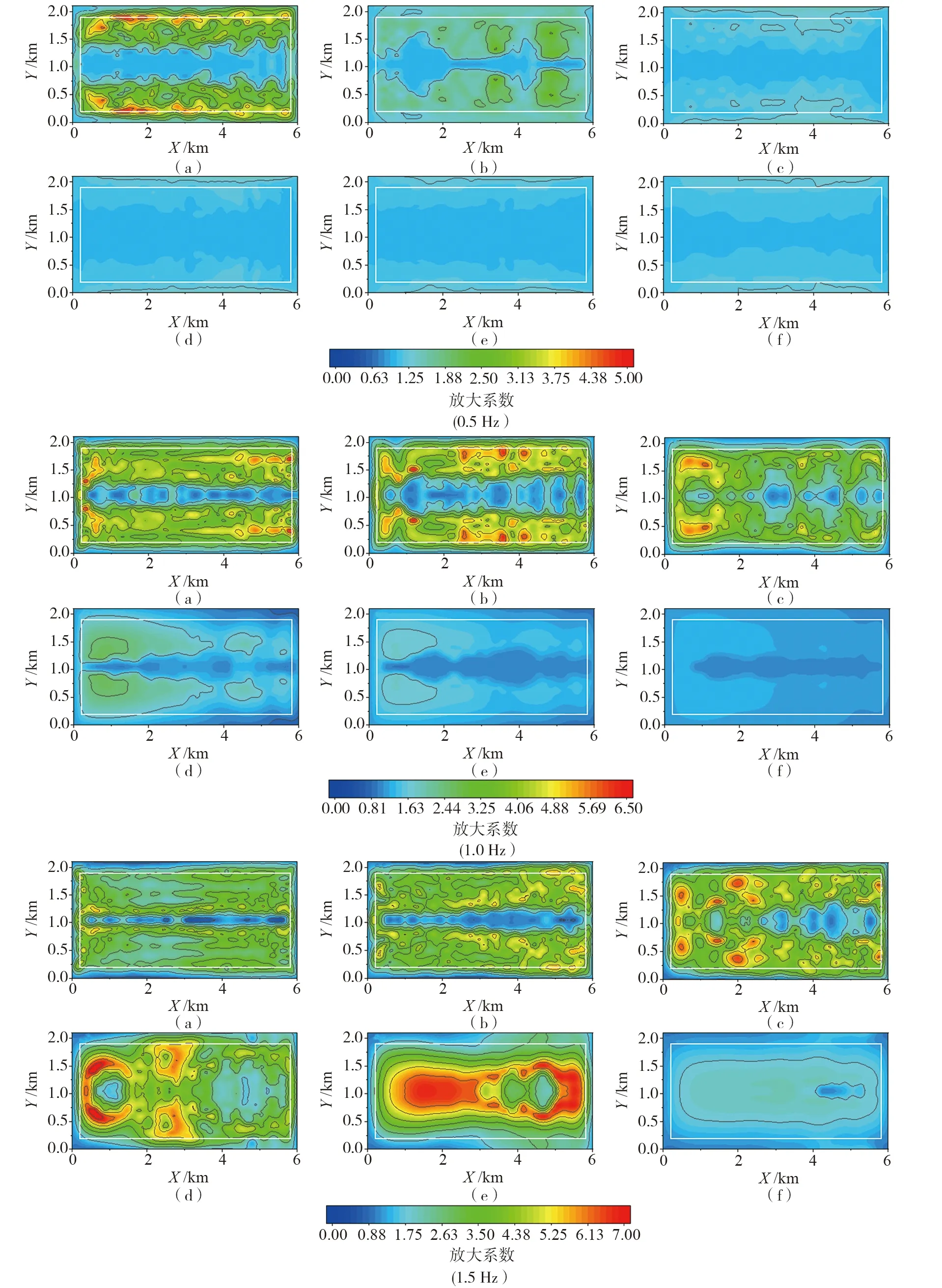
图8 不同阻抗比模型下NS分量的频域放大系数分布Fig. 8 Distribution of frequency domain amplification coefficients of NS components for different impedance ratio models

观察图9中UD分量的结果,垂直分量在不同阻抗比下的最大放大系数对应的频率仍与盆地的一维自振频率有一定关系,如0.5 Hz时IR=0.08模型对应的放大系数最大,但这一相关性相比两个水平分量要低得多;如1.5 Hz时在NS分量上出现的显著放大效应此时并未出现,最强烈放大效应出现于IR=0.14模型。此外,不同频率下放大系数的分布特征也与水平分量显著不同,比如0.5 Hz时IR=0.08模型的最大放大系数出现于盆地右侧区域。

以上结果表明:同一阻抗比下,不同频率的某分量地震动具有不同的放大倍数,这与WEN等[2,25]基于台北盆地的观测记录,采用谱比法对盆地效应的研究结论一致;MOCZO等[26]的研究表明:盆地-基岩的波阻抗差异越大,时域内盆地地震动的放大作用越强烈;MEZA-FAJARDO等[27]指出盆地内地震动最大放大系数还随盆地形状和频率而改变,但其针对的是半椭球形盆地和平面波入射的情况。本文基于三维梯形盆地的结果(图7-9)与以上研究结论总体一致,尤其是对于0.5Hz的长周期地震动,但放大系数分布更加复杂。本文结果还表明阻抗比同时影响频域放大系数的分布及特定频率下最强烈放大系数的位置。